基于分子动力学的纳米水滴粘度及接触角计算

尹宗军，苏 蓉，王清清，梅媛春，李 永

安徽信息工程学院机械工程学院，安徽芜湖,241100

液滴撞击壁面的运动机制广泛应用于各类技术，如降膜蒸发、喷墨打印、农药喷洒以及燃油喷射撞壁等[1]。通常把气-固-液的交界面称为三相接触线，移动接触线具有跨尺度关联性质，其在连续介质框架下的力学奇异性(或称为Huh-Scriven佯谬)一直是界面润湿动力学的核心力学问题。尽管一些消除该力学奇异性的机制被相继提出，例如前驱膜、滑移边界以及扩散界面等很好地消除了移动接触线剪切应力的r-1奇异性。然而，纳微系统和宏观系统服从不同的物理规律。在纳微米尺度上，比表面积将导致某些力学量具有微尺度效应[2]。随着微纳米技术的发展，对纳微液滴在固体界面的变形与流动的微观细节日益突出，故有必要在纳微尺度上研究分子团簇的流变行为演化。

近年来，利用CFD(Computational Fluid Dynamics)或者相场动力学方法研究宏观液滴界面拓扑行为引起了研究者的持续关注，例如VOF(Volume of Fluid)、Level Set以及CLS-VOF(Couple Level Set & Volume of Fluid)等。李燕[3]运用VOF模型对液滴撞击后变形过程的流场、压力场的变化进行数值模拟。Lunkad等[4]亦采用VOF模型，研究静态接触角(SCA)和动态接触角(DCA)模型对液滴撞击水平壁面和倾斜壁面的铺展行为的区别。采用无量纲方法研究不同机制下液滴沉积、反弹以及破碎等变形模式，从而得到具有普适性的结果或变形模式转变的判据。液滴撞击壁面过程的力学相似准则主要由下面几个无量纲数描述[5-6]：

(1)

式中,ρ表示液滴密度，g为重力加速度，μ为动力粘度，D0表示液滴直径，V0表示液滴初始撞击速度，γ表示液滴表面张力。Re为雷洛数，是惯性力与粘性力的比值；We为韦伯数，是惯性力与表面张力的比值；Oh为奥内佐格数，是黏性力与惯性力和表面张力的相互关系的无量纲数。

Rioboo等[7]引用铺展因子β=D/D0(D为铺展直径)随无量纲时间t*=tV0/D0的变化特性将液滴撞击干壁面分为运动、铺展、弛豫和湿润四个阶段，着重讨论撞击速度、液滴直径、黏度、表面张力以及壁面粗糙度等对铺展特性的影响。在液滴撞击壁面过程中，基于唯象理论的流体力学控制方程满足能量守恒定律，其主要包含动能、表面能、粘性耗散能、重力势能,甚至仍需要考虑液滴与壁面接触的粘附力做功。在已有的研究中，通常忽略重力势能，也不考虑粘附力作用的影响。Yarin[1]曾形象地比喻惯性力、表面张力以及粘性力是液滴流动演化的雕刻家。Chandra等[8]根据动能、表面能及粘性耗散能三者之间的能量守恒关系计算出射流阶段最大铺展因子βCmax满足方程：

(2)

其中,θS为静态接触角。Pasandideh-Fard等[9]改进了粘性耗散函数y方向上的特征长度，得到更为精确地预测βFmax的关系式：

(3)

很显然当Re→∞时，两者是等价的。Moita等[10]认为从液滴刚接触壁面到铺展因子达到最大时，对应的无量纲时间是一个常值，铺展因子β(t)与βmax满足下式：

(4)

因此，当t*=3/8时，铺展因子达到最大。Mundo通过实验观测了液滴在不同条件下产生的变形特征，引入Sommerfeld数K=Oh·Re1.25作为判定液滴碰撞发生反弹、沉积及飞溅的判据。此外，袁泉子等[11]详细讨论了移动接触线自相似扩展的标度关系，即D～tn，n为幂指数并与壁面和能量耗散有关。

事实上，对介观、宏观液滴做了大量细致研究的同时，但对纳微液滴的润湿动力学的研究工作并不多见。对宏观液滴撞击的研究结论在纳米尺度是否仍然适用尚不清楚，如何把纳微米尺度上力学行为表征出来仍具有许多棘手的细节问题。受时空限制，纳米液滴撞击壁面的实验研究虽难开展，但采用MD(Molecular Dynamics)方法却可以提供原子、分子的运动行为细节及其性态演化的全过程，其已然成为研究纳微体系必不可少的工具。Sedighi等[12]研究了纳尺度单氩液滴在固体表面润湿过程的分子动力学模拟，液滴撞击完全湿润壁、部分湿润壁以及不湿润壁分别出现了沉积、回缩以及反弹现象。Koishi等[13]进行了纳水滴撞击碳平板及纳柱表面的反弹研究，当纳柱高度增加时，跳跃和非弹跳状态之间的临界线向疏水性区域转移。清华大学陈民[14]开展了纳尺度水滴在铂表面润湿过程的分子动力学模拟，结果表明纳水滴存在两种破碎模式：水滴内部失稳破碎，表现形式为中心内陷并形成液环状；水滴边界失稳破碎，表现形式为指形溅射。另外，根据动能、表面能及粘性耗散能三者之间的能量守恒关系计算出射流阶段最大铺展因子βmax以及纳液滴破碎的Re-Oh无量纲判别式，分别为：

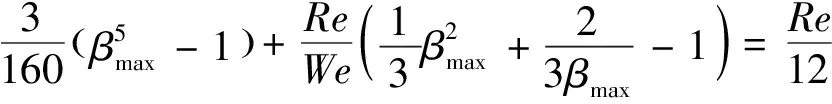
(5)

Oh·Re1/2=3.254

(6)

王宝和等[15]模拟了光滑壁面及其不同形貌的粗糙壁面上纳米水滴的润湿行为，并研究了固着纳米液滴的接触角滞后现象。Khan等[16]利用分子动力学研究在不同柱高和表面分数的纹理表面上纳米液滴从Wenzel态到Cassie态的转变行为。Niu等[17]研究了具有柱状结构的固体表面水滴的静态行为，其结果表明液滴处于Wenzel态或者Cassie态取决于柱状阵列的高度及其分布。Gao等[18]研究不同柱状结构参数的基底上水滴的动态润湿行为和水分子的凝结过程。

从前述可见，对纳米流体的润湿特性(标度律分析)和主动调控机制(包括移动接触线调控、蒸发与纳米颗粒沉积形貌调控以及壁面曲率诱发液滴自发定向运动操控等)有了一定认识，但对纳米液滴撞击行为动态演化过程还未有明确的研究，尤其是水的基本物理属性测试。本研究测试SPC(simple point charge)、SPC/E(extended simple point charge)、TIP3P(transferable interatomic potential with three points)以及TIP4P(transferable interatomic potential with four points)四种水分子模型的剪切粘度。然后选择纳米水滴撞击固体铜壁面作为研究载体，采用分子动力学方法模拟纳液滴撞击壁面过程，分析了纳米水滴低速撞击的运动形态特征，着重计算了其接触角。

1 仿真模型与参数设置

分子动力学仿真系统包括一个Lx×Ly×Lz的长方形盒子，其中Lx=150 Å，Ly=150 Å，Lz=200 Å。如图1所示，该盒子包括一个单纳米液滴和其下部的基底组成。整个仿真系统采用周期性边界条件，基板的尺寸大小满足液滴铺展过程中液滴前缘分子不跑出基底，并留有一定真空层。选择单纳米液滴的直径D0为80 Å，并让其位于体系坐标的原点。基板的材质选为铜Cu，设置为3个晶格长度，并让其位于纳米液滴以下15 Å。纳米液滴初始位置采用bcc晶格建模，晶格常数选择为a=3.915 Å，其值依赖于水分子的密度ρ=0.997 g/cm3。这并不意味着水具有固相特征，其仅仅作为建模方法可以有效地避免过大的初始势能。另外，基底Cu的晶格常数为b=3.615Å，采用fcc晶格建模。在T=303 K的温度下，水分子的初始平衡速度使用高斯分布随机产生，并满足Maxwell-Boltzmann速率分布律：

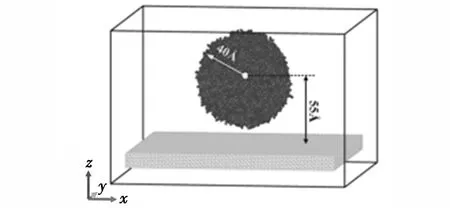
图1 纳米水滴撞击平坦铜壁面的初始构型图

(7)

其中,α=x、y、z,vα是速度v在α方向上的分量，m为每个原子的质量，kB为Boltzmann常数，T是温度。为了仿真纳液滴撞击过程，在z轴的反方向给液滴施加不同的撞击速度，初步假定为V0=0.003 Å/fs。针对Cu与水分子之间的相互作用，由于氢原子作用可忽略不计，用Cu-O原子间的交互作用来近似代替Cu与TIP4P的相互作用ULJ(r)，并采用Lennard-Jones 12-6势函数来定量描述：

(8)

其中,εCu-TIP4P为势阱深度，σCu-TIP4P为相互作用平衡时的特征长度。采用Lorentz-Berthelot混合规则估算Cu-O的交互作用参数，即用算术平均算Cu-O势阱深度、几何平均计算Cu-O平衡特征长度：

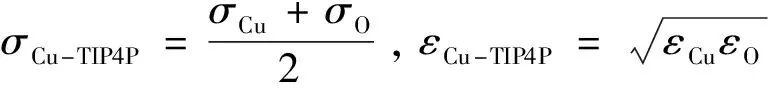
(9)

σCu=0.238 05 kcal/mol，εCu=2.340 Å，σO以及εO见表1。在这里，σCu和εCu是指Cu-Cu相互作用的LJ势参数，σO和εO是指O-O相互作用的LJ势参数。在计算过程中，设置LJ势的截断半径为12 Å，在K空间中采用PPPM求解器计算水分子内部间电荷相互作用的长程部分,并指定其实空间的截断半径为10 Å。在模拟过程中使用SHAKE算法固定H-O键的键长以及H-O-H的键角。一些水分子模型的参数值都被列在表1中，其中单位选用LAMMPS模拟软件中的real单位制[19]。计算过程中，原子位置与速度的更新采用为微正则系综NVE(N是总原子数，V是体积，E是能量)，撞击过程中不进行控温控压。注意仿真过程中移除了水对Cu基底的作用力，Cu基底固定不动。由于采用了限制动力学SHAKE算法限制水分子模型的健长和健角，因此时间步Δt被设置为1 fs。注意，基底的大小和水分子数要视仿真要求的不同而有所增减。为了避免体系能量过大导致模拟过程出现错误，在执行液滴撞击之前，整个体系须执行能量最小化，液滴单独使用Langevin热浴法进行驰豫500 ps。本研究所有的计算均在戴尔(DELL)Precision T5820/P5820X图形工作站上运行，电脑主机为至强W-21 333.6 Ghz。

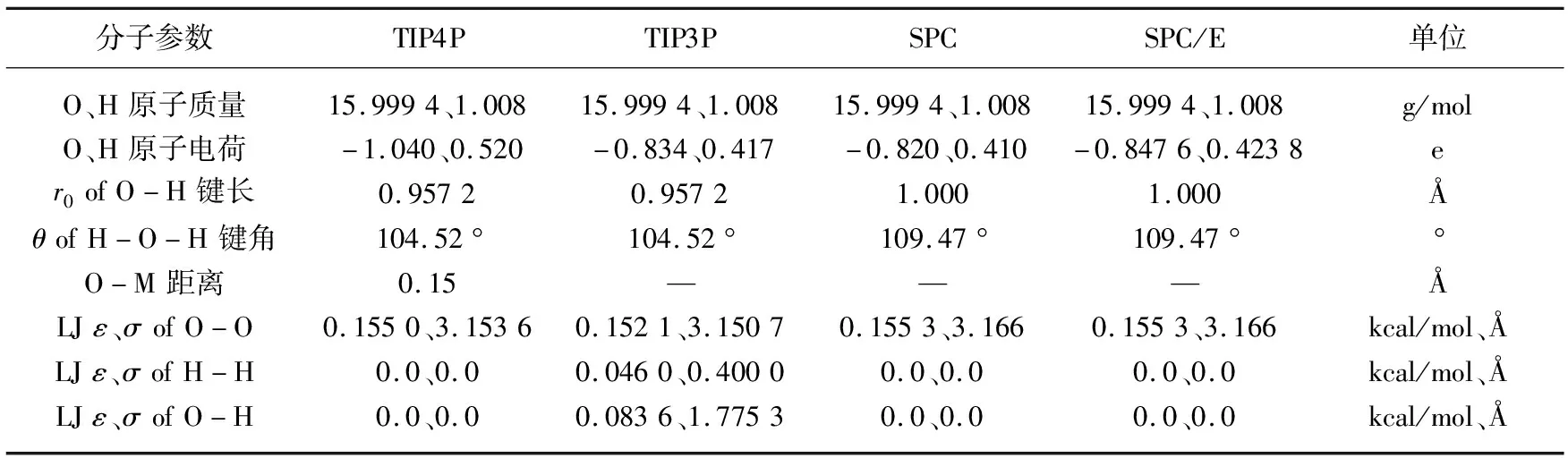
表1 水分子计算参数

2 数值仿真过程分析

2.1 剪切黏度

剪切黏度是黏性动量通量Jz(Px)(以下简写为Pxz)与剪切应变率∂vx/∂z线性关系的系数，是物体黏流性质的具体反映。Green-Kubo线性响应理论给出了输运系数剪切黏度η与黏性动量通量Pxz时间关联的关系[19-24]，如下：

(10)

其中,V是盒子体积，α、β=x、y、z，且β≠α，<>表示取时间平均，Pαβ(t)也被称为系统应力张量P在t时刻Pα在β方向上的分量，其值由Virial定理给出，表达式如下：

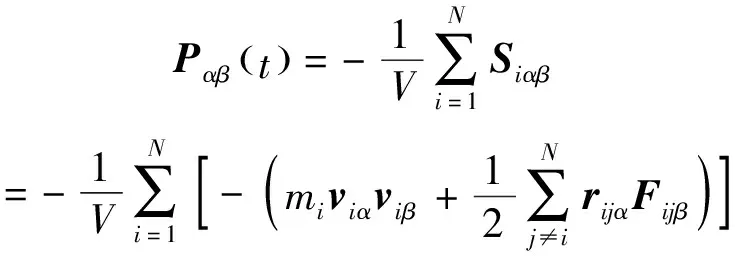
(11)

其中,Siαβ为原子i的原子应力分量，viα为速度在α方向上的分量，rijα、Fijα分别为原子i与j间位移矢量、相互作用力在α方向上的分量。

如图2所示，为了模拟测试SPC、SPC/E、TIP3P以及TIP4P四种水分子模型的剪切黏度η，该仿真系统采用周期性边界条件的正方形盒子，其边长为30a。同样的纳米水相初始位置采用bcc晶格建模，依据水的体相密度ρ=0.997 g/cm3，晶格常数选择为a=3.915 Å。在计算黏度之前，整个体系须执行能量最小化，然后使用Langevin热浴法进行驰豫500 ps。最后去掉Langevin热浴法，在NVE系统下记录500 ps过程中剪切黏度的变化曲线。从图3可以看出，SPC、SPC/E、TIP3P以及TIP4P其相对应的η值分别为0.42、0.57、0.44以及0.62 Pa·s。而在宏观下可以测得η=0.81 Pa·s，由此可见采用TIP4P水分子模型最接近实际值。

图2 不同水分子模型的计算剪切粘度的构型图 图3 不同水分子模型的剪切粘度随时间步变化图

2.2 低速碰撞下的形态演变及静态接触角测量

对初始速度V0=0.003 Å/fs速度下纳米水滴撞击铜表面后，水分子模型采用TIP4P模型，利用数密度图对碰撞过程进行了测量分析。数密度图就是对体系在z方向进行了分层切片(chunk)，切片厚度dZ=2 Å，同时视底层边界中心为中心，将整个体系划分成一个个同心的空心圆柱体，空心圆柱体的宽度bin=2 Å。这样，体系被划分成一个个截面高度为dZ，宽度为bin的长方形环。图4为纳米水滴撞击铜表面润湿的数密度云图演化示意图：图(A)为t*=0.150时刻，液滴刚接触壁面，在其底部中心处有一红色区域，数密度较大，这是撞击造成水分子被压缩，其中t*=0.0为液滴刚接触壁面；在经过图(B)形变后，到达最大湿润长度图(C)βmax≈1.175；随后，液滴在表面张力作用下回缩，经过图(D)和图(E)形变后，在图(F)t*=29.700时刻，液滴完全驰豫平衡在壁面上。

图4 在初始速度V0=0.003 Å/fs速度下纳米水滴撞击铜表面润湿的数密度云图演化

图5(a)左边为数密度等值线图，外轮廓用粗红线标出，右图为其云图。图5(b)给出质量密度分布曲线和静态接触角的测量示意图，如图所示，在其底部存在类固体区，液滴外轮廓形变较大，而在右部存有液气交界区，尽管本文未考虑气体的存在，但也可以看出其质量密度在42.5 Å后急速下降为0 g/cm3。取数密度值为0.06的轮廓L0.06与固溶区的交点并引与L0.06的切线，其与x轴的夹角即为静态接触角θS，得出纳米水滴撞击铜表面后的静态接触角θS为105°。而宏观液滴的静态接触角θS为103°，误差为1.9%，故该方法具有可信度。

图5 数密度分布以及静态接触角

3 结 语

采用分子动力学模拟计算了水的黏度和纳米水滴在固体铜表面上的静态接触角。根据Green-Kubo线性响应理论计算水的黏度的理论公式，比较四种水分子模型SPC、SPC/E、TIP3P以及TIP4P的仿真计算结果。此外，展示了纳米水滴低速撞击的铜表面数密度云图，并通过液滴的数密度等值线图精确计算了液滴平衡时的静态接触角。两个重要的结论如下：

(1)SPC、SPC/E、TIP3P以及TIP4P其相对应的剪切黏度值分别为0.42、0.57、0.44以及0.62 Pa·s。TIP4P水分子模型的计算结果最接近实际值η=0.81 Pa·s。

(2)液滴低速碰撞固体表面会出现铺展和回缩以及弛豫平衡过程。对液滴平衡时的静态接触角的测量值为103°，与实际误差仅为1.9%。