船体梁振动的反共振频率配置设计
2021-02-07史英沙
史英沙,黎 胜,2
(1.大连理工大学 工业装备结构分析国家重点实验室 船舶工程学院,大连 116024;2.高新船舶与深海开发装备协同创新中心,上海 200240)
反共振是指系统的某个自由度在特定的频率激励下的稳态振动幅值为零[1]。在结构振动的频域响应谱中,峰值为结构的共振频率,而最小值为零时,在频域响应谱中表现为谷值,此时的频率即为反共振频率[2]。结构共振是系统的总体现象,反共振为系统的局部现象,反共振频率不仅取决于系统的质量阵和刚度阵,还取决于激励点和响应点的位置。在工程应用中,结构处于反共振频率时,结构某些部位振动消失,因而对反共振频率的研究有着重要的应用价值[3],但因为共振频率和模态振型本质上决定了线性无阻尼系统的基本动态响应特征。因而,目前对结构振动控制的相关研究多集中于对共振频率计算和控制,而对结构反共振频率的关注相对较少,并且目前反共振概念多应用于对系统的隔振控制设计[4-9]。近年来,对船体总振动的研究较少,马广宗等[10]对一万五千吨干货船设计阶段所进行的减振设计工作进行了详细介绍,李维嘉等[11]从隔振,动力吸振,阻尼减振等被动控制和主动控制方面,阐述了船舶振动控制技术的发展。此外部分学者还考虑了不同方法对船体振动的预测分析[12-17]。
本文针对船体梁模型,提出了一种基于反共振频率配置的船体振动设计方法,该方法基于船舶主机等主要激振力,计算得到了船体振动的反共振频率,并将激励频率设置为反共振频率,使得船体梁的上层建筑或桅杆等重要部位的响应为零,并且在配置的反共振频率下,船体垂向振动响应明显减小。本文以一维薄壁混合开闭口船体梁为例,计算了在主机外力矩作用下,上层建筑振动响应为零时的反共振频率,并通过结构修改将主机一阶激励频率配置为反共振频率,并分析了上层建筑的振动响应变化情况,以及在配置的反共振频率下,船体梁的响应变化情况。
1 基本原理
对于无阻尼多自由度系统的运动方程如下:
(1)
式中:M,K分别为系统的质量阵和刚度阵,x为位移向量,f为外激振力向量,且x=Xeiωt,f=Feiωt,所以运动方程可表示为:
(K-ω2M)X=F
(2)
系统导纳H可表示为:
H=(K-ω2M)-1
(3)
所以系统频率响应公式可表达为:
HF=X
(4)
1.1 反共振频率的求解计算
He等[18]用导纳方法求解结构反共振频率的表达式如下:
(5)
式中:Hpq,Kpq,Mpq分别为导纳阵H,刚度阵K和质量阵M中划去第p行和第q列所得到的的导纳子矩阵,刚度子矩阵和质量子矩阵,det为矩阵行列式运算。
由式(5)可知,若要求解系统响应为零时的反共振频率,只需求解:
det(Kpq-ω2Mpq)=0
(6)
同时,使得下式成立的频率为系统固有频率。
det(K-ω2M)=0
(7)
王波平等[2]基于矩阵方法也求得了结构的反共振频率。通常结构响应可表示为物理坐标的线性组合,即响应为Resp=CX,且X=Gq,G为转换矩阵,q为系统的模态坐标,所以当响应为零,即Resp=CGq=0时,可得到G=null(C)。此时系统的运动方程为:(K-ω2M)Gq=F,转换矩阵T=null(FT),系统运动方程左乘TT可得:
TT(K-ω2M)Gq=TTF=(FTT)T=0
(8)
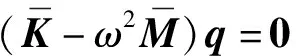
(9)

1.2 质量或刚度修改的反共振频率配置
当系统t处的修改量为bt时,系统的运动方程可表示[3]:
(10)

(11)
式(11)中第t列为
(12)


(13)
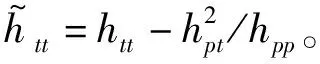
(14)
仅修改质量阵时:
(15)
由以上推导可知质量修改量和刚度修改的关系为:
(16)
1.3 质量和刚度同时修改的反共振频率配置

(17)
其中
(18)
当仅改变刚度时:
(19)
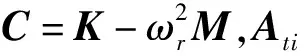
ct1At1+ct2At2+…+cttAtt+…ctnAtn=Δkt(N-M)
(20)
当对t位置刚度修改Δkt后,此时修改表达式为:
(21)
式(21)可表达为:
ct1At1+ct2At2+…+(ctt+Δkt)Att+…ctnAtn=0
(22)
由式(16)可知,质量修改与刚度修改相关。假设在配置反共振频率ωr时,单独修改刚度时修改量为Δkt。若先对刚度K中t位置的修改量为aΔkt,0 (23) 式(23)可表达为: ct1At1+ct2At2+…+ (24) aΔkt+(1-a)Δmt, 0 (25) 因此在同一位置t处同时进行刚度和质量修改时,刚度修改和质量修改占仅改变质量和刚度的比例之和为1。 本文建立了薄壁变截面混合开闭口一维船体梁模型,如图1所示。在该模型中,原点位于船艉,X轴指向船艏,Y轴指向左舷,Z轴垂直向上。该船模共19个单元,20个节点,图(a)为一维船体梁模型,上方标注为梁单元位置,下方标注为节点位置。其中,1节点位于船艉,20节点位于船艏。各梁单元的长度见表1,各梁单元的形状见图(b)和图(c)。其中E=2.01×1011N/m2,ν=0.3,ρ=7.8×103kg/m3,板厚t=0.002 m,船宽b=0.65 m,艏艉船宽bd=0.25 m,型深h=0.32 m。该船模的前两阶垂向振动固有频率(单位:Hz)为77.087,200.770,与文献[19]77.737和207.638相对误差分别为0.84%,3.09%。 (a)一维船体梁模型 在船舶各类总振动中,垂向弯曲振动最易激起,也最为重要,因此在本文中仅考虑船体梁的垂向弯曲振动。该模型共20个节点,每个节点3个自由度,X,Z,绕Y轴转动ROTY,M,K均为60×60的对称正定矩阵。假设主机位于船体梁模型的节点2处,上层建筑位于梁单元(5),两端分别为节点5和节点6。 通常船用多缸柴油机各缸产生的惯性力的合力为零,即柴油机的不平衡力为零,但由于各缸中惯性力作用在曲轴柄位置不同,因而产生的外力矩不一定为零[20]。在本算例中假设主机的外力矩作用于船体2节点(第6自由度),上层建筑6节点处垂向响应最小(第17自由度)。系统的固有频率及在该激励位置和响应位置时,使用导纳H17,6和矩阵方法分别求解得到的反共振频率如表2所示,并可知导纳方法和矩阵方法具有相同精度。 表2 船体梁固有频率及反共振频率 假设该船模主机基频和螺旋桨轴频均为80 Hz,主机的二阶激励频率为160 Hz,四阶激励频率为320 Hz。螺旋桨为3叶,叶频为240 Hz,倍叶频为480 Hz。根据激励频率和频率储备可计算得到船体梁垂向振动的前三阶频率范围,见表3。其中频率储备公式如下: 表3 船体梁固有频率范围 (26) 式中:fe为激励频率,fi为船体总振动固有频率,η为频率储备。按规范[21],其前三阶的固有频率一般应与激励频率分别错开10%~15%,15%~20%,20%~30%。在本文中分别选取为10%,15%,20%。 在选用该主机和螺旋桨的情况下,由表3可知,此时船体一阶垂向固有频率不满足频率储备,需要对船体梁进行修改。把主机一阶激励频率80 Hz配置为船体梁反共振频率,主机外力矩作用于船体梁2节点处,上层建筑6节点的垂向响应为零,通过对船体梁中单元(10)和(11)的Z方向的质量进行调整,使得质量阵中M(32,32)的改变量为Δm32,32=55.576 kg。可对船体货舱进行调整,将此处设置为货舱或压载舱。 图2为在第32自由度处结构修改后,系统导纳H17,6的响应曲线,前三阶反共振频率分别为80.00 Hz,313.56 Hz,497.19 Hz,并且船体梁在80 Hz垂向振动响应如图3,由图可知在6节点处垂向振动响应为零,并且船体梁在80 Hz时的垂向振动响应与修改前相比明显减小,并均接近于零。因此由图2,3可知,质量修改后成功配置出80 Hz的反共振频率。在对船体梁(10)和(11)垂向质量调整使得M(32,32)修改后,其前三阶固有频率分别为64.67 Hz,185.27 Hz,319.94 Hz,由表3可知均满足频率储备,符合设计要求。此外,结构修改后将船体梁的前三阶振型归一化处理,如图4所示。在单元(10)和(11)增加垂向质量的修改后,船体梁的振型变化较为平缓。 图2 第32自由度处结构修改后导纳H17,6响应曲线 图3 80 Hz时船体垂向振动响应 图4 船体梁振型 修改前—— M(32,32)修改后---- 在船体梁(1)和(2)单元中Z方向刚度进行调整使得K(2,2)修改后,反共振频率分别为23.96 Hz,80.00 Hz,126.24 Hz。在80 Hz时,主机外力矩作用于2节点时,船体梁的垂向振动响应如图6所示,在节点6处响应为零,因此由图5和图6可知,在刚度修改后成功配置出80 Hz反共振频率,并且在配置的反共振频率下船体梁的垂向振动明显减小,并接近于零。 图5 第2自由度结构修改导纳H17,6响应曲线 图6 80 Hz时船体垂向振动响应 在船体梁刚度K(2,2)修改后,将船体梁的前三阶振型归一化处理后如图7所示,根据振型可知,在配置的反共振频率80 Hz两侧存在两个一阶振型,分别为43.19 Hz和102.74 Hz,因而船体梁前三阶固有频率分别为43.19 Hz,102.74 Hz,211.52 Hz,361.22 Hz,由表3可知满足频率储备,因而符合设计要求。结构修改后归一化的船体梁振型,图7所示。 图7 船体梁振型 修改前—— K(2,2)修改后---- (a)结构修改后导纳H17,6响应曲线 本文针对船体梁的主要激励,求解得到了船体梁的反共振频率,并提出了一种基于船体反共振频率配置的船体振动设计方法。该方法将主机某阶激励频率设置为反共振频率,对船体结构进行刚度,质量修改,可使得船体的上层建筑或桅杆等重要部位在该反共振频率下振动响应为零,并可明显减小该频率下船体振动响应。通过修改位置的调整,可以改变船体的固有频率,使其满足设计要求,因而该方法对船体总振动设计有一定的参考意义。 此外本文基于船体垂向振动的研究结果发现,在对结构进行修改时,单独修改刚度,质量,以及同时对质量和刚度进行修改都可实现预期反共振配置的效果,同时对质量和刚度进行修改时,在配置的反共振频率下,结构的振动响应与单独修改质量或刚度的效果相同,且在实际工程中刚度和质量修改量与原有仅修改刚度和质量的修改量的比例之和为1。2 数值算例
2.1 船体梁模型



2.2 质量修改

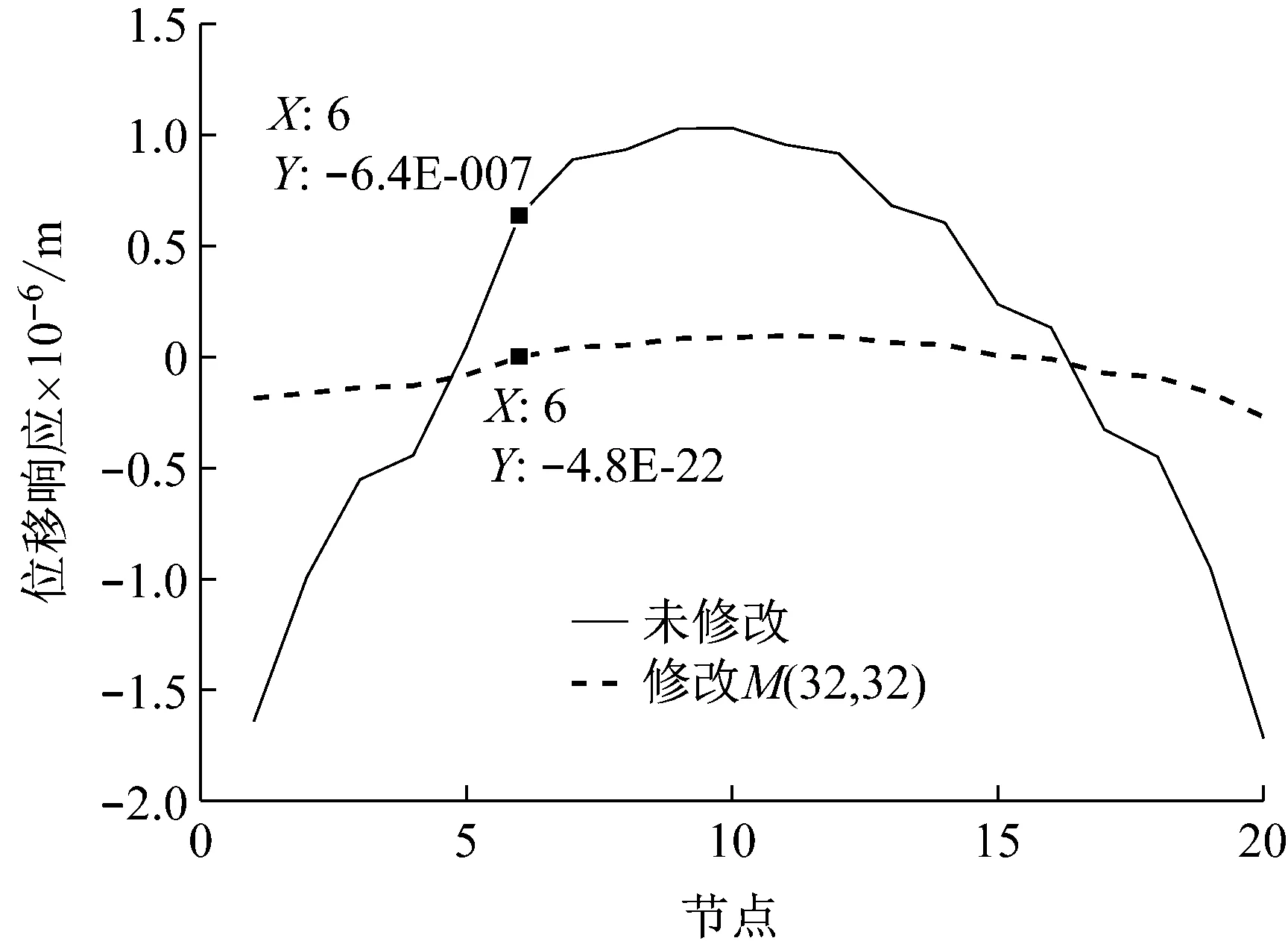

2.3 刚度修改
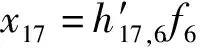



2.4 刚度与质量同时修改


3 结 论
