应用MR阻尼器的连续梁桥地震损伤控制方法

2021-02-07石运东

振动与冲击 2021年3期

陈宇，石运东，吕杨，黄信

(1.中国民航大学机场学院，天津 300300；2.天津大学建筑工程学院，天津 300350；3.天津城建大学土木工程学院，天津 300384)

历次灾害中，连续梁桥在强震作用下发生破坏的现象屡见不鲜，如1989年的Loma Prieta地震[1]、1995年的Kobe地震[2]、1999年的Chi-Chi地震[3]、1994年的Northridge地震[4]均导致了桥梁不同程度的破坏，而桥梁结构作为生命线工程，强震作用下一旦发生倒塌将造成极大的经济损失和社会影响，因此对连续梁桥进行有效地减震控制提高其抗倒塌性能具有重要意义。

试验证明MR阻尼器可有效减小结构的地震响应提高其抗震性能[5]，并且其依靠能耗低、阻尼力大、响应快、连续可调的特点被广泛应用于结构振动控制中[6]。经过多年的研究，国内外学者在MR阻尼器出力模型方面提出了Bingham模型[7]，Bouc-Wen模型[8]，修正的Bouc-Wen模型[9]，Nonlinear hysteretic模型[6]等；在控制策略方面提出了Bang-Bang控制[10]，Clipped-Optimal半主动控制策略[11]、模糊控制[12]等；在结构减震控制方面，Yang等[13]采用试验方法验证了MR阻尼器对悬索桥主梁纵桥向的位移具有很好的控制效果；Sahasrabudhe等[14]应用数值和试验的方法对隔震桥梁采用MR阻尼器进行振动控制，结果表明MR阻尼器可以有效减小桥梁的支座位移；Lin等[15]提出基于信赖域的控制算法采用MR阻尼器对大跨度结构进行了地震控制并取得了较好的控制效果；在阻尼器优化出力及布置方式方面，吕杨等[16]优化设计了MR阻尼器出力方案，实现了建筑结构地震损伤最优控制；阎石等[17]提出了阻尼器在结构中优化布置的一些基本原则，一定程度上起到了优化阻尼器控制效果的作用；张延年等[18]提出了磁流变阻尼器和滑移隔震混合方案，采用IHGA程序对混合方案进行了优化设计，更好地控制了结构的地震反应。强震作用下结构往往进入塑性损伤阶段，而结构的损伤破坏分析需考虑材料、几何等强非线性，传统的桥梁结构控制方法一般仅关注结构动力响应的控制效果，对强震作用下结构进入非线性阶段的控制效果的研究较少。强震作用下一个桥墩发生破坏将极大影响桥梁整体结构的安全性，如果地震作用下每个桥墩发生不发损伤或发生的损伤趋于平均化且在可控范围内，这将有助于提高桥梁整体的抗震性能，因此寻找有效的优化控制方案充分利用阻尼器减小结构的地震响应并避免桥墩损伤集中尤为重要。

本文通过LS-DYNA有限元程序二次开发了课题组研制的MRF-04阻尼器，将桥梁精细化模型和阻尼器进行一体化建模建立了一三跨钢筋混凝土连续梁桥的数值分析模型，结合桥墩损伤模型设计了各桥墩基于广义水平刚度比的MR阻尼器出力方案，并精细化模拟分析了采用MR阻尼器对地震作用下连续桥梁的控制效果以及所提出方法中的设计传递系数对控制效果的影响。

1 阻尼器优化设计

1.1 桥墩损伤模型

基于MR阻尼器的桥梁结构地震损伤控制方法是以桥墩构件的损伤模型为基础而设计的阻尼器出力优化方案，其方法的建立首先需确定桥墩构件的损伤模型。李忠献等[19]提出基于材料损伤的钢筋混凝土墩柱构件损伤模型可以很好地模拟和评价桥墩构件的力学性能，其桥墩构件的损伤模型为：

(1)

由于桥梁结构为串联体系，因此定义桥梁结构的整体损伤准则为：

(2)

式中,m为桥墩个数。

文献[19]定义了钢筋混凝土柱的损伤等级为5级，各等级所对应的损伤指数,如表1所示。

表1 损伤等级对应的损伤指数

1.2 MR阻尼器出力设计

桥梁结构体系中，各桥墩对桥梁结构整体抗震性能贡献不同，具体表现为各桥墩对桥梁整体提供的水平刚度不同。为了使桥墩在地震作用下协同工作并考虑桥墩的损伤破坏导致其刚度退化，各桥墩安装的阻尼器出力按下式确定：

(3)

式中：Fi为第i桥墩安装的阻尼器设计最大出力，Fa为所有桥墩设计的最大出力之和，di为第i个桥墩的损伤值，ki为第i桥墩的广义水平刚度。

本文对地震作用下桥墩简化侧向力分布模式进行弹塑性分析，求解其广义水平刚度ki。其具体计算步骤如下：

(1)计算桥墩构件的动力特性参数。将桥墩构件离散为n个质点的集中质量模型如图1所示，求解桥墩的圆频率和振型；

(4)

(5)

式中：κi为主梁惯性力作用于第i桥墩的分配系数，M为主梁质量，γ为主梁惯性力系数，其公式为γ=α/β，α为相应抗震水平的水平地震最大影响系数，β为主梁设计传递系数。

(3)计算各桥墩广义水平刚度。基于各桥墩广义水平刚度比等于其所受墩顶水平集中力比的假定，按公式(6)非线性迭代求解各桥墩的分配系数κi，进而求解各桥墩在确定的侧向力分布模式下广义水平刚度。

(6)

式中：ki(·)为按第(2)步侧向力分布模式计算的第i个离散为n个质点桥墩的广义水平刚度。

1.3 MR阻尼器力学模型

李忠献等根据阻尼器的工作模式设计出一种剪切阀式磁流变阻尼器，命名为MRF-04K阻尼器，其具有很好的鲁棒性，并在Spencer提出的模型的基础上建立了适合MRF-04K的修正Bouc-Wen模型，该模型的控制方程为：

(7)

(8)

由方程式(7)和(8)可得：

(9)

式中修正的Bouc-Wen单元为：

(10)

式中：x(t)为阻尼器活塞的位移，y(t)为阻尼器的内位移变量，F(t)为阻尼器出力，α，c0，c1为所加电压u的二次函数，通过下式计算得到：

(11)

1.4 半主动控制算法

MR阻尼器开关控制算法可以有效耗散地震能量[20]，减小地震的残余位移，并且为了实现MR阻尼器对钢筋混凝土桥梁的地震损伤进行控制，本文将MRF-04K阻尼器二次开发进入LS-DYNA有限元程序中，采用开关控制算法其表达式为：

(12)

2 桥梁分析模型

某一联三跨钢筋混凝土连续梁桥，跨径布置为90 m+160 m+90 m，主梁为钢筋混凝土空心箱梁，边墩处主梁的截面高度为3.85 m如图3:1-1，中墩处主梁截面高度为9.375 m如图3:2-2，边墩和中墩为单箱单室空心薄壁桥墩如图3:3-3和4-4，2号桥墩为固定墩其固定支座最大水平抗力为4 500 kN，1～4号墩均设置抗震刚性挡块，该桥梁所处抗震设防烈度为9度，水平地震最大影响系数为1.4。

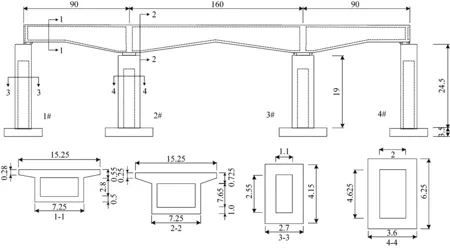
图3 桥梁模型

混凝土采用C40，桥墩纵向钢筋直径分别为25 mm，纵筋间距为150 mm，箍筋直径为16 mm，箍筋间距为150 mm，桥墩混凝土保护层厚度为60 mm。桥墩和箱梁采用纤维单元，钢筋采用等效纤维单元建模方法[21]，混凝土采用单轴Faria-Oliver损伤本构模型，钢材采用弹塑性本构模型。

3 控制效果对比分析

3.1 无控方案与半主动控制方案对比

无控方案(UNC)为桥梁结构中桥墩与主梁设置抗震刚性挡块；半主动控制方案(SEM)为沿纵桥向各个桥墩在墩梁间设置阻尼器(如图4)，并且未设置刚性抗震挡块。主梁的总重量为190 MN，设计主梁最大传递系数β=0.12，中墩和边墩按所提出的方法设计阻尼器出力按公式(1)～(6)计算，计算得到中墩(2#和3#)设计阻尼器最大出力为9 408 kN，边墩(1#和4#)设计阻尼器最大出力为1 988 kN，在实际工程中由于受到阻尼器规格限制难以实现设计最大出力值，可通过设置多个小规格阻尼器并联组成实现设计目标。

图4 阻尼器布置方式

分别采用Loma Prieta地震动、Taft地震动和Chi-Chi地震动，对无控结构和受控结构进行强震动力IDA分析(加速度峰值调整为0.6 g、0.7 g、0.8 g、0.9 g)，其边墩和中墩的损伤指数如图5所示。从图5可以看出，不同地震动作用下无控结构随着输入地震动强度的增加，中墩损伤指数均出现明显的增大现象；在加速度峰值为0.7 g以上的各地震动作用下无控结构边墩均处于基本完好状态，中墩均处于轻微破坏，而各强度地震动作用下受控结构的边墩和中墩均处于基本完好状态，各桥墩损伤分布趋于均匀。从图5可以看出，三条地震动作用下受控结构的中墩和边墩的损伤指数大大降低，尤其中墩0.7 g以上地震作用下桥墩损伤从轻微破坏过渡到基本完好状态，其原因是由于各桥墩阻尼器出力按公式(3)设计，中墩刚度大、延性较差导致设计的中墩阻尼器出力折减较大，中墩提供给桥梁结构整体的抗侧刚度降低，主梁传递给桥墩的地震力减小，因此中墩损伤指数减小。另一方面，受控结构墩梁间阻尼器在地震作用下发生往复运动消耗大量地震能量，降低了中墩和边墩的损伤程度，使得结构在强震作用下仍然能够保持基本完好的状态。

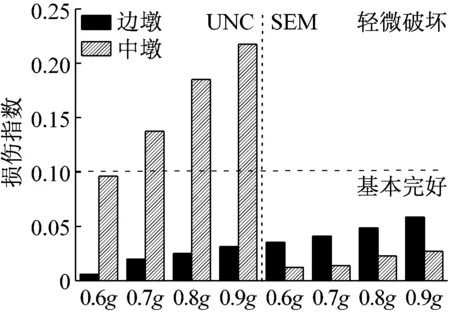
(a)Loma Prieta地震动

3.2 不同控制方案对比分析

根据连续梁桥的震害结果，墩梁相对位移、墩梁残余位移和桥墩损伤指数是桥梁结构控制的主要参数。控制墩梁相对位移有利于保护支座，控制墩梁残余位移有利于快速恢复通车，控制桥墩损伤指数有利于保证结构的安全。分别采用PON控制和半主动控制(SEM)方案对受控结构进行强震动力IDA(0.6 g、0.7 g、0.8 g、0.9 g)分析，进一步研究强震作用下半主动控制的可靠性。其中，PON控制为MR阻尼器输入最大常电流保持最大出力的一种被动控制方案。

图6～8分别给出了不同强度的三条地震动作用下桥梁结构的地震响应及损伤指数。从图中可以看出三条地震动随着强度的增加，墩梁相对位移，墩梁残余位移和桥墩损伤指数均增大。SEM控制方法可以控制墩梁残余位移在三条地震动作用下均处于50 mm以下，而PON控制方法在不同强度的Loma Prieta地震动作用下均大于0.4 m，因此SEM控制方法可显著降低墩梁相对位移，将大大有利于强震过后桥梁快速恢复通车的安全性；同时可以看出，SEM控制下的墩梁相对位移较PON控制增大0.6%～4.4%，其SEM控制效果略差于PON控制；SEM控制下的桥梁损伤指数较PON控制减小9%～97%之间，其SEM控制效果明显优于PON控制。发生上述现象的原因是由于PON控制控制方法阻尼器恒定输出，较SEM控制方法桥墩在地震过程中提供桥梁结构的抗侧刚度大，可降低墩梁之间相对位移，但会增大桥墩墩顶水平力导致桥墩发生损伤破坏；SEM控制方法利用结构振动的往复相对变形和速度调节作动器的控制力，相比PON控制方案，作动器的耗能能力增加，可以达到同时减小墩梁相对位移和降低桥墩损伤的目的。在桥梁设计中桥墩发生破坏难以修复，设置允许位移较大的支座并增加主梁搭接长度可以满足弥补SEM相对位移较大的缺点，并且即使支座发生破坏相对桥墩破坏也易于修复，支座先于桥墩破坏也是桥梁设计的基本原则。因此综上述分析SEM控制优于PON控制。

图6 不同强度Loma Prieta地震动作用下桥梁地震响应及损伤指数

图7 不同强度Taft地震动作用下桥梁地震响应及损伤指数

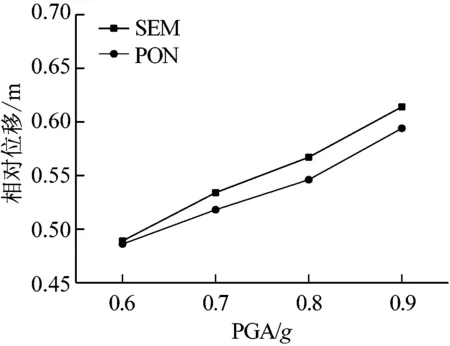
图8 不同强度Chi-Chi地震动作用下桥梁地震响应及损伤指数

3.3 不同设计传递系数的半主动控制效果对比

分析不同设计传递系数β对受控结构控制效果的影响，分别选用β为0.06、0.12、0.18、0.24，中墩和边墩阻尼器出力设计值,如表3所示。

表3 阻尼器出力设计

采用半主动控制方案对受控结构进行强震动力损伤分析，输入地震动的峰值加速度为设计的罕遇地震强度(0.6 g)，边墩墩梁相对位移及桥梁损伤指数如表4所示。从表4可以看出，随着设计传递系数增大，边墩墩梁相对位移减小，说明阻尼器总出力越大对墩梁相对位移控制效果越好；设计传递系数为0.12～0.24，桥梁损伤指数逐渐增大，说明设计传递系数越大桥梁损伤的控制效果越差，尤其β为0.18增加到0.24时，桥梁损伤指数急剧增大，增加幅度至少达184%，其原因是β过大，传递给桥墩的主梁惯性力过大引起桥梁损伤指数明显增加；当β为0.06时，Loma Prieta地震动作用下支座位移达到1 m以上，其原因是β过小，阻尼器耗能相对较少，导致主梁位移过大；当β从0.06增加到0.12时，三条地震动作用下桥墩损伤指数均减小，其原因是随着β增加，主梁对桥墩约束增强，可以有效减小边墩(柔性墩)的损伤指数；而后随着β增加，桥墩损伤指数增加，主梁位移减小，当β为0.18时，三条地震动作用下桥墩损伤指数均小于0.1属于基本完好状态，属于设计可接受范围，因此该控制方案中β取0.18相对较好。