基于频响函数奇异值的模型修正方法

2021-02-07曹明明彭珍瑞刘满东

振动与冲击 2021年3期

曹明明，彭珍瑞，刘满东

(兰州交通大学机电工程学院，兰州 730070)

有限元模型修正技术的发展，使有限元模型与实际结构的参数误差缩小，提升有限元模型模拟实际结构的能力，这对结构健康监测、结构优化设计、预测等工程应用具有重要意义。而且有限元模型精度的提高可以减少不必要的试验，这可以节约成本及缩短研发周期[1]。近年来，基于模态参数和基于频响函数(FRF)的修正方法在结构动力学模型修正中较为常见[2]，基于模态参数的模型修正方法需要模态参数识别，所以在这个过程中不可避免地会引入识别误差。而且，在某些情况下，在工程试验中模态参数的识别误差比有限元模型建模误差还大[3]。而基于频响函数的模型修正方法避开了结构模态分析，直接利用试验测量得到的频响函数来进行模型修正，从而避免了人为引入误差导致最后修正效果较差，而且这种方法适合于修正模态分布相对密集的结构[4-5]。

不管用何种方法，目前结构有限元模型修正技术通常是经过大量的迭代优化搜索来实现的，在这个过程中需要反复的调用有限元模型进行解析计算，但是对于一些大型复杂结构，解析计算其有限元模型不仅需要花费大量时间，而且对于计算机的性能要求比较高，甚至有些求解无法实现。于是，作为一种可以替代有限元模型进行快速分析的代理模型技术，引起了众多学者的关注。代理模型通过建立一个显式的函数来代替模型参数与结构响应之间复杂的隐式关系，也称为近似模型、响应面模型或元模型，近年来逐渐被应用到结构模型修正与确认中[6]。常用的代理模型有响应面法(Response Surface Methodology,RSM)、径向基函数(Radial Basis Function,RBF)、神经网络(Neural Network,NN)、支持向量回归机(Support Vector Regression,SVR)、Kriging模型等[7]。Kriging模型是基于Kriging插值技术的一种等效模型，与其他代理模型不同的是，Kriging模型除了能给出对未知函数的预估值，还能得到预估值的误差估计[8]，只用少量的样本就可以较准确的描述结构输入与输出间的关系，在航天飞行器设计和结构优化设计等领域应用较为广泛。文献[9-10]将Kriging方法应用于频响函数模型修正中，减少了求解时间，提高了频响函数模型修正的效率。

频响函数包含了大量频率点的数据信息，所以频率点的选择对基于频响函数的模型修正方法至关重要，但是目前对于频率点数据的选择方法仍是无法统一。张勇等[11]将频响函数变换为时域内的脉冲响应函数，通过对脉冲响应函数的重构相空间矩阵进行截断奇异值分解(Singular Value Decomposition，SVD)，提取前若干较大奇异值作为原频响函数的特征量来进行模型修正。这种方法间接使用频响函数来进行模型修正，既保留了使用频响函数进行模型修正的优点，又避免了频率点的选择难题。文献[12]中比较了对信号通过连续截断和重构吸引子构造矩阵进行奇异值分解优劣性，发现第二种构造方法，矩阵具有良好的消噪效果，能够有效地消除信号中的随机噪声，并且还具有弱信号提取能力。文献[13]提到使用脉冲响应函数在判断奇异值分解时的有效秩的阈值时具有优越性。但是使用脉冲响应函数首先要将频响函数进行正、逆傅里叶变换，这无疑加大了计算量。而且在不同噪声水平下受噪声影响的奇异值个数是变化的，恰当的奇异值个数不仅能保留住信号的主要特征信息，还能削弱随机噪声的干扰，所以需对保留的奇异值个数进行选择。文献[14]通过直接利用频响函数构造吸引子矩阵进行奇异值分解，并利用重构信号中极值点数量突变点来选取有效秩，成功的对信号进行了降噪。

在上述背景下，为避免正、逆傅里叶变换，提高计算效率，同时避开频率点的选择难题，本文直接利用计算得到的频响函数重构吸引子矩阵，对其进行奇异值分解。根据极值点数量突变原则选择保留主要特征信息的奇异值个数，以模型设计参数作为输入，保留的奇异值作为结构响应，并通过粒子群优化算法对Kriging模型相关系数进行寻优来构建Kriging代理模型。以实测的频响函数奇异值与代理模型输出奇异值差值的平方最小作为目标函数，通过布谷鸟算法求解模型待修正参数。数值算例表明了本文方法的有效性，特别是对于随机噪声的鲁棒性。

1 频响函数特征量选取

1.1 频响函数理论

频域内，一个n自由度阻尼系统在简谐激励作用下的运动方程可以表示为：

(-ω2M+iωC+K)X(ω)=F(ω)

(1)

式中:M、K和C分别表示质量矩阵、刚度矩阵和阻尼矩阵；ω为激励频率；F(ω)为简谐激励；稳态响应X(ω)可表示为：

X(ω)=H(ω)F(ω)

(2)

式中，H(ω)为频响函数。其中，频响函数矩阵为：

H(ω)=(-ω2M+iωC+K)-1

(3)

1.2 奇异值分解理论

将一离散原始信号X=[x1,x2,…,xN]，利用相空间重构理论重构吸引子(Hankel)矩阵：

(4)

式中：n=N-(m-1)τ；A为m×n阶的Hankel矩阵；τ为延迟步长，一般取τ=1；m为嵌入维数，当N是偶数时，m=N/2，当N是奇数时，m取中值[15]。

对Hankel矩阵A进行奇异值分解可得到：

A=UΣVT

(5)

式中:U与VT为正交矩阵；Σ=diag(σ1,σ2,…,σk)为对角阵；σi(i=1～k)为矩阵A的奇异值，σ1≥σ2≥…≥σk≥0，k=min[(m-1)τ+1,n]。

给定阈值λ，可以将式(5)写成如下形式：

(6)

(7)

奇异值分解技术多用于消除测试信号中随机噪声的干扰，后k-r个奇异值通常较小，往往是噪声信号。由于实测频响函数中不可避免的会出现随机噪声干扰，所以对于实测频响函数而言，选择前r个奇异值作为频响函数特征量可以有效消除噪声的干扰。

1.3 极值点数量突变原则

由上可知，选择奇异值的个数r是很重要的，恰当的奇异值个数不仅能保留住信号的主要特征信息，还能削弱随机噪声的干扰。本文利用文献[14]所提极值点数量突变原则选择有效奇异值个数。其基本原理为：理想信号通常是一条光滑的曲线，而当信号受到噪声干扰时，会有大量“毛刺”的出现。所以要使噪声干扰最小，可以通过对重构信号中“毛刺”的数量最少来确定，即信号中的极值点数量最少，而信号中“毛刺”数量随保留奇异值数目的变化而变化，选取极值点数量突变点处奇异值数目作为有效奇异值数目。

综上，本文考虑直接利用计算得到的频响函数重构吸引子矩阵，对其进行奇异值分解。根据极值点数量突变原则选择保留主要特征信息的奇异值，用其表征原频响函数来进行模型修正。

2 基于Kriging模型的模型修正理论

2.1 Kriging模型的建立

Kriging模型是一个基于随机过程的代理模型，包含线性回归部分和非参数部分：

(8)

式中:β为回归模型系数；f(x)为样本点x的多项式函数；z(x)为服从正态分布N(0,σ2)的随机过程。任意两样本点的z(x)之间的相关性可以表示为其空间距离的函数，选计算效率较好的高斯函数为相关函数，其形式如下：

(9)

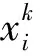
根据极大似然函数法，可以求得：

(10)

(11)

式中:F为样本点的向量组成的矩阵；Y为样本点响应组成的列向量；R为空间相关矩阵，其中元素Rij=R(xi,xj)(i,j=1,2,…,n)，n为试验点数；σ2和β均为θk的函数，那么Kriging模型中唯一未知数即为相关系数θk，其决定着预测响应精度，本文采用粒子群算法对相关系数θk进行寻优。

(12)

式中，rT(x0)=[R(x0,x1),R(x0,x2),…,R(x0,xn)]

浅谈道路桥梁施工的常见问题及质量检测技术的应用…………………………………………………… 田文泽（11-100）

2.2 粒子群算法优化Kriging模型

Kriging模型中的相关系数θk决定着预测响应值精度，只有当所建立Kriging模型精度足够高时，代理模型对修正结果的误差影响才会最小。所以相关系数的确定对于构建代理模型至关重要。游海龙等[16]讨论了利用传统数值优化方法确定Kriging模型相关系数存在依赖搜索起始点等缺点，并利用遗传算法对相关系数进行了寻优，解决了对于起始点的依赖问题。粒子群算法(Partical Swarm Optimization,PSO)[17]由Kennedy和Eberhart提出,属于进化算法的一种,具有算法结构简单、寻找最优解速度快的优点。根据以上分析，本文打算利用PSO优化Kriging模型相关系数构建满足修正要求精度的Kriging模型。首先采用拉丁超立方抽样方法抽取一定数量的样本点，然后把抽取的样本点分成训练集和测试集。以训练集作为Kriging模型的输入变量，以所保留的r个奇异值作为响应值来构建Kriging模型，以测试集Kriging模型的均方误差(Mean Squared Error,MSE)均值平均值作为粒子群算法的适应度函数，寻得最优相关系数。最后以训练集作为样本点建立Kriging模型。

2.3 模型修正流程

当Kriging模型构造完成时，模型修正归根结底是一优化问题，在目标函数最小的条件下，通过求解该优化问题，得到设计参数的修正值。目标函数为：

(13)

在优化求解时，除了灵敏度方法外，智能算法也是很简便的。布谷鸟算法[18]由于特有的莱维性能，使其具有较强的全局搜索能力，而且它参数少，操作简单，易于实现，寻优性能佳。故本文选用布谷鸟算法进行优化求解。模型修正流程如图1所示。

图1 模型修正流程图

3 数值算例

3.1 算例一

通过一个车辆三自由度垂向频率响应模型来验证本文方法，该模型如图2所示。

图2 车辆三自由度垂向频率响应模型

图中k3和c2为二系悬挂刚度和阻尼，k2和c1为一系悬挂刚度和阻尼矩阵，k1为减震器端部刚度(串联刚度)，c1、m1和k1组成了一个完整的减震器模型，m2为转向架质量，m3为车体质量。

系统运动方程为：

(14)

以上文提到的数据为理论模型参数，试验验证参数将减震器端部刚度k1减小20%，将二系悬挂刚度k3增加20%。以这两个参数为修正设计参数，在其理论模型初始值的±40%变化区间里，采用拉丁超立方抽样抽取80个样本点。用前40个数据作为训练集，后40个数据作为测试集。采用前文所述方法进行模型修正，修正结果如表1所示，其第1个奇异值得到的拟合响应曲面，如图3所示。

表1 车辆三自由度系统的模型修正结果

图3 车辆三自由度系统的Kriging响应面

由图3可知Kriging模型中样本响应和预测响应重合度很好，由表1可知用本文方法进行模型修正所得修正误差很小，证明用奇异值来表征频响函数作为结构响应进行模型修正是有效的，并且也达到了很高的修正精度。

3.2 算例二

实际试验中，测试数据不可避免的会受到噪声的干扰。所以为进一步验证本文方法对噪声的抗干扰性，选择一三维桁架结构来验证。该结构包括28个节点，66个单元和48个自由度。桁架约束条件为4个支座固定(节点编号1,8,9,16)，节点铰接，每个节点只考虑竖向Y和横向Z的平动自由度。再运用动力学计算其质量矩阵、刚度矩阵，将其代入式(3)中计算出其频响函数矩阵。由于本文所用方法避开了频率点选择问题，只需保证频响函数在感兴趣频带内有足够数量的共振峰，所选结构的激励点和响应点如图4所示，桁架结构参数,如表2所示。

表2 三维桁架结构参数表

图4 三维桁架模型结构图

用表2中的模型参数作为“试验模型”参数，以所有杆的弹性模量和密度作为修正变量，然后对“试验模型”参数中修正参数偏移得到“有限元模型”。弹性模量增加10%，材料密度减小10%，得到的对应的有限元模型参数值,如表3所示。

表3 试验模型和有限元模型参数

采用拉丁超立方抽样在上述有限元模型两个参数(弹性模量、材料密度)的±20%区间内抽取80个样本进行模型修正。图5为用粒子群算法进行Kriging模型相关模型参数寻优的适应度曲线，由图5可知当进化代数为31次时，适应度曲线达到收敛，寻得最优值。图6为Kriging模型在第1个奇异值处得到的拟合响应面和MSE曲面。

图5 粒子群优化适应度曲线

由图6(a)可以看出Kriging模型中样本点都落在了所构建的响应面上，其与预测响应重合度较高。而且MSE值最大也小于3×10-13，可见所构建的代理模型精度很高。

(a)奇异值响应面

Kriging代理模型构造完成之后，便可以代替有限元模型进行迭代寻优。假定试验参数值在有限元参数值的±25%区间内，使用布谷鸟算法进行迭代寻优。鸟巢数为20，最大迭代次数为100。为了证明算法的稳定性，算法运行30次，取其中的误差最优的一次、最差的一次和将30次取平均，迭代收敛曲线,如图7所示。模型修正结果,如表4所示。

由图7可以看出，布谷鸟算法寻优能力稳定，迭代次数为40之前就可以收敛，30次寻优结果中最优值和最差值差别也很小。由表4可以看出使用本文所提方法在没有噪声干扰的情况下达到了很好的修正效果。使用所得修正参数的修正值，Kriging模型、试验模型及有限元模型频响函数曲线,如图8所示。

图7 迭代曲线

表4 模型修正参数及误差

图8 Kriging模型、试验模型及有限元模型频响函数曲线

由图8可以看出修正过后的结构频响函数与试验频响函数几乎重合，与有限元模型频响函数形状相似，只是沿坐标轴有一定的移动。

为进一步检验本文修正方法的修正效果，比较频响函数修正前后实、虚部曲线，如图9所示。由图9可以看出修正后的有限元模型无论是实部还是虚部，都能很好的与试验模型的频响函数曲线重合。这进一步证明了本文所提方法的有效性。

(a)实部曲线

由于试验测得的频响函数不可避免的会受到噪声的干扰。所以为了验证本文在抗噪性方面的性能，在目标频响函数中加入高斯白噪声，信噪比分别为30 dB、20 dB、10 dB和5 dB，如图10所示。

(a)信噪比30 dB

由前文理论可知，对于受到噪声干扰时频响函数的较小奇异值往往是噪声信号，所以本文选择奇异值来表征频响函数时，应当选择合适的奇异值数目，将噪声信号尽可能的消除，保留有效的奇异值，这样模型修正的误差也会尽可能的减小，所以选择合理的阈值相当重要。根据前文所提极值点数量突变点原则来选择合理的阈值，不同信噪比下极值点数量突变点如图11所示，在各信噪比情况下，程序运行10次的模型修正结果均值,如表5所示。

表5 不同信噪比下修正结果

图11为在不同信噪比下保留不同奇异值进行信号重构以后，信号中所对应的极值点数量。然后根据算出的极值点数量的突变点来确定有效奇异值的个数，由图11可以看出在信噪比分别为30 dB、20 dB、10 dB和5 dB情况下选出的奇异值个数分别为55、37、20、12。图中极值点数量在不同信噪比情况下，前面和后面变化平稳，前面极值点数量较少，后面极值点数量多，这说明前面奇异值是受噪声影响较小的有效奇异值，后面是受噪声影响较大的奇异值。并且随着信噪比的降低有效奇异值个数逐渐减小，这也符合前文所说当信号随着噪声污染加大时，能表征频响函数的有效奇异值数目逐渐减少。

(a)信噪比30 dB极值点数量突变点

由表5可以看出在相同信噪比情况下，选择奇异值数目比不选奇异值数目修正误差小，尤其是当信噪比逐渐减小时，误差尤为明显。而且随着噪声干扰加大，选秩的修正误差变化不大，而不选秩的修正误差变化较大。当信噪比较高时，不选秩所得修正误差不是那么大，这表明用奇异值表征频响函数本身就有一定的抗噪性。当信噪比为5 dB时选秩的修正误差也低于3%，由此也说明了本文方法对于噪声干扰大时的有效性。