硅纳米锥阵列结构参数对抗反射性能研究

严鑫，黎相孟, 2，赵泽鹏，刘晨华

(1. 中北大学 机械工程学院，山西 太原 030051； 2. 西安交通大学 机械工程学院，陕西 西安 710049)

0 引言

蛾眼结构是利用光波长对等于或者小于自身周期结构辨别能力弱的特点，对于光波可以近似成折射率渐变的介质来减少光的菲涅尔反射。1973年第一个人工抗反射微纳结构[7]被制造出来。蛾眼结构是多层薄膜的进阶形式，但不同于传统的多层薄膜增透，蛾眼结构克服了多层薄膜的一系列缺点，并且可以实现宽波段与广角度的增透[8-9]。纳米锥形阵列作为蛾眼结构的一种，通过在单晶硅基板上刻蚀出纳米锥形阵列可以实现宽波段上的抗反射效果[10]，同时纳米锥形阵列结构属于太阳能硅基板的一部分，不存在由于增透结构与基底的热匹配性能较差而引起薄膜的裂纹与脱落[11]。之前有文章介绍了纳米锥形阵列结构的制备方法，并且测量了部分样品的反射率[12]，由于实验是有穷性的，并未对纳米锥形阵列结构的抗反射规律进行分析，对于其增透机理也并未过多解释。本文利用数值仿真的方法对锥形阵列结构的抗反射规律进行分析研究，在此基础上进行结构参数的优化，分别建立3种模型并进行分析研究，得到具有优越抗反射性能的锥形阵列结构。

1 模型建立以及数值方法分析

实验中制备的硅锥形阵列结构如图1(a)所示，图1(b)为使用FDTD Solutions软件建模而成的仿真模型，图1(c)为结构参数示意图，A为阵列周期，Db和Dt分别为底端直径与顶端直径，Z为阵列高度，n1，n2，…，nt,nt+1为各膜层的折射率。

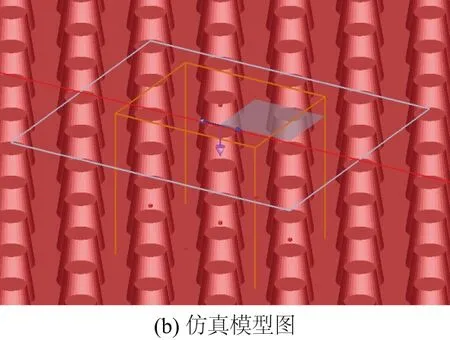
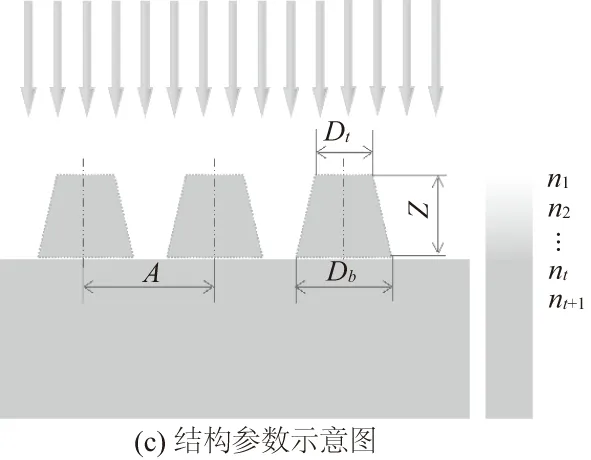
图1 硅锥形阵列结构、仿真及结构参数图

使用正入射平面波光源作为仿真光源，光源的波长设置为0.3μm～1.2μm。在数值仿真中仿真模型边界条件的设置极为重要，图2为纳米锥阵列结构反射电场x方向与y方向的分量图，模型的电场分布在x和y方面分别为对称与反对称分布，所以在x、y方向分别设置为对称与反对称的边界条件。

纳米锥形阵列结构的蛾眼结构是替代多层渐变薄膜的，其折射率的变化是渐变的。在光波正入射时，光的反射率由菲涅尔方程可得

(1)

其中：R为反射率；n1、n2分别为两个相邻两介质的折射率。由式(1)可知两介质材料的折射率相差越小，反射光的能量也就越小。硅纳米锥形阵列的渐变效果由空气的折射率数值渐变到硅基板的折射率数值来反映的，如图1(c)所示。当入射光为正入射时，多层薄膜的反射系数为

(2)

其中：m11、m12分别为多层膜的传输矩阵系数；n0、nt+1为多层膜对应层数的膜层折射率[13-14]。

每一个波长对应的折射率渐变效果是不同的，对应的膜层数以及每层的折射率也不相同，由式(1)、式(2)可以得到，对各个波长进行单独研究，会造成分析过程冗杂。本文基于太阳能发电设备的特性，采用0.3μm～1.2μm整体波段上的平均反射率作为目标函数进行研究分析。

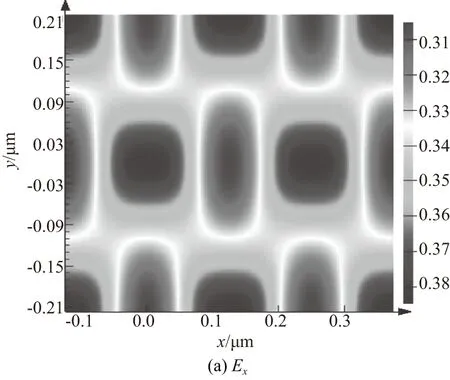
图2 电场的x、y方向分量

2 仿真结果分析

仿真分别选择了实验中250nm、400nm与800nm粒子直径自组装刻蚀形成的形貌参数,建立了模型1、模型2与模型3。各个模型的阵列结构参数如表1所示。研究范围与每个模型自身的参数有关，参照表2。

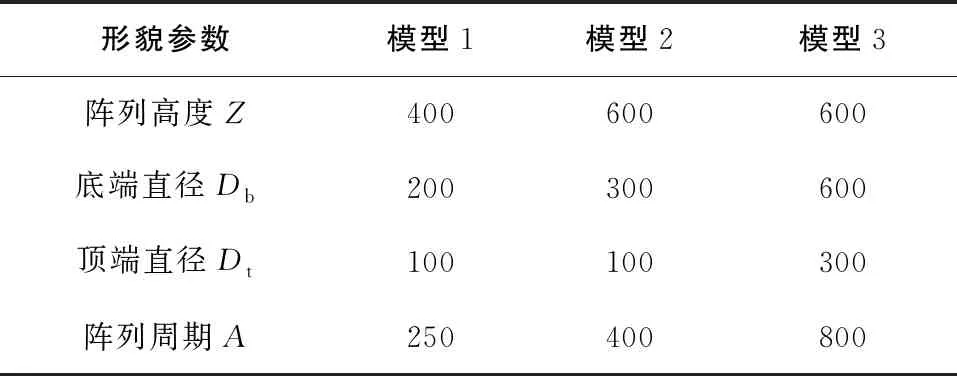
表1 锥形结构的模型参数 单位：nm

表2 纳米锥形阵列结构参数研究范围 单位：nm

图3为3个初始模型与未经加工硅基板的光反射率对比图，相较于未经加工硅基板43.29%的平均反射率，模型1、模型2与模型3的平均反射率分别为15.20%、17.40%、12.84%。平均反射率均明显降低，实现了0.3μm～1.2μm全波段的增透，表明3个模型具有较强的抗反射性能。

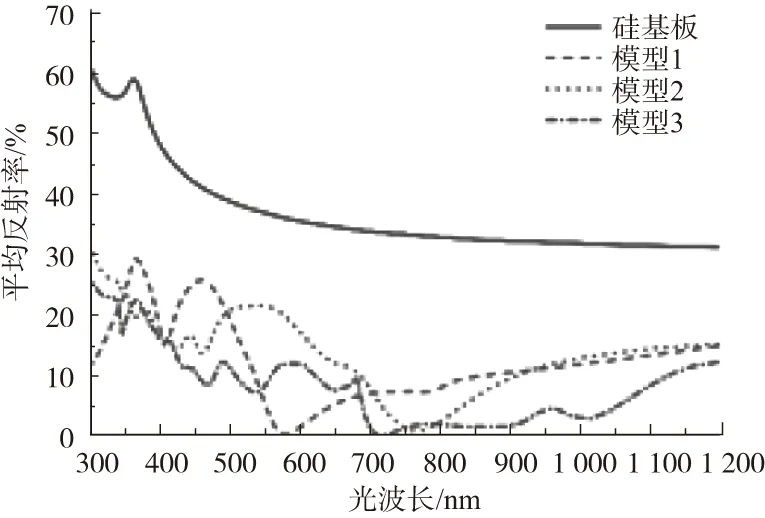
图3 模型1、模型2、模型3与硅基板的反射率图

对锥形阵列结构的高度Z进行研究，Z的取值范围为0nm～1500nm。图4表明随着纳米锥形阵列的高度提高，平均反射率不断下降，最终将平均反射率控制在10%左右。根据等效折射率理论，在其他参数不变的情况下，随着纳米锥阵列结构高度增加，结构的多层膜层数nt+1变大，导致相邻层面的折射率差值变小，结构的折射率渐变效果变得更好。但是随着纳米锥阵列结构的高宽比增大，需要精确地控制SF6与C4F8的气体比例以及刻蚀的时长。关键的技术难点在于纳米自组装的粒子既要能被去除，同时又要求去除粒子与硅基板的速率是可控的。

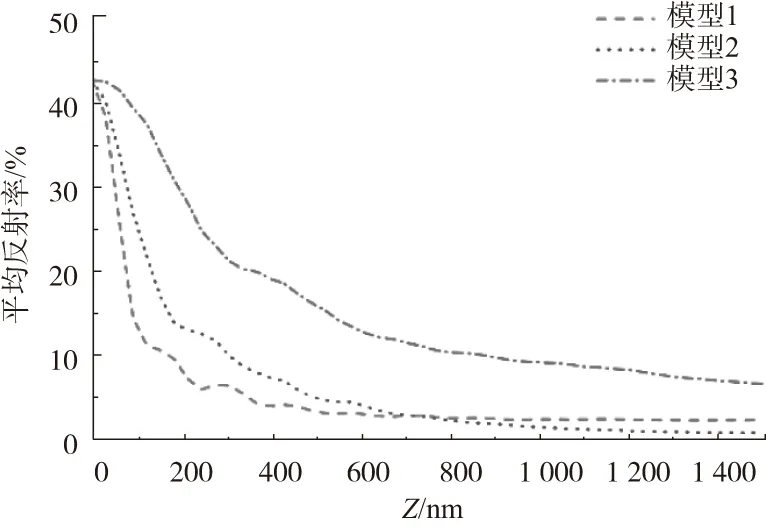
图4 阵列高度的反射率影响图

对底顶端直径Db进行分析，3个模型的Db如表2，模型1与模型2扫描范围起点为顶端阵列直径100nm处,模型3为300nm处，范围的终点值为对应结构的周期数值。如图5所示，仿真结果表明：随着底端直径增大，对应模型的平均反射率逐步降低，这表明锥形阵列结构要想达到较好的折射率渐变效果，就应该尽量地提高底端直径，直至占空比达到1.0。这给制造工艺提出了要求，制作抗反射的纳米锥形阵列时，当刻蚀到底端直径与结构周期相等时，就应停止刻蚀。

接下来对结构参数中的顶端直径Dt进行分析，Dt的取值范围如表2。从图6可以看出，随着顶端直径的增加，3个模型的反射率先减小后增大，在模型1、模型2、模型3中，Dt为125nm、175nm与100nm时平均反射率最小，说明此时的锥形阵列对于入射光的抗反射效果最佳。

图5 底端直径的反射率影响图

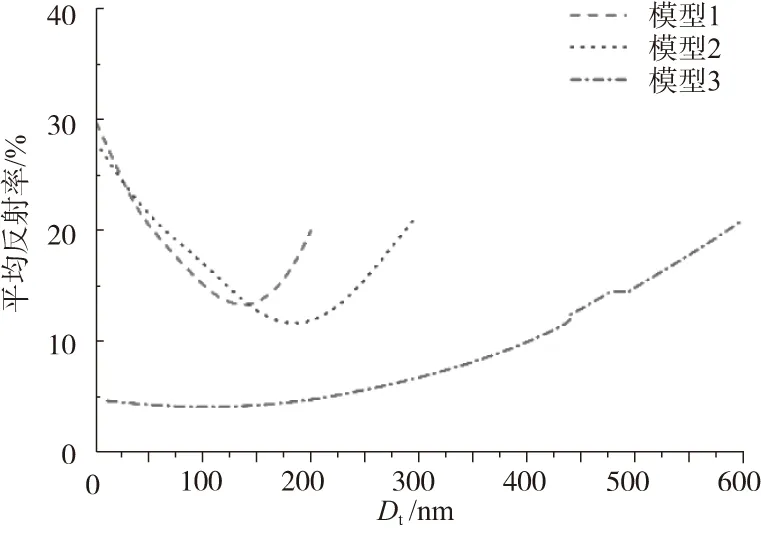
图6 顶端直径的反射率影响图

图7是对纳米锥形结构周期A的研究，结果表明随着周期A的不断增大，3个模型的平均反射率都是不断增加的。

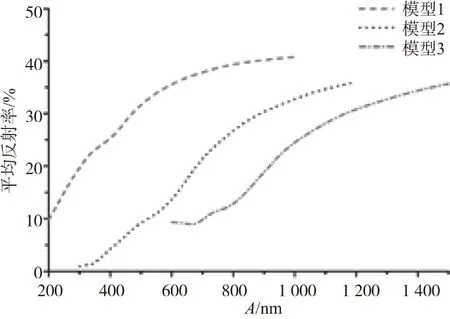
图7 阵列周期的反射率影响图

最后综合以上4个分析结果，找出每一个参数的较优解，将其带入仿真模型中建立如表3所示的3个优化后的锥形阵列结构模型参数，并进行仿真分析。由图7、图8可知，优化后模型1、模型2、模型3的平均透射率分别为3.89%、3.65%、1.34%。

表3 优化后锥形结构的模型参数 单位：nm

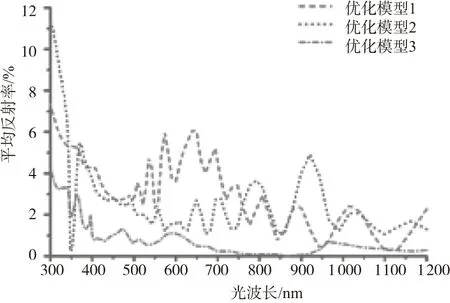
图8 3个优化后模型的反射率图

3 结语

为了提高硅基板太阳能的发电效率，克服实验的有穷性，探索硅锥形阵列结构的抗反射机理及规律，在实验的基础上进行FDTD仿真研究，得到硅纳米锥形阵列结构参数对平均透射率的影响规律。在光源为正入射的0.3μm～1.2μm的情况下，以波段内的平均透射率作为目标函数，对纳米锥形阵列结构参数进行了一系列的分析、仿真并得到规律：增加阵列高度、增加底端直径，减小阵列周期以及选择合适的顶端直径都可以降低平均反射率。优化后的模型1、模型2与模型3对比初始模型，其平均透射率分别下降了11.31%、13.75 %与11.50%；对比平整的硅基板平均透射率分别下降了39.40%、39.64%与41.95%。以上数据表明优化后的硅纳米锥形阵列结构能有效地降低平均反射率。