阵列旋转对功率倒置算法性能的影响分析

戴鑫志，李瑞丹，陈飞强，贾 珣

(1.北京卫星导航中心，北京 100081； 2.32022部队，武汉 430000； 3.国防科技大学，长沙 410005)

0 引言

面对日益拥挤的电磁频谱和复杂的电磁环境，卫星导航信号由于到达地面时功率非常微弱而极其容易受到各种有意或者无意的干扰，因此现代卫星导航接收机一般都会采取一定的抗干扰措施，以确保接收机在干扰环境下的生存能力。

阵列天线抗干扰由于对干扰类型不敏感、抗干扰能力强等优点，是目前导航接收机最有效的抗干扰措施之一[1]。决定阵列天线接收机抗干扰能力的关键之一是抗干扰算法，根据能否在期望信号方向形成增益，抗干扰算法可分为波束形成类和零陷类算法。波束形成类算法的代表是最小方差无失真响应(Minimum Variance Distortionless Respo-nse, MVDR)算法[2-3]和最小均方误差(Minimum Mean Square Error, MMSE)算法[4]等，能够在零陷干扰的同时在期望信号方向形成增益，但是算法实现时需要先验信息作为输入条件。零陷类算法的代表是功率倒置(Power Inversion, PI)算法[5-6]，PI算法能够在干扰方向上形成零陷，但不能对期望信号形成增益。不过由于PI算法不需要先验信息辅助、计算复杂度相对较小、易于工程实现等优点，在实际的阵列天线接收机中得到了大量的应用[7-8]，因此本文主要结合PI算法展开研究。

事实上除了抗干扰算法，阵列天线接收机的抗干扰能力还与阵列构型有关[9-10]，其内在机理是：阵列构型能够影响干扰信号与导航信号的空间相关系数，进而影响天线阵的抗干扰能力。其实，除了阵列构型，从空间相关系数的定义[11]可以看出，信号的来波方向也是影响空间相关系数的重要因素。文献[12]和文献[13]中已经发现，通过控制阵列旋转，可以降低干扰信号和导航信号的空间相关系数，提升抗干扰后输出信干噪比，但是没有进一步分析其内在机理并发现一般性的规律。总之，目前鲜有文章专门研究阵列旋转对PI算法抗干扰能力的影响，本文通过理论推导的方法建立了信号来波方向与PI算法抗干扰处理后阵列增益的关系，在此基础上，通过数值计算的方法分析了阵列增益随阵列旋转的变化规律，分析结果表明，通过阵列旋转能够改善PI算法的抗干扰性能。

1 阵列信号模型

不失一般性，假设天线阵阵元个数为N且第1个阵元作为参考阵元位于空间坐标系原点处。为便于理论分析，假设远场处有1个期望信号s(t)和1个干扰信号J(t)入射到天线阵,则天线阵的接收信号x(t)可表示为

x(t)=ass(t)+aJJ(t)+n

(1)

式中，as表示期望信号导向矢量;aJ表示干扰导向矢量;n表示方差为σ2的阵列通道噪声。信号导向矢量的定义[14]如下

(2)

其中，λ表示信号载波波长；zn,n=1,2,…,N表示一个3×1的指向阵元位置的矢量；d表示一个3×1的指向信号源位置的矢量。

假设干扰信号与期望信号不相关，因此接收信号的自相关矩阵Rxx为

Rxx=Rss+Rjj+σ2I

(3)

式中,Rss表示期望信号的自相关矩阵；Rjj表示干扰的相关矩阵；σ2I表示噪声的自相关矩阵，I表示一个单位矩阵。

天线阵抗干扰后，输出信号y(t)可表示为

y(t)=wHx(t)

(4)

式中，w表示阵列权矢量；[·]H表示共轭转置。

PI算法下，阵列权矢量由式(5)计算

(5)

(6)

式中，PJ表示干扰信号的功率。

将式(6)代入式(5)式,有

(7)

经过抗干扰处理后，期望信号输出为

ys=wHass(t)

(8)

其中，ρ表示干扰信号与期望信号的空间相关系数，其定义由式(9)给出

(9)

为便于比较阵列输出信号与单天线输出信号的差异，将式(5)中的权矢量w归一化,有

(10)

经阵列处理后，输出期望信号可表示为

(11)

则输出信噪比为

(12)

式中，ps表示单天线接收信号时的信号功率;pn表示噪声功率;|•|表示取模运算。而单天线接收信号时，输出信噪比为

(13)

利用式(12)和式(13)可得出阵列相较于单天线对期望信号的增益，即阵列增益为

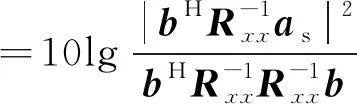
(14)

经过理论推导，有如下结果

(15)

(16)

因此有

(17)

式(17)即为PI算法下，天线阵对期望信号增益的具体表达式，它与抗干扰后输出载噪比的关系为

(18)

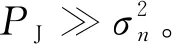
(19)

式(19)中虽然已经体现了PI算法抗干扰处理后阵列增益与空间相关系数的关系，但还没有建立阵列增益与信号来波方向的联系，因此还需要进一步分析。

2 阵列旋转对阵列增益影响分析

对常见的四阵元Y型阵列进行分析，其阵列构型如图1所示。

图1 四阵元Y型阵列模型Fig.1 Four-element Y-array pattern

假设导航信号和干扰信号的方位角和俯仰角信息分别为：(θs,φs)，(θJ,φJ)。由式(2)可得期望信号和干扰信号的导向矢量分别为

(20)

(21)

令导航信号与干扰信号在方位角上的间隔为Δ，即θJ=θs+Δ。由式(9)可得导航信号与干扰信号的空间相关系数为

(22)

假设天线阵在水平面内旋转，这意味着导航信号俯仰角φs、干扰信号俯仰角φJ以及方位角间隔Δ均不随阵列旋转而改变，式(22)中只有方位角θs会随着阵列旋转在[0,2π]范围内连续变化。保留变化量θs，将式(22)经过适当化简后，有

(23)

其中

(24)

进一步，由式(19)可以得到PI算法抗干扰处理后，阵列对导航信号的增益为

G=

(25)

式(25)形式比较复杂，但可以通过一些方法研究阵列增益G的一些性质。首先，通过式(25)中阵列增益的表达式不难得出：阵列增益G的取值受到方位角θs、导航信号俯仰角φs、干扰信号俯仰角φJ以及方位角间隔Δ这4个因素的影响。并且如果把阵列增益G看作一个函数G(θs)，则G(θs)是一个连续函数。

(26)

由于推导过程并不复杂，这里不给出详细的推导过程。当然，式(26)仅针对四阵元Y型阵列，不难得出对于其他具有几何对称性的天线阵，G(θs)将有其他的周期。

阵列增益G(θs)还有其他的一些性质，可以通过数值计算的方法得到。需要说明的是，G(θs)是一个连续的、周期性的函数，对于任意形状的天线阵都是成立的，其连续性可以通过复合函数的性质得到，周期性可以通过三角函数的性质得到。此外在理论分析过程中，均假设只存在一个干扰源，主要是考虑到对于多干扰存在时，数学表达式非常复杂，有的甚至难以用数学表达式描述。在后续的仿真实验中，将研究多个干扰源同时存在的情况。

3 数值分析

数值计算时，考虑到实际条件下干扰信号一般来自低仰角，而接收机进行定位解算时一般不取仰角过低的卫星，因此式(25)中可以取干扰俯仰角φJ∈[1°,15°]，信号俯仰角φs∈[10°,90°]，方位角θs∈[1°,360°]，方位角间隔Δ∈[0°,360°]。

取干扰信号俯仰角为5°，信号俯仰角为40°，天线阵旋转角度为360°，在方位角间隔分别为90°和150°时，利用式(25)画出阵列增益变化曲线如图2所示。

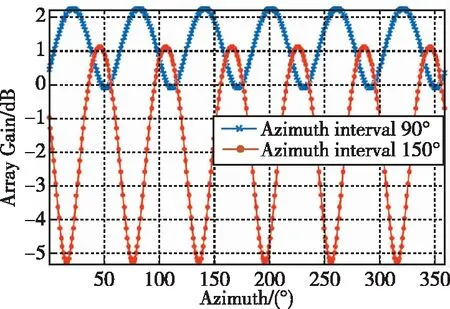
图2 阵列增益变化曲线Fig.2 Array gain curve

从图2可以看出，随着阵列旋转，不同方位角间隔下的阵列增益均以60°为周期连续变化，并且每个周期内，阵列增益存在一个最大值和一个最小值。通过计算机遍历所有的数值组合发现，得到的阵列增益随阵列旋转的变化曲线都是相似的，只是阵列增益波动的范围不同而已。由此可以得出G(θs)的另一个重要性质：在每个周期内，G(θs)存在一个最大值Gmax和一个最小值Gmin，最值的大小受到方位角间隔、导航信号俯仰角和干扰信号俯仰角的影响。

阵列增益曲线最大值Gmax与最小值Gmin之差Gmax-Gmin体现了阵列旋转时抗干扰输出载噪比的最大改善程度，也即对PI算法抗干扰性能的最佳改善程度。下面重点分析了阵列增益曲线中Gmax-Gmin的变化趋势。固定干扰信号俯仰角为5°，天线阵旋转角度为360°，方位角间隔从1°遍历至360°，导航信号俯仰角从10°遍历至90°，得到Gmax-Gmin值如图3所示。

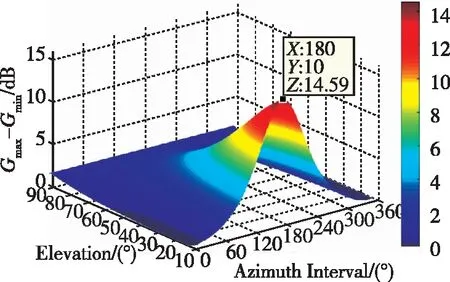
图3 阵列增益最大值与最小值之差变化 趋势(φJ=5°,φs=10°～90°)Fig.3 Difference between the maximum and minimum values of the array gain(φJ=5°,φs=10°～90°)

上述数值计算中干扰信号俯仰角φs保持不变，现令干扰俯仰角φJ从1°遍历至15°，由于得到的图像较多，这里不一一列出，仅给出干扰俯仰角为1°、10°和15°时的图像作为示例，如图4所示。

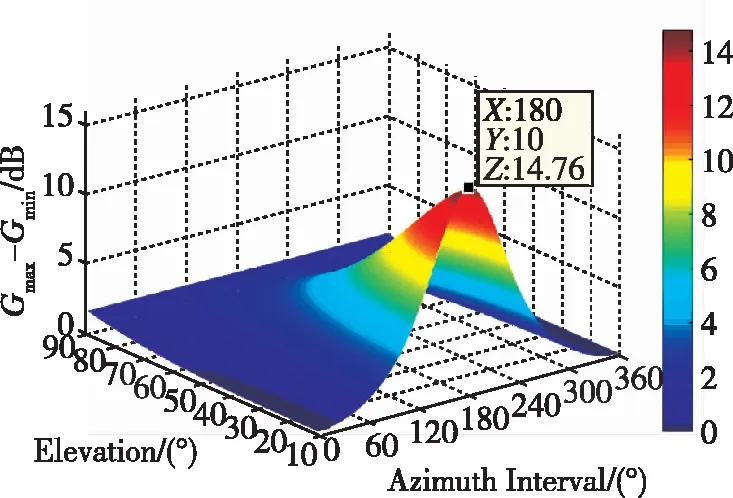
(a)φJ=1°

(b)φJ=10°

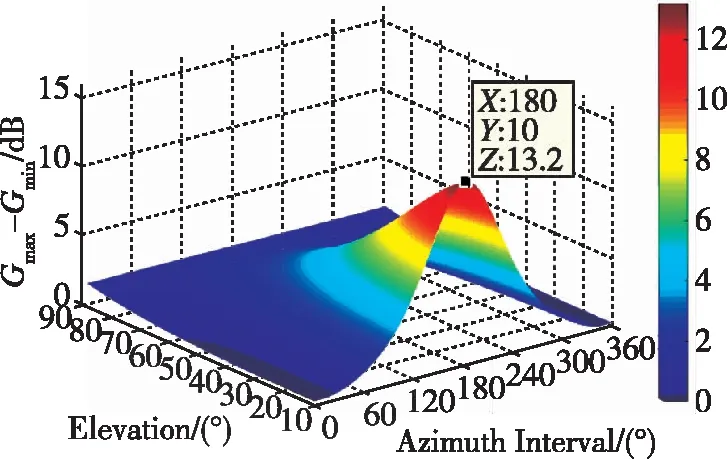
(c)φJ=15°图4 阵列增益极大值与极小值之差变化趋势(φs=10°～90°)Fig.4 Difference between the maximum and minimum values of the array gain(φs=10°～90°)

从图4中可以发现：Gmax-Gmin的变化趋势完全相同，不同干扰俯仰角下Gmax-Gmin最大值的差异仅有1dB左右，造成这一结果的原因是干扰俯仰角φJ变化范围较小(仅1°～15°)，因此对阵列增益的取值范围影响不大。此外，也可以发现，相同信号俯仰角条件下，Gmax-Gmin总是在方位角间隔180°左右取得最大值。综上，可以得出结论：在信号俯仰角越低、方位角间隔越靠近180°时，阵列旋转对阵列增益的改善程度越大，也即对PI算法抗干扰性能的提升越大。对于四阵元Y型阵列，在约束干扰来自低仰角、信号来自高仰角时，通过数值计算遍历所有来波方向可得，阵列旋转对抗干扰输出后载噪比的改善理论上最大可以达到14dB左右。

考虑一个位于水平面的天线阵，以一定的角速度在平面内匀速旋转，干扰源位置固定不变，或者相对天线阵以极小的角速度运动。由于导航卫星相对于地球运动的角速度很小，以GPS为例，GPS卫星运动角速度约0.0084(°)/s，因此在上述条件下可以认为卫星信号和干扰信号相对于旋转天线阵，其俯仰角在短时间内是不变的，而他们的方位角由于阵列旋转在[0,2π]内连续变化。

结合以上阵列增益G的性质可知，天线阵旋转时，方位角θs连续变化，阵列增益G会在Gmax和Gmin之间周期性变化，相比固定天线阵不变的阵列增益G0，由于Gmin≤G0≤Gmax，因此旋转天线阵能够在一段时间内获得更高的阵列增益(最大值附近)，即能够输出更高的载噪比，这意味着接收机将获得更佳的捕获性能。当然，阵列增益会随着天线阵旋转而周期性的变小，但由于导航接收机的跟踪灵敏度一般比捕获灵敏度低10dB左右[16]，因此只要信号被成功捕获并跟踪，载噪比减小时信号并不会轻易的失锁；即使信号失锁，信号失锁后重捕的难度也远小于直接捕获的难度。因此从信号捕获效果看，阵列旋转能够改善接收机的信号捕获性能。

关于天线阵旋转角速度，主要考虑2个约束因素，一方面要保证阵列增益在极大值附近时，接收机有足够的数据实现捕获跟踪，因此角速度不能过快；另一方面，旋转角速度也不能过慢，因为旋转过慢会导致阵列增益变化缓慢，延长信号捕获时间。阵列旋转角速度需要考虑上述2个因素，并结合接收机的实际性能和使用需求进行选择。

4 实验验证

为了验证理论分析和数值计算的正确性，使用软件接收机进行仿真。仿真中，天线阵使用四阵元Y型阵列，阵元间距半波长，导航信号使用北斗B3民码信号，信噪比为-20dB，干扰为20M带宽的高斯白噪声干扰，干信比为70dB，天线阵以1(°)/s的角速度进行旋转。不同的时间段，干扰信号和导航信号随机选择不同的来波方向，如表1所示。

表1 干扰信号及导航信号来波方向

经过PI算法抗干扰处理后，实际阵列增益与利用式(22)计算的理论阵列增益对此如图5所示。

图5 阵列增益仿真值与理论值对比Fig.5 Comparison of the simulation and the theoretical value of array gain

从图5可以看出，不同来波方向下，仿真阵列增益均与理论阵列增益保持一致，证明了理论推导的正确性。鉴于理论推导和数值计算仅分析了单干扰的情况，利用仿真研究了多干扰条件下阵列增益随阵列旋转的变化规律。

对于双干扰情况，假设环境中存在一个GNSS信号，信噪比为-20dB，还存在一个高斯宽带干扰和一个连续波干扰，干信比均为70dB，天线阵以1(°)/s的角速度旋转。不同的时间段，干扰信号和导航信号随机选择不同的来波方向，如表2所示。

表2 双干扰条件下信号来波方向

经过PI算法抗干扰处理后，阵列增益的仿真结果如图6所示。

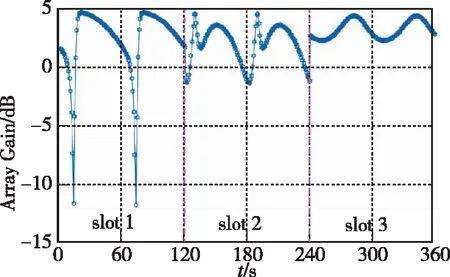
图6 双干扰存在条件下的阵列增益Fig.6 Array gain in the presence of two interfering signals

从图6可以看出，双干扰存在条件下，阵列增益变化曲线与单干扰条件下的变化曲线明显不同。例如双干扰条件下，增益变化曲线的极值点与最大值和最小值点并不一定重合；其次，对于不同的来波方向，曲线的变化形式也有较大的差异。但可以发现，随着阵列旋转，阵列增益仍然以60°为周期在最大值和最小值之间连续变化，在不同的时段，阵列增益的最大值与最小值之差分别为15dB、5dB和2dB。

在双干扰仿真的基础上，增加一个高斯窄带干扰，使仿真环境中存在3个干扰。不同的时间段，干扰信号和期望信号的来波方向，如表3所示。

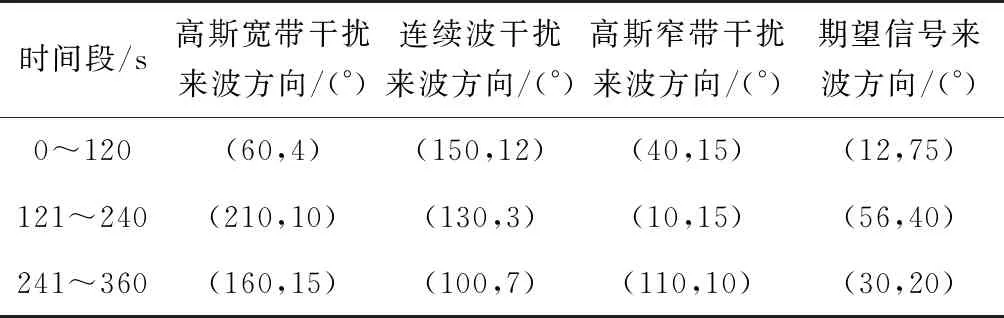
表3 三干扰条件下信号来波方向

经过PI算法抗干扰处理后，阵列增益的仿真结果如图7所示。

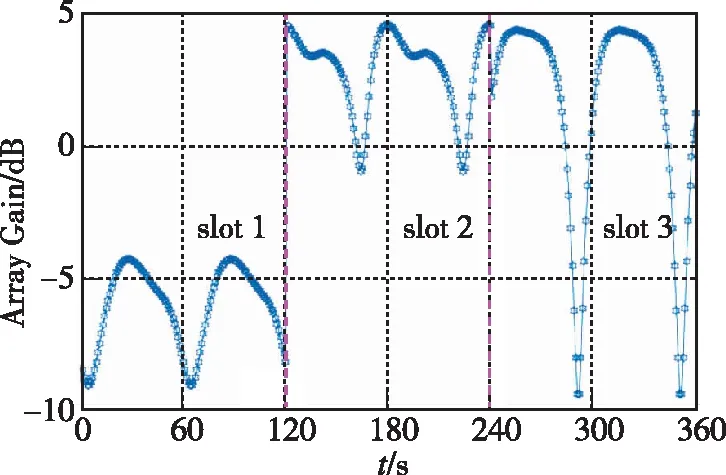
图7 三干扰存在条件下的阵列增益Fig.7 Array gain in the presence of three interfering signals

从图7可以看出，三干扰条件下，阵列增益仍然以60°为周期在最大值和最小值之间连续变化，在不同时段，阵列增益的最大与最小值之差分别为4dB、5dB和14dB。

以上仿真结果说明，在存在多干扰条件下，旋转天线阵仍然可以改善阵列对卫星信号的增益，提升抗干扰输出后的载噪比。

5 结论

本文以阵列天线接收机中常用的PI算法为研究对象，通过理论推导的方法研究了信号来波方向与阵列增益的关系，并在此基础上分析了阵列增益随阵列旋转的变化规律。分析结果表明，PI算法下阵列增益受到干扰和导航信号来波方向的影响，相比于固定天线阵，阵列旋转可提升阵列增益，意味着阵列旋转可改善输出载噪比，并提升接收机捕获性能。仿真结果证明了理论和数值分析的正确性，并进一步证明了在多干扰存在的条件下，阵列旋转仍可得到相似结论。该研究成果对设计更高性能的卫星导航功率倒置阵具有一定的参考及借鉴价值。