卫星拒止情况下低精度惯导系统航姿算法研究
2021-02-03蒋海涛管春洋申争光
蒋海涛, 辛 吉, 管春洋,申争光
(1.海装驻北京地区第三军事代表室,北京 100074; 2.空装驻北京地区第二军事代表室,北京 100074; 3.北京自动化控制设备研究所,北京 100074)
0 引言
随着导航技术和微加工技术的发展,微机电系统(Micro-Electro-Mechanical System,MEMS)惯性器件与卫星导航、磁航向计和气压高度计等组成的导航系统,广泛应用于低成本军用飞行器和商用飞行器。在电磁环境复杂、卫星干扰强烈的使用场景中,例如军事要地、重要工业区域和复杂地形环境下,卫星导航辅助的低精度惯导系统往往会失效。无卫星辅助的情况下,低精度惯导系统的水平姿态随时间发散较快,进而会造成飞行器控制系统失稳失控。
在卫星拒止的情况下,低精度惯导系统如何利用惯性器件信息和飞行器的动力学模型保持水平姿态精度是当今学者研究的重点方向。文献[1]提出了一种低成本高精度航姿系统,通过扩展Kalman滤波进行数据融合以获得姿态的准确输出,姿态角动态精度优于2°。文献[2]提出了利用运动状态判别,根据运动状态采用不同的量测值进行Kalman滤波以估计姿态误差角,从而提高航向姿态精度。文献[3]设计了由3个微陀螺仪、3个微加速度计和3个微磁航向计组成的航姿参考系统,利用加速度计对磁航向计数据进行正交化处理,并利用基于最小二乘法的椭球拟合校正方法对测量数据进行校正。文献[4]研究了基于磁航向计的航姿测量系统误差补偿。由于磁航向计体积小、成本低,在商业级和娱乐级飞行器中使用广泛[5]。而在军事领域,由于任务区的电磁环境复杂,受到环境磁场以及载体的硬铁磁场和软铁磁场的影响,磁航向计测量值误差大,不能作为可靠稳定的传感器。
针对巡飞型飞行器的飞行特点,本文基于重力矢量和载体的动力学特性,提出了一种基于动态检测和Kalman数据融合[6-8]的航姿算法[9-10]。本算法中航向角和姿态角根据三轴陀螺仪数据进行实时更新,经过动态判断和飞控状态判断,Kalman滤波器对水平加速度数据进行数据融合,并在低动态情况下进行量测更新,以修正水平姿态误差。
1 低精度惯性导航的航姿算法研究
低精度的惯性导航系统的陀螺漂移通常大于40(°)/h,加速度计零位误差大于2mg。由于陀螺漂移误差大,水平姿态角采用传统姿态角解算方法发散较快。本文采用Kalman滤波方式,利用水平加速度计测量值为观测量,对水平姿态角误差进行估计和修正。本方法的原理与惯导自对准计算水平姿态角的原理相同[11-13],当载体晃动即存在有害加速度(载体加速、转弯引起的向心加速度)时,水平姿态角误差较大,且姿态误差与有害加速度的大小正相关。
1.1 惯性导航自主对准原理
惯导自对准的计算采用直接解析法,即通过矩阵运算直接求解出载体的姿态。在静态情况下,采用重力矢量g、地球自转矢量w和2个向量的叉乘V计算载体坐标系相对于导航坐标系的姿态矩阵[14]
(1)
(2)
式中,gb为载体坐标系下的加速度;wb为载体坐标系下的角速度;Vb=gb×wb。
(3)
为降低传感器高频噪声及高频环境晃动的影响,加速度和角速度需要取一段时间的均值进行计算。
对准误差的分析参见文献[15],在此直接给出分析结论
(4)
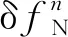
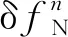
1.2 航姿模式Kalman滤波器设计
根据航姿系统的特点,Kalman滤波器的系统状态方程采用3个失准角误差和3个陀螺漂移误差共六维,观测方程采用水平加速度计的测量值,其中状态方程定义如下
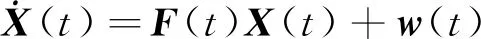
(5)
式中,F(t) 为t时刻连续状态方程系统矩阵;w(t)为t时刻系统随机噪声向量。
根据Kalman滤波状态量建立系统误差模型,建立系统方程如下
(6)
即F(t)中非零元素如下
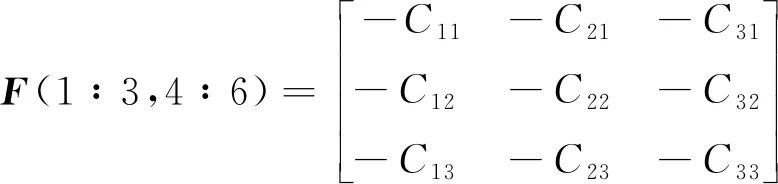

状态变量定义如下
X=[φNφUφEεxεyεz]T
其中:X为Kalman滤波估计状态量;φN、φU、φE、εx、εy、εz分别为北向失准角、天向失准角、东向失准角、X陀螺漂移、Y陀螺漂移和Z陀螺漂移。
当系统处于低动态时,加速度计测量值主要为重力矢量,而2个水平方向的分量几乎为0,因此有以下关系式成立
(7)
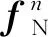
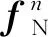
H为测量矩阵
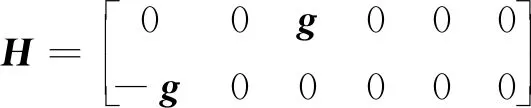
式中,g为当地重力加速度。
1.3 滤波流程
滤波过程中,每对陀螺和加速度计进行一次采样即计算一次系统转移矩阵,并根据滤波周期对系统矩阵进行离散化,如下所示
(8)
Φk,k-1=Fsum
式中,Tn为惯性导航周期,此处为0.005s。离散化完成后对Fsum清零。
连续系统离散化以后为离散系统,离散系统的模型方程为
(9)
1.4 航姿模式反馈修正算法
Kalman滤波器估计出水平失准角后,对水平姿态角进行误差补偿,为保证输出水平姿态的平稳性,对修正值进行限幅,采用固定周期(1s)修正的方式。
当满足水平失准角修正条件后,同时修正2个水平失准角,修正量限幅为φLimit°。记修正量分别为φN和φE
(10)
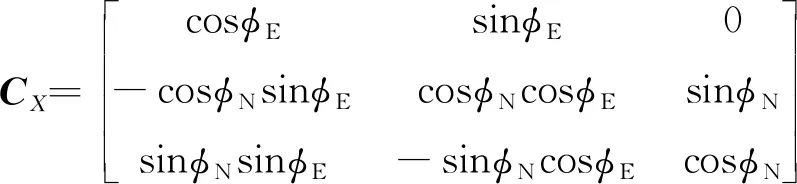
(11)
修正后,从Xk中对应元素扣掉修正值
X1=X1-φNX3=X3-φE
式中,X1和X3分别为Kalman滤波估计状态量X的第1项(北向失准角φN)和第3项(东向失准角φE)。
2 飞行器动态检测
飞控模块根据目前的控制指令发送给航姿系统当前飞行器的飞行状态。在飞控模块发送平飞状态时,受到结构干扰、推阻不匹配和风力等影响,飞行器可能处于侧滑或小角度转弯等飞行状态,因此需要利用惯测信息进行低动态判断。低动态的判断门限跟载体的飞行状态、转弯特性和控制品质密切相关。根据低空固定翼飞行器的飞行特点和动力学特性,低动态需要同时满足以下3个条件:
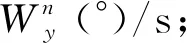
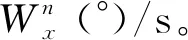
选用一组具有转弯和直航的飞行试验数据如图1所示,对低动态判断进行分析。根据动态情况判断,在飞行器航向机动时,首先进行滚转,通过X向角速度1s均值(见图2)的门限2(°)/s,可以先于Y向角速度和合加速度判断出航向机动,但是X向角速度仅在机动的前段和后段;通过Y轴角速度1s均值(见图3)的门限0.5(°)/s,可以判断出航向存在持续性的转动,作为X向角速度判断的延续;合加速度的门限(见图4)0.2m/s2作为Y轴角速度判断的补充,不仅可以判断出存在航向机动时的向心加速度,还可以判断出纵向和天向的加速状态。3个量联合使用可以确保载体处于低动态飞行状态。
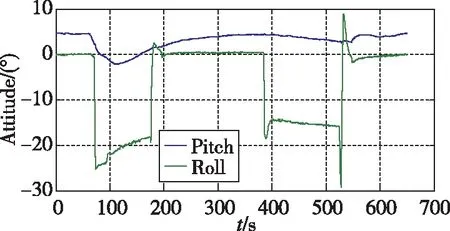
图1 飞行器飞行姿态Fig.1 Attitude of the aircraft
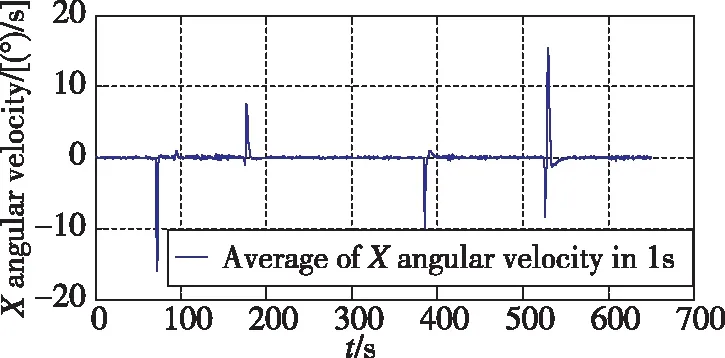
图2 X向角速度1s均值(门限Fig.2 Average of X angular velocity in 1s(threshold
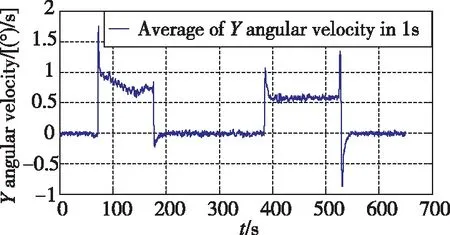
图3 Y向角速度1s均值(门限Fig.3 Average of Y angular velocity in 1s(threshold
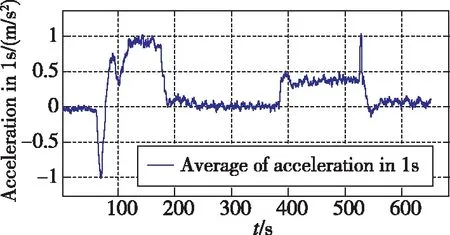
图4 合加速度1s均值(门限Fig.4 Average of acceleration in 1s(threshold
3 仿真验证
根据上述算法和策略,利用实际飞行数据进行离线仿真,飞行器为固定翼巡飞器,采用小型涡扇发动机,任务半径100km。下面绘制曲线均为进入航姿模式后系统输出的结果,误差的比较基准为实际飞行的惯性卫星组合导航结果。三轴陀螺漂移约为40(°)/h,加速度计零位约为2mg。
滤波参数设置如下
P0=diag{(5°)2,(15°)2,(5°)2,(200°/3600s)2, (200°/3600s)2,(200°/3600s)2}
Q=diag{(40°/3600s)2,(40°/3600s)2,(40°/3600s)2, (5°/3600s)2,(5°/3600s)2,(5°/3600s)2}
R=diag{(0.1m/s2)2,(0.1m/s2)2}
飞行器的飞行轨迹为U形轨迹如图5所示,航向角和水平姿态曲线分别如图6和图1所示。飞行器处于低动态情况下(根据低动态判断结果),在直飞段可以利用航姿滤波器进行水平失准角修正。航向角由于缺乏航向传感器(磁航向计、双天线卫星导航接收机等)的辅助,依靠航向陀螺精度保证航向角的准确性。航向陀螺设为40(°)/h,导航600s的航向角误差约为6.7°,能够满足飞行器稳定控制飞行的要求。若飞行器中存在精度较高且可靠的航向角信息,可以对航向角进行进一步修正,以保证航向角的精度。
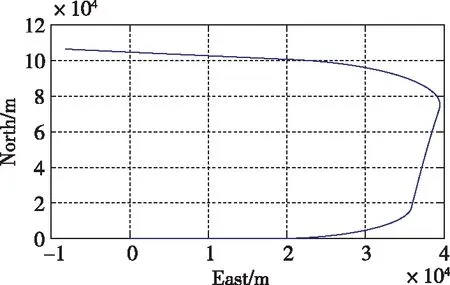
图5 飞行轨迹Fig.5 Flight path
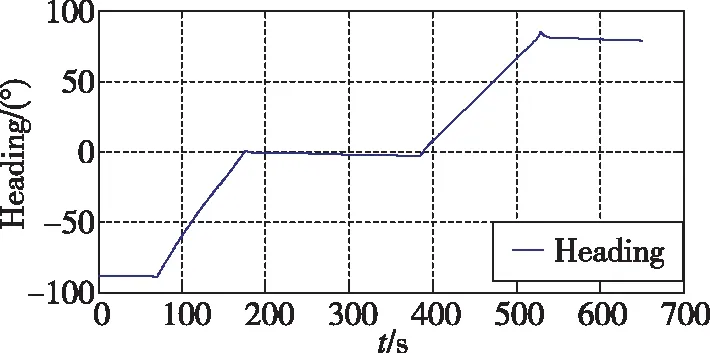
图6 飞行器飞行航向角Fig.6 Heading angle of the aircraft
当导航模式未采用航姿算法时,水平姿态采用惯性解算的方式,随时间发散较快如图7所示,无法维持飞行器长时间稳态飞行。当导航模式采用航姿算法时,飞行器在直飞段的飞行动态满足低动态判断门限,航姿滤波器利用水平加速度计的信息进行滤波,滤波收敛后反馈校正水平姿态,水平姿态误差快速变小至零附近,如图8所示;飞行器进入转弯段则不满足低动态判断门限,航姿滤波器不进行量测更新只进行时间更新,水平姿态误差不进行反馈校正,水平姿态误差发散趋势与纯惯性状态一致,水平姿态误差如图8所示。航姿模式计数和修正次数计数如图9所示,在低动态情况下,航姿模式计数每1s累加1次,非低动态情况下航姿模式计数维持不变。在航姿模式下,当姿态角每修正1次时,修正计数累加1次,非航姿模式时清零。结合图8和图9可以看出,在航姿模式下,随着修正次数的累加,东向和北向失准角误差逐渐变小,滤波器估计的水平失准角准确。
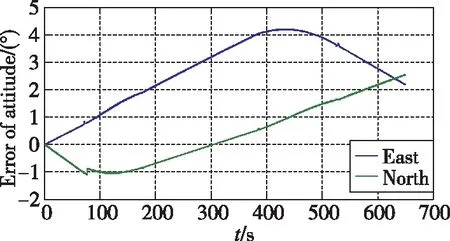
图7 无航姿模式辅助情况下水平姿态角误差Fig.7 Attitude error without the assist of attitude and heading reference
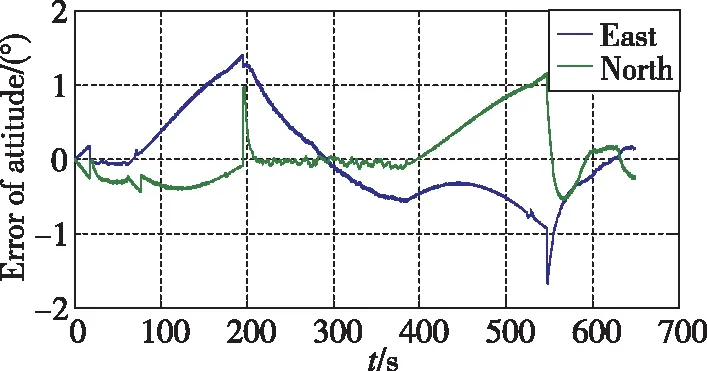
图8 航姿模式辅助情况水平姿态角误差Fig.8 Attitude error with the assist of attitude and heading reference
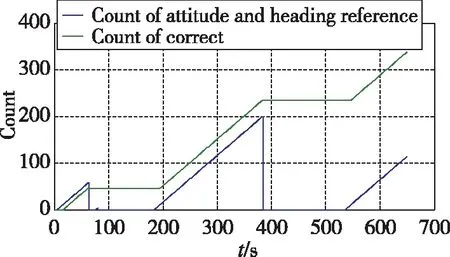
图9 航姿模式计数累计值Fig.9 Count of attitude and heading reference
4 结论
在卫星拒止情况下,低精度惯导系统利用航姿算法可以维持水平姿态在较高的精度,满足飞行器的飞行控制要求。
1)本文的航姿算法是一种适用于低空巡飞型固定翼无人机和旋翼型无人机等装备的低成本惯导系统在卫星拒止情况下的航向姿态计算方法。
2)本文利用机动状态判断和飞控指令相结合的方式,采用六维状态方程和二维观测方程的Kalman滤波器估计和修正水平失准角,水平姿态误差可控制在2°以内。
