面向结构化场景的激光雷达点云高精度配准与定位方法
2021-02-03何洪磊赖际舟向林浩李志敏
何洪磊,赖际舟,吕 品,向林浩,李志敏
(1.南京航空航天大学,南京 211106; 2.中国船级社,北京 100007)
0 引言
近年来,随着科技的进步,机器人行业得以快速发展,无人设备在巡检、运输等领域扮演着重要角色。同时为了完成愈加复杂的工作任务,人们对其定位导航能力也提出了更高的行业要求。在该过程中,激光雷达凭借测距精度高、感知能力强等特点逐渐成为卫星拒止环境下无人设备的主要导航传感器之一。
针对机器人的室内导航问题,当前工程上主流的导航方案为:首先通过多源信息融合算法构建高精度激光点云地图[1-3],随后将无人设备实时激光雷达数据与构建的先验地图进行匹配,从而获得机体位姿。该过程首先需将雷达系与地图系对齐,实现机体位姿初始化,因此需要通过点云粗配准[4-5]的方法进行机体的初始定位。点云配准分为特征提取与位姿解算两部分,Dong Z.等提出了在算法前端采用基于局部特征描述[6-9]的点云特征提取方法建立点云关联,如三维形状上下文、点特征直方图、快速点特征直方图等,该类方法通常适用于特征丰富的小场景,但在大型的结构化场景下该类特征区分度较低,导致特征关联的错误率较高。Zhang X.等提出了基于概率统计的多元正态分布变换(Normal Distributions Transform, NDT)[10],建立了两帧点云之间的关联,然而受限于特征配准的收敛性,该方法不适用于位姿差异过大的两帧点云。上述两种方法均采用基于迭代的位姿解算方法,计算量较大,并且在大型结构化场景的点云配准过程中易陷入局部最优[11],从而产生错误的导航解算。
因此在结构化环境中,需要一种鲁棒的特征提取方法,S.Ochmann和S.Oesau等提出了空间结构的平面模型化表示方法[12-13],可以从三维点云中恢复建筑物的空间环境结构。在大型结构化场景中,该类特征具有一定鲁棒性,然而该类算法复杂度较高,同时利用该类特征进行无人系统初始定位的方法还未见文献报道。
基于此,本文提出了一种基于多平面空间模型的激光雷达点云配准方法。首先对传统空间结构恢复方法进行改进,采用优化特征直方图[14]实现了空间平面的快速分割与拟合,以及大型结构化空间环境的模型化表示。随后为了避免解算过程中的局部最优问题,不同于传统算法中基于迭代的位姿求解方法,本文算法采用空间平面线性匹配方式实现两帧点云面特征的快速配准,提高了计算效率。
1 基于多平面模型的面特征快速提取方法
三维激光雷达点云数据量庞大,所以需要通过特征提取的方式建立两帧点云之间的关联。传统方法对特征的数量要求大,增加了算法的整体计算负担,且在特征稀疏或特征区分度较小的环境中,难以保证算法的特征精度。针对该问题,本文利用结构化环境特点,采用优化的特征直方图思想实现了空间点云的快速分割聚类,并根据平面一致性对点集进行合并,最终实现了高效、鲁棒空间面特征的提取。
1.1 基于特征直方图的三维点云快速分割方法
首先,根据李新春等[15]提出的方法对滤波后激光雷达点云的法线nk进行计算
(1)
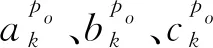
不同于传统的特征提取算法(如FPFH),本文算法采用平面作为点云特征,考虑到法向量相同的点可以近似为同一个平面点,采用优化的特征直方图对法线特征进行快速分析,以实现点云的粗聚类。将点云法线的三维特征区间asec、bsec、csec分别等分为m个特征区间,并排列组合形成m×m×m个三维特征区间,最终构建出法线特征直方图(见图1)。
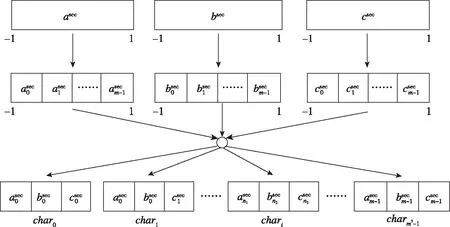
图1 基于特征直方图的特征区间划分方法Fig.1 Feature interval partitioning method based on feature histograms
第i个特征chari表示的特征区间为
(2)
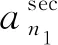
(3)
将点云根据其法向量特征的数值投放到不同的特征区间,形成激光雷达三维扫描特征直方图,从而实现三维点云的快速粗分割。
1.2 基于平面一致性的点集合并及平面拟合方法
在式(3)中,当阈值m选取较大时,chari的特征空间较小,同一平面点云易被分割成多个部分。因此,点云快速粗分割后,需根据平面一致性将同一平面但不同特征区间的点云进行合并。
选取数据量最大的λ组特征区间内的点云进行粗拟合,归一化后可得平面方程
(4)
其中,t为chari内点云数据量;d为方程归一化常数。
(5)
(6)
则根据式(5)计算两法线向量pi和pj之间的偏差eij。当eij≤δ时,将两特征区间内的点云数据合并。根据设定的空间模型平面数量,保留点云数据量最大的k组点云。最后采用随机抽样一致性(Random Sample Consensus, RANSAC)算法去除各组点云离群点以提高平面鲁棒性,并将滤波后的平面点云拟合生成k个平面,形成平面方程的形式如式(7)
(7)
2 基于多平面模型的特征快速配准方法
假设机体为刚体,所有的运动变换均为刚体变换,则可利用两帧点云之间的特征关联建立位姿优化函数,从而求取位姿变换最优解。传统算法采用基于迭代的目标函数优化方法,然而该方法计算量较大,并且当特征精度较差或环境特征区分度较低时,迭代算法易陷入局部最优。因此,本文基于线性最小二乘对面特征进行配准。首先通过空间平面排序建立两帧点云的面特征关联,而后通过线性最小二乘实现平面的快速配准,使得算法在提高计算效率的同时避免陷入局部最优。
2.1 基于排序的特征关联方法
当雷达点云与地图点云分别拟合出k个平面后,需要建立两帧点云平面间的特征关联。然而若两帧点云平面是无序的,随机关联平面特征,则其后续计算的时间复杂度为O((k-1)!n);若两帧点云平面是有序的,则其后续计算的时间复杂度为O((k-1)n)。因此,为了提高计算效率,对点云平面进行排序。
首先求取点云平面与XOY平面交线
(8)

(9)
式中
(10)
如图2所示,若空间平面模型与XOY平面相交为6条直线,根据式(9)和式(10)计算可得
gl6>gl4>gl1>gl3>gl5>gl2
(11)
将平面按照位置分数从大到小的顺序排序,即可实现平面的逆时针有序排列。

图2 空间平面快速排序方法Fig.2 Spatial plane quicksort method
2.2 基于线性最小二乘的配准快速解算方法
通过两帧点云的面特征关联,可形成k-1组有效平面约束。定义第i组对应平面的平面系数为(ai,1,bi,1,ci,1)与(ai,2,bi,2,ci,2)。选取待求解变量tx、ty、θ,其平面系数的转换关系如式(12)
[-ai,1-bi,1ci,2-ci,1]T=
(12)
其中,tx、ty、θ分别表示两帧点云之间的水平位置差及航向角偏差。传统基于迭代的目标函数解算方法计算量较大且易陷入局部最优。为了避免该问题,本文采用线性求解的思路进行解算
ai,2ci,1tx+bi,2ci,1ty=ci,2-ci,1
(13)
若空间平面中所有平面均垂直于地面,则式(13)为恒等式。因此,构建待优化函数如式(14)
(14)
式中
(15)
采用最小二乘拟合算法进行解算,可得
Aξ=B
(16)
式中
(17)
(18)
(19)
式(17)中
(20)
2.3 平面配准的最优解选定方法
两帧点云的点云平面均逆时针排列后,一共可产生k-1种面特征关联情形。首先通过预置区域Φ对位姿解算结果进行粗筛选,并定义误差函数ek对其配准度作进一步分析,从而提取最优解
(21)
(22)
式中
(23)
(24)
将配准结果经过式(21)和式 (22)解算后,保留误差最小解即为两帧点云配准的最优解。
3 实验验证及分析
本文分别通过Gazebo仿真与室内结构化场景模拟实验对算法进行验证与分析。采样一致性初始配准(Sample Consensus Initial Alignment, SAC-IA)与迭代最近点(Iterative Closest Point, ICP)算法是当前主流的点云配准算法,因此,将本文算法与SAC-IA算法及SAC+ICP组合算法的点云配准结果进行对比分析。
3.1 Gazebo仿真验证与分析
仿真平台采用Gazebo机器人仿真系统,Gazebo是一款三维动力学仿真软件,软件内置物理引擎,能够对环境、无人系统、传感器进行高保真的物理模拟。船舱的近观检验[16]是保障船舶安全航行的重要手段,采用无人机取代人工进行船舱检验具有重大的经济效益。因此,在Gazebo中根据船舱真实环境构建如图3所示仿真模型,以验证算法的有效性,同时在仿真环境中加入障碍物以验证算法的可靠性。

图3 仿真环境模型Fig.3 Simulation environment
Gazebo构建无人系统包括:
1) hector quad rotor微小型飞行器载体,机体实时发布位姿真值,以对本文算法进行性能评估;
2)机载16线三维激光雷达,水平角分辨率0.3°、垂直角分辨率2°,水平视场360°、垂直视场±15°,测距误差±2cm,测距范围0~100m;
数据处理计算机采用Linux(Ubuntu 16.04)的机器人操作系统(Robot Operating System, ROS),处理器为G2020,主频2.9GHz。
仿真数据采集点如图4所指示。其中,P0表示地图构建原点,Pi表示激光雷达数据采集点,各点箭头表示雷达在该点处x轴指向,黑色方块表示障碍物位置及其姿态。
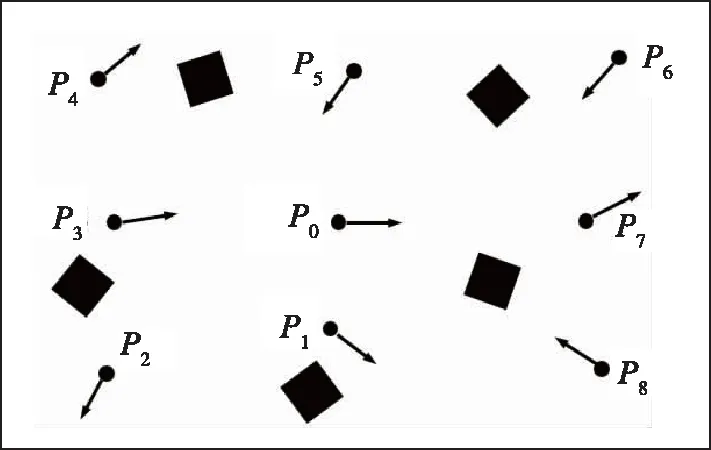
图4 仿真数据采集点示意图Fig.4 Simulation data acquisition point
(1)地图点云预处理
首先对地图点云(如图5(a)所示)进行处理。在位姿初始化过程中,仅有邻近地面的点云参与解算,所以根据高度值对地图点云进行截取(如图5(b)所示)。仿真环境相对结构化,噪点较少,故设定特征区间数量m为7,保留平面数量k为5,通过本文算法对地图点云进行平面分割(如图5(c)所示)。由图可见,本文算法对地图点云进行了较为精准的快速分割,并自动滤除障碍物点。
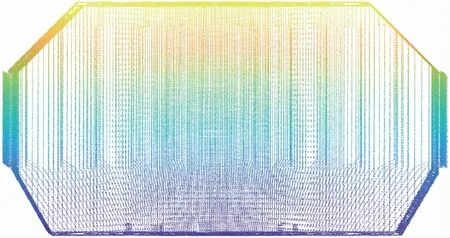
(a)地图点云

(b)截取后地图点云

(c)地图点云分割图5 地图点云预处理Fig.5 Map point cloud preprocessing
以激光雷达地图点云为目标点云,Pi各点采集到的激光雷达点云为输入点云,进行点云配准实验。
(2)配准精度对比分析
输入点云与目标点云如表1所示,其中,绿色点云为目标点云,红色点云为输入点云。
从表1中可以看出,即使有障碍物,本文算法对三维空间点云仍然可以进行较为精准的分割,实现了空间结构的模型化处理。
点云配准后解算位姿与各点位姿参考值如表2所示。
从位置1、2、3、4点云的配准情况以及定位结果分析可以看出,SAC-IA算法的定位精度为米级,航向角平均偏差在2°以上,存在较大误差;而本文算法定位偏差均小于0.1m,航向角偏差小于0.5°,与SAC +ICP组合算法的全局最优解具有相当的精度等级。同时这也表明了本文算法中通过大数据点云聚类拟合的面特征具有较高的精度与可靠性。

表1 点云配准对比Tab.1 Point cloud registration comparison

表2 位置1~4点云配准精度对比Tab.2 Comparison of cloud registration accuracy at position 1~4
传统算法在解算位置5、6、7、8处位姿的过程中,产生了错误解算(如表3所示)。这表明传统算法在特征区分度较小的大场景空间环境中容易产生局部最优问题。而在该情况下,本文算法依旧保持了较高的定位精度。

表3 位置5~8点云配准精度对比
(3)计算效率对比分析
本文算法与SAC-IA算法计算时间统计如表4所示。
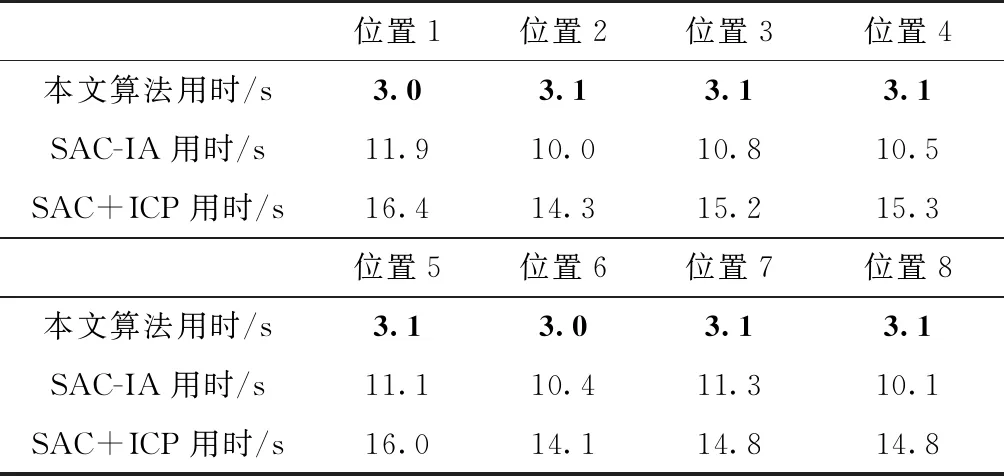
表4 计算效率对比Tab.4 Computational efficiency comparison
由表4可得,本文算法的平均用时为3.1s,SAC-IA算法的平均用时为10.8s,SAC+ICP算法的平均用时为15.1s。所以在仿真实验中,本文算法的计算效率约是SAC-IA算法的3.5倍,是SAC +ICP算法的5倍。相较于传统算法,本文算法减少了特征提取的数量,在位姿求解过程中,本文算法使用线性最小二乘算法取代了传统算法位姿解算中采用的非线性最小二乘算法,无需迭代求取最优解,从而提高了计算效率。
3.2 室内结构化场景模拟试验验证
实验环境及实验器材如图6所示。

图6 实验环境Fig.6 Experimental environment
实验器材包括:
1)8个高速摄像头组成的动态捕捉系统,为本文实验提供位姿基准(cm级精度);
2)VLP-16三维激光雷达。
计算平台与仿真实验相同。实验设计如图7示。
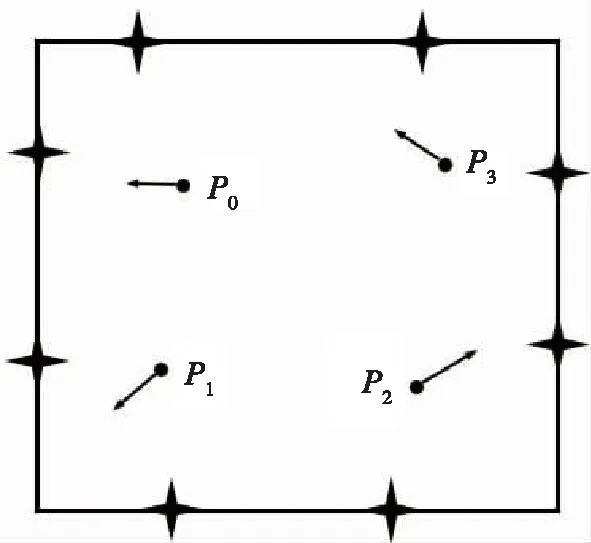
图7 数据采集示意图Fig.7 Data acquisition point
其中,P0表示地图构建原点,Pi表示激光雷达数据采集点,各点箭头表示雷达在该点处x轴指向,黑色十字星表示动态捕捉系统的高速摄像头位置。
(1) 地图点云预处理
构建的实验环境地图如图8所示。
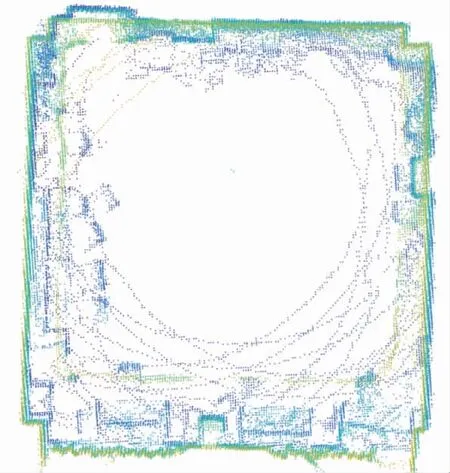
图8 地图点云Fig.8 Map point cloud
由于室内环境噪点较多且点云中地面点较少,适当调大特征区间数量m,将其设定为10,保留平面数量k为4,通过本文算法对地图点云进行平面分割(如图9所示)。由图9可见,在实际环境中,本文算法对点云进行了较为精准的分割。

(a)分割后地图点云

(b)分割点云俯视图图9 地图点云预处理Fig.9 Map point cloud preprocessing
(2)配准精度对比分析
传统算法的点云配准结果与本文算法的点云分割及配准结果如表5所示,其中,绿色点云为地图点云,红色点云为各点位的数据采集点云。
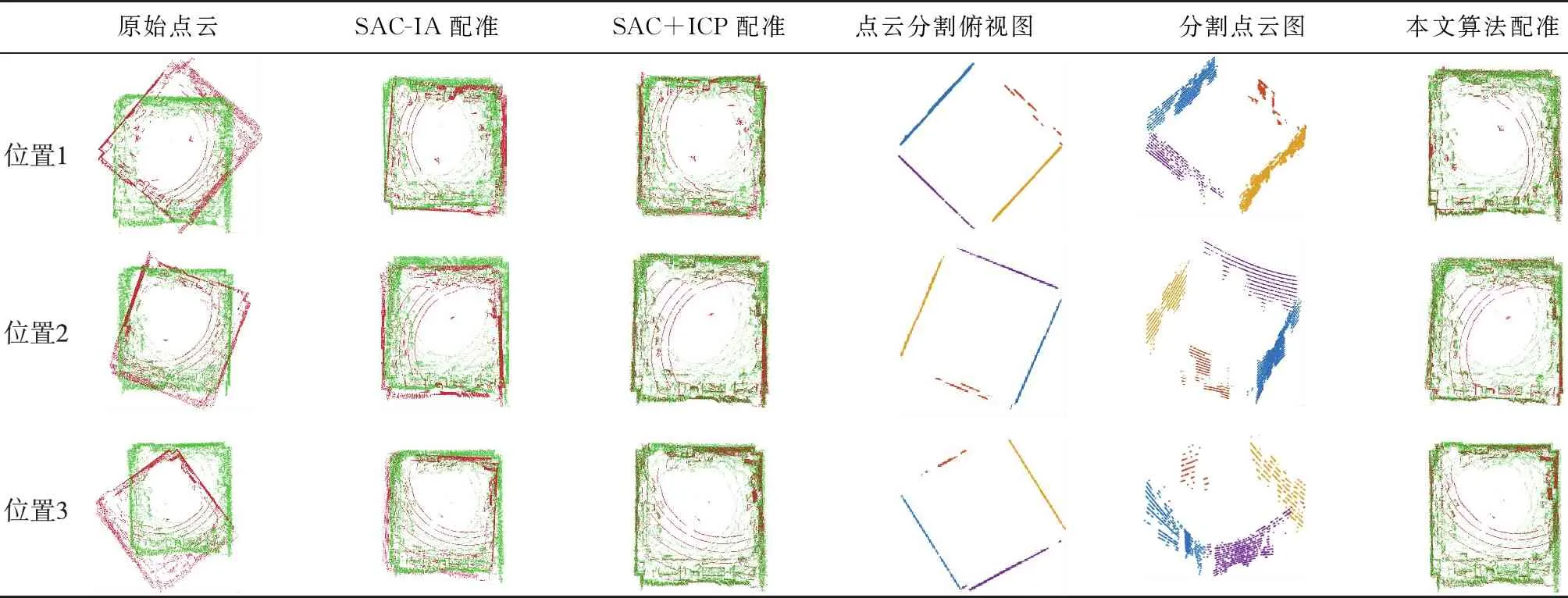
表5 点云配准对比
由表5可见,经本文分割算法处理后得到的平面点质量较高,其具体的点云配准精度对比分析如表6所示。
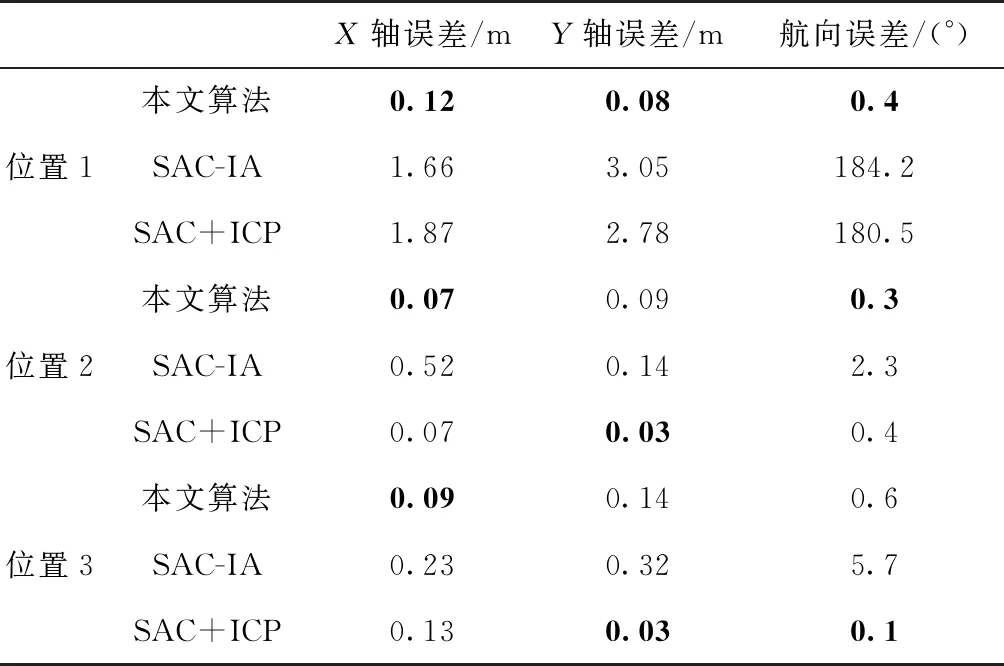
表6 点云配准精度对比
由表6可得,在实际环境中,本文算法与SAC+ICP组合算法精度相当。然而,传统算法在位置1处陷入了局部最优解,产生了错误的导航解算方向,在该情况下本文算法仍保持了较高的解算精度。
(3)计算效率对比分析
本文算法与传统算法计算时间统计如表7所示。

表7 计算效率对比Tab.7 Computational efficiency comparison
由表7可得,本文算法的平均用时为1.8s,SAC-IA算法的平均用时为7.0s,SAC +ICP算法的平均用时为8.9s。因此,在实地实验中,本文算法的计算效率约是SAC-IA算法的3.9倍,是SAC +ICP算法的5倍,与仿真环境中计算效率结果一致。
4 结论
针对传统点云位姿初始化算法计算量大、易陷入局部最优的问题,本文提出了一种面向大型结构化场景的点云位姿初始化方法。结合封闭环境空间模型的特点,对面特征提取、特征关联、位姿解算策略进行了研究。通过Gazebo仿真与室内结构化场景进行验证,可以得到如下结论:
1)本文利用结构化环境特点,采用空间模型化思想进行点云特征配准,避免了无人系统位姿初始化过程中的局部最优问题,并且具有较高的位姿解算精度;
2)不同于传统基于迭代的优化方法,本文采用线性最小二乘进行位姿求解,提高了算法的计算效率。
