基于固定阈值事件触发扩张状态观测器的多智能体协同目标环绕控制

邵星灵，岳晓辉，刘 俊，李 杰，唐 军

(1.中北大学仪器与电子学院，太原 030051; 2.中北大学仪器科学与动态测试教育部重点实验室，太原 030051)

0 引言

多智能体系统是由若干个具有有限计算、通信、控制能力的个体，借助特定的信息交互机制所形成的一类高度可重构、按需设计、分布式自主智能的网络化自治系统，因具备显著的任务执行效能、鲁棒性与灵活性，引发了包括物理、生物、军事、社会和工程科学等领域国内外研究学者的广泛关注[1-2]。分布式多智能体协同控制技术是确保多智能体系统高效、自主协作的关键使能技术[3-4]，其内涵在于通过邻居间的局部信息交互与分享，基于可利用的量测信息设计多智能体一致性协议，使得智能体相关状态趋同，从而实现既定的共同控制目标。根据具体控制任务的不同，多智能体分布式协同控制可大致分为协同一致性[5]、协同编队[6-7]、定点集结[8]和协同目标跟踪[9]等。

协同目标跟踪是多智能体系统的主要应用场景之一，最具代表性的载体形式如多无人机协同目标跟踪[10-11]和多无人车协作目标包围等，具有明显的军民两用价值。例如，在军事领域，为适应复杂动态战场环境和侦察、打击、毁伤评估等多样化作战任务需求，往往需要在指定的空域内部署多无人机系统,对敌方敏感目标执行协同环绕观测与隐蔽性跟踪任务，最终在确保自身安全性的前提下，实现对非合作目标的多维度信息收集与实时精准定位功能；在民用场合，为实现核电站核能源泄露或化工厂危险化学气体溯源追踪、监测与危险评估，以高效率、低成本、无人员伤亡为特征的多无人机系统以可变的绕飞半径,对污染源目标进行协同监测已成为应对以上难题的重要手段。不难发现，为确保复杂环境下顺利执行上述协同目标跟踪任务，通过调整多智能体自身与目标及其他智能体之间的相对位置及相位分布，以目标为圆心、最佳观测距离为半径实施协同伙伴绕飞循环跟踪，即所谓的多智能体协同目标环绕控制技术，是发挥多智能体群体目标跟踪任务效能、实现重要区域/隐蔽目标的特征深度挖掘与学习分类、增强自主与协作能力的关键。与持续目标跟踪模式相比，具有在高度隐蔽性条件下实现全方位目标动态覆盖、防止目标信息丢失或机动逃逸等优势。然而，复杂未知的运行环境、严苛的任务约束、目标运动信息的不确定性给多智能体协同目标环绕控制技术提出了诸多挑战，具体表现在：首先，机载传感设备测量精度不足和对模型机理认识不充分，将不可避免地导致系统呈现显著的非线性特性，此外，在实际工程应用中，复杂未知的作业环境引发的多源扰动会导致单体控制性能退化，严重制约了全局精准协同控制效能；其次，为保证安全观测距离和避免相邻智能体碰撞，通常需根据特定任务剖面及多智能体数量规模设计相应的环绕半径、环绕角速度及智能体间相对角间距，如何满足上述混合约束是多智能体协同目标环绕面临的又一大技术难题；最后，受实际工作环境下探测手段匮乏、非合作式目标运动特性难以预测等因素制约，目标关键信息的获取与感知往往具有极大的不确定性。特别地，对于高机动的运动目标，往往需要多智能体具有更高效、敏捷的协作能力和反应速度，以完成对目标的实时监测和跟踪。因此，亟需构建具有强抗扰性、可满足混合约束、适应目标运动不确定性的协同控制方法，是解决多智能体系统协同目标环绕问题的重要途径，也是未来复杂作战/作业环境下多样化任务驱动下多智能体一致性技术的主要发展趋势。

国内外研究学者针对单智能体环绕追踪目标的研究工作起步较早，取得了大量具有借鉴价值的学术成果。美国空军研究实验室(Air Force Rese-arch Laboratory，AFRL)的Cao等[12]提出了一种基于相对距离和相对速度的控制方案，通过设计合适的Lyapunov函数，完成了任意初始位置下对静止目标的环绕跟踪。澳大利亚国立大学的Deghat等[13]针对目标监测问题，设计了不依赖目标位置的控制器和观测器，实现了非完整机器人在纯方位量测下对目标的环绕跟踪。大连海事大学的Liu等[14]仅利用相对视线距离和相对视线角的量测信息，在参数不确定性、未建模动态和环境干扰并存的情况下，实现了欠驱动无人船对未知运动目标的追踪。韩国忠南大学的Oh等[15]提出了一种基于微分几何的对峙跟踪制导律,并通过实验验证了该方法的有效性。CEM实验室的Ghommam等[16]针对速度未知且时变的移动目标，提出了一种基于视觉的四旋翼无人机环绕目标跟踪算法，通过摄像机确定四旋翼相对于目标的位置，实现了特定高度下四旋翼以指定半径对运动目标的环绕观测。南京理工大学的Zhang等[17]研究了一种考虑目标状态的控制方案，结合饱和控制和有限时间控制技术，确保了无人机和目标之间的相对距离在有限时间内收敛到预设的期望值。

相对于单体目标跟踪，受限于多体跟踪目标任务的复杂性，针对多智能体协同目标环绕的研究相对迟缓，目前还处于起步阶段。南京理工大学的Zhang等[18]利用有限时间一致性协议，实现了多个非完整机器人对单目标的协同环绕跟踪。加拿大皇家军事学院的Marasco等[19]通过对非线性分散系统的分析, 实现了一组无人机对单一目标的包围控制。湖南大学的Yi等[20]针对协同目标环绕跟踪问题，基于相位协同的分布式控制策略，在无扰环境下完成了既定的控制目标。

然而，上述研究结果在目标量测信息的依赖性、处理复杂多扰的不确定性、满足目标环绕所需的混合约束条件等方面存在一些不足：首先，大部分控制或制导律设计都假定目标量测信息足够丰富，即目标的速度和加速度都是精确可测的，在现实中受多种因素制约往往难以满足；其次，已有研究对目标跟踪过程中广泛存在的不确定性欠缺考虑，对复杂多扰环境施加于闭环控制性能的影响缺乏重视；此外，如何在多智能体分布式一致性框架下，构造合适的相位一致性协议，满足所必须的混合约束条件目前还是开放性问题。

本文在总结国内外相关研究工作不足的基础上，提出了一种基于固定阈值事件触发扩张状态观测器(Extended State Observer based on a Fixed Thresh-old Event，FTESO)的多智能体协同目标环绕控制方法。与已报道相关工作的区别之处在于：

1) 与已有的基于领航—跟随合作式框架下的多智能体时变编队控制策略[26-27]相比，其设计目标主要关注多条参数化路径上的位置同步，领航者信息往往事先已知或者存在有效通信链路可以获得。而本文解决的是一种针对未知运动目标的非合作式协同环绕跟踪问题，环绕任务需要绕飞半径、环绕角速度和相对角间距达到预先设计要求；此外，由于待跟踪的目标与多智能体之间不存在主动通信，其量测信息不够丰富，如速度、加速度往往不可测或测不准，因此该协同任务处置更具挑战性。

2) 与已报道的基于Lyapunov导航向量场的目标环绕制导律[28-29]相比，其构造过程中大多假设目标速度与加速度可测；而本文提出的多智能体相位协同一致性协议不依赖目标速度及加速度信息，并且可确保环绕半径、环绕角速度和相对角间距达到预先设计要求，可实现无需目标速度和加速度先验信息条件下的多智能体协同目标包围控制。

3) 与文献[21]涉及的依赖连续信息传输/更新的ESO相比，设计了一种FTESO，不仅能够对相对速度和多源未知扰动进行同步精确估计，而且可以通过调节事件触发阈值，显著降低单体测量端的信息更新与传输频率，在不影响环绕跟踪品质的前提下有效节约了单体计算/能量资源。

1 预备知识与问题描述

1.1 图论

如果将每个多智能体都视为一个节点，单体间存在的信息交互看成连接节点的边，那么整个系统的通信拓扑结构可以通过无向图G={V,E,A}来刻画。其中V={1,2,…,N}表示点集，E⊆V×V表示边集，A=[aij]∈RN×N表示加权邻接矩阵。无向边(j,i)=(i,j)∈E表示节点i和它的邻居j之间可以进行信息交互，此时对应的边权重aji=aij=1；否则，aij=0。假设系统中不存在自环，即aii=0。

引理1[22-23]对于无向图G中∀i,j∈V，有

引理2[22-23]若无向图G是连通的，则

1.2 问题描述

考虑一个由N个智能体组成的同构多智能体系统，对于其中的任何一个智能体，运动学模型可以描述为

(1)

式中，pi=[pi,x,pi,y]T和vi=[vi,x,vi,y]T分别代表智能体i的位置和速度矢量；fi(pi,vi)是一个与系统状态相关的未知非线性函数;ui=[ui,x,ui,y]T表示智能体i的控制输入;Δi=[Δi,x,Δi,y]T表示施加在智能体i上的未知有界外部干扰。值得指出的是，本文所考虑的多智能体模型可以涵盖一大类非线性不确定物理系统，如无人机、无人船、机械臂等，与文献[7]涉及的线性多智能体对象相比，充分考虑了系统未知模型非线性和外部环境扰动的影响。此外，本文并不需要全状态可测，讨论了更为一般和实际的输出反馈情形。

定义运动目标的位置为pt=[pt,x,pt,y]T。如图1所示，在惯性坐标系E={Xe,Ye}下，智能体i与目标之间的相对距离和相对视线角可以表征为

(2)

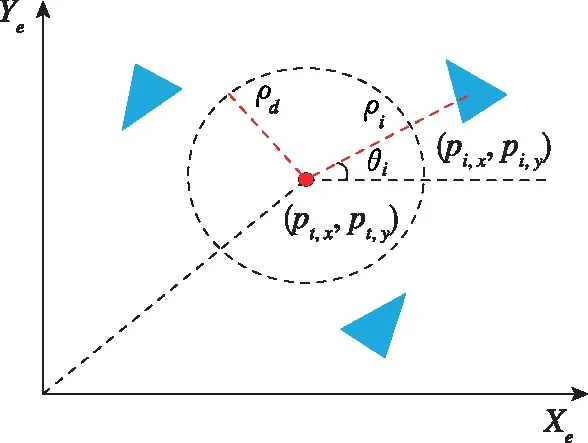
图1 多智能体协同目标对峙跟踪示意图Fig.1 Schematic diagram of multi-agent cooperative target confrontation tracking

本文的任务是达成控制目标(3)～(5)，完成多智能体对未知目标的协同环绕跟踪，确保每个智能体以期望的环绕半径和环绕角速度对目标实施对峙封锁；此外通过调控智能体间的相对角间距，实现对目标的全方位动态监测。

(3)

(4)

(5)

其中，ρd和ωd分别代表期望的环绕半径和环绕角速度；φij代表智能体间期望的环绕角间距，满足φij=-φji∈[-π,π]。

2 控制器设计

2.1 FTESO构造

根据智能体i与目标的相对运动关系，构建相对运动学模型如下

(6)

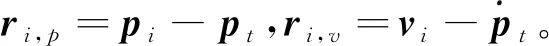
(7)

(8)

设计固定阈值事件触发条件为

(9)

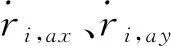
假设2[24]存在正定函数V,B∶R3→R和正常数λi1、λi2、λi3、λi4、ci1、ci2满足如下不等式

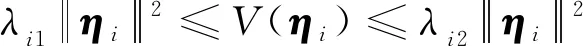
(10)

(11)

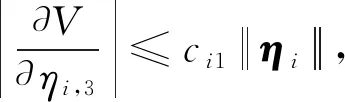
(12)

其中，ηi(t)=[ηi,1,ηi,2,ηi,3]T∈R3，i=1,2,…,N。

(13)

固定阈值事件触发条件可改写为

(14)

(15)

其中

证明：定义FTESO的观测误差为

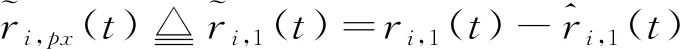
(16)

从而归一化观测误差可描述为

(17)

对ηi,m求导，并结合式(13)和式(17)可得

m=1,2

(18)

且

(19)

整理式(18)～式(19)可得

(20)

借助假设1和2，利用式(13)和式(17)，则正定Lyapunov函数V关于时间的导数可以表示为

(21)

随后，进一步可得

(22)

(23)

(24)

其中，对于式(24)右端中的第一项可放缩为

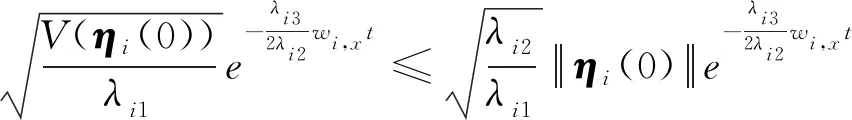
(25)

对于第二项，可放缩为如下形式

(26)

整合式(24)～式(26)，观测误差的上界可表示为

(27)

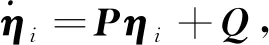
2.2 一致性协议设计

图2所示为多智能体协同目标环绕的控制结构框图。基于分布式一致性原理，构造具有饱和特性的多智能体相位同步误差为

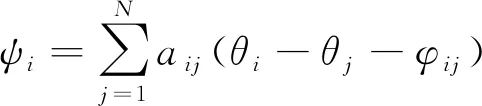
(28)

式中，ξ是正常数。当智能体i与智能体j之间存在信息交互时，aij=1；否则，aij=0。

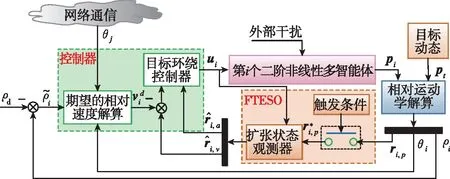
图2 多智能体协同目标环绕的控制结构框图Fig.2 Control structure diagram of multi-agent system circle around the target

根据速度方向场理论可知，任意方向的速度向量均可由空间任意两点连线的径向量和垂直于该连线的法向量构成。如图3所示，本文假定智能体都逆时针方向环绕目标，则以目标为坐标原点建立视目坐标系，目标与智能体i之间的期望相对速度可设计为

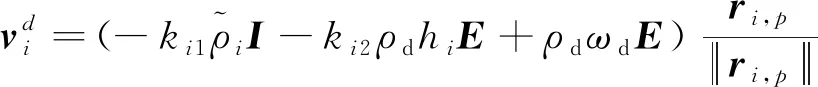
(29)

图3 期望的相对速度示意图Fig.3 Schematic of the desired relative velocity

(30)

对式(30)求导，并结合式(8)可得

(31)

基于式(31)和FTESO的估计结果，设计不依赖目标加速度信息的多智能体相位一致性控制协议

(32)

2.3 稳定性分析

联立式(9)和式(31)、式(32)，以ri,p和ei,v为变量的相对运动系统动态可重写为

(33)

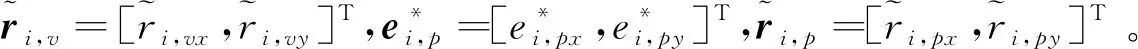
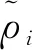
μi1=ki1-1>0,μi2=ki3-1>0,i=1,2…，N

(34)

证构造Lyapunov函数为

(35)

对V1求导并考虑式(33)，可得

(36)

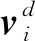
(37)

利用Young’s不等式，结合固定阈值事件触发条件(9)和定理1，可得

(38)

其中，κi=[κi,x,κi,y]T,δi=[δi,x,δi,y]T。

(39)

(40)

求解式(40)可得

(41)

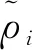
(42)

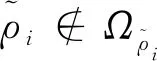
注意到式(2)中的视线角θi，其导数可表示为

=ωd-ki2hi+γi

(43)

其中

(44)

(45)

(46)

构造Lyapunov函数为

(47)

对V2求导，并应用引理1可得

γi-γj)]

(48)

对式(48)在(0,t)上积分并移项得

(49)

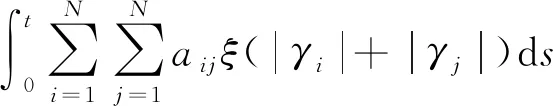
(50)

需要说明的是，本文考虑的分布式控制策略可适用于任意数量的多智能体协同目标环绕跟踪任务。由于每个智能体仅与其相邻的智能体进行信息交互，故相较于集中式控制策略，分布式控制策略具有更强的灵活性、扩展性以及容错性，可按需设计增加或减少智能体个数。此外，本文涉及的分布式控制策略可以充分节省每个智能体的计算性能，有效降低控制系统对传感器和通信带宽的要求，同时所提单体控制算法的具体实现都是基于代数和递推方程组，并不存在数值优化和迭代等耗时程序，因此目前主流的数字微处理器完全可以胜任该算法的实时执行与处理。

3 仿真验证

本文以6个智能体为例，构建多智能体网络系统，分别对不同运动模式的目标实施协同环绕跟踪，以验证所提控制算法的有效性。智能体间的通信拓扑结构如图4所示，表1具体给出了智能体与目标的初始位置参数、控制目标参数及一致性协议增益。此外，每个智能体的模型未知非线性为

f1=[0.1(p1,x+p1,y)sin(0.2t), 0.1(v1,x+v1,y)sin(0.2t)]T

f2=[0.1(p2,x+p2,y)cos(0.8t), 0.1(v2,x+v2,y)cos(0.8t)]T

f3=[0.1(p3,x+p3,y)sin(0.5t), 0.1(v3,x+v3,y)sin(0.5t)]T

图4 智能体间的通信拓扑Fig.4 Communication topology among agents

表1 仿真初始化参数

f4=[0.1(p3,x+p3,y)sin(0.2t), 0.1(v3,x+v3,y)cos(0.2t)]T

f5=[0.1(p3,x+p3,y)sin(0.8t), 0.1(v3,x+v3,y)cos(0.8t)]T

f6=[0.1(p3,x+p3,y)sin(0.5t), 0.1(v3,x+v3,y)cos(0.5t)]T

作用于每个智能体的外部干扰为

Δ1=[0.5(sin(0.5t)-cos(0.8t))， 0.5(cos(0.5t)-cos(0.8t))]T

Δ2=[0.5(sint+sin(0.5t))， 0.5(cost+sin(0.5t))]T

Δ3=[0.5(sint-cos(0.8t))， 0.5(cost-cos(0.8t))]T

Δ4=[0.5(cos(0.5t)-sin(0.8t))， 0.5(sin(0.5t)-sin(0.8t))]T

Δ5=[0.5(cost+cos(0.5t))， 0.5(sint+cos(0.5t))]T

Δ6=[0.5(cost-sin(0.8t))， 0.5(sint-sin(0.8t))]T

(1)工况1：目标作匀速直线运动

图5 工况1的协同环绕控制效果Fig.5 Synergistic encirclement control effect under condition 1

图6 工况1的控制目标实现情况Fig.6 Simulation results of control objects under condition 1

图7 工况1场景下FTESO对智能体1的相对速度和集总干扰估计效果Fig.7 Estimation effect of relative velocity and the lumped disturbance utilizing FTESO under condition 1

(2)工况2：目标作余弦机动

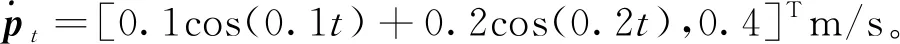
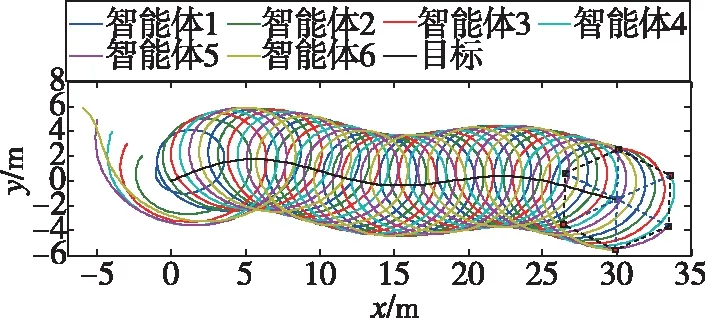
图8 工况2的协同环绕控制效果Fig.8 Synergistic encirclement control effect under condition 2

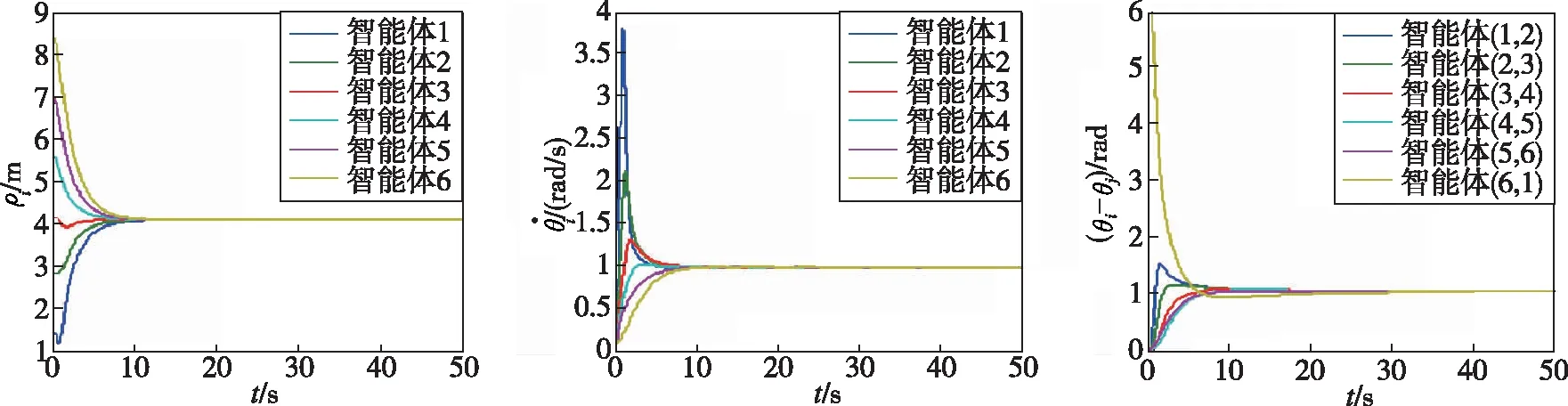
图9 工况2的控制目标实现效果Fig.9 Simulation results of control objects under condition2

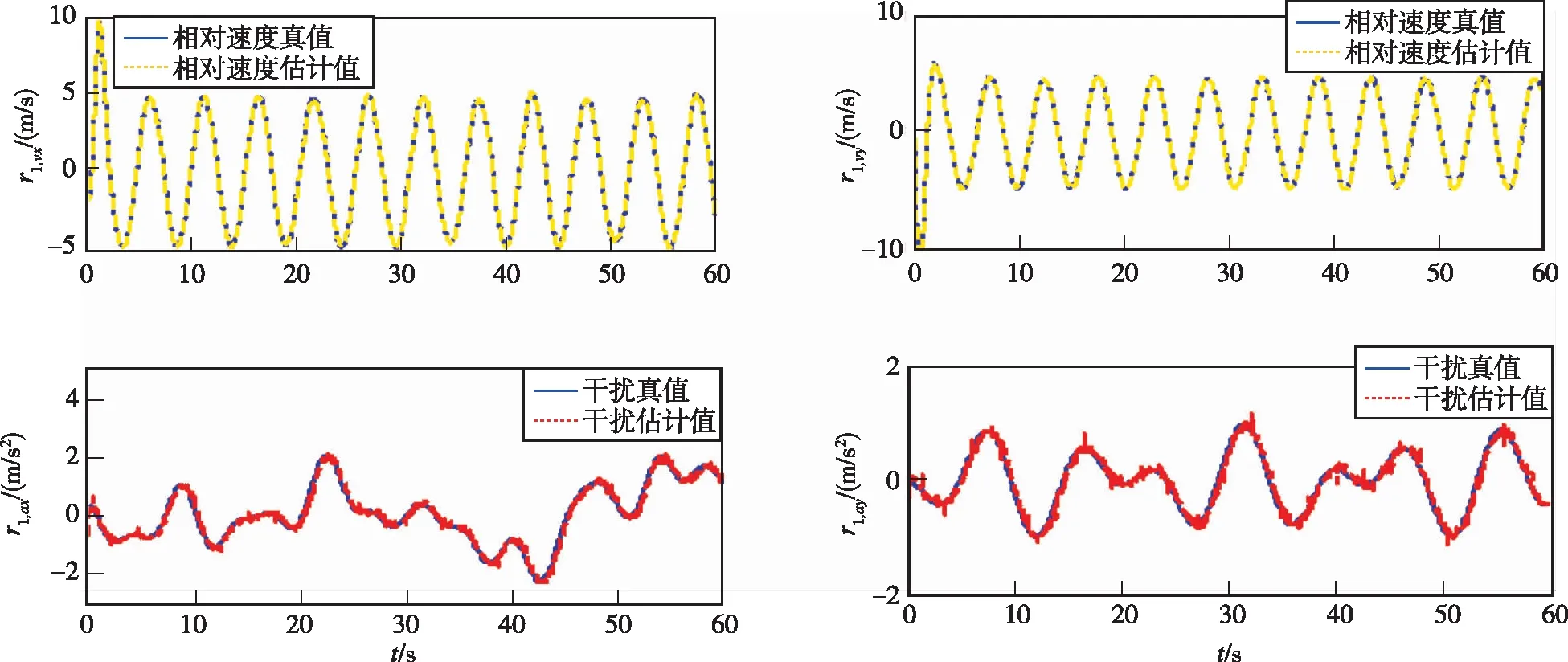
图10 工况2场景下FTESO对智能体1的相对速度和集总干扰估计效果Fig.10 Estimation effect of relative velocity and the lumped disturbance utilizing FTESO under condition 2

(3)FTESO和ESO的性能对比

以智能体1为例，将FTESO与基于时间触发机制的传统ESO进行对比，以验证本文所提的FTESO在降低采样消耗方面的性能优势。为保证对比实验的公平性，所有涉及的参数与工况2保持一致，且仿真实验均在采样频率为1kHz的MATLAB/Simulink环境中进行。

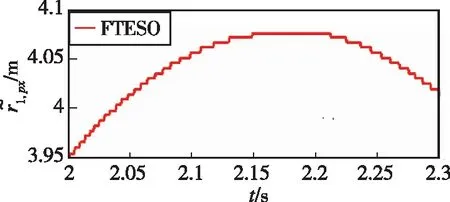
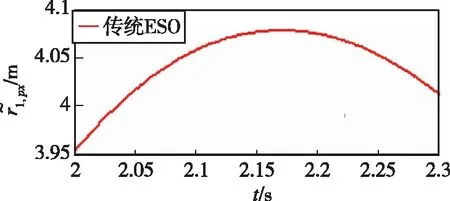
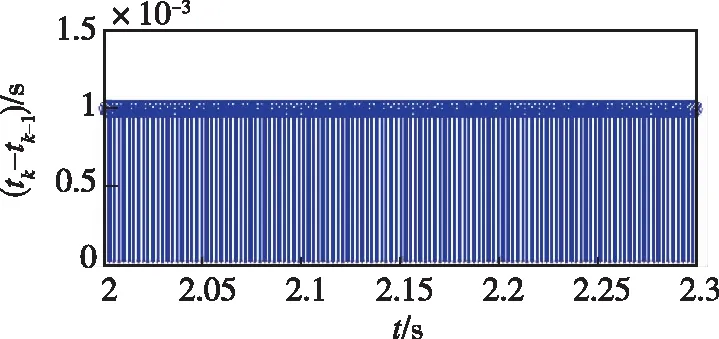
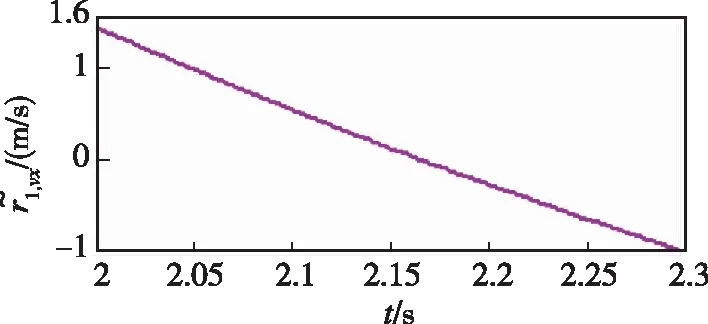
图11中(a)-(b)、(c)-(d)和(e)-(f)分别描述了传统ESO和事件触发ESO在相同条件下的观测性能对比。如图11(a)-(b)所示，FTESO能够显著降低测量端ESO的更新数据量；如图11(c)-(d)所示，相较于基于时间触发机制驱动的传统ESO，FTESO在增大采样间隔方面展现出巨大优势，可实现在非周期采样条件下对不可测相对速度和未知集总干扰的精准估计，极大地减少了触发信号的更新频次；由图11(e)-(f)可以看出，FTESO的估计效果并没有明显恶化。为进一步说明FTESO的优越性，通过对两种不同采样机制中触发次数和估计误差进行量化比较(见表2)，不难发现，所提的FTESO可以在不显著牺牲观测性能的前提下，有效释放测量端信号采样与传输负担，缓解单体计算/能量资源受限的窘境。

(a)

(b)

(c)

(d)

(e)

(f)图11 FTESO和传统ESO[25]的性能比较Fig.11 Performance comparisons between FTESO and traditional ESO[25]

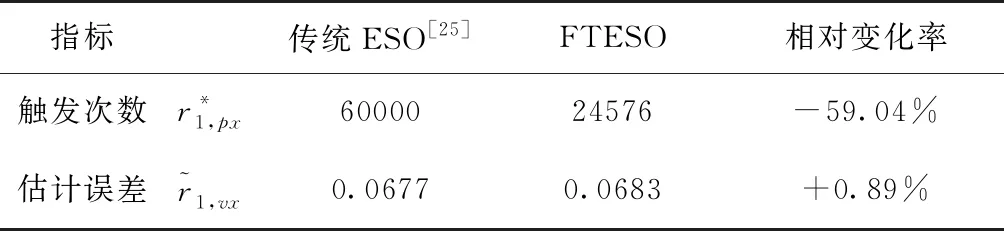
表2 FTESO和ESO观测性能对比

4 结论

本文针对外部干扰、模型非线性、目标加速度信息未知情况下多智能体的对峙目标跟踪问题，提出了一种基于固定阈值事件触发扩张状态观测器的多智能体协同目标环绕控制方案。理论证明和仿真结果表明：1)所提的FTESO可快速准确地估计出目标与各个智能体之间的相对速度和集总干扰，可确保在不牺牲估计精度的前提下，有效降低测量回路信息数据量；2)无论面对匀速直线运动目标还是余弦机动目标，本文所提一致性协议均能实现预期的协同环绕目标跟踪。值得注意的是，若进一步增大所提FTESO的触发固定阈值，势必导致测量端信号相邻采样间隔延长，干扰估计精度和目标环绕控制精度都会进一步恶化。因此，事件触发模块参数的选取应优先考虑目标环绕控制性能，在性能指标得以满足的前提下可进一步微调触发阈值，以降低多智能体测量/计算资源不必要的损耗。考虑到多智能体之间协同避障是实现协作任务安全性的前提保障，未来将会在所提策略的框架下引入势场函数法，消除多智能体之间的冲突行为，确保多智能体在目标环绕过程中具备良好的防撞规避能力。