集群空间控制框架下的四旋翼编队飞行研究

戴邵武，赵超轮，赵国荣，刘伯彦，罗鑫辉

(海军航空大学岸防兵学院，烟台 264001)

0 引言

近年来，无人机行业发展迅速，在军用和民用领域得到了广泛应用。单架无人机由于固有的局限性，无法完成复杂的任务，人们便希望通过多无人机间的协调、合作，以产生整体大于部分之和的效果。其中，编队控制问题是多无人机系统协同合作的基础和难点，也是研究的热点。根据信息交互控制策略的不同，多无人机协同控制方式主要分为集中式控制和分布式控制[1-2]。其中，集中式控制策略要求编队中至少有1架无人机能够获取其他所有无人机的状态信息，通过集中运算得到每架无人机的控制指令并发送给其他无人机，该策略控制精度高且易于实现，但编队规模受限；分布式控制策略则仅需要获取相邻几架无人机的状态信息便可实现编队，适用于大规模编队，但全局性不强。在具体编队控制方法方面，目前主流的方法有领航跟随法[3]、虚拟结构法[4]、基于行为法、人工势场法以及基于一致性理论的方法[5]。以上编队控制方法各有优劣，适用于不同的任务需求，也常组合使用以达到期望的编队控制效果[6]。本文采用的集群空间控制方法(Cluster Space Control Method)并非主流控制方法，是由美国圣塔克拉拉大学机器人系统实验室提出的一种适用于多移动机器人编队控制的理论[7]。该方法的突出优势是编队参考点的位置可任意配置，允许编队结构全自由度变化，控制精度较高。该方法目前已成功应用于无人车[8]和飞艇[9]等多智能体编队控制中，但将该方法应用到四旋翼上的研究文献很少，国内则几乎没有关于集群空间控制的文献。

四旋翼无人机因可垂直起降、定点悬停、机动灵活等优势，近年来备受关注，应用前景广阔。由于将集群空间控制方法应用到四旋翼上的研究还不深入，可供参考的文献很少，且考虑到对于无人机编队控制问题，通常先以实现二维平面编队作为基础[10]，一般选用2～4架无人机来验证所设计控制算法的有效性[11-12]。因此，本文研究了二维平面上的四旋翼编队控制问题，并以3架无人机为例说明算法的有效性。文献[8]应用集群空间控制方法，设置平面编队的参考原点位置位于3个机器人的中心，而本文将编队参考原点位置与其中1架无人机位置重合，使编队结构更为简单，以减少运算量。

对于单机控制，基于四旋翼动力学模型，采用内外环结构和经典串级PID控制实现位姿控制；对于编队控制，采用集中控制策略，在集群空间控制框架下建立编队整体与单机的运动学关系，集群控制指令由不完全微分PD控制器产生，相较常规PD控制，其抗高频干扰能力较强。

1 集群空间控制方法

集群空间控制是一种能够指定、控制、监控多移动机器人编队的理论[7]。集群空间控制的本质是将n个机器人系统视为一个实体，或称作一个集群，并用位置量、方位量、与编队形状相关的量等来表示集群属性。在设计编队控制器前，需先定义两组状态变量，分别为集群变量和单机变量。前者是基于集群属性选择的一组适合指定、控制、监控编队状态的变量；后者是基于机器人单机属性选择的一组状态变量。然后通过运动学转换建立集群变量与单机变量的联系。

1.1 集群空间变量

考虑由n个机器人组成的系统，假设每个机器人具有m个自由度，其中平移自由度为p，旋转自由度为r，即m=p+r。则n-机器人系统中所有单机相对于惯性坐标系的位置及旋转角度可由nm个变量来完整表示。换言之，完整描述n-机器人系统的状态至少需要nm个变量。假设n个机体坐标系分别由obixbiybizbi，i=1,2,…,n表示，惯性坐标系由odxdydzd表示，编队坐标系由ocxcyczc表示。

对于六自由度n-机器人系统，机体坐标系相对惯性坐标系的状态可由(xi,yi,zi,φi,θi,ψi)表示，编队坐标系相对惯性坐标系的状态可由(xc,yc,zc,φc,θc,ψc)表示，其中x、y、z表示三维位置，φ、θ、ψ表示3个姿态角。通过上述分析可知，要完整表示六自由度n-机器人系统的编队状态，至少需要6n个变量，本文将描述编队状态的变量称为集群变量，并用ci,i=1,2,…，6n表示，集群变量与(xi,yi,zi,φi,θi,ψi)和(xc,yc,zc,φc,θc,ψc)存在一定的函数关系，即

c1=f1(xc,yc,zc,φc,θc,ψc,x1,y1,z1,φ1,

θ1,ψ1,…,xn,yn,zn,φn,θn,ψn)

c2=f2(xc,yc,zc,φc,θc,ψc,x1,y1,z1,φ1,

θ1,ψ1,…,xn,yn,zn,φn,θn,ψn)

⋮

c6n=f6n(xc,yc,zc,φc,θc,ψc,x1,y1,z1,φ1,

θ1,ψ1,…,xn,yn,zn,φn,θn,ψn)

(1)

集群变量的选取根据不同任务需求会有差异，一般包括编队位置、编队方位、单机与编队的相对方位、编队形状4个方面。编队位置用于表示编队相对惯性系的位置，在单机自由度均相同的前提下，编队位置量的数量可用p表示；编队方位用于表示编队坐标系相对惯性坐标系的方位关系，编队方位量的数量可用o表示，当n≥p=3时，则o=3，否则，o=p-1；单机与编队的相对方位量表示每个单机相对编队系的方位，用nr个变量便可构成；编队形状用于描述编队的几何关系，编队形状量的数量用s表示，假设共有nm个集群变量来描述编队的状态，则s=nm-p-o-nr=(n-1)p-o。一般从以上4个方面选取集群变量，便能够清晰、直观、全面地刻画编队的状态。

1.2 集群运动学关系

因为编队控制的指令最终要发送给每个单机去执行，所以需要建立集群变量与单机变量的运动学关系。

(1)位置运动学

定义集群变量构成的向量为C，所有单机变量构成的向量为R，并分别称为集群位置向量和单机位置向量。两者均为nm维列向量，两者关系如下

(2)

(3)

称式(2)为正向位置运动学关系式，式(3)为逆向位置运动学关系式，以此建立集群变量与单机变量的联系。

(2)速度运动学

(4)

其中

(5)

式(4)实现了从单机速度向量到集群速度向量的映射。反过来，有

(6)

其中，J-1(C)为逆雅克比矩阵，为

中粮宁夏年产2万t葡萄酒及配套种植基地项目的建设内容，符合我国酿酒行业 “粮食酒向水果酒转变”的产业政策要求，是国家发展和改革委员 《产业结构调整指导目录（2011年本）》中鼓励的农产品基地建设和生态系统恢复与重建工程，同时也符合宁夏发展葡萄产业、建设优质酿酒葡萄种植基地的战略部署。

(7)

可见，随着单机数量和自由度的增加，集群变量会相应增加，运动学关系式会变得相对复杂，必然导致机间交互的信息量增大。故文献[7]中提到，在现有技术程度上，若采用集中控制策略，在该控制方法下编队机器人的数量规模大约在10个以内。

2 四旋翼编队控制系统设计

首先建立四旋翼单机模型,然后进行编队控制器设计。

2.1 四旋翼模型

本文采用十字形四旋翼，如图1所示。四旋翼是一个非线性、多变量、高度耦合、欠驱动系统[13]。假设四旋翼是刚体结构，机体几何对称、质量对称，且几何中心与重心重合。

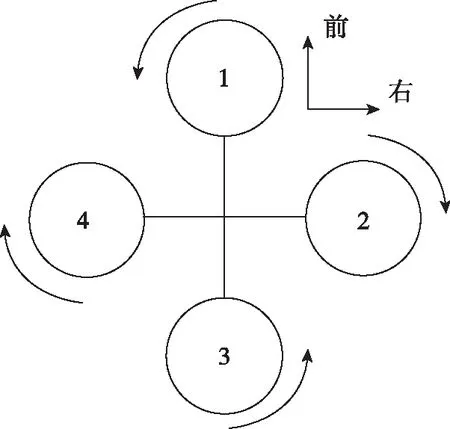
图1 十字形四旋翼Fig.1 Cross-shaped quadrotor

首先建立两个右手坐标系，即惯性北-东-地坐标系及机体坐标系，如图2所示。其中，惯性坐标系odxdydzd以地面任意一点为坐标原点，odxd轴指向北，odzd轴垂直地面向下；机体坐标系obxbybzb与四旋翼机体固连，以机体重心位置为坐标原点，obxb轴指向机头方向，obzb轴在机体对称平面内，垂直于obxb轴向下。

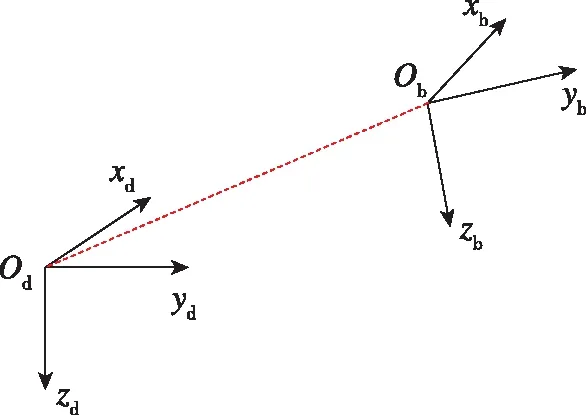
图2 惯性坐标系与机体坐标系Fig.2 Inertial and body coordinate system

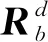
(8)

其中，cθ、sθ分别表示cosθ、sinθ，此规则同样适用于ψ、φ。

假设四旋翼在飞行过程中，俯仰角和滚转角都很小，总拉力约等于四旋翼的重力，则有下列近似：sinφ≈φ,cosφ≈1,sinθ≈θ,cosθ≈1,f≈m0g。在忽略陀螺效应、-ω×(J·ω)项及空气阻力的情况下，采用牛顿-欧拉法可以得到水平通道与高度通道相互解耦的四旋翼动力学模型[14]为

(9)

四旋翼飞行器控制采用内外环结构，内环控制姿态，外环控制位置，内外环均使用经典串级PID控制[14]。

2.2 编队控制器

本文以3架四旋翼无人机为例，设计了相应的集群控制算法，实现了二维平面内的编队控制。图3所示为相关的参考直角坐标系，分别为惯性坐标系odxdyd、编队坐标系ocxcyc、机体坐标系obixbiybi，i=1,2,3。后文中将机体坐标系简记为oixiyi。受领航跟随法启发，编队坐标系是以无人机1的中心位置为坐标原点，无人机2到无人机1中心位置连接线的延长线为ocxc轴，其垂线为ocyc轴；机体坐标系以无人机机体中心为坐标原点，机头方向为oixi轴，其垂线为oiyi轴。3架无人机的几何关系如图4所示。

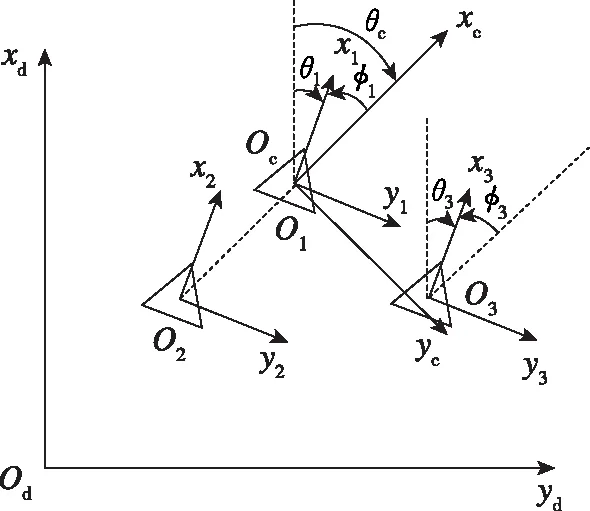
图3 平面3架无人机的参考坐标系Fig.3 Reference frames for three UAVs on the plan

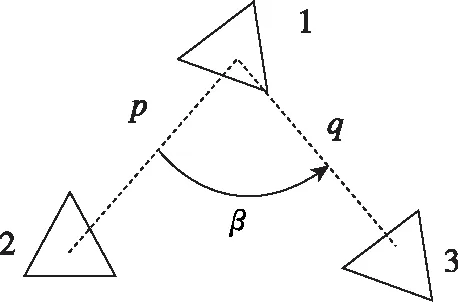
图4 3架无人机的几何关系Fig.4 Geometric relation of three UAVs

基于上述坐标系，为描述编队及单机属性，按照1.1节所述规则，首先选择一组集群变量C和一组单机变量R

C=(xc,yc,θc,φ1,φ2,φ3,p,q,β)T

(10)

R=(x1,y1,θ1,x2,y2,θ2,x3,y3,θ3)T

(11)

其中，(xc,yc)为编队参考点在惯性系下的二维位置，由于编队参考点与无人机1重合，无人机1相当于编队的领航者。(xi,yi)为无人机i在惯性系下的二维位置坐标，定义无人机i相对惯性系的偏航角θi为odxd轴到oixi轴的夹角；定义编队基准角θc为odxd轴到ocxc轴的夹角；无人机i相对编队坐标系的偏航角φi为ocxc轴到oixi轴的夹角;无人机1到2的距离为p，无人机1到3的距离为q;以无人机1为三角形顶点的角为β。

3架无人机的通信拓扑图如图5所示。无人机2和3将自身状态信息发送给无人机1，无人机1对获取的所有无人机的信息进行集中处理,解算得到各无人机的控制指令后，再发送给其他无人机。

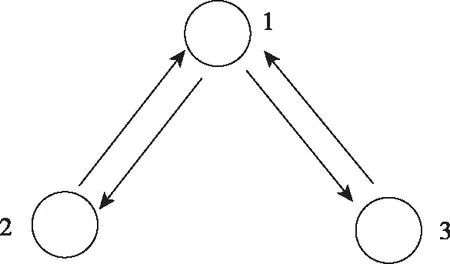
图5 3架无人机的通信拓扑图Fig.5 Communication topology of three UAVs

基于上述选择的集群和单机状态变量，下面给出了编队系统的正向及逆向位置运动学关系式。正向位置运动学方程为C=KIN(R)，展开为式(12)

(12)

逆向位置运动学方程为R=INKIN(C)，展开为式(13)

(13)

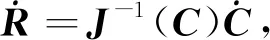
(14)

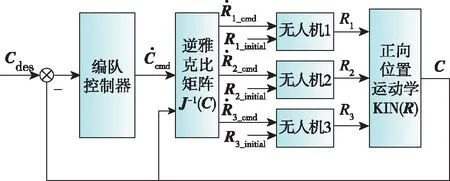
图6 编队控制框图Fig.6 Formation control architecture

出于简化的目的，同时考虑四旋翼特点，可设定在飞行过程中，无人机单机期望偏航角始终为恒定值，由单机控制器直接实现自身偏航角控制。因此，集群变量由9个简化为6个，即C=(xc,yc,θc,p,q,β)T。相应的单机变量简化为R=(x1,y1,x2,y2,x3,y3)T。

考虑到无人机在飞行过程中存在随机扰动，而常规PD控制中的微分项易引进高频干扰，使控制指令出现突跳，对控制系统不利。若在控制器中加入低通滤波器，则可明显抑制高频干扰。因此，编队控制器采用不完全微分PD控制器[15]，控制器结构如图7所示。

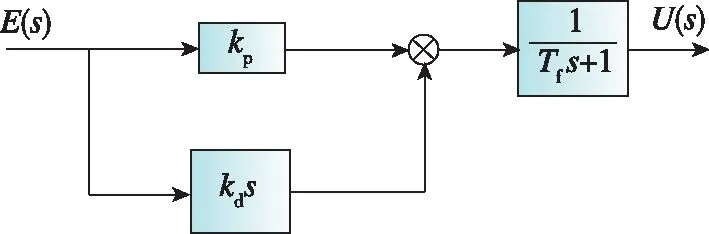
图7 不完全微分PD控制器Fig.7 Incomplete differential PD controller

最终，集群变量误差值通过编队控制器和运动学转换得到单机控制指令，进而发送给单机控制器，作为单机x、y通道的速度指令。

3 仿真分析

利用MATLAB对3架四旋翼无人机的编队控制算法进行仿真，验证其编队控制的性能。编队控制器参数如表1所示。

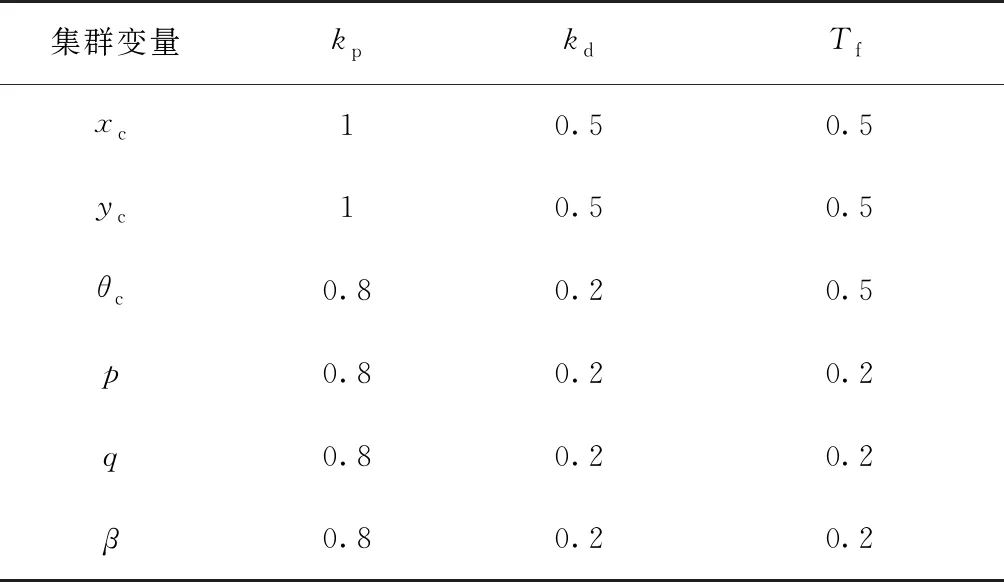
表1 不完全微分PD控制器参数

假设3架无人机均在5m高度悬停，无人机1、2、3的初始二维位置分别为(5,5)、(3,3)、(3,7)，期望的编队状态为

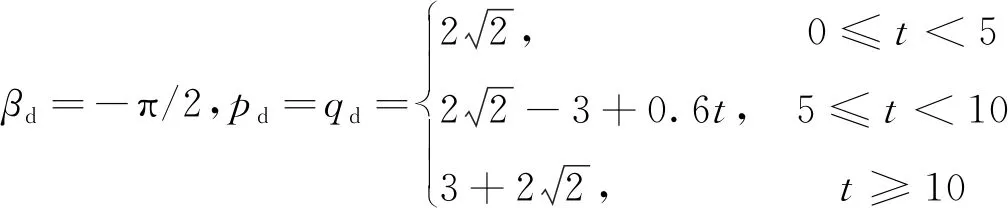
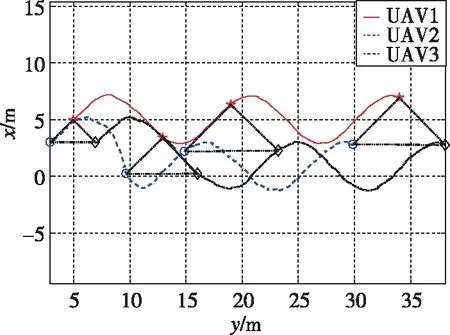
在3架无人机的实际位置输出端分别加入幅值为0.05、0.1、0.1，采样时间均为0.5s的随机干扰，仿真时间30s，仿真步长0.02s。图8(a)为编队飞行的二维轨迹，其中在0s、9s、15s、30s时刻对无人机的位置做了标记，无人机1、2、3分别用五角星、圆形和菱形表示。可见在飞行过程中，3架无人机能够形成稳定的三角形编队，且相对位置唯一确定，能够较好地实现队形放大和队形保持任务。

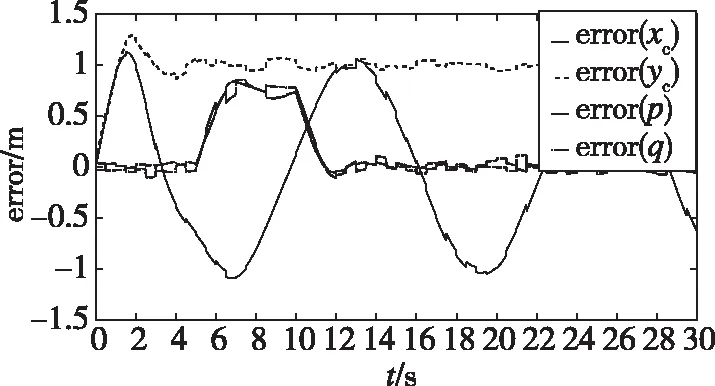
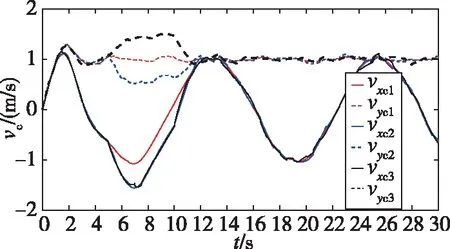
由图8(b)可见，领航者无人机1的y方向跟踪误差控制在1.3m以内，x方向跟踪误差在1.1m以内，此位置误差实质与单机控制器有关；在队形放大过程中，距离量p、q的误差在0.9m以内；在队形保持过程中，距离量p、q的误差小于0.12m，队形保持效果较好。图8(c)中，角度θc的误差小于0.015rad，β的误差小于0.04rad。图8(d)中，vxc和vyc表示发送给无人机的速度指令，数字1、2、3对应无人机编号，在5s时进行队形放大，可见速度指令进行了合理调整，在有随机信号的干扰下，指令曲线较为平滑。

图9所示为在常规PD编队控制下生成的速度指令曲线，与图8(d)对比易见，引入不完全微分能够明显抑制随机扰动对系统带来的影响。

(a)编队飞行轨迹

(b)位置、距离误差曲线

(c) 角度误差曲线

(d)3架无人机的速度指令图8 不完全微分PD编队控制仿真图Fig.8 Incomplete differential PD formation control simulation diagram

图9 常规PD编队控制下的速度指令Fig.9 Velocity commands of conventional PD formation control

4 结束语

本文主要介绍了集群空间控制方法的概念，然后将该方法应用到四旋翼编队控制中，并以3架四旋翼为例，验证了所设计编队控制算法的有效性。在考虑存在随机扰动的情况下，设计了不完全微分PD控制器以产生集群控制指令，实现了编队放大与队形保持任务。结果表明，该控制算法能够实现多架四旋翼无人机的编队控制，清晰完整地描述指定编队状态，队形保持的精度较高，与常规PD控制相比，具有较强的抗高频干扰能力。