基于FFT 的数字回波信号时域波形优化研究*

梁书娟

（郑州理工职业学院信息工程系，河南 新郑 451150）

0 引言

信号经过不定参数系统后，得到确定输出以满足预设的系统要求［1］。在实际环境中，往往需要利用不同的输入信号调整系统输出［2］。为实现不同的信号输出在信息系统本身参数未知的条件下达到预期的性能或完成特定的任务，对于系统的输出要求可以由不同的输入信号优化进行控制。

波形优化指的是电子信息系统采用不同的准则函数，根据信号环境信息的变化，自适应优化发射波形，以实现提高某种特定任务下性能的过程［3］。当信号环境信息变化时，依据某种优化准则函数，将得到变化的最优发射波形。通常情况下，信号环境中的信号处理系统本身参数未知，仅已知系统输出信号数据以及环境信息，需要对输入信号进行控制与分类，类似盲信号分选问题。本文通过构建数字信号波形优化模型，以确定数字信号环境截获的信号数据的种类数量，即为系统的数量；同时，构建的模型能够对信号数据的归属作出判断。

1 问题分析

式（5）中，R 表示截获信道中噪声信号的自相关矩阵，同时R 也是Hermitian-Toeplitz 矩阵，可表示为：

对模板进行归一化处理［6］。因此，使用快速傅里叶变换方法对环境信号及其对应的最优波形信号进行变换得出其特征值，再根据模型中的数据分类得出波形优化准则的数量［7］。因此，需要构建基于快速傅里叶变换的模型来确定波形优化准则的个数。根据截获信号数据的大小，合理确定优化准则的分类要求，得到波形优化准则的分类；再将每条数据分类到各准则中，并以此来分析该数据之间的关联性。

2 模型的建立与分析

1）N/2 点DFT［12］

按照n 的奇偶性把x（n）分解为两个点N/2 的子序列，然后分别为两组做DFT，可以表示为：

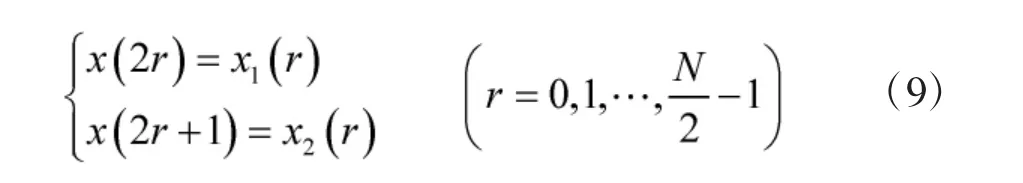
则可将DFT 化为：

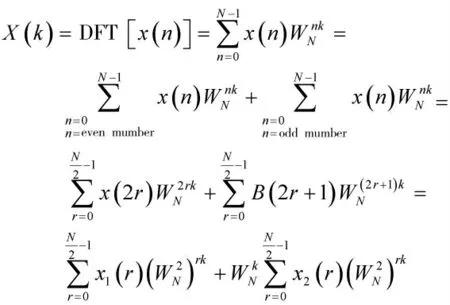
3 模型求解

基于上述理论原理，本文运用matlab 编程实现该变换。首先，使用matlab 读取截获的不同信号中的数据，并绘制时域波形的图像，按照环境信号和最优波形信号绘制同一幅图的思想进行绘制。部分波形图见图1～图4。

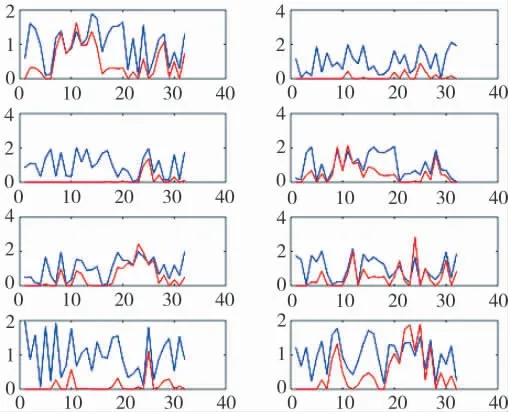
图1 信号波形示意图1

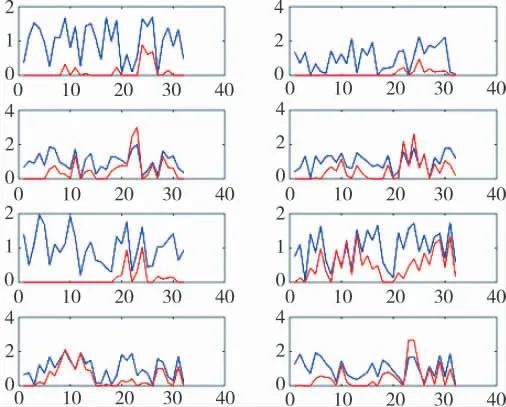
图2 信号波形示意图2

其中，蓝色表示环境信号，红色表示最优波形信号。从图可以看出，环境信号经过优化准则后被抑制掉了一部分，同时，未被抑制的也被等幅缩小或者放大。信号数据进行快速傅里叶变换，由上述波形得到如下结果。

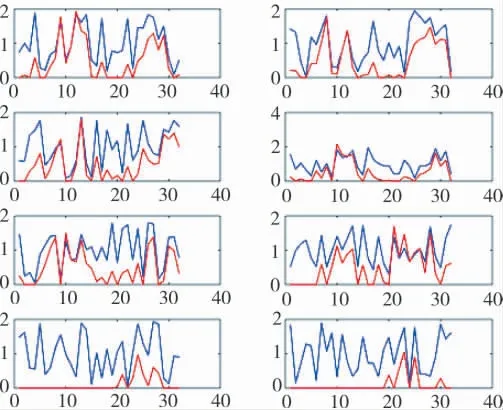
图3 信号波形示意图3

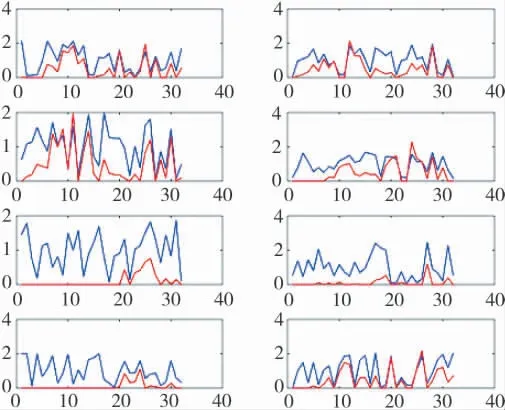
图4 信号波形示意图4

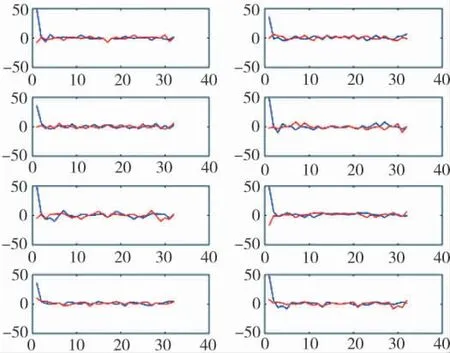
图5 经FFT 后结果1

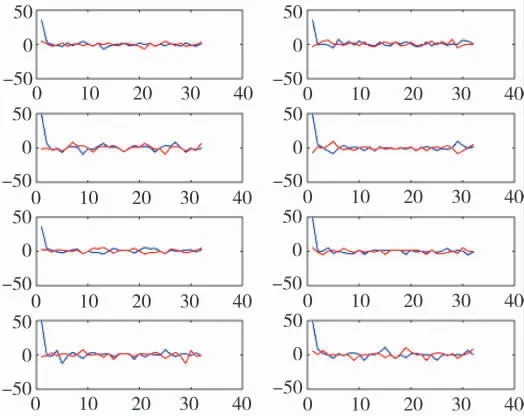
图6 经FFT 后结果2

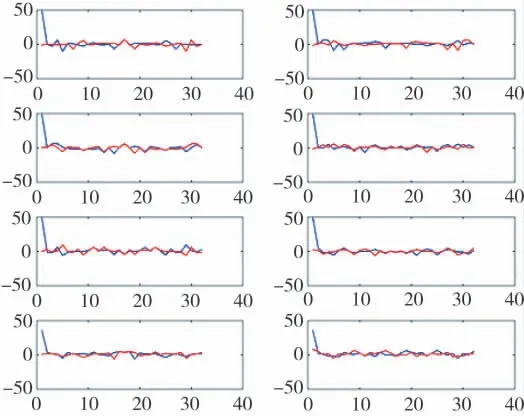
图7 经FFT 后结果3

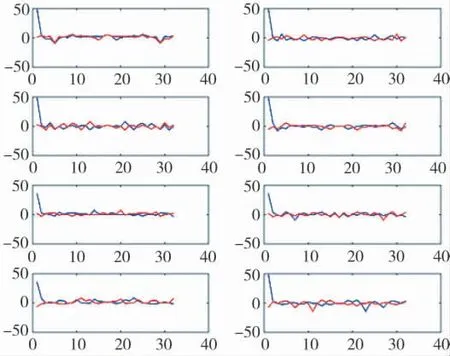
图8 经FFT 后结果4

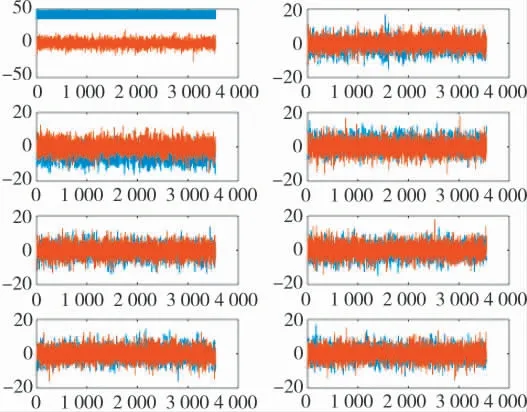
图9 FFT 后信号波形

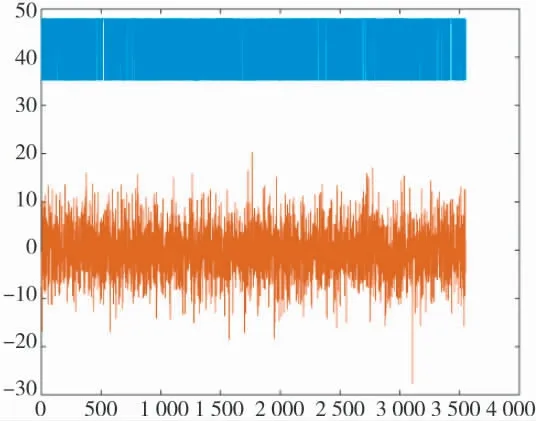
图10 信号特征图

从上图可以发现，数据经过FFT 后，在第一个位置之外的值都被完全抑制，最终得到信号的特征值。因此，可以此作为识别优化准则的要点。图9 为信号在FFT 后，随机选取了8 组采集信号的波形示意图，从图中不难看出，第1 幅图有较为明显的区分度，除此之外，其他的图都杂乱无章，且相近。因此，本文以第1 幅图为划分波形优化准则的依据，其原始图如图10 所示。从图10 可以发现，环境信号在整个过程中变化不大，经过波形优化之后的最优波形信号连续且循环。因此，可以用最优波形信号的数值大小来划分波形优化准则的数量。

设定如下准则进行归类：准则1：FFT 变化后，信号特征值小于等于-10；准则2：FFT 变化后，信号特征值大于-10，小于等于-5；准则3：FFT 变化后，信号特征值大于-5，小于等于0；准则4：FFT 变化后，信号特征值大于0，小于等于5；准则5：FFT 变化后，信号特征值大于5，小于等于10；准则6：FFT变化后，信号特征值大于10。综上所述，可以得出共有6 个优化准则。

4 结论

本文利用FFT 算法对信号进行了处理，并以此来对信号波形函数进行分类，得到了较好的结果，区分出了波形优化函数的数量。通过本文的建模研究，可以用来解决实际问题中波形优化函数未知的问题。使用DFT 的改进算法FFT 对附件中的环境信号和最优波形信号进行了处理，得到了信号在频域的结果，随后对该频域结果进行解读和信号特征分析，进一步发现可以通过该特征对信号进行分类，从而得出波形优化准则的数量。根据模型分析结果，发现共有6 个波形优化准则对环境信号进行了处理。结合信号FFT 的处理结果，通过绘图发现最优波形信号的频率是连续的，根据各条信号频域的特征值，结合对应的波形优化准则，得到各信号所属的各准则。在这些数据信号中，其频率是连续变换、近周期性变化的。