作战模式及需求不确定条件下备件供应优化

王亚东，石 全，张 芳，王 强，夏 伟，3

（1.陆军工程大学石家庄校区装备指挥与管理系，石家庄 050003；2.解放军32178 部队科技创新研究中心，北京 100012；3.陆军步兵学院石家庄校区机械化步兵系，石家庄 050003）

0 引言

在现代战争中，战场环境复杂多变、作战模式灵活多样，在不同作战任务想定下装备的使用和损耗规律各不相同，战场抢修任务以及备件供应方案也不相同。另一方面，战时的备件损耗为退化和战损共同作用下的竞争失效，且备件需求随任务开展呈波动状态。因此，如何应对战时备件供应保障中的各种不确定因素，制定一套能够应对各种情况下的备件供应方案具有重大的意义。

在战时备件供应优化方面，任骥等人假设战损件以及军需备件服从已知概率分布，利用随机优化研究了备件需求和战损件修复不确定性条件下的备件供应优化问题［1］；刘喜春研究了不确定需求下航材供应问题，采用机会约束规划，建立了不可修复备件的随机规划模型［2］；王睿等人通过求出供应渠道备件数量期望和方差，根据VARI-METEIC 方法近似估计供应渠道备件数量的概率分布，进而计算得到备件期望短缺和短缺函数方差［3］。可以看出，目前很少有文献同时从作战任务类型和需求的不确定方面研究战时备件保障优化，且通常假设备件需求为服从已知概率分布的随机变量，这与战时特殊情况备件消耗规律不尽相符。在处理供应链的不确定性时，常采用的方法有随机优化、模糊优化和鲁棒优化。随机优化中，通常需要提前知道或者假设不确定参数的分布规律，这些假设通常与实际情况不尽相符。模糊优化通常难以求解且很难保证最差情况下解的可行性。而鲁棒优化模型既不依赖不确定参数的分布，又可以保证最差情况下解的可行性。

本文旨在在战斗开始之前为整个战斗制定一套可靠的备件供应方案。首先，可由指挥员在战斗开始前拟定多种可能发生的作战想定预案。并通过备件需求预测方法，确定各战斗单位的备件需求范围。与平时备件保障不同，战时条件下一旦出现差错将对作战任务造成不可挽回的损失。因此，本文的模型应当保证所有可能发生的作战想定以及在整个需求范围内“最差情况下”的备件供应。

1 确定条件下的供应优化模型

1.1 问题描述

某次战斗开始前，为保障装备抢修任务，提前制定备件供应保障预案。要求该供应预案能够在最短的时间内以最大程度保障所有作战想定下的装备抢修任务。本文采用经典的3 级供应网络：第1级为后方仓库，根据全部作战单位的需求向野战仓库提供备件。第2 级为野战仓库，通常靠前配置完成备件的储存任务，以及向作战单位中转所需备件。第3 级为作战单位，根据装备损伤情况和抢修任务产生备件需求。

首先，设置有限个可能发生的作战想定集合s={1，2，…，S}。不同想定下，备件供应考虑的要素存在较大差异。主要包括，作战单位的备件需求数量、备件运输的延迟时间、备件库存以及运输的费用等。以上由作战想定造成的不确定性在备件供应优化模型中体现为离散不确定参数。

另一方面，即便在同一想定下，备件的需求并非固定不变或服从某一特定分布。由于备件需求预测结果存在一定误差，通常只能将备件的需求数量限定在某个区间之内，其真实值在名义值附近一定范围内波动。备件需求的不确定性在供应优化模型中体现为连续不确定参数。

战时备件供应优化模型建立在以下假设之上：1）已知所有可能发生的战斗想定；2）以某一种关键备件的供应为例。为保证抢修效率，采用换件维修方式，备件需求与换件数量一致；3）暂不考虑各级节点之间存在横向转运的情况；4）后方仓库到野战仓库、野战仓库到作战单位的备件供应延迟时间已知；5）备件在各节点之间的运输成本、备件在野战仓库中的库存成本均为已知；6）后方仓库的容量无限，且备件储备充足。野战仓库最大容量已知，且为定值。各级节点之间运力充足；7）作战单位的需求为不确定值，但其波动范围已知；不同作战单位重要程度不同，各自备件最低满足率阈值已知。

1.2 参数描述

决策变量如下：xli为第l 个后方仓库向第i 个野战仓库的备件供应量，yij为第i 个野战仓库向第j个作战单位的备件供应量。

1.3 模型构建

首先考虑确定条件下的基本模型，建立以下混合整数线性规划模型：

钢材的材质接近均质，并且力学性能与弹性塑性体接近，因此钢结构的受力情况与设计计算结构基本吻合，设计计算结果的可靠性比较高。

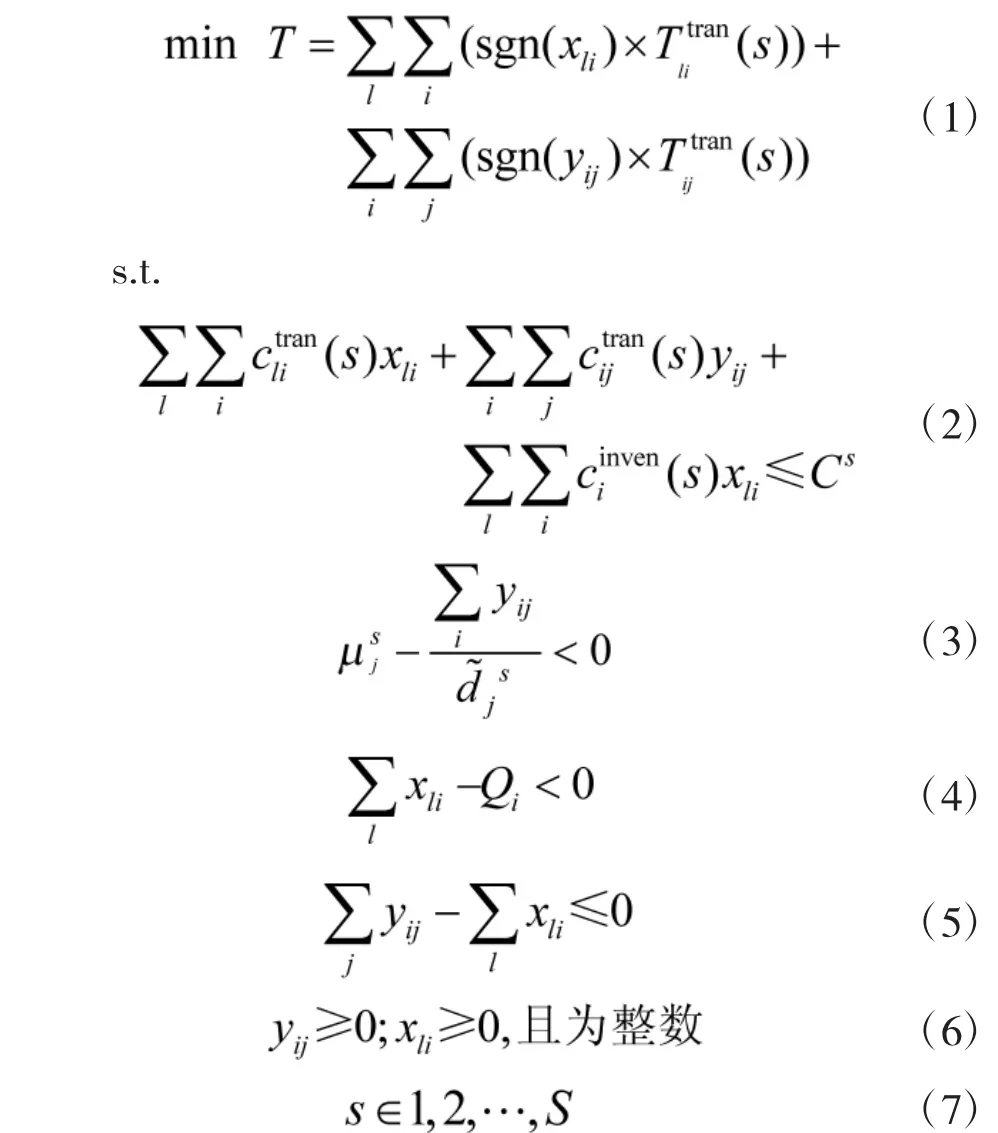
2 不确定条件下的供应优化模型

这些不确定参数，原模型是无法直接求解的。因此，需要将原模型转化为可求解的鲁棒对等形式。

2.1 作战想定不确定时的鲁棒优化模型

因此，目标函数（1）的鲁棒等价模型为：

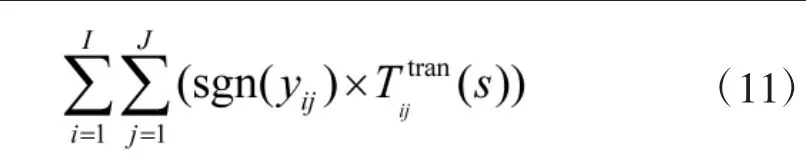
2.2 需求不确定时的鲁棒优化模型

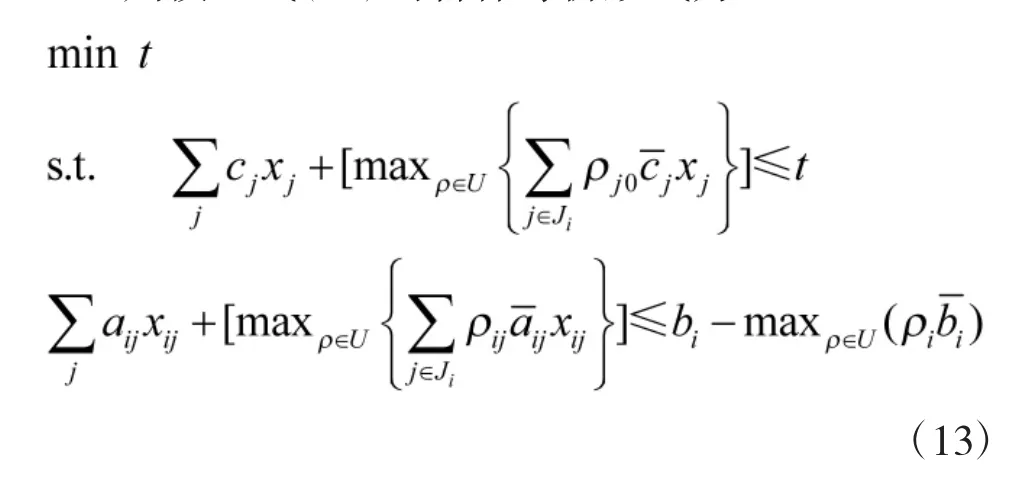
线性鲁棒优化中的不确定集合U 主要有以下几种类型：盒形（box）、多面体形（polyhedral）、椭球形（ellipsoidal）等［6］。其不确定集分别如下：

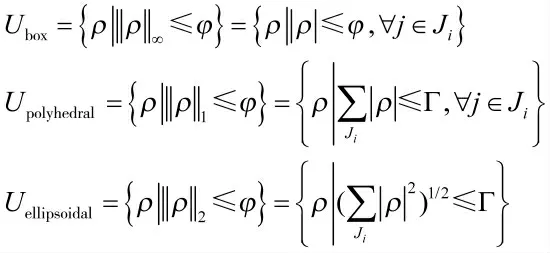
为解决“max min”优化问题，根据强对偶定理可通过求式（14）的对偶问题将其转化为“min min”问题，有：

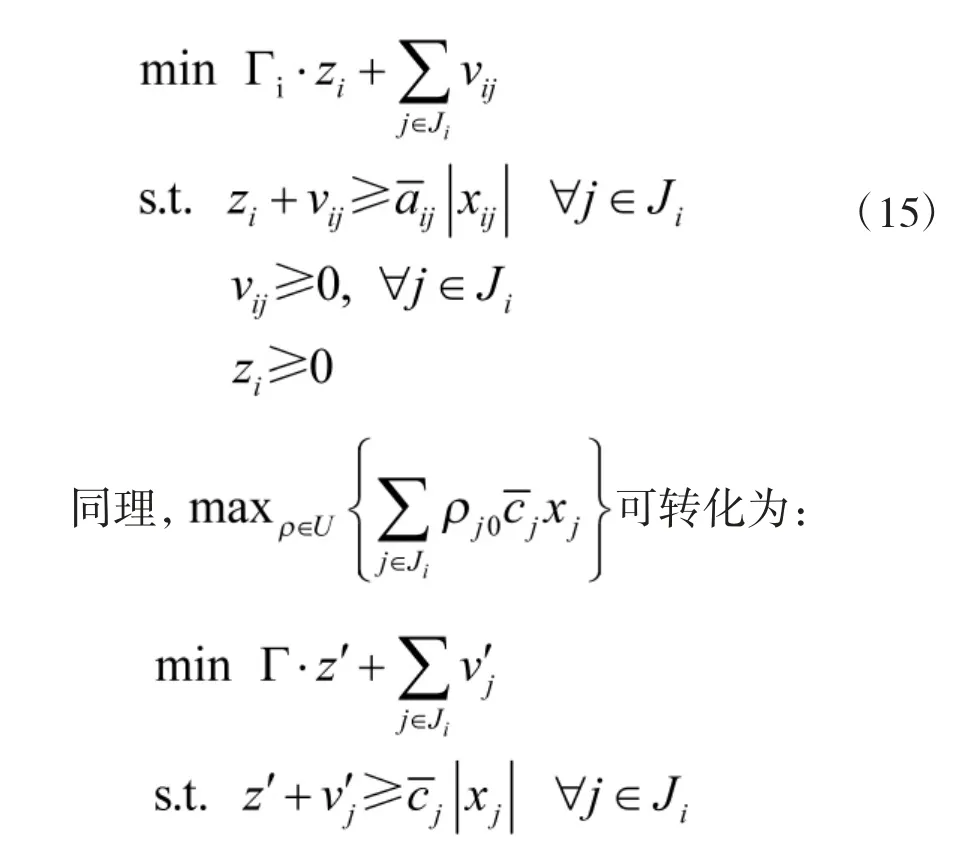
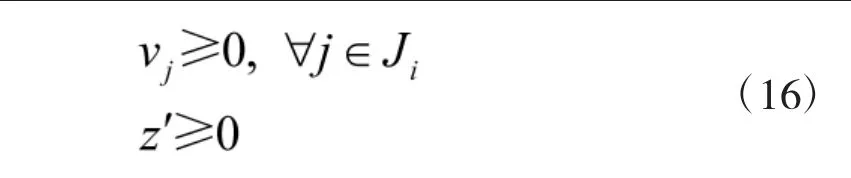
因此，模型式（13）最终的对应线性区间鲁棒优化等价模型为：

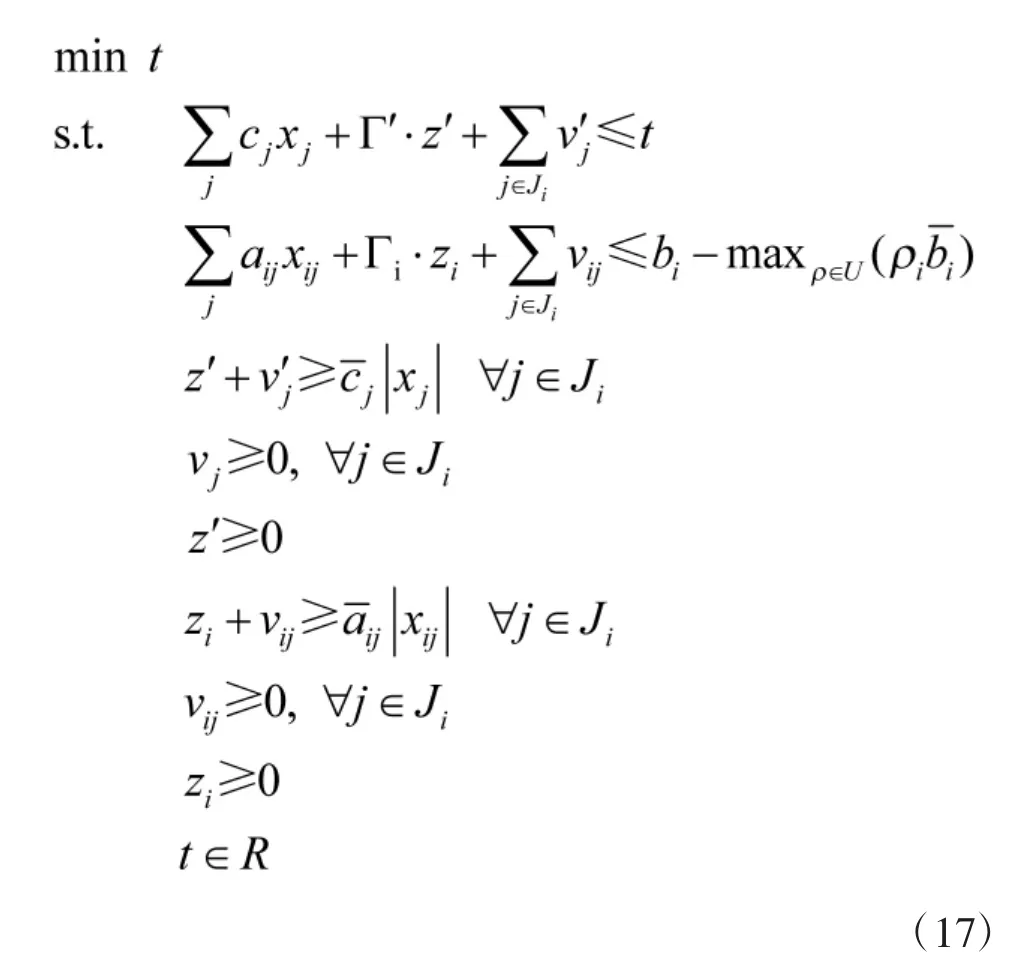
根据以上推导，目标函数式（11）的等价鲁棒模型为：

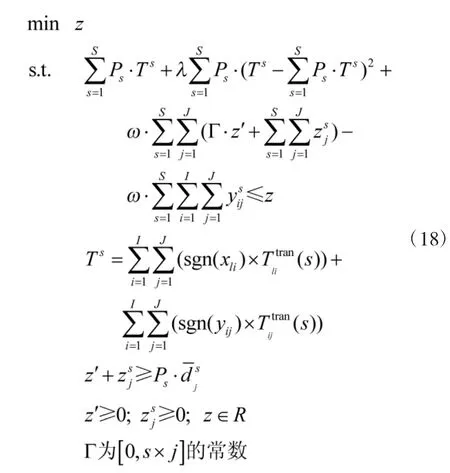
约束（3）的等价鲁棒模型为：

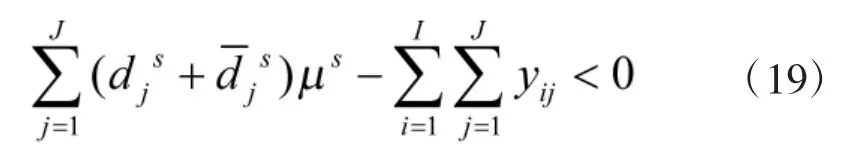
分别用式（18）和式（19）代替确定条件下模型中的目标函数式（1）和约束式（3），即为不确定条件下备件供应的鲁棒优化模型。

3 求解算法设计

差分进化算法作为一种新型智能优化算法，能够很好地解决单目标和多目标优化模型。本文选用差分进化算法对模型求解。差分进化包括4 个基本步骤：初始化、变异、交叉和选择操作。

步骤1 初始化。随机产生初始种群，种群规模为N，个体维度为D。第i 个个体上的元素xi1到xiD表示模型中决策变量的值。初始种群个体元素：

其中，randij为均匀分布［0，1］之间的随机数，CR∈［0，1］为交叉率，即当个体xi上第j 个元素xij对应的随机数小于交叉率时，该元素取变异个体对应值，否则保留原个体上的值。可以看出CR 的值越大则交叉的概率越大。

步骤5 当满足循环终止条件时，停止迭代。反之，返回步骤2。

4 算例分析

4.1 任务想定

某作战任务下的三级备件供应网络由2 个后方仓库、5 个野战仓库以及10 个作战单位组成。战斗展开前制定了5 种可能发生的战斗任务想定，需根据不同任务特点制定一套可以满足全部任务想定下的备件供应保障方案。要求供应方案能够以最短的延迟时间完成供应任务，并且保证满足作战单位备件满足率不低于规定阈值、花费成本不超过最高成本阈值。表1～下页表6 分别给出了供应网络及其节点的相关信息。

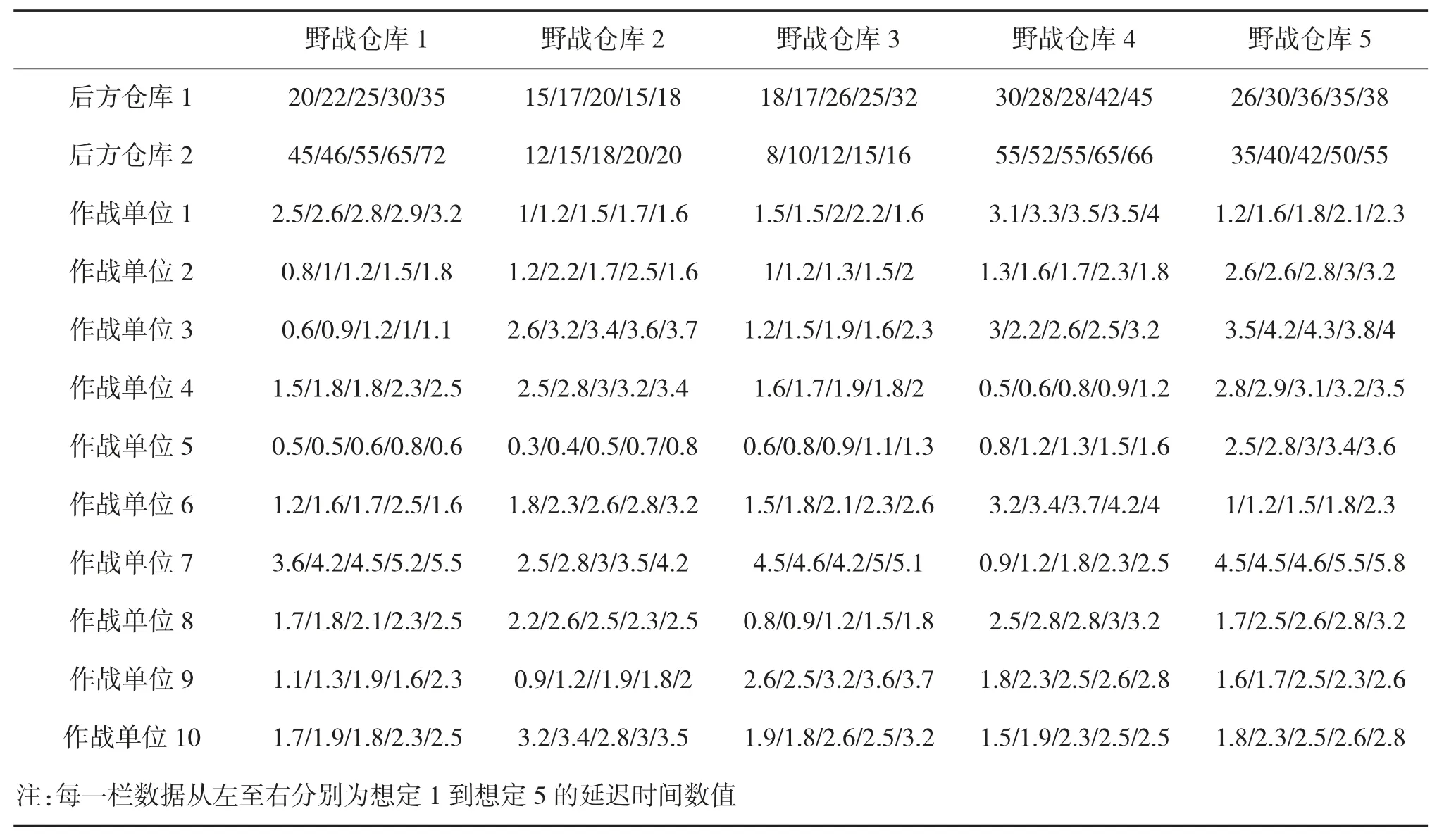
表1 不同想定下节点之间备件供应延迟时间（h）

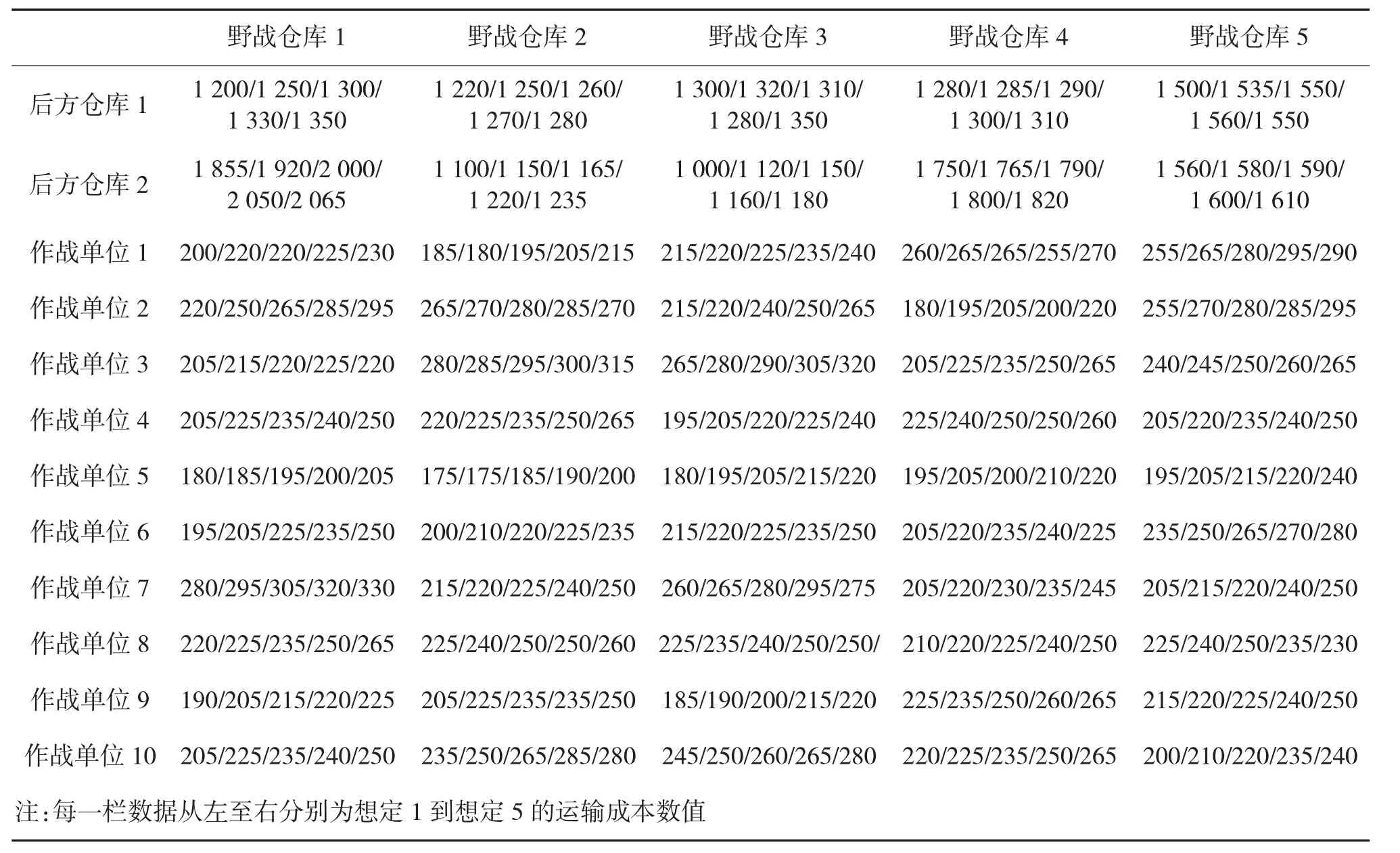
表2 不同想定下节点之间单位备件运输成本（元/个）

表3 野战仓库库存容量和单位库存成本

表4 作战单位备件需求量（个）

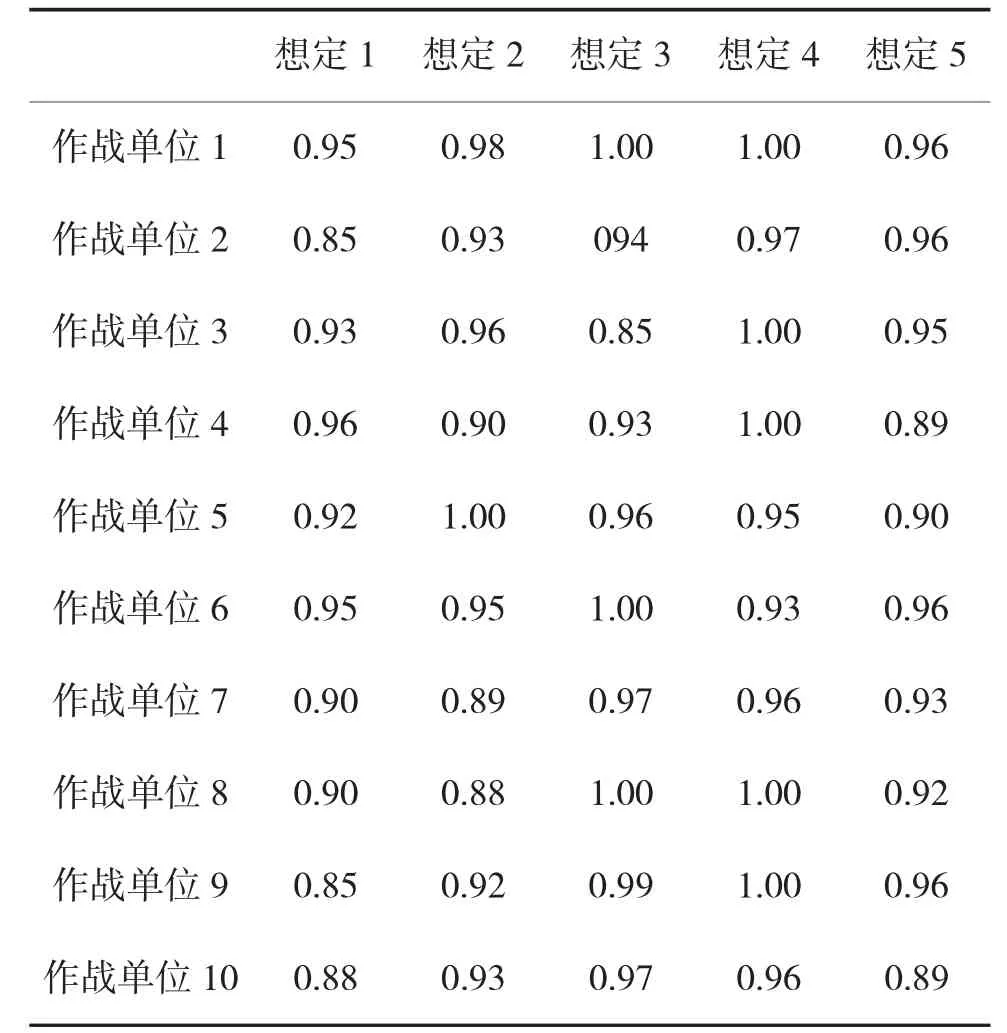
表5 作战单位备件满足率最低阈值

表6 各想定下备件供应总成本最大阈值

4.2 结果分析

分别采用第3 节中4 种变异策略下的差分进化算法对建立的鲁棒优化模型进行求解，结果如图1 所示。图1 中横轴表示迭代次数，纵轴表示鲁棒优化模型式（16）中适应度函数的值。可以发现在第1 400 代时每个算法的优化结果均已基本收敛。其中，DE/current-to-best/1 算法的收敛速度相对较快，且最终的适应度值要小于其他算法。因此，进一步使用DE/current-to-best/1 变异策略下的差分进化算法（以下简称为DE/current-to-best/1 算法）对确定性和鲁棒优化模型进行求解和分析。

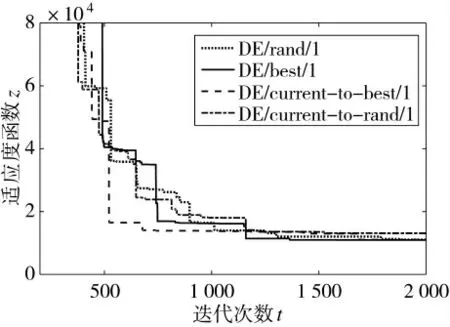
图1 各算法求解结果

4.2.1 想定不确定鲁棒性分析

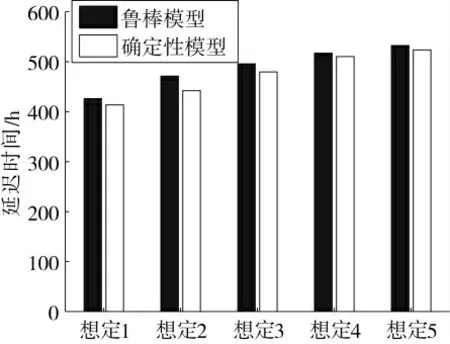
图2 鲁棒优化模型与想定确定模型延迟时间比较

另一方面，将鲁棒优化模型的最优解Vrobust带入各想定下的优化模型，计算总成本和备件满足率两个约束条件以检验鲁棒优化最优解的可行性。同时将各想定下模型的最优解Vs带入其他想定下的优化模型，计算是否满足成本和满足率两个约束。结果见表7，表中√表示解向量完全满足模型约束，为可行解；×表示违反任意约束，为不可行解。从表7可以看出，鲁棒优化模型的解为所有其他模型的可行解，即具有很好的鲁棒性。而各想定下优化模型的解并不能满足其他所有确定性模型。与平时备件供应不同，为确保战斗百分之百顺利进行，战前制定的备件供应方案必须满足所有可能发生的战斗想定的要求。因此，鲁棒优化模型凭借其良好的鲁棒性，更加适合战斗想定不确定条件下备件供应方案决策。

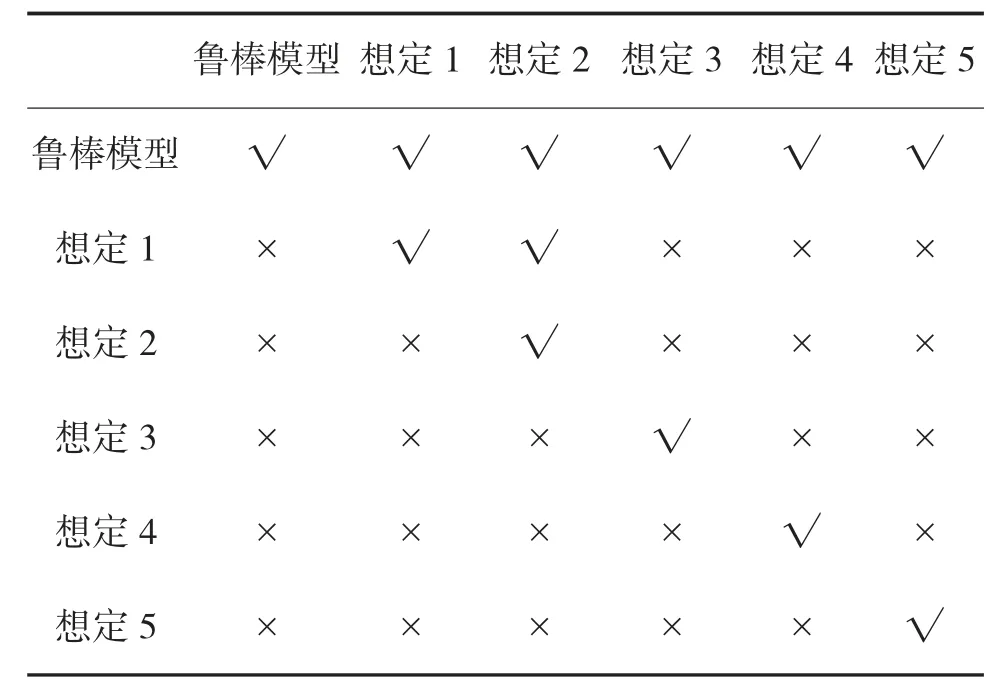
表7 鲁棒优化最优解在各想定中的可行性分析

4.2.2 需求不确定鲁棒性分析

本节主要验证鲁棒优化模型在需求不确定情况下的鲁棒性。由2.2 可知不确定预算参数Γ 主要用来调节模型的鲁棒性和保守性。通过调节Γ 的值可以得到不同不确定程度下的鲁棒优化模型，从而分析需求不确定对备件供应造成的影响。分别取Γ=0、Γ=10、Γ=20、Γ=30、Γ=40、Γ=50。其中，当Γ=0时，备件需求均取名义值，为确定值，称此时模型为名义值模型；当Γ=50 时，备件需求的不确定程度最大，称此时模型为最大值模型；其余情况介于两者之间。图3 给出了Γ 不同取值下的延迟时间。从图中可以看出，需求的不确定性给模型造成了较大的影响。随着需求不确定程度的增加，备件供应的延迟时间也增大。这是由于鲁棒优化模型必须保证满足所有需求取值范围下解的可行性，从而造成模型结果较为保守。

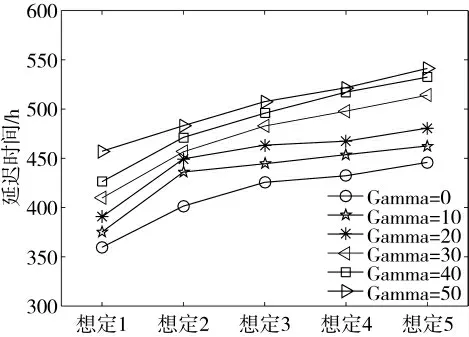
图3 各不确定程度下鲁棒优化模型延迟时间比较

为分析鲁棒优化模型解的可行性，分别比较鲁棒优化模型、名义值模型和最大值模型的约束条件。将各模型的最优解带入其他模型中，检验解的可行性。结果如表8 所示。从表中可以看出，需求不确定条件下的鲁棒优化模型的最优解在其他模型中均为可行解，即能够满足其他需求下的备件供应模型，具有很好的鲁棒性。

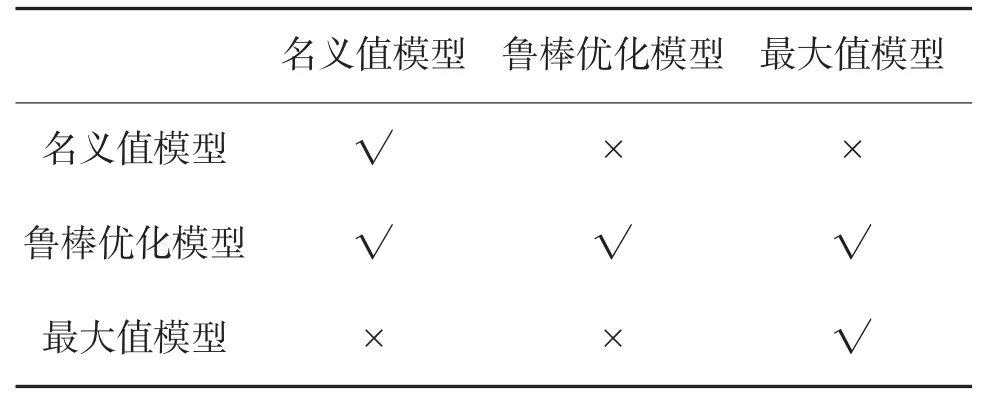
表8 鲁棒优化最优解在各不确定模型中的可行性分析

5 结论

本文考虑战时备件供应的高度不确定性，同时从作战任务想定不确定以及备件需求不确定两个方面进行了鲁棒优化建模。以延迟时间最小为优化目标，以备件满足率和保障成本为约束，构建了战时备件供应的鲁棒优化模型。采用元启发式智能算法对模型进行求解，获得了使得鲁棒优化模型中延迟时间最短的最优解。通过进一步分析发现，鲁棒优化模型的最优解作为任务想定以及备件需求确定条件下模型的可行解。表明鲁棒优化模型在处理战时备件供应的不确定条件时具有良好的鲁棒性。本文建立的鲁棒优化模型，以及求解思路对战时不确定条件下的备件供应优化提供了一定的决策依据和支持。