基于灰狼优化算法的军用运输机航路规划方法

魏燕明，甘旭升，刘 飞，孙静娟

（1.西京学院，西安 710123；2.空军工程大学空管领航学院，西安 710051）

0 引言

军用运输机担负着重要的运输任务，在军事行动中的地位举足轻重。而运输机的航路规划是指在综合考虑各种因素影响的前提下，从航图中规划出起飞和降落机场间的最短航路。在大量航路中，选择科学的规划方法，寻找起点到终点的最短航路，是一个复杂的过程，故可将运输机航路规划问题归结为最短路径问题。

现有航路规划方法通常可归纳为3 类：一是传统方法，例如Voronoi 图法［1］、栅格法［2］等；二是智能优化算法，例如遗传算法［3］、粒子群优化算法［4］等；三是其他算法，例如动态规划算法［5］等。传统算法对障碍物的要求较为理想化，实际地形对规划出的结果影响很大。智能优化算法的特点是不受函数求导的限制，在全局搜索和稳定性方面具有优势，但也存在效率低、速度慢、无法适用动态地图的缺点。其他算法，如动态规划算法，在局部路径上可以达到最优值，也适用于动态地图，但是无法确保全局最优。相比较而言，灰狼优化（Grey Wolf Optimization，GWO）算法［6］能在迭代中通过不断调整收敛因子，实现种群的局部寻优和全局寻优，并通过多个基准测试函数进行测试，从结果上验证了该算法的可行性，并在对基准测试函数的求解精度和稳定性上优于遗传算法、粒子群优化算法与差分优化算法等。因此，GWO 算法在最优无功电力调度、表面波数优化、多输入多输出系统优化、直流电机最优控制、无人机航路规划等工程问题上得到了广泛应用。

鉴于最短路径问题是图论中的经典问题，本文提出基于图论知识构建航空网络，并在此基础上提出了基于一种非线性调节参数的GWO 算法的航路规划方法。

1 基于图论的航空网络模型

航空网络主要有3 种典型网络结构［7］：1）点对点结构。该结构容易设置，但存在航线资源闲置问题。2）线型跳跃结构。该结构的飞机利用率明显提高，其存在飞机频率低、飞机时刻难以安排、规模小等问题。3）轴辐式结构。该结构是指选择流量大、经济发达的城市作为枢纽机场，与其他大中型城市之间设置航空干线，大中型城市与其附近中小型城市之间设置航空支线形成的航空网络模型。当前的航空网络往往是枢纽辐射结构的混合型网络。

考虑到航空网络空间结构整体显现规则网络特征、局部显现不规则特征及核心边缘结构的特点，本文采用图论的相关知识，对特定区域航空网络的拓扑结构进行描述。由此，建立基于图论的航空网络模型共分为以下3 个步骤［8］：

1）网络节点的确定。在构建航空网络模型时，通常把机场作为网络节点。2）确定边权。将两机场之间的距离作为边权。3）建立邻接矩阵，绘制航空网络模型图。

2 运输机的航路规划问题

军用运输机的航路规划就是在一定条件下最短路径的求解问题，主要有Dijkstra 算法［9］和Floyd算法［10］等，这两种算法是当前较为成熟的求解最短路径的方法，但是这两种算法求解速度较慢，历时较长，并不适合军用运输机的航路规划问题，因此，本文试图探索一种更快求解军用运输机航路规划问题的方法。

2.1 目标函数

通常情况下，军用运输机的航路规划问题主要考虑以下3 个因素：

1）距离。对于航路规划问题，距离因素最重要。从航空网络模型可以看出每个航线点之间的距离，没有航线的航线点之间用0 表示。由于距离的数值较大，如果使用这一数值，其他约束条件的影响将会微乎其微，所以要对所有参数进行统一。在真实数据的基础上，将距离的数值限定在（0，1］之内，故其表达式为

式中，S 为距离约束条件，s 为两航线点间的真实距离，max 为航线点间的最大距离。

2）天气。由于天气因素对飞行有较大影响，在解决航路规划问题时一定要考虑天气因素。天气较为复杂，本文将天气分为：对飞行没有影响（记为0）、对飞行影响较小（记为0.2）、对飞行影响适中（记为0.5）、对飞行影响较大（记为0.8）、对飞行影响很大（记为1）。在求解过程中，上述5 种情况随机产生，记为t。当t=1 时，天气对飞行器飞行的影响很大，为避免天气因素影响飞行，在规划航路时，就不能经过这一导航点。

3）飞行器密度。航线上能承载的飞行器数量是有限的，当航线上飞行器过多时，可能导致飞行器间的距离过近，引发飞行事故。所以，在解决航路规划问题时，一定要考虑航线上的飞行器密度ρ=x/N，其中，x 为航线上已有飞行器数量，N 为航线承载飞行器上限。当ρ=1 时，航线上飞行器密度对飞行影响很大，易引起相撞，为防止相撞，规划航路时，就不能经过该导航点。

根据不同因素对航路规划的不同影响程度，对考虑的不同因素进行加权，当ti≠1 且ρi≠1 时

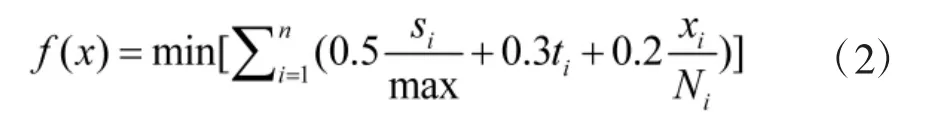
根据以上表达式，对GWO 算法求解航路规划问题的权值进行重新规划；当ti=1 或ρi=1时，这一导航点不能使用。

2.2 约束条件

在运输机的航路规划过程中，存在限制整个规划的约束条件［11］。具体包括：

1）油耗。运输飞机载物时由于其最大起飞重量的限制、跑道承重限制以及最低空载重量的限制，燃油的携带量都是经过精准计算。要根据具体油量来规划合理的飞行距离；

2）任务时间要求。运输飞机必须在规定时间内完成运输和支援任务；

3）航路距离。飞行的航路距离必须少于同等负重条件下的运输飞机的最大飞行距离，受到燃油限制和飞行时间限制；

4）途经点。在执行飞行任务时必须飞过的一些航路点。

出于简化问题需要，本文没有考虑禁飞点、地形的限制以及飞机自身性能的限制。

3 灰狼优化算法

根据前面对军用运输机航路规划问题的分析，可知该问题是一类多约束、非线性复合最优化问题，其难点在于对约束条件的处理，尤其是对任务约束的处理，而GWO 算法由于采取领导层级机制，在处理约束条件时，不与适应度函数直接关联，能够有效解决多约束问题，并且不影响算法的寻优性能［12-13］。虽然GWO 算法得到了广泛的应用，但也存在收敛速度不高、全局搜索能力弱、易陷入局部最优的缺点，据此，本文针对所建模型的具体特点，引入一种非线性调节参数增强其全局搜索性能和精度。

3.1 标准算法

灰狼处于自然界中食物链的顶端，喜欢群居生活，并且具有严格的社会等级制度，将群体划分为4个等级，呈金字塔结构，处于顶端的为领导层，称为Alpha（α）狼，它是整个灰狼群体的核心，对捕食、休整等问题拥有决策权；第二级为Beta（β）狼，主要辅助Alpha（α）狼作决策，并负责向下加强贯彻该决策；第三级为Delta（δ）狼，负责贯彻执行Alpha（α）狼与Beta（β）狼的决定，并且担负警卫、照顾受伤灰狼和幼小灰狼的任务；处于底层的为Omega（ω）狼，主要跟随前3 个层级的狼捕食和休整。具体捕食时，灰狼群体在Alpha（α）狼的带领下，搜寻猎物并逐渐接近，待确定猎物具体位置后，形成包围圈并逐渐缩小，最后实施攻击。

为了模拟灰狼的捕食机制，以解决问题的优劣程度来模拟划分灰狼的社会等级，最佳解决方案视为α 狼，第2 和第3 最佳解决方案分别命名为β 狼和δ 狼，其他解决方案均被假定为ω 狼。

在GWO 算法中，设定灰狼包围猎物时，灰狼与猎物之间的距离为

3.2 改进策略

由前述可知，基于航空网络的航路规划能否满足约束条件，直接关系到任务的成败，目前对约束处理的方法主要有特殊算子法［14］、随机排序法［15］、可行性准则［16］和惩罚函数。而惩罚函数的方法简单、复杂度低，适用于多种优化问题，故采用惩罚函数来处理模型中约束。当满足约束条件时，则惩罚因子为0，否则令其为负无穷。

3.3 算法优化流程

在航空网络基础上实现军用运输机的航路规划，采用改进灰狼算法优化计算步骤如下：

1）明确目标，对航空网络内的飞行路径进行编码；

2）设定种群数目N、最大迭代次数tmax、维数以及上下界；

3）初始化种群、根据适应度函数及约束条件，找到最优的前3 个计算备选解，令t=1；

5）按照式（8）～式（10）与式（14），更新各个灰狼个体的位置；

6）令t=t+1；

7）适应度函数计算每个灰狼个体的适应度值，保存最优的前3 个计算备选解，判断是否达到最大迭代次数，若是，则算法结束，输出最佳飞行路径，否则返回第4 步；

8）输出所规划的航路。

4 仿真分析

4.1 人造网络的航路规划

首先，使用较为简单的人造网络对算法进行验证，如图1 所示。改进GWO 算法的参数设置：初始种群个数为50，最大迭代次数为50，c1=1，在Matlab2014a 上运行50 次。

图1 人造网络

该人造网络有15 个节点，27 条连边，每条连边长度如上图。该人造网络的带权邻接矩阵为

通过GWO 算法求解人造网络中节点1-节点11 的最短路径，结果如下页图2 所示。可以看出，用GWO 算法求解最短路径，结果收敛很快，当迭代到第21 代时，结果稳定，不再变化，最短路径长度为6。仅考虑权值，得到仿真结果如表1 所示。

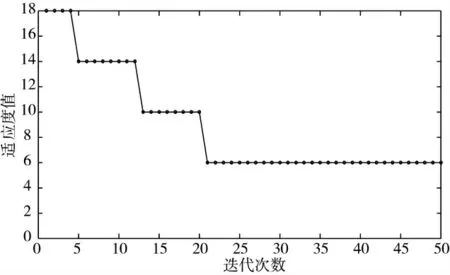
图2 GWO 算法求解结果

表1 求解结果对比

当使用GWO 算法求解从1-11 的最短路径时，首先得到的是距离18，路径为1-3-6-10-9-12-8-11，继续迭代得到距离为14，路径为1-5-14-12-8-11，继续迭代得到距离为10，路径为1-5-14-11，继续迭代得到距离为6，路径为1-5-8-11，继续迭代结果不变表明，1-11 最短路径为1-5-8-11，距离为6。

不难看出，通过GWO 算法求解最短路径得出的答案和Floyd 算法、Dijkstra 算法求解得到的答案是一致的，利用其求解航路规划问题是可行的。

4.2 北京地区航空网络的航路规划

通过人造网络的求解已经得到了GWO 算法求解最短路径的可行性及可靠性，下面在以北京为枢纽的航空网络模型229 个节点的基础上，使用GWO算法，求解以北京为起点的某两个网络节点间的最短距离及最短路径。表2 为截取的部分节点连通情况及节点间距离。

通常情况下，机场在短期内不会增加或减少，数量比较稳定，而飞机有可能取消、延迟，并不稳定，并且导航台是固定在地面上的，不能移动。出于阐述问题需要，先以10 个有通航关系的导航台为网络节点。这些导航台分别为：大王庄VOR 量（VYK），DOGAR，LADIX， 天 津 NDB（CG），P75，KALBA，PAMDA，ANRAT，IKENU，衡水NDB（HG），并分别表示为节点a，b，c，d，e，f，g，h，i，j。然后以两个节点之间的距离作为边权，进而得到如下的带权邻接矩阵

对于以北京为枢纽的航空网络包含229 个节点，其带权邻接矩阵比较庞大，在此基础上对军用运输机进行航路规划，其求解过程如下页图3所示。

表2 以北京为枢纽的航空网络节点

图3 GWO 算法求解结果

从图中可看出，用GWO 算法求解最短路径，收敛很快，当迭代到第95 代左右时，结果基本稳定，不再变化，这时节点连成的路径，即为最短路径，路径长度即为最短距离。表3 为综合考虑距离、天气、航路上飞机密度等因素时，GWO 算法、Dijkstra 算法和Floyd 算法得到的结果的对比。

由表可以看出，在综合考虑距离-天气-航空器密度等因素后，由于天气和飞行器密度的影响，有一些距离较近的导航点不能使用，需考虑其他导航点。以北京到南阳为例：紫石口（RENOB）导航点因天气原因不能使用，Dijkstra 算法和Floyd 算法时，只考虑距离因素，没有考虑其他因素，得到的航路距离较短，但还是无法使用。而用GWO 算法求得的距离，相较于Dijkstra 算法和Floyd 算法的求解距离略大，不过由于考虑因素相对全面，能更好地进行航路规划供军用运输机使用。

表3 求解结果对比

5 结论

现代战争对军用运输机的航路规划的要求越来越高。本文在航空网络基础上，采用GWO 算法对航路规划进行了研究。主要得出如下结论：

1）基于图论相关知识构建了航空网络模型，收集相关数据，为后续的建模求解做铺垫。2）在已构建航空网络基础上，提出基于GWO 算法的军用运输机航路规划方法。结果表明GWO 算法用于军用运输机航路规划问题是可行的，能够很好地完成军航航路规划的求解。3）采用本文方法对北京地区航空网络节点间最短路径求解，并与Dijkstra 算法和Floyd 算法进行比较，验证了方法的实用性和有效性。4）在未来的研究中，可考虑更多的对军用运输机飞行有影响的因素，重新建立目标函数，以科学、合理地进行航路规划。