变幂次趋近律的滑模制导在防空反导中的应用*

穆忠伟，吴 剑，韩秀枫

（南昌航空大学信息工程学院，南昌 330063）

0 引言

精确制导技术是现代高科技武器发展的新趋势。近年来，美军多次运用“震慑”战略思想，实施不接触战术，采用“精确打击”武器对敌方雷达、桥梁、机场、坦克、车辆、船舶等固定与活动目标实施“点穴”式精确打击，有效地保存了有生力量，沉重地打击了对手，为赢得战争的最后胜利起到了决定性的作用［1］。从而研究如何反导对于防御敌方导弹的威胁与破坏至关重要，尤其是针对敌方机动性目标，对己方的威胁程度大大提高，如何快速并灵活地响应打击机动目标的制导律显得尤为迫切。

由于滑模变结构控制是一种抗干扰性、鲁棒性强、响应灵活的非线性控制方法［2-8］，被广泛运用于制导控制领域，尤其目前越来越多的学者研究其滑模趋近律，以提高导弹在拦截制导中的快速响应能力。文献［9］采用自适应滑模趋近律的变结构制导律，以实现攻击机动目标的任务；文献［10］利用指数趋近律的方法来实现趋近滑模面的过程中，提高导弹攻击目标的响应能力；文献［11］针对拦截机动目标问题，采用双幂次趋近律，使导弹收敛速度增快。

为了进一步提高导弹的快速响应能力及抵消抖振问题，本文提出了基于变幂次趋近律变结构制导律，提高了导弹在打击机动目标的响应能力，并有效地规避抖振问题的产生，并利用干扰观测器对目标的机动加速度进行观测和估计，从而使制导律性能进一步提高。

1 弹目相对运动关系

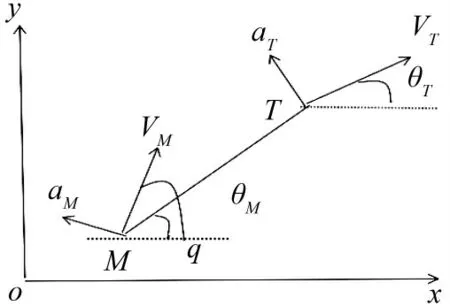
图1 导弹与目标的相对运动关系

导弹在防空反导的末制导段拦截攻击目标，如图1 所示弹目的相对运动关系，M 表示导弹，T 表示目标，VM和VT均为常量，将M 和T 之间的相对距离设定为R，q 为弹目LOS 角，aM和aT为导弹与目标的法向加速度，θM和θT均为各自的弹道倾角。设各个角度逆时针方向为正，末制导的运动学关系为

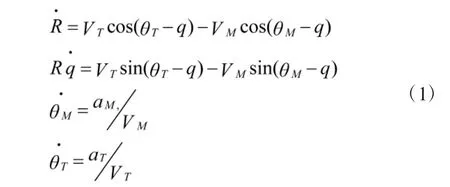
将式（1）中的第二式两端求导可得：

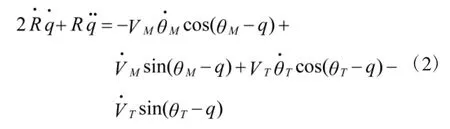
由式（2）进一步得出：

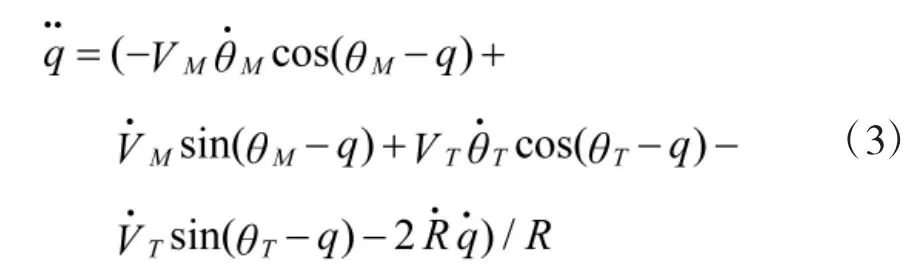
将拦截弹成功拦截目标处的夹角定义为终端LOS 角qf［12］，为建立状态方程，下面取

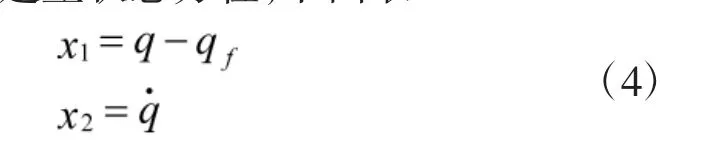
可得：

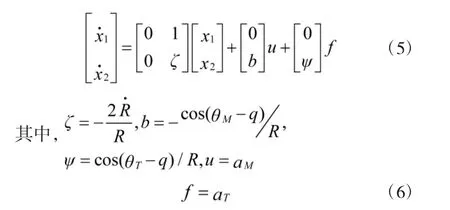
其中，a 为机动加速度，将f 视为有界干扰。

2 基于变幂次趋近律的制导律

2.1 构造滑模面

首先构造滑模面

式中，σ＞0，k1＞0。

下面对式（6）两端求导可得：

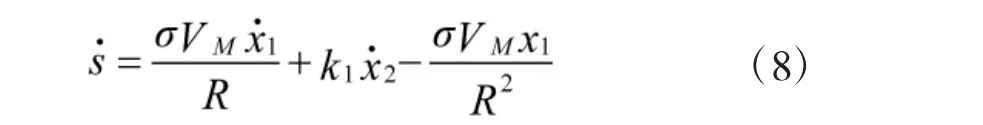
2.2 趋近律的对比

新型变幂次趋近律、传统变幂次趋近律与双幂次趋近律作对比［15］如下：

双幂次趋近律［13］的表达式为：

其中，δ1＞0。

下式为新型变幂次趋近律［15］的表达式：

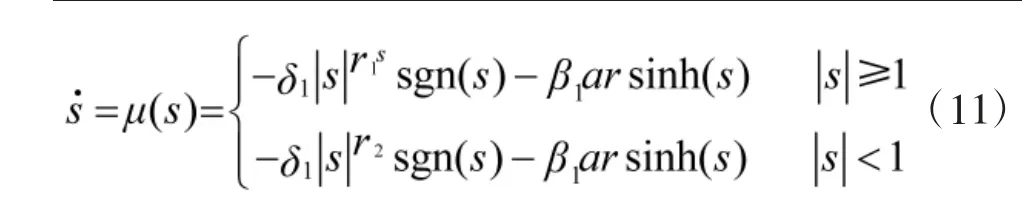
其中，β1为正数，ar sinh（·）是反双曲正弦函数。

证明：令滑模函数的初始状态均为大于1 的数，将系统轨迹趋近滑模面s=0 的过程分为两个阶段，一个是从初始状态s0距离滑模面为1 的位置，另一个是与滑模面距离为1 的位置到滑模面。

2.3 制导律设计

结合式（5）、式（7）、式（11）

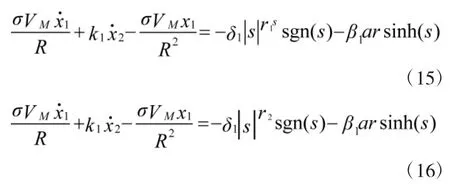
由式（15）、式（16）推导出制导律为：

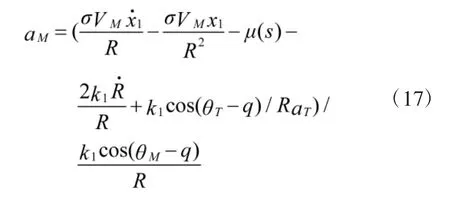
由于式（15）、式（16）中存在着符号函数sgn（s），其会使系统轨迹在运动过程中出现较大的抖振现象，为消除抖振的问题，利用饱和函数式（18）代替符号函数。

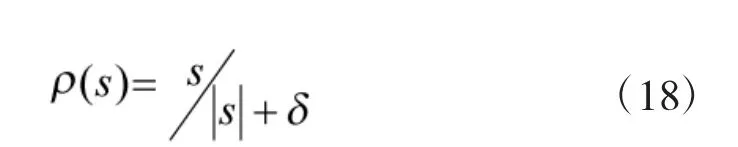
2.4 滑模观测器设计

3 仿真算例

以某型导弹在末制导段拦截目标为例，拦截弹的初始条件为xM（0）=0 m，yM（0）=3 500 m，导弹的初始飞行速度vM=650 m/s，初始弹道倾角θM（0）=0；目标的初始坐标位置为xT=2 000 m，yT=1 000 m，目标的初始飞行速度vT=350 m/s，初始弹道倾角θT=π/3；制 导 律 参 数 σ=400，k1=5，δ1=1.6，r1=2，r2=3，β1=6，δ=300。设目标的机动为aT=-100cos（0.5πt），L=110，w0=0.1。

算例1 目标以匀速飞行不做机动，拦截期望角度分别为-30°和-45°。

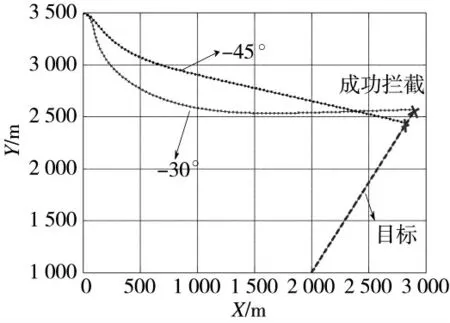
图2 拦截弹道

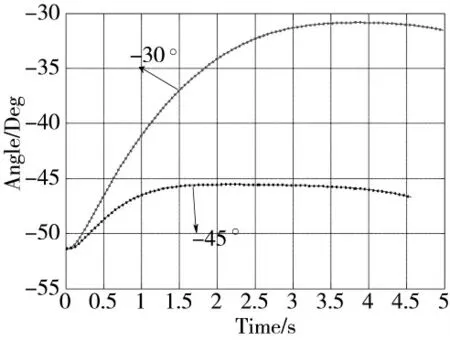
图3 视线角变化曲线

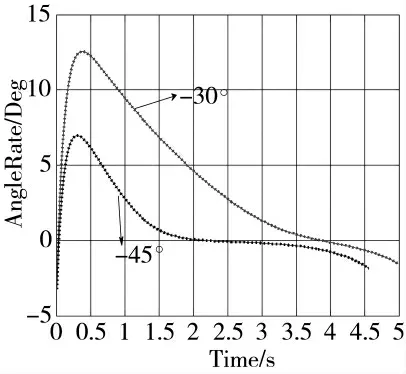
图4 视线角速率变化曲线

由图2 可知，拦截弹分别以-30°与-45°拦截目标，最终都以平滑的弹道成功拦截目标，但以-30°拦截目标的弹道开始弯曲较大，要改变其弹道，最终以平直的弹道成功拦截目标。

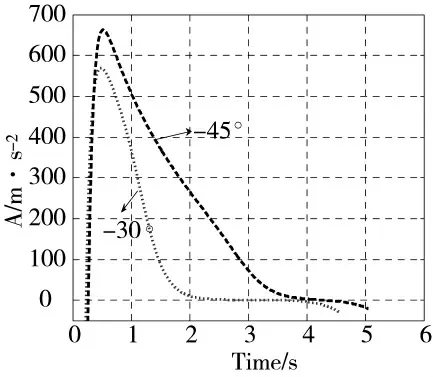
图5 过载曲线

由图3 及图5 可知，导弹在以-30°做机动飞行时，其改变的机动过载要大于后者，飞行时间要比较长，在末端拦截时，都以相应的角度收敛于期望角。由图4 可知，拦截弹开始时，变化比较大，而后最终以很快的速度收敛于0 附近，拦截弹最终以最小脱靶量命中目标。

算例2 目标以余弦机动做飞行，拦截期望角度分别为-30°和-45°。

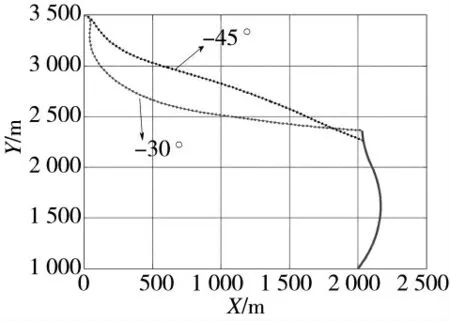
图6 弹道曲线

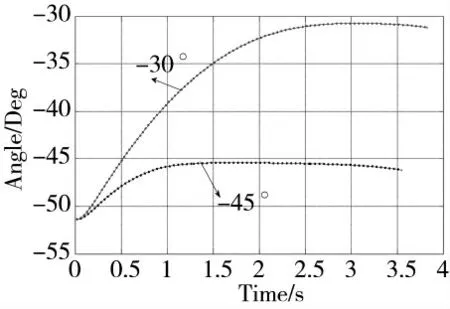
图7 视线角变化曲线

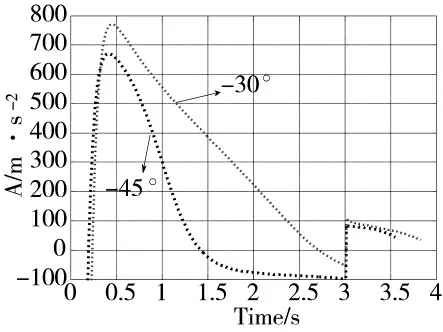
图8 过载曲线

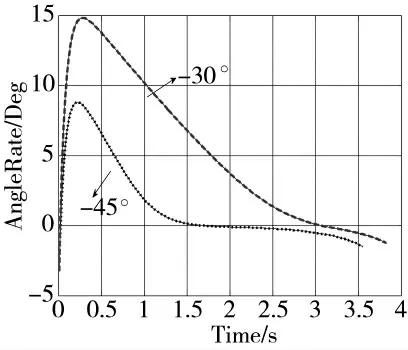
图9 视线角速率

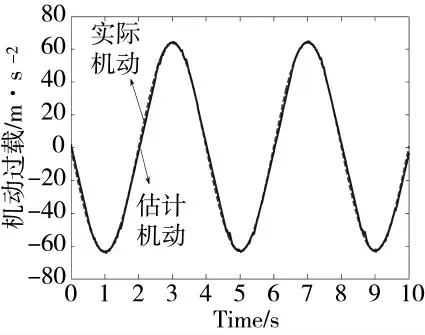
图10 目标机动估计

由图6 和图8 可知，由于目标做机动，拦截弹分别以-30°与-45°均以稍微弯曲的拦截弹道拦截目标，做较大的机动以适应对机动目标的跟踪，并在接近目标附近时，机动变化较大，以拦截目标；由图9 知，导弹在接近目标附近时，视线角速度更小，变化更加平稳，最终会对于减小末端脱靶量具有极大的优势；图10 是基于滑模观测器的目标机动估计，在整个末制导过程，观测及跟踪目标的实际机动，保证了目标机动的补偿，从而有利于导弹成功捕获目标并拦截。

算例3 与传统指数趋近律的制导律进行对比，拦截期望角度为-45°。

与传统指数趋近律对比，传统的指数趋近律为

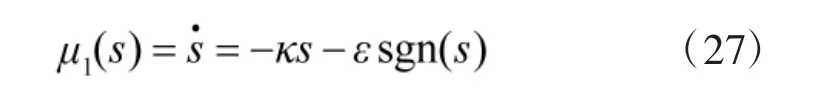
其中，系数κ、ε 均为正数。κ=5，ε=2，由于式（27）中存在符号函数sgn（s），趋近律的切换项中含有符号函数会导致系统的状态轨迹在滑模面s=0 附近反复振荡，产生比较大的抖振，代入式（18）饱和函数以减少抖振，从而传统指数趋近律的导引律如下：

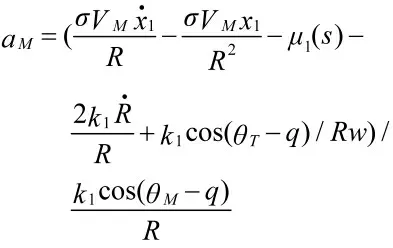
由图11 两者的拦截弹道对比，最终都成功拦截目标，本文制导律的拦截弹道以稍微的弯曲拦截目标。由图12 及图13 可知，变幂次导引律以更快的速度收敛于期望角度，加速了导弹以特定角度跟踪目标，从机动过载来看，变幂次比传统指数的机动变化要大得多，对于跟踪机动目标具有更大的优势；由图14 可知，变幂次导引的视线角速度收敛的速度比后者要更快地收敛于0，以保持对拦截目标的最大优势。

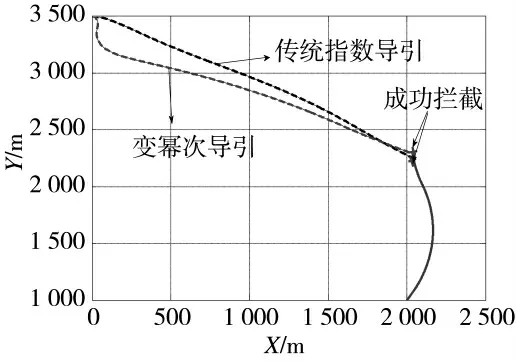
图11 拦截弹道对比

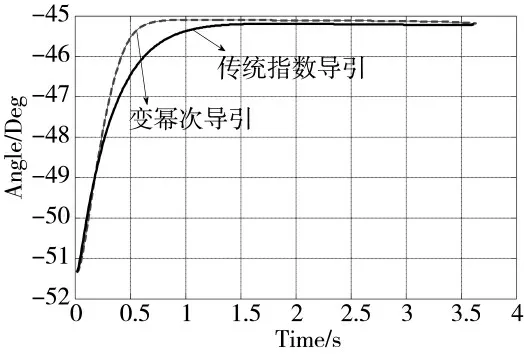
图12 视线角变化对比

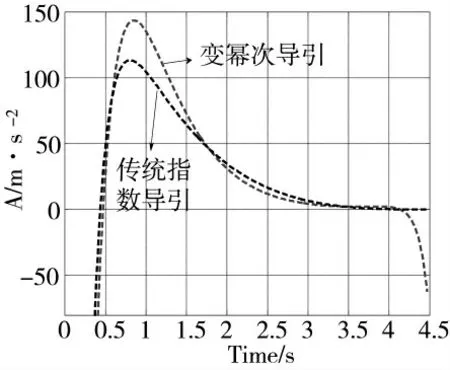
图13 过载曲线对比

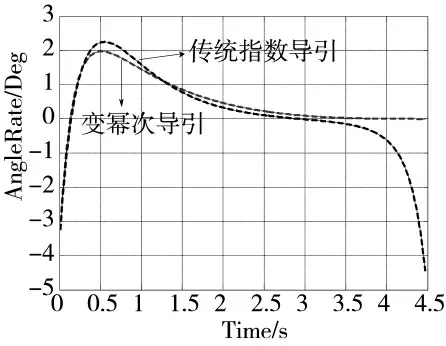
图14 视线角速率对比

4 结论

本文基于变幂次趋近律具有使系统轨迹的滑模动态收敛速度快的优点，提出了采用新型趋近律的滑模制导律，针对目标做机动的情况，设计了滑模观测器对其机动估计，在制导律中加入补偿，并对变幂次趋近律的收敛时间与其他传统趋近律进行比较并证明，通过与传统指数趋近律的导引律进行对比，仿真显示，设计的制导律在末端反导拦截的飞行中，所收敛的视线角及其角速度的时间要比后者更快，在实战中具有更好的制导性能。