堰塞坝溃决模拟研究综述与展望

段文刚，黄 卫，魏红艳，戴盼伟

（长江科学院 水力学研究所，武汉 430010）

1 研究背景

由地震、暴雨诱发的崩塌、滑坡堵江形成的堰塞坝通常由松散土石堆积而成，绝大部分存在水流漫溢溃决的危险［1-2］。我国有记录的堰塞湖超过400个，约85%发生在长江上游及西南诸河。当前，在地震、气候变化和人类活动多重影响作用下，堰塞湖溃决事件发生频次显著增加。仅以2018年为例，金沙江和雅鲁藏布江就发生了4次大型堰塞湖溃决事件。堰塞湖一旦溃决将形成极端洪水，如2000年西藏易贡堰塞湖溃决洪水最大瞬时流量达120 000 m3/s；2008年唐家山堰塞湖溃决洪水峰值流量达6 500 m3/s（见图1（a）），远大于该河段历史实测最大洪峰流量4 270 m3/s；2018年白格堰塞湖溃决洪水峰值流量达到33 900 m3/s（见图1（b）），远超金沙江上游河段万年一遇洪峰流量10 600 m3/s，严重威胁下游人民生命财产和工程安全。

图1 唐家山和白格堰塞湖溃决Fig.1 Landslide lake breaching of Tangjiashan and Baige

堰塞坝溃决过程与溃决洪水演进预测是堰塞湖灾害风险评估、人员避险转移和应急处置方案制定的理论基础。如何快速准确地预测溃坝洪峰流量及其演进过程是堰塞湖应急处置的关键。这里存在以下关键科学问题：①堰塞坝何时溃决？②堰塞坝溃决机理、溃决历时、溃口断面及其发展过程。③溃口峰值流量多大？④溃坝洪水演进特性。溃坝洪水何时以何流量到达下游城镇或居民点、水利水电工程、交通桥梁设施等？只有尽可能准确地模拟堰塞坝溃决过程，才能更准确地预测溃口洪峰流量，进而对下游洪水演进准确预测。堰塞坝溃决过程与其几何形态、颗粒粒径级配、内部结构、密实度、库容和上游来水等密切相关，溃决机理复杂，预测难度极大。鉴于堰塞坝溃决过程模拟和溃决洪水预测的复杂性，加上缺乏应急处置现场资料，为安全保险起见，溃坝洪水分析预测的峰值流量通常较实际偏大较多，以致“防卫过当”造成不必要的社会损失和财产损失。因此开展堰塞坝溃决研究具有重大现实意义。

2 研究进展综述

堰塞坝溃决研究涉及水力学、土力学、泥沙运动力学、河床演变学等多门学科，近年来一直是国内外学者关注的焦点。由于堰塞湖形成的特殊性和复杂性，目前对堰塞坝溃决过程和溃决机理的认识尚不成熟，研究成果有限。堰塞坝与土石坝存在一定程度的相似性，而土石坝溃决过程和机理的研究成果较为丰富［3-11］，因此基于土石坝溃决过程的认识可为堰塞坝溃决研究提供借鉴。同时，堰塞坝组成物质多为非黏性颗粒，粒径级配分布宽而不均匀，结构松散、坝体密实度差，且不均匀性强；坝体无防渗体，渗漏相对较大；坝体顺河向长度较大（如白格堰塞坝顺河向长2 km），坝坡较缓；等等。这些不同之处也决定了其溃决过程与人工土石坝存在差异。

当前堰塞坝溃决研究主要采用试验研究和数值模拟方法。

2.1 堰塞坝溃决试验研究

水槽试验主要研究堰塞坝溃决机理，这方面研究成果相对丰富。Yan等［12］在长80 m、宽1.2 m、深0.8 m的水槽中，采用松散堆积体模拟堰塞坝在上游来流作用下发生漫溢溃决，结果表明上游流量和坝体组成是决定溃决过程的关键因素。张婧等［13］对坝高0.3 m、坝宽0.5 m、背水坡比1∶2～1∶4的堰塞坝开展了试验研究，结果表明堰塞坝溃决与土石坝的陡坎侵蚀有明显区别，同时提出了堰塞坝溃决4个发展阶段的特征，并表明背水面坡度和坝体级配会影响洪峰流量及峰现时间。邓明枫等［14］对坝高0.3 m的堰塞坝开展试验研究，分析认为漫顶冲刷破坏是水流运动时产生的剪应力超过土体的抗剪强度所造成的，水流运动时的剪应力包括流速剪应力和陡坎剪应力，它们分别侵蚀土体并使溃口在横向和垂向上发展。冲刷破坏包含土粒间剪切和孤粒搬运2个过程，2个过程互为补充。堰塞坝溃决过程中，水流的冲蚀作用主要表现为表层冲刷，堰塞坝在水流作用下沿河流运动方向的坡角也逐渐减小，这与黏性土坝在溃坝水流作用下的“陡坎”冲蚀具有明显区别。刘磊等［15］在长15 m、宽0.6 m、深0.9 m的水槽中开展了堰塞坝溃决试验，对入流流量、坝体坡度、坝顶宽度和坝顶高度4个主要影响因素进行了研究，发现：入流流量和坝顶高度对泄流过程影响较大且与洪峰流量成正相关关系，但坝顶高度的增加会导致峰现时间的延后；减缓坝坡和增加坝顶宽度都能减小冲刷速率，从而起到加固坝体的作用，同时可以降低洪峰流量并延长峰现时间。Zhou等［16］在长45 m、宽0.7 m、深1.5 m的水槽内开展了堰塞坝试验，结果表明在快速溃决过程中，土壤侵蚀率与剪切应力呈线性关系，同时水流土壤侵蚀阻力随着含沙量沿程增加会不断加大。

调研得知，现有水槽试验坝高0.3～0.8 m，坝宽0.5～1.2 m，总体尺度较小。试验得出的部分结论与实际库容较大的堰塞湖溃决过程相差甚远，主要是因为试验未模拟足够大的库容而出现的不相似结果。

目前，堰塞坝溃决研究对于是否会出现黏性土坝常见的“陡坎”冲蚀模式并没有一致认识。事实上，“陡坎”冲蚀形成与堰塞坝粒径级配、下游坝坡坡度和密实度等有关，至于何种边界条件出现“陡坎”冲蚀仍值得深入研究。如果不是“陡坎”冲蚀模式，控制溃口流量的就不是宽顶堰流，而是明渠水流，这可能是对当前数学模型假设的最大颠覆，科学意义重大。此外，堰塞湖库容大小直接决定了库水位下降速度，进而决定了溃口发展速度和最终溃口形态，最终导致溃口峰值流量变化。段文刚等［17］对坝高1.0 m、坝宽2.0 m、下游坝坡坡比1∶3、库容60 m3的土石坝开展试验研究，揭示了土石坝漫溢溃决物理过程4个阶段（见图2）：下游坡面侵蚀沟发育阶段（侵蚀过程缓慢）、下游坡面多级跌坎冲刷阶段（冲蚀能力渐大）、“陡坎”冲蚀阶段（坝体快速坍塌）、坝体冲蚀趋于稳定阶段。应该指出的是，由于试验库容较小，坝前水位降落过快，坝体横向尺度较小，未能模拟显示最终溃口形态，导致溃口峰值流量和“陡坎”冲蚀以后的溃决过程与实际偏差较大。

图2 土石坝溃决过程试验Fig.2 Tests of breaching processes of embankment dam

张红武等［18］提出堰塞坝溃决物理模型设计除应考虑几何相似和水量相似外，还应满足重力相似、水流阻力相似（针对下游河道）、水流运动相似、沙石起动相似和泥石流流速相似共5个方面。并为复演唐家山堰塞湖漫顶溃决的三维变化特征，开展了几何小变率模型试验研究。模型水平比尺λL＝280，垂直比尺λH＝240，模型坝体材料级配采用中值粒径D50＝0.1 mm的天然沙并混掺1/8的小砾石（粒径2～10 mm）配成。

应该指出的是，IMPACT Project、美国农业部和南京水利科学研究院针对土石坝开展了多次大尺度现场溃决试验［19-21］，并且不同尺度的土石坝试验溃决机理和溃决过程确实存在着一定差异。直接针对堰塞坝溃决的大尺度试验成果尚不多见。

通过对堰塞坝溃决水槽试验的总结，加深了对其溃决机理的认识。需要指出的是，不同学者揭示的堰塞坝溃决机理还有差异，关键影响因素认识还不完全一致，这表明当前对堰塞坝溃决机理的认识仍不成熟。因此需要开展大尺度溃决试验，对堰塞坝溃决机理进行深入研究。

2.2 堰塞坝溃决数值模拟

堰塞坝溃决数学模型有统计模型、参数模型和物理过程模型［22-23］。近年来主要发展的是基于参数的数值模拟和基于物理过程的数值模拟。基于参数的模型是建立在统计分析溃坝历史资料基础上的统计模型，已有的相关模型中主要采用坝高、库容、溃决时库水位与溃口高差等作为特征参数，建立最终溃口宽度、溃决时间和洪峰流量的模型表达式［2，24-25］。但是，堰塞坝溃决案例实测资料稀少且难以获得，因此统计资料的选用具有较强的主观性，导致该类统计模型的计算结果往往存在较大的不准确性［26］。同时，该类模型只能计算出洪峰流量、溃口最终宽度和峰现时间等离散值，无法得到这些参数的时变连续变化值。现有模型对最为关键的溃口冲刷速率还主要采用定性描述［27］，从而带来较大不确定性。

基于物理过程的数学模型是依据堰塞坝溃口发展机理，从理论角度考虑了水流运动、泥沙输移、边坡稳定性等因素而建立的能预测溃决过程及下泄洪水过程的模型。当前堰塞坝溃决研究中，原本针对土石坝溃决的模型仍然得到沿用［28］，本文称为土力学方法。Cristofano［29］于1965年最早提出了模拟土石坝漫顶溃决时变过程的数值模型，Harris等［30］在此基础上建立了HW模型。随后，Fread［31］开发了BREACH模型，该模型采用2种模式计算溃口展宽及形状变化过程：一种模式是假设溃口形状为矩形，发展变化形式同DAMBREAK模型；另一种模式是通过坝体材料的特性确定临界滑裂面，当溃口深度超过临界深度时边岸以临界角度发生崩塌。这类模型结构简单并且考虑了溃口发展过程，因此被广泛应用于行业软件中。模型能够反映溃决过程的物理细节，有可能真实再现或准确预报溃决洪水过程，因此近年来发展较快，一些学者建立了比较新的基于物理过程的模型。黄金池［32］将堰塞坝溃口展宽过程分为溃口垂向下切、侧向展宽和溯源冲刷3种形式，建立了堰塞坝渐进溃决的数学模型。朱勇辉等［33］以土石坝溃决模型为基础，溃口展宽采用土石坝渐进溃决的溃口发展模式，建立了堰塞坝渐进溃决数学模型，并对唐家山堰塞坝进行了模拟计算。Chang和Zhang［34］针对唐家山堰塞坝坝体材料垂向分布不均匀，开发了考虑侵蚀度沿垂向变化的溃口发展模型。钟启明等［35］基于水槽冲蚀试验结果提出了可以反映坝体材料特性及水流特性的土体冲蚀公式，以此建立了描述堰塞坝漫顶溃决过程的数学模型，并通过唐家山堰塞坝实测资料验证了其合理性。

应该指出的是，土力学方法模型引入了大量的人为假设。其中：第1个假设为溃口流量采用宽顶堰公式计算。由于天然堰塞坝顺流长度一般都远大于人工坝体，并且溃口尺寸沿程是变化的，宽顶堰公式的适用性值得怀疑，并且采用宽顶堰公式也无法重现土石坝中常见的喇叭形状溃口特征［36］。第2个假设为在溃决中保持边坡坡度不变。对于松散堆积体而言，边坡在水流作用下会发生冲刷，并且坡度不断变陡，直到超过临界坡度时发生坍塌。第3个假设为部分模型还需人为给定残留坝高以控制冲刷终止高程。实际上冲刷终止高程应该是由土体性质和水流条件共同决定的，当水流强度不足以冲刷土体时，溃口就停止冲刷下切。由于这类模型引入了过多的假设，并且部分参数的假设只是基于经验并无坚实的物理基础，即使通过参数调整对水槽试验或具体实际案例溃决过程进行了较好的复演，在相关参数物理意义和影响规律完全弄清楚之前，这类模型的预测精度仍然没有保证。同时，这类模型不具有同时模拟溃口发展过程、堰塞湖湖区水动力条件和下游洪水演进及河床变形过程的能力，即全场模拟。对于湖区而言，湖区水流是运动的，具有一定的水面梯度，因此采用水量守恒方式得到的坝前水位与实际水位是有差异的。同样地，对于下游河道而言，溃口发展过程中的水流泥沙将引起下游河床的剧烈冲淤变化，进而会对不同阶段溃口发展过程和下游洪水演进过程产生影响，因此，全场模拟是必要的。

还有一类具有健全物理基础的水沙动力学模型被应用于堰塞坝溃决的模拟，本文称为水沙动力学方法模型。水沙动力学模型将溃口形成与发展视为河床变形和水流之间的相互作用，同时采用土力学方法处理溃口因为重力失稳导致的坍塌。为反映堰塞坝坝体溃决过程中河床变形与水流之间的相互作用，王光谦等［23］针对唐家山堰塞坝特殊的漫顶泄流过程，在平面二维浅水方程的基础上增加了河床变形相关项，建立了平面二维水沙数学模型，较好地模拟了唐家山堰塞湖下泄流量与库内水位的变化过程，并分析了堰塞坝漫顶溃决过程中坝体的冲刷机制。同时，基于表面粗化层的非均匀沙输移过程来描述溃口段的沿程冲刷变化，建立了一维堰塞坝漫顶溃决数学模型［37-38］，并较好地模拟了唐家山堰塞坝漫顶溃决下泄洪水的变化过程。Cao等［39］以二维浅水水沙动力学方程为基本控制方程，运用修正的Meyer-Peter公式分析坝体的冲刷变化过程，建立了模拟天然坝漫顶溃决的二维水沙耦合数学模型，并对水槽试验进行了模拟验证且结果较好。Huang等［40］在此基础上，考虑天然坝体材料垂向分布不均匀的特征，采用简单几何方法处理侧向坍塌，构建了基于非均匀沙的二维水沙耦合数学模型，对唐家山堰塞坝漫顶溃决发展过程及下泄洪水变化过程进行了较好的复演。完整水沙耦合动力学模型不仅能够反映水沙运动过程，而且能够避免诸多土力学方法的假设。当然，这类模型也不可避免地引入经验关系，主要体现在泥沙输移公式、水流阻力计算方法上。需要指出的是这些经验关系在河流泥沙动力学中有长期经验积累，对其表现有较为清楚的认识［41］。目前能够对堰塞坝溃决全过程模拟的水沙耦合模型研究还较少，并且对于堰塞坝宽级配泥沙输移考虑得还不充分。因此，需要在现有的一维非均匀沙模型和二维均匀沙模型基础上，研发考虑宽级配非均匀泥沙输移、侧向侵蚀和重力坍塌溃口展宽机理的平面二维水沙耦合数学模型，并将堰塞湖库区淹没变化、堰塞坝溃决过程、下游洪水演进过程及其诱发的强烈泥沙输移和河床变形过程作为一个整体在模型中进行模拟。

3 下阶段研究展望

综上分析，作为自然作用的产物，堰塞坝几何形态、粒径级配和库容决定了其溃决机理的复杂性，而溃口演化的精细模拟和峰值流量的准确预测是应急处置的基础和关键。以往试验研究坝体尺度小（坝高0.3～0.8 m），缩尺效应不容忽视，试验坝坡较陡（坡比1∶2～1∶4），与实际堰塞坝体不相似；试验库容太小，坝前水位降落过快，导致溃口峰值流量和溃决过程与实际偏差较大；水槽试验坝体横向尺度较小，无法模拟最终溃口形态；等等。数学模型基于大量人为假设，物理机制不健全，均有待发展完善。

针对当前研究中存在的问题，下阶段拟从2个方面开展深化研究。一是开展大尺度模型试验研究，试验堰塞湖库容540 m3，坝体高1.5～2.0 m，坝体横河向宽4 m，可模拟溃口发展完整的物理全过程和最终溃口形态（以往水槽试验无法模拟或过程不相似）；二是开发能够模拟全场和溃决全过程的平面二维水沙耦合数学模型，考虑宽级配非均匀泥沙输移、侧向侵蚀和重力坍塌作用，摈弃长期以来的事先假设，因而溃决过程是水沙床耦合数学模型数值解的一部分，物理机制更健全。

3.1 大尺度模型试验研究

3.1.1 资料收集分析

充分收集调研国内外大中型堰塞湖基本参数，包括并不限于堰塞坝赋存特征与几何形态（坝高Hd、坝底顺流长Ld、坝宽Wd、下游坝坡坡比Sd、堰塞坝体积Vd）、物质组成与粒径级配、堰塞湖库容Vl与来流量Q0、溃决特征参数（如溃口峰值流量Qp、溃决历时Tb、最终溃口深度Hb、最终溃口底宽Wb、最终溃口顶宽Wt），见图3，分析各基本参数的相关性。特别是对于近年发生的致灾影响较大且资料收集较全的唐家山堰塞湖（图4（a））和金沙江白格堰塞湖（图4（b）），着重进行资料收集和溃坝洪水分析，为大尺度试验和数学模型研究奠定坚实基础。

图3 堰塞坝冲蚀典型纵横剖面Fig.3 Longitudinalprofileandcrosssectionof landslidedam erosio

图4 唐家山堰塞湖、金沙江白格堰塞湖冲蚀前后纵剖面Fig.4 Longitudinal profiles of Tangjiashan and Baige landslide lakes before and after erosion

3.1.2 试验方案设计

初拟大尺度试验布置全长50 m。其中上游水库长30 m，宽12 m，高1.5～2.0 m，试验库容540～720m3。水库内加设 2道可拆卸隔板，可研究不同库容对坝体冲蚀过程和峰值流量的影响。下游水槽长 20m，宽 4.0～6.0m，高 2.0～1.0m（见图 5）。试验进口控制入库流量Q0恒定，模拟坝高 1.0～2.0m，下游坝坡坡比 1∶2～1∶8。试验堰塞坝物质组成主要为直径 ＞0.005mm的无黏性土粒，粒径范围为 0.005～40mm。

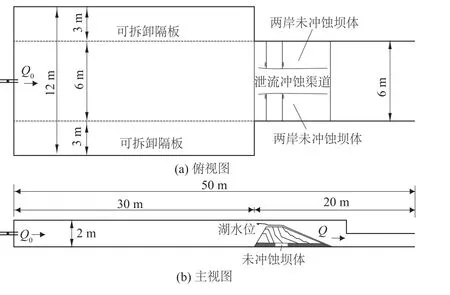
图5 堰塞坝溃决过程试验布置示意图Fig.5 Arrangements for landslide dam breaching test

试验特征值换算见表1。由表1可知，本试验方案设计可模拟原型堰塞坝最大坝高100～160 m，库容0.9亿～3.686 4亿m3，最大出库流量21 200～68 700 m3/s，河宽300～480 m；原型粒径范围0.25～3 200 mm，相当于粉粒、砂粒、砾粒、卵石、漂石甚至巨石等。基本可涵盖目前已收集到的绝大多数堰塞坝实际范围。应该指出的是，试验设计时应有效协调解决试验坝高、粒径级配、库容之间的匹配性和相似性。

表1 堰塞坝溃决试验特征值换算Table 1 Conversion of characteristic values of landslide dam breaching test

3.1.3 试验量测系统

鉴于溃口发展演变和溃口流量变化的强非恒定流特征，如何动态准确捕捉这一过程是试验成败的关键技术之一。①入库流量：在试验进口安装电磁流量计，量测控制入库流量；②库水位：在试验水库安装多支水位传感器，记录水位变化过程线，并实时监测水库库容变化；③溃口流量：由不同时刻库水位-库容曲线推求，注意区分溃口前缘和库区的水面梯度，并经均化处理；④溃口流速：采用布设在引冲槽部位的电磁流速仪或小威龙流速仪动态施测；⑤溃口形态：采用“埋入式轻型冲蚀捕捉器”动态记录，辅以网格和上下游固定点高清摄像技术，可实时记录溃口垂向冲蚀下切和横向扩展过程。与此同时，为准确进行水动力参数量测，可将坝体强非恒定流冲蚀过程概化为若干控制节点，将坝体冲刷动边界地形固化复演。在恒定流试验条件下，准确测试流速、流量、水深等参数。

3.1.4 研究重点

阐明堰塞坝破坏机制与溃口演变规律，揭示溃口发展物理全过程。对堰塞坝漫溢溃决全过程进行阶段划分，解析各阶段溃口控制断面形态和水流特点，揭示溃口演变和水流结构的互馈机制。分析溃口发展机理及力学特性，探索“陡坎”形成的条件及其对坝体几何形态、粒径级配和密实度的响应规律，揭示溃口峰值流量与宽顶堰流或明渠水流的相关性，论证坝高和下游坝坡坡度对溃决过程和峰值流量的作用机制。

3.2 水沙耦合全过程数值模拟

在现有的一维非均匀沙模型和二维均匀沙模型基础上，考虑宽级配非均匀泥沙输移、侧向侵蚀和重力坍塌作用，建立能够模拟全场和溃决全过程的平面二维水沙耦合数学模型。并将堰塞湖库区淹没变化、堰塞坝溃决过程、下游洪水演进过程及其诱发的强烈泥沙输移和河床变形过程作为一个整体在同一模型中进行模拟。摈弃长期以来对溃口流量、溃口形状、边坡坡度、残留坝体高程、溃决时间等的事先假设，使其成为水沙床耦合数学模型数值解的一部分，物理机制更健全。解决了溃决过程及其上下游水沙动力条件人为分段模拟的难题，同时将现有均匀沙模型扩展到非均匀沙模型，提高对溃决过程中泥沙颗粒分选过程模拟的能力。

建立在流体力学基本守恒律基础上的二维浅水水沙动力学控制方程，包括水流和泥沙的质量守恒方程和动量守恒方程。从物理上讲，该方程（式（1））能够适用于溃坝洪水、泥沙和河床变形过程的模拟。

其中：

式中：x、y为空间坐标；U为守恒量向量；F和G分别为x和y方向的对流通量向量；F～和G～分别为x和y方向的扩散通量向量；S为源项向量；t为时间；h为水深；u、v分别为x和y方向的水流流速；z为河床高程；ck为第k组泥沙的深度平均体积含沙量；C＝∑ck，为总含沙量；vt、εt分别为水流和泥沙的紊动扩散系数；g为重力加速度，取9.8 m/s2；Sfx、Sfy分别为在x和y方向的阻力坡度；Sbx、Sby分别为在x和y方向的河床坡度；p0为泥沙孔隙率；E＝∑Ek，为上扬通量总量；D＝∑Dk，为沉降通量总量；Ek、Dk分别为分组泥沙上扬通量和沉降通量；ρw和ρs分别为清水和泥沙的密度，分别取1.0×103kg/m3和2.65×103kg/m3；ρ为水沙混合体密度，ρ＝ρw（1-C）＋ρsC；ρ0为床沙饱和湿密度，ρ0＝ρwp0＋ρs（1-p0）。

河床变形由如下方程描述：

河床泥沙级配方程为

式中：δ为活动层厚度；fak为活动层分组泥沙的组分；η为活动层下界面位置，η＝z-δ；fsk为存储层上界面处的泥沙级配；N为级配组数。式（5）为非饱和模型框架下基于活动层模式的床沙分粒径组泥沙质量守恒方程，求解该方程可得到床沙组分级配随时间的演化。

模型中重力坍塌采用简单几何地形处理，即当计算边坡大于临界坡度时，将地形坡度人为修正为临界坡度，将水面以上的土体等面积地增加到河床上。泥沙上扬通量和沉降通量按照文献［39］中方法计算，其中饱和含沙量输移公式采用修正Meyer-Peter公式计算。阻力采用曼宁公式计算。模型数值格式采用Godunov型有限体积法，地形源项采用中分差分离散，阻力源项采用隐式格式离散［40］。

数学模型开发完成后，采用大尺度试验资料和实际堰塞湖溃决事件资料进行率定和验证，并对典型堰塞湖溃决事件进行复演，系统检验模型性能。

4 结 语

堰塞坝溃决过程与模拟技术是面向国家防灾减灾重大需求的前沿热点问题，在系统梳理国内外试验和数值模拟研究进展的基础上，提出了下阶段研究重点。大尺度模型试验研究重点是阐明堰塞坝破坏机制与溃口演变规律，揭示溃口发展物理全过程，填补以往小尺度水槽试验无法预演最终溃口形态以及库水位降落过快导致峰值流量不相似的不足，提升认知水平和预测精度。同时，开发全过程水沙耦合数学模型，摈弃长期以来对溃口流量、溃口形状、边坡坡度、残留坝体高程、溃决时间等的事先假设，而在水沙床耦合数学模型中这些事先假设是数值解的一部分，物理机制更为健全。研究成果对提高堰塞坝溃决洪水灾害防范的科学决策水平和应急处置能力具有重大现实意义。