瞬溃条件下不同溃决形式的溃口水力特性研究

郭红民，张 杨，柳 滔，杨百银，马 良，杨 莹

(1.三峡大学水利与环境学院，湖北宜昌443002；2.广西右江水利开发有限责任公司，广西南宁530000；3.水电水利规划设计总院，北京100120)

1 研究背景

混凝土坝由于材料强度较高且一致性较好，一般不易溃决，但在某些特殊条件下，如战争、地震、风暴潮、质量缺陷等，也可能发生溃决。大坝一旦溃决，巨大的水位落差，使水库中的蓄水经过溃口快速下泄到下游河道中，往往造成灾害性的突发洪水。

大坝不同的溃决方式及溃口形式对溃口的最大流量及相关水力特性影响很大，因此学者都较为重视，提出了许多溃坝溃决研究成果。如姚霄雯等[1]收集了国内外74座混凝土坝溃坝资料，总结了混凝土坝的溃坝特点，统计了主要溃坝原因，进而提出了坝基、坝肩破坏为混凝土坝最重要的溃坝模式；谢任之[2]系统的提出了可用于计算瞬时溃、逐渐溃、部分溃、全溃等情况的溃坝流量计算统一公式，并且还提出了适用于不同河道断面的溃坝流量过程线计算方法；曲霞[3]利用MIKE11模型对大凌河的溃堤洪水过程进行模拟分析，并选取实测洪水资料，对比模拟结果，表明能够较好地反映溃口洪水实际状况；姜治兵等[4]建立了坝体溃决过程与溃坝洪水演进耦合的平面二维数值模型，通过实际算例表明模型合理地模拟了溃口的发展与洪水演进过程；郭红民等[5]根据混凝土坝结构特征和受力特点，假定了3种可能的溃决方式，通过物理模型试验研究了3种溃决方式的溃口水力学特征，结果表明，3种溃决方式中滑动式溃口峰值流量最大，危害最大。

以往大部分溃坝研究主要讨论水库大坝的溃决流量过程或下游洪水的演进特征，而对于同一水库大坝考虑不同溃决形式下的溃口水力特性研究较少。本文基于混凝土坝瞬时溃决的基本假设，采用数值模拟计算的方法，以某一实际水库边界及混凝土坝为研究背景，比较研究了大坝横向局部溃决和垂向局部溃决下的溃口水力特性，为类似工程的大坝溃决及洪水传播研究提供参考。

2 模型构建

2.1 研究区域概况

某水电站为混凝土坝，坝高305 m，坝顶高程1 885 m，水库正常蓄水位1 880 m，总库容77.6亿m3。坝址处多年平均流量1 220 m3/s，多年平均年径流量385亿m3/s，本文的研究区域包括水库回水的干流河段及大坝下游的部分河段，模型中河道水深数据是根据实测断面资料经过插值加密处理后得到，断面间距为200 m，陆上地形高程来自ASTER GDEM V2[6]，并由当地河道水面高程进行了矫正处理，计算中在坝址上、下游各200 m处设置了水位观测点，用于观测库水位及下游河道水位的变化过程。

2.2 控制方程

本文构建的溃坝数值模型采用控制方程为

(1)

(2)

式中，Q为流量，m3/s；q为侧向入流，m3/s；A为过水面积，m2；h为水位，m；R为水力半径，m；C为谢才系数；α为动量修正系数。

2.3 计算初始条件

上游入库流量采用万年一遇洪水作为入流条件，由于该超标洪水过程的洪水历时较长，而在漫顶溃决条件下长时段的过程线对溃口峰值流量影响不大，故本文取最大3天洪峰的平均值作为来流洪水进行计算。

溃坝计算基于大坝漫顶时瞬时溃决，即大坝溃决时坝前水位为坝顶高程1 885 m；坝下起始水位为枢纽下泄上游来流量时的下游河道天然水位。

2.4 模型验证

由于所研究的大坝实际未发生过溃决，故模型的验证采用水库正常运行时段的水位特征进行。验证时段为某年7月～8月，验证结果如图1所示，计算值与实测值基本吻合，满足进一步研究的需要。

图1 水文站水位验证

3 计算工况

为研究混凝土坝瞬溃条件下不同溃决形式对溃口水力特性的影响，本文根据实际工程可能产生的溃决形式，将混凝土坝的溃决形式概括为横向局部溃决[7-9](在外力的作用下坝体发生结构破坏，导致部分坝段整体失稳或脱落)和垂向局部溃决[10-11](大坝溃决在某个高度发生，其下留有一定残高)。

为方便后期计算成果的比较，在设定横向局部溃决和垂向局部溃决的计算工况时，采用了溃口面积相等的溃口特征，即将大坝挡水横剖面面积A分别以横向、垂向局部溃决的溃口面积划分为1/4A、2/4A和3/4A两类共6种计算工况。图2、图3分别为横向局部溃决(工况1、2、3)、垂向局部溃决(工况4、5、6)的示意。

4 计算结果及分析

4.1 溃口流量

各溃决工况下溃口流量[12-14]过程线如图4所示，6种工况的溃口流量在溃坝发生后均在极短时间(约0.05～0.1 h)内达到最大流量。表1为等面积溃决溃口最大流量。

当横向溃决时，溃口最大流量随着溃口面积的增加而增加，但增速并不呈线性，当溃口面积较小时，增速较大，当溃口面积较大时，增速变缓；在库容相同情况下，溃口流量降速的快慢与溃口的大小、库容泄空的时间直接相关，如工况1溃口面积最小，库容泄空时间长，其溃口流量的下降速度就较缓，而工况2、3的溃口面积均较大，库容泄空时间较短，其溃口流量的下降速度均较快，下降过程差别不大。

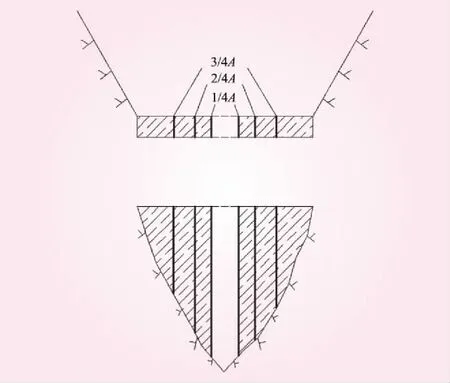
图2 横向局部溃决的3种工况

图3 垂向局部溃决的3种工况

图4 各工况下溃口流量过程

表1 等面积溃决溃口最大流量

垂向溃决由于存在残高底坎，使各工况下泄的库容不同，溃口流量总体仍随着溃口面积的增大而增大，且最大溃口流量的大小与残坎上的起始溃决水头高度有关。工况6时，由于溃口面积最大，起始水头也最大，溃口最大流量也最大。

由表1可知，当溃决面积相同时，横向溃决的最大溃口流量分别是垂向溃决的2.72、1.88和1.40倍，说明横向溃决的下降趋势比垂向溃决要快，水库泄空时间要短，这种差别主要是由于横向溃决的溃口部分是一溃到底，同面积条件下，溃口水头较高，溃口流量较大；而垂向溃决时，溃口留有一定残高，同面积溃决情况下，溃口水头相对较小，溃口流量也相对较小，流量下降也明显变缓。

4.2 流速

各工况溃口断面流速变化过程如图5所示，各溃决工况下溃口平均流速都是在溃决开始阶段快速增大，在极短的时间(约0.06 h)内达到最大值，然后再逐渐减小。表2为等面积溃决溃口最大平均流速。

图5 各工况下溃口处平均流速

表2 等面积溃决溃口最大平均流速

当横向溃决时，溃口最大流速随着溃口面积的增加而减小，但3种工况下溃口最大流速的差值并不大；在库容相同情况下，溃口流速下降的快慢与溃口面积、库容泄空时间有关，溃口面积较小时，泄空时间长，流速下降慢，溃口面积较大时，泄空时间短，流速下降快；如工况1溃口面积最小，库容泄空时间最长，其溃口流速的下降速度就较缓，而工况3的溃口面积最大，库容泄空时间最短，其溃口流速的下降速度也最快。

当垂向溃决时，溃口最大流速总体仍随着溃口面积的增大而增大，但3种工况下溃口最大流速的差别较大；垂向溃决由于存在残高底坎，使各工况的下泄库容不同，当残高底坎较高，下泄库容较小时，溃口最大流速也较小，下降趋势也更缓，残高底坎较低，下泄库容较大时，溃口最大流速也较大，下降趋势也更快，如工况6时由于溃口面积最大，残高底坎最低，下泄库容也最大，溃口最大流速也最大，下降速率也更快。

由表2可知，等面积溃决时，横向溃决的溃口最大流速分别是垂向溃决的2.69、1.78和1.30倍，横向溃决比垂向溃决具有更大的流速，且流速变化更剧烈，这是因为同面积条件下，横向溃决库容泄空时间短，溃口水头较高，溃口流速大。

4.3 水位

混凝土坝在各溃决工况时，上、下游水位测站处的水位变化情况如图6、7所示，水位变化过程直接与水库库容及溃口流量变化过程相关。

图6 上游水位变化

图7 下游水位变化

坝体一旦溃决，上游库区水位即快速下降，下降速率以工况3最大，工况4最小。当横向溃决时，随着溃口面积的增加，水库放空时间较快，水位下降则越快，趋于稳定的耗时越短，由于溃决后的底部高程相同，溃决后3种工况的稳定水位相同；当垂向溃决时，3种计算工况(4、5、6)中，随着溃口面积的增加，水库溃决水头也相应增加，水位的降速也相应增加，但最后水位趋于稳定的耗时大致相同。溃决面积相同时，横向溃决比垂向溃决水位的下降速率一般更快。

溃坝下游水位变化，工况1～6的水位上涨时间大致都在约0.1 h时达到最大，下游水位上升最高的峰值是工况3，最小的是工况4，水位达到峰值后均逐渐下降，之后趋于平稳。横向溃决时，随着溃口面积的增加，溃口最大流量增加，水库放空时间较快，水位变化呈“尖”“陡”的特点，趋于平衡的耗时较短；垂向溃决时，由于水库放空时间相对较慢，水位的变化总体呈现快速上升缓慢下降的形态，趋于平衡的耗时越长。

5 结 论

(1)混凝土坝横向溃决和垂向溃决的溃口流量都是随着溃口面积的增加而增大，而横向溃决的总体溃口流量较大，下降较快，泄空时间较短，垂向溃决的总体下降趋势比横向溃决要缓；等面积溃决时，随着溃口面积的增大，横向溃决的最大流量分别是垂向溃决的2.72、1.88和1.40倍，即等面积溃决时横向溃决比垂向溃决具有更大的危害，溃口面积越小，差别越明显。

(2)横向溃决由于溃口水头大，溃口处平均流速整体较大，泄空时间随着溃口面积的增大而缩短，流速下降也越快；垂向溃决的溃口水头相对较小，流速相对较小，下降相对较慢；等面积溃决时，横向溃决比垂向溃决具有更大的流速，且流速下降变化更剧烈。

(3)横向溃决随着溃口面积的增加，水库放空时间加快，上、下游的水位变化也越快，趋于稳定的耗时越短；垂向溃决随着溃口面积的增加，水库水位的下降速率也增加，但水库的放空时间差别不大，下游水位在快速上升后，其下降过程均相对较缓慢，而趋于稳定的耗时则大致相同。