非黏性堤防溃口发展过程计算模型
2024-02-21段文刚
段文刚,刘 备,黄 卫
(长江科学院 水力学研究所,武汉 430010)
0 引 言
堤防作为防洪工程的重要组成部分,在世界各国内被广泛应用,对社会经济发展起到了重要作用。但在超标准洪水等情境下,由漫溢引起堤防溃决的案例时有发生[1],溃决洪水会对洪水淹没区人民的生命财产造成严重危害。堤防溃决过程是堤防材料与溃口水流相互作用的过程,量化分析溃口发展速率和水力要素的关系,构建溃口发展过程计算模型对于溃决过程模拟、下游洪水发展预测、人员紧急疏散预案的制定具有重要意义。现阶段在堤防溃口发展过程方面,相关研究成果主要集中在堤防溃口发展过程影响因素研究和溃口发展过程计算模型研究方面。
影响堤防溃口发展过程的因素主要分为两类[2]:一类是影响堤防抗冲力的因素,如颗粒粒径、堤防材料、堤防形态[3]、固结作用、压实度、含水率等;另一类是影响水流冲刷力的因素,如入流流量、河道水位等。Tabrizi等[4-5]通过水槽试验,研究了不同流量条件下堤防的溃决过程,发现溃口处的流速越大,溃口的展宽速率越快,还研究了压实度对堤防表面轮廓变化的影响,并建立了堤顶高度和堤底长度随堤料干密度变化的无因次方程;Zhu等[6]在试验中观察到黏性堤防溃决存在溯源“陡坎”冲刷现象,而非黏性沙质堤防溃决并未出现“陡坎”现象,并且黏性土能够很大程度地减缓堤防溃决冲刷速度;魏红艳等[7-8]通过开展水槽试验,发现筑堤土体含水率与孔隙率不仅影响了溃口垂向下切和横向展宽速率,而且决定了溃口最终形态,入流流量主要影响堤防溃口的横向展宽速率;梁艳洁等[9-10]发现河道流量越大,溃口最终宽度也越大,溃决初始洪水位越高,溃口展宽速度也越快,粗颗粒材料堤防在溃决初期溃口展宽速度略大于细颗粒材料堤防,后期变化趋势相反;果鹏等[11]通过溃决试验得到溃口展宽速率与入流流量呈正相关关系的规律。
在堤防溃口发展过程计算模拟方面,现应用较为广泛的模型主要有两类:基于数据统计的参数模型和基于物理机制的数学模型。基于数据统计的参数模型,主要利用一些关键的溃口几何及物理参数,通过较简单的时变过程来模拟溃口的发展过程,对历史溃堤资料运用统计学方法进行回归分析[12],建立得到溃口展宽、溃口下切等参数的经验公式,这些公式结构相对简单,可以对溃口发展过程进行快速评估。但是,经验公式的建立通常需要大量的实测数据为基础,由于溃堤的危险性和复杂性,收集到的资料极为有限,数据的精度也较差,因此经验公式具有一定的局限性,且此类模型并未涉及到实际的溃决机理,准确度较低,计算结果不稳定[13]。基于物理机制的数学模型,主要运用水力学和泥沙动力学等方法,采用微分方程描述溃口发展和侵蚀过程,能够较为真实地模拟实际溃堤过程,如陈珺等[14]在Zhang等[15]已建立的平面二维非恒定、非均匀沙不平衡悬移质泥沙数学模型的基础上,考虑了溃口横向展宽及坍塌、垂向冲刷,借鉴Darby等[16]提出的分析黏性土河岸稳定性的方法,建立了一种能够模拟堤防溃口展宽和冲深的数学模型。但此方法求解复杂且计算中大多含有某些不易现场测量的参数,这些都限制了方程的建立与普遍适用性[17]。且多数基于物理机制的模型存在一些与实际情况明显不符的假设,如假设溃口横向和垂向冲刷为均匀冲刷,或者泥沙冲蚀速率与溃口水深仅存在简单的函数关系,这些假设会导致计算结果可靠性不高。
综上所述,有关溃口发展速率方面的研究相对较少,且仅有的这些研究均是定性分析,并未给出溃口发展速率的决定因素以及它们之间的量化关系表达式。本文采用系列堤防溃决物理试验的高精度地形和流量过程资料,量化分析了溃口发展速率与溃口流量、溃口单宽流量之间的关系,构建了以溃口单宽流量为参数的溃口发展过程计算模型,并对溃口垂向下切、横向展宽发展过程进行了模拟计算与对比分析,结果显示模拟情况与真实的溃口发展过程吻合较好,证明了该计算模型具有较高的精度和科学性,且计算过程简洁,为堤防险情处置提供科技支撑。
1 研究方法
1.1 试验系统简介
该试验系统[18]由河道、可冲刷的侧向堤防、不可冲刷底板以及蓄滞洪区组成(见图1(a))。主河道长10 m,宽1 m,可冲刷侧向堤防与来流方向平行,不可冲刷底板4.3 m×2.5 m。在大多数试验中,通过堤防溃口的水流可自由地从洪泛区排出,不会影响溃口水流。在所有试验中,堤防修筑均采用非黏性均匀沙质材料,即中值粒径d50=1 mm的均匀粗沙,堤长均为3 m,堤高0.3 m,堤顶宽度W=0.1 m,内外堤坡度为1∶2,堤底宽度1.3 m(见图1(b))。为了保证漫顶溃决发生部位相同,模型在堤顶距上游端0.85 m处开挖了一个深H0=0.02 m、宽B0=0.1 m的矩形初始缺口。

图1 漫溢溃堤试验平面布置Fig.1 Plane layout of experiment for embankment breaching
本试验采用激光轮廓测量技术(Laser Profile Measurement Technology,LPT),监测堤防溃决过程,这是一种非接触式测量方法,能够避免测量过程对试验结果造成影响,得到堤防的实时地形数据。水位测量系统:在主河道、不可冲刷底板共布置5个水位计(见图1),用来测量主河道等位置的水位。流量测量系统:采用电磁流量计测量入流流量,在河道下游布置溢流堰测量河道出流量,溃口流量通过河道水位库容曲线与水量平衡计算得出。通过多组工况的分析发现,溃口流量过程符合侧堰溢流规律,溃口发展过程也和已有的试验结果相一致,试验观测数据具有较高的可靠性。试验中控制其他条件不变,改变上游入流流量,共计4组试验工况(见表1)。

表1 试验工况汇总Table l Summary of experimental conditions
试验中流入主河道的流量保持恒定。以堤防的初始缺口刚刚发生漫溢为0时刻,开始记录堤防的地形变化及主河道、不可冲刷底板的水位过程。
1.2 数据处理
选取堤顶宽度方向中部(y=0.65 m)横截面所在平面为研究区域,该截面尺寸为3.0 m×0.3 m,堤防地形数据为沿着所选截面x方向间隔0.01 m分布的测点高程值z。首先确定各组试验的溃口位置,在计算地形差异时,只需要溃口位置的测点数据,其他区域的结果可能就是测量误差。每组试验选取多个时刻T,不同时刻地形差可以用z的差值进行计算,根据所选时刻Ti与上一时刻Ti-1溃口位置下切深度最大的中间部分区域测点的高程变化平均值dz,计算得到所选截面溃口Ti时刻的下切速率Vz=dz/dT,这样可以有效消除上游来沙和溃口边缘坍塌所造成的影响,取Vz滑动平均值可以有效避免因为测量方法等造成的测量误差和偶然误差,得到的关系曲线更加光滑,更具有合理性。在计算所选时刻的溃口展宽速率时,溃口宽度采用溃口水面宽度,读取高程值小于溃口水位的测点个数S,S×0.01即为该时刻的溃口宽度,根据所选时刻Ti与上一时刻Ti-1的溃口宽度差值db,计算得到溃口Ti时刻的展宽速率Vb=db/dT。
2 溃口发展分析
2.1 溃口流量过程
4组试验工况的河道水位变化和溃口流量过程曲线如图2所示。工况1,入流流量0.020 m3/s,溃口峰值流量为0.030 m3/s,峰值时间为第48 s,最终溃口流量趋于稳定值0.020 m3/s;工况2,入流流量0.030 m3/s,溃口峰值流量为0.030 m3/s,峰值时间为第65秒,最终溃口流量趋于稳定值0.030 m3/s;工况3,入流流量0.040 m3/s,溃口流量迅速增长后转入缓慢增长,最终溃口流量趋于稳定值0.038 m3/s;工况4,入流流量0.055 m3/s,溃口流量迅速增长后转入缓慢增长,最终溃口流量趋于稳定值0.047 m3/s。可以看出在入流流量较小时(工况1、工况2),溃口流量迅速增大,到达峰值后缓慢减小,最后趋于稳定,溃口流量经历了增长、回落、稳定这3个阶段;在入流流量较大时(工况3、工况4),溃口流量总体呈现快速增长、缓慢增长直至稳定3个阶段;河道水位都经历了缓慢增长后进入迅速下降并逐渐趋于稳定。这是因为水流在水位较高时主要通过溢流堰出流,随着溃口宽度、深度逐渐增大,溃口泄流量迅速增大,但河道调蓄能力有限,在经历大流量泄流后,河道水位快速下降,水流主要通过堤防溃口出流,最终溃口流量均趋向于入流流量,溃口流量过程符合堤防溢流规律。
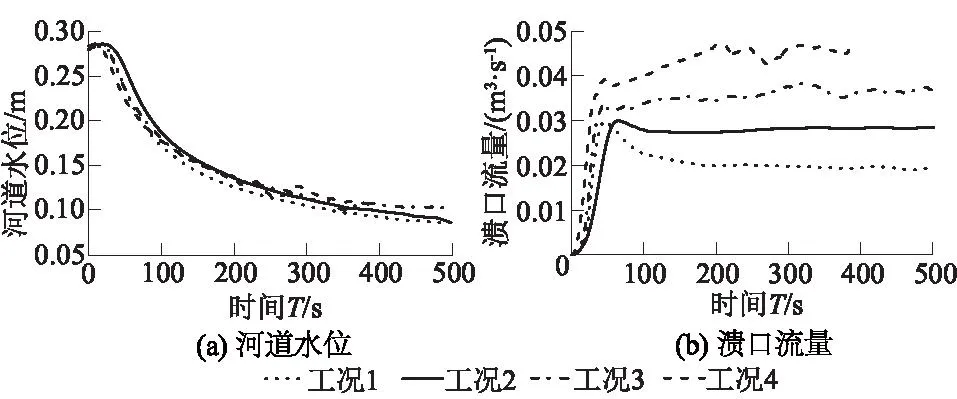
图2 河道水位与溃口流量过程曲线Fig.2 Curves of river water level and discharge at the breach with time
2.2 溃口形态发展过程
从试验和现场观测资料中总结发现,溃口发展主要是水流冲刷土体所造成的,并伴随边坡间歇性失稳坍塌现象,溃口的横向宽度和垂向深度在过流水流作用下逐渐增大,非黏性沙质堤防的溃口形态大多近似于梯形。如图3所示,梯形IJKL为初始溃口形态,梯形MNOP为新的溃口形态,溃口宽度增加Δb1+Δb2,溃口深度增加Δz。

图3 堤防溃口形态概化Fig.3 Generalized form of embankment breach
分析发现各组试验中溃口形态特征相似,以工况1为例,绘制了不同时刻堤防溃决过程三维地形(图4)和局部溃口形态发展过程剖面(图5)(y=0.65 m)。
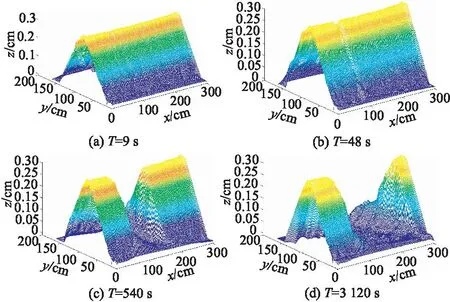
图4 堤防溃决过程Fig.4 Process of embankment breaching

图5 溃口形态发展过程Fig.5 Development process of breach
通过分析试验过程发现,依据溃决特征可将整个溃决过程划分4个阶段:沿程冲刷阶段、溯源冲刷阶段、快速发展阶段、发展稳定阶段。第1阶段为沿程冲刷阶段,水流从导流槽流出后在下游坡面沿程冲刷,坡面呈现“辫状”河道的特征(见图4(a)),溃口处过流能力、水动力较弱,流速流量较小,溃口扩展不明显;第2阶段为溯源冲刷阶段(见图4(b)),溯源冲刷从下游往上游发展,坡面水沟两侧土体坍塌,堤顶导流槽尺寸变化较小,随着冲刷进行,当溯源冲刷到达上游坡面时,溃口开始展宽,开始进入快速发展阶段;第3阶段为快速发展阶段(见图4(c)),溃口横向展宽、垂向下切的发生主要集中在此阶段,溃口宽度、深度迅速增大,过流能力逐渐增强,溃口流量迅速增长到达峰值,溃口垂向下切到达堤防底部后,溃口发展后续主要以横向展宽为主;第4阶段为发展稳定阶段(见图4(d)),溃口展宽过程基本结束,河床仍在缓慢冲刷,溃口最终形状表现为梯形。不同入流流量工况试验中均发现:堤防溃决过程中,溃口垂向冲刷率先完成,溃口形态暂呈现U形,随着溃口横向扩展,溃口宽度逐渐增大,最终形成梯形溃口(见图5),4组工况最终的溃口宽度分别为1.9、2.1、2.1、2.2 m。
3 溃口发展速率与水力要素关系分析
Tinney等[19]、Visser[20]和Coleman等[21]在研究堤防溃决溃口发展时,借鉴土力学的方法,用水流剪切应力、土体起动剪切应力和侵蚀系数表示土体冲刷宽度(速率),建立以剪切应力为变量的溃口发展过程参数表达式,即
E=kdΔt(τ-τc)或Vz=kdt(τ-τc) 。
(1)
式中:E为冲刷宽度(m);kd为侵蚀系数;Δt为时间(s);τ为水流平均剪切应力(Pa);τc为土体起动剪切应力(Pa);Vz为溃口下切速率(m/s)。
只有当水流剪切应力大于土体剪切应力时,土体才会被水流冲走。从式(1)可以看出土体冲刷速率除了受水流作用力影响外,还与土体的侵蚀系数和起动剪切应力有关,而侵蚀系数和临界剪切应力均与土体本身性质有关,其中侵蚀系数是决定土体冲刷速率最主要的参数,针对不同土体的临界剪切应力有众多经验公式可以计算,并且两者具有一定的关系。求解水流剪切应力时受水深影响较大,而由于溃口处高程变化剧烈,其溃口底高程很难测得,因此无法准确求出水深,溃决初始时,水深很小,水沙界面更难以辨别,也为水深的确定增加了困难。此外1934年Schoklitsch[22]也指出在确定具有陡坡天然河流中的泥沙起动规律时,使用水深(剪切应力)作为变量不适用,并尝试研究用流量确定推移质,通过分析引入单宽流量作为变量建立了推移质计算公式,即
gb=2 500S3/2(q-qc) 。
(2)
其中,
式中:gb为单位时间内单位宽度上推移质输移的质量(kg/(s·m));S为河床坡度;q为单宽流量(m2/s);qc为泥沙开始起动的临界单宽流量(m2/s);γ、γs分别为水流、泥沙重度(kN/m3);d为泥沙粒径(m)。
Julien等[23]和Govers等[24]分别建立了以溃口单宽流量为变量的水流挟沙力Tc计算公式,即
Tc=AS1.31q1.93,Tc=AqBSC。
(3)
式中A、B、C均为参数。因此推测以溃口单宽流量为特征参数的溃口发展速率公式更具有合理性。
3.1 溃口发展速率与溃口流量的关系
通过前面分析,发现溃口流量与溃口形态相互影响,结合已有的研究成果,可知溃口发展速率与溃口流量密切相关。Campbell等[25]发现在天然多沙河道中,水流流量较小时流量与输沙率常成如下指数关系,即
Gs=AQn。
(4)
式中:Gs为单位时间内泥沙输移总量(kg/s);A为与泥沙特征、河床坡度等相关的系数;Q为水流流量(m3/s);n是指数。
因此对溃口下切速率、展宽速率与溃口流量的关系进行了探索。通过对试验数据的整理,获得溃口流量Q与溃口下切速率Vz、溃口展宽速率Vb的关系如图6所示。

图6 溃口发展速率与溃口流量的关系(工况1)Fig.6 Relationship between development rate and discharge of the breach in working condition 1
从图6可以看出,溃口流量较小时,溃口下切速率Vz、展宽速率Vb较小,这是因为在溃口发展阶段,溃口水流流速较小,冲刷能力较弱。分析整理中也发现Vz存在负值,其绝对值较小,表明溃口发生了淤积,这种现象主要短暂出现在沿程冲刷阶段。出现此情况主要有两方面的原因:一是在此阶段水流冲刷溃口挟带泥沙堆积在溃口下游区域;二是由于溃口边坡土体在重力与水动力的作用下坍塌滑落进入了溃口的底部。
当入流流量较小时(0.02 m3/s),溃口下切速率与溃口流量分阶段近似呈线性正相关。在溃口流量增长阶段,溃口下切速率随着溃口流量增大而增大,下切速率达到峰值时,流量仍在增加,下切速率达到最大0.002 2 m/s,溃口流量Q达到0.026 m3/s,当溃口流量继续增大至峰值0.030 m3/s,相应下切速率减小至0.001 7m/s;在流量回落阶段,溃口下切速率与溃口流量缓慢减小直到趋于稳定值。流量增长阶段溃口下切速率与溃口流量的关系式为
Vz=0.080 1Q-0.000 2,R2=0.899 5 。
(5)
流量回落阶段溃口下切速率与溃口流量的关系式为
Vz=0.065 5Q-0.001 1,R2=0.748 3 。
(6)
溃口展宽速率与溃口流量的关系大致分为2个阶段:流量增长阶段,两者呈现二次抛物线关系,溃口展宽速率达到峰值时,溃口流量仍在增加,展宽速率达到最大0.023 9 m/s,溃口流量达到0.019 m3/s,当溃口流量继续增大至峰值0.030 m3/s,相应下切速率减小至0.015 6 m/s;流量回落阶段,两者呈现线性正相关,随着溃口流量逐渐减小并趋于稳定值,溃口的展宽速率也逐渐减小趋于稳定值。流量增长阶段溃口展宽速率与溃口流量的关系式为
Vb=-72.271Q2+2.674 4Q-0.000 8,
R2=0.981 1 。
(7)
流量回落阶段溃口展宽速率与溃口流量的关系式为
Vb=0.546 9Q-0.010 3,R2=0.663 2 。
(8)
经过试验数据回归分析发现,在堤防溃决过程中溃口流量和泥沙的冲刷速率呈现类似上述的指数关系,但也发现堤防冲刷和河道冲刷存在一些不同。堤防溃决时溃口流量相同的情况下,不同阶段的溃口发展速率也会有所不同,流量增长阶段的溃口发展速率明显大于流量回落阶段的,无法找到可以表达堤防溃决全过程统一的量化关系式。这是因为河道冲刷主要表现为河床底部的泥沙输移,而河道宽度基本不会发生变化,即过水断面的宽度不变,流量不变时单宽流量不发生变化;而堤防溃决冲刷过程中,堤防溃口发展存在2种形式(横向展宽与垂向扩展),随着溃决过程进行,溃口宽度逐渐增大,流量回落阶段溃口尺寸较大,溃口断面流速降低,溃口下切、展宽速率也相对较小。
同时多工况试验结果还表明在上游入流流量较小时,溃口发展速率与溃口流量存在上述明显的阶段规律。但是,在上游入流流量较大时,没有明显的流量回落阶段,上述规律失效。以工况4为例,入流流量较大时(0.055 m3/s),在溃决全过程中,溃口发展速率与溃口流量无明显定量关系(图7),与工况1中的阶段规律不同。

图7 溃口发展速率与溃口流量的关系(工况4)Fig.7 Relationship between development rate and discharge of the breach in working condition 4
3.2 溃口发展速率与溃口单宽流量的关系
上述以溃口流量Q为主要变量建立了其与溃口下切速率、展宽速率的关系。从结果可以看出,在不同溃决发展阶段溃口发展速率与溃口流量表达式的形式和参数均不同,不同入流流量下溃口发展速率与溃口流量关系的规律也不一样,因此存在着一定不足。为了建立适用于整个溃决过程且适用于各种工况的溃口发展参数表达式,本节进一步提出以溃口单宽流量q为变量,建立其与溃口下切速率、展宽速率的关系。
如图8所示,溃口发展速率与溃口单宽流量总体呈现指数关系,经过进一步数据处理分析,发现堤防溃口冲刷存在临界单宽流量,经过试验率定其值为0.01 m2/s。在溃决前期沿程冲刷阶段和溃决后期发展稳定阶段,溃口单宽流量小于临界值,溃口水流冲刷作用弱,展宽速率和下切速率均为0 m/s,溃口大小不变,这与实际溃决过程一致;当溃口单宽流量大于初始临界值0.01 m2/s时,溃口处的粗沙在水流作用下运动,溃口横向宽度和垂向深度增大,溃口发展速率与溃口单宽流量呈指数关系。溃口下切、展宽速率随着溃口单宽流量增大而增大,且增长速度逐渐增大,经过曲线拟合可得入流流量在0.020、0.030、0.040、0.055 m3/s时溃口下切、展宽速率与溃口单宽流量的定量关系(图8)。

图8 各工况溃口发展速率与溃口单宽流量的关系Fig.8 Relationship between development rate and unit-width discharge of the breach in each working condition
对工况1、3、4的试验数据进行拟合,得到多工况下的溃口发展速率公式,将其与各单工况下的结果进行对比,探究所得规律公式的适用性。
从图9可以看出多工况下溃口下切、展宽速率与溃口单宽流量的关系均为指数关系,与单工况拟合得到的函数关系形式完全一致,其函数表达式的形式均为:Vc=αeβ(q-qc)(α、β均为待定系数,qc为溃口单宽流量临界值),其中溃口下切速率与溃口单宽流量表达式为:Vz=αzeβz(q-qc),溃口展宽速率与溃口单宽流量表达式为:Vb=αbeβb(q-qc),可见溃口发展速率与溃口单宽流量之间的指数关系与泥沙冲蚀输移规律一致。

图9 多工况溃口发展速率与溃口单宽流量关系Fig.9 Relationship between development rate and unit-width discharge of the breach in various working conditions
由上可得以下规律:溃口发展速率与溃口单宽流量呈指数关系,此种关系形式在小流量条件下不受入流流量的影响;对比同一个工况试验中,相同时刻的溃口展宽速率明显大于下切速率,进一步分析可以发现在溃口快速发展阶段,溃口单宽流量相同情况下,溃口展宽速率约为下切速率的8~10倍。
表2展现的是4种入流流量不同的试验工况下溃口下切速率、展宽速率与溃口单宽流量指数函数表达式中的待定系数,从结果来看,溃口发展速率与溃口单宽流量密切相关,两者的关系形式为指数关系,且适用于溃决全过程及各种入流流量试验工况,但函数表达式中的待定系数具体数值受到入流流量的影响。
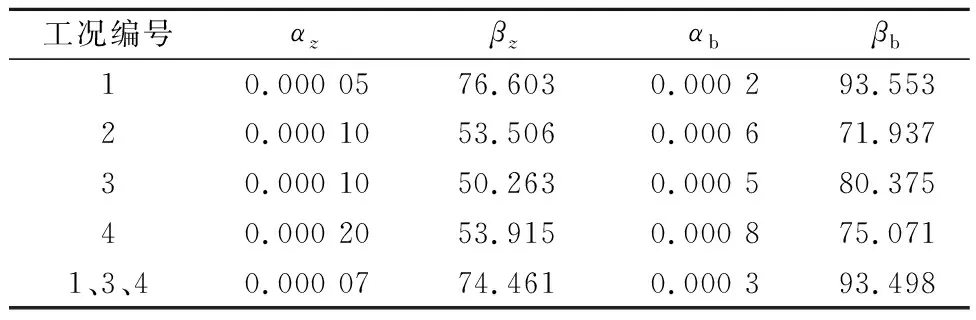
表2 溃口下切速率、展宽速率与溃口单宽流量函数表达式中的待定系数Table 2 Undetermined coefficients in the function expres-sions of the relationship between development rates (tran-sverse widening rate and vertical down-cutting rate) and unit-width discharge of the breach
3.3 溃口发展速率公式验证
利用工况1、工况3、工况4的试验数据拟合得到的溃口发展速率公式对工况2的溃口发展过程进行计算分析,验证溃口发展速率公式的可靠性。基于以单宽流量为变量的溃口发展速率公式,构建溃口发展过程计算模型,溃口发展过程计算如下。
溃口宽度变化公式为
B=B0+ΔB(q)Δt;
(9)
溃口深度变化公式为
H=H0+ΔH(q)Δt;
(10)
溃口冲刷速率综合公式为:
ΔB(q)=Vb=αbeβb(q-qc);
(11)
ΔH(q)=Vz=αzeβz(q-qc)。
(12)
将式(3)代入式(1)得
B=B0+αbeβb(q-qc)。
(13)
将式(5)代入式(2)得
H=H0+αzeβz(q-qc)Δt。
(14)
以工况2为例,此处B0=0.1 m,H0=0.02 m,qc=0.01 m2/s,αb=0.000 3,βb=93.498,αz=0.000 07,βz=74.461。由式(13)、式(14)计算得到工况2溃口横向宽度与垂向深度变化过程如图10(a)、图10(b)所示,溃口横向展宽速率与垂向下切速率变化过程如图10(c)、图10(d)所示。

图10 计算与实测溃口地形过程对比Fig.10 Comparison of breach topography between calculation and measurement
从图10可以看出,利用上述拟合的溃口冲刷速率与溃口单宽流量的综合公式计算得到的溃口地形与实测地形数据吻合度很高,溃口横向展宽和垂向下切速率模拟结果和实测值趋势一致,吻合度较高。参考《水文预报规范中洪水预报》(GB/T 22482—2008)中精度评定标准,用确定性系数DC来表示计算过程与实测过程之间的符合程度,0≤DC≤1,DC越趋近于1说明计算过程与实测过程符合度程度越好。其计算公式为
(15)
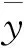
溃口宽度计算值与实测值确定性系数DC=0.920,溃口深度计算值与实测值确定性系数DC=0.986,由此可见根据溃口发展速率综合公式计算的溃口地形发展过程与试验中的溃口发展过程符合程度较好,计算模型具有较高的精度和科学性,且计算过程简洁。
需要指出的是,由于本文公式相关系数回归分析所采用的试验数据的流量范围(0.020~0.055 m3/s)有限,堤防材料特征都较为单一,对于超过本文试验条件的情况下,相关系数可能需要重新率定。同时泥沙侵蚀与溃口发展是一个复杂的现象,在不同条件下影响溃口展宽速率的关键因子有所不同,可能也存在其他形式的溃口展宽速率公式。
4 结 论
本文分析揭示了溃口流量、溃口单宽流量对于溃口发展速率的影响规律,建立了以溃口单宽流量为特征参数的溃口发展速率表达式,相关结论如下:
(1)溃口发展速率与溃口流量有关,整体呈正相关关系,但两者的关系受入流流量的影响,无统一的量化关系式。相同溃口流量下,流量增长阶段的溃口发展速率大于流量回落阶段的溃口发展速率。
(2)相同溃口单宽流量下,溃口的展宽速率大于下切速率。对于堤防溃决,横向破坏是溃决的主要形式。溃口的发展速率与溃口的单宽流量密切相关,溃口展宽速率、下切速率均与溃口单宽流量呈现指数关系,且此关系不受入流流量的影响。
(3)基于试验数据率定的溃口发展速率与溃口单宽流量指数关系,提出的堤防溃口发展过程计算模型,较好地复演了堤防展宽和下切过程,证明了本文提出的以溃口单宽流量为变量的溃口发展速率表达式结构合理,基于此关系构建的溃口发展过程计算模型具有较高的精度。
