传递函数辨识(18):输出误差模型的辅助模型递阶迭代参数估计

丁 锋,刘喜梅

(1.江南大学 物联网工程学院,江苏 无锡214122;2.青岛科技大学 自动化与电子工程学院,山东 青岛266061)

辅助模型辨识思想能够解决存在不可测变量系统的辨识问题,多新息辨识理论能够提高辨识算法的精度,递阶辨识原理可以解决大系统辨识方法计算量的问题,滤波辨识理念能够解决有色噪声系统辨识问题等。在连载论文中,使用这些思想、理论、原理、理念[1-6],先后研究了信号模型的参数估计,基于脉冲响应和阶跃响应的传递函数参数估计,以及基于正弦响应和频率响应的传递函数参数估计问题[7-12]。不同于先前辨识连续系统传递函数参数,本文研究离散时间传递函数描述的输出误差模型的统计辨识方法。利用系统的输入输出数据,提出了辨识传递函数模型参数的迭代估计方法,包括辅助模型(多新息)梯度迭代算法、辅助模型(多新息)最小二乘迭代算法、辅助模型递阶(多新息)梯度迭代算法、辅助模型递阶(多新息)最小二乘迭代算法。本文提出的递阶迭代辨识方法可以推广用于其他线性和非线性系统的参数辨识[13-21]。

1 输出误差系统的辨识模型

考虑下列输出误差模型(output-error model,OE模型)描述的输出误差系统:

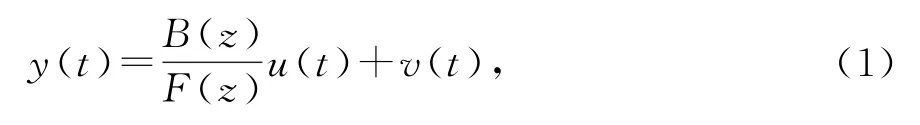
其中u(t)和y(t)分别是系统的可测输入输出,v(t)是零均值、方差为σ2的白噪声序列,B(z)和F(z)是单位后移算子z－1的多项式:

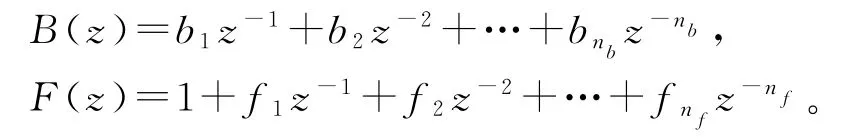
设阶次n f和n b已知,记n＝n f＋n b,且t≤0时,y(t)＝0,u(t)＝0,v(t)＝0。

定义系统未知真实输出:

y(t)为x(t)的含噪量测。定义参数向量ϑ和信息向量φ(t)如下:

由式(2)可得

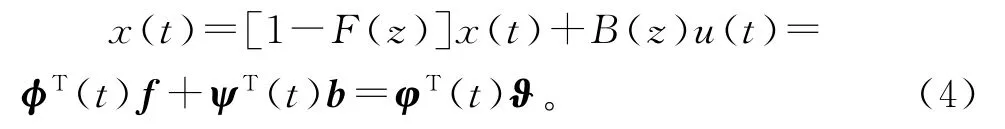
将式(2)代入式(1),使用式(4),可得

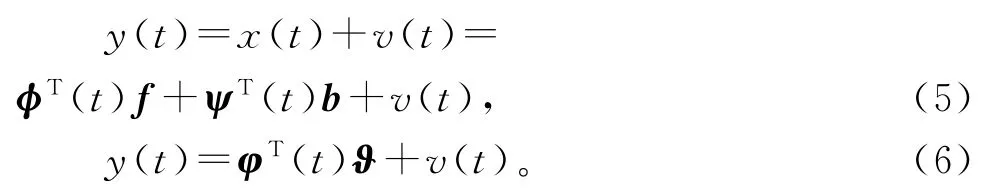
这就是输出误差系统的辨识模型。信息向量φ(t)包含了系统的可测输入数据u(t－i)和未知无噪输出变量x(t－i),参数向量ϑ包含了系统的所有参数f i和b i。

2 辅助模型梯度迭代辨识算法

辨识模型(6)中信息向量φ(t)是未知的,因为其除了包含系统可测输入数据u(t－i),还包含了未知无噪输出变量x(t－i),这是输出误差系统辨识的困难。解决这一困难的方案是使用辅助模型辨识思想[2,4],用系统的可测信息(包括计算获得的信息)建立一个辅助模型,用辅助模型的输出代替这些未知变量,从而获得基于辅助模型的辨识方法。具体思路如下。

用ψ(t)、φ(t)的估计构造φ(t)的估计:

根据式(4),用φ(t)的估计和参数估计构造估算x(t)的辅助模型:

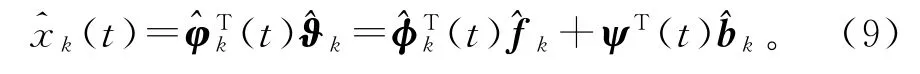
可作x(t)在时刻t的第k次迭代估计。

设L为数据长度。迭代算法的参数估计精度取决于数据长度,因此数据长度应足够大。考虑输入输出{u(t),y(t):t＝1,2,…,L},定义堆积输出向量Y(L)和堆积信息矩阵Φ(L)如下:

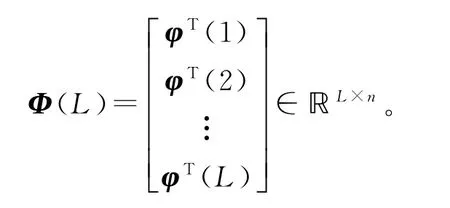
根据辨识模型(6),定义静态数据窗准则函数:

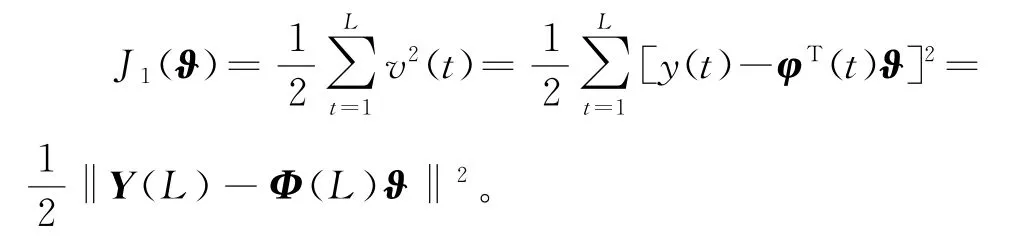
令μk≥0为迭代步长,即收敛因子。使用负梯度搜索,极小化准则函数J1(ϑ),得到关于的梯度迭代关系:

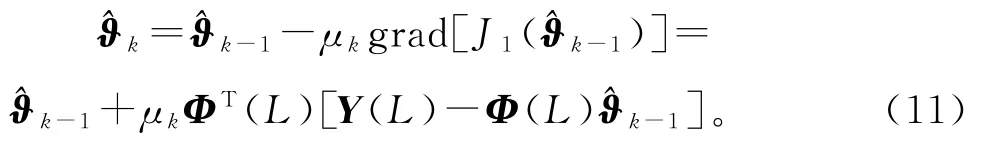
由于φ(t)(t＝1,2,…,L)中包含了未知中间变量x(t－i),由φ(t)构成的堆积信息矩阵Φ(L)是未知的,所以式(11)无法计算出迭代参数估计^ϑk。为了解决这个问题,这里采用辅助模型辨识思想,用式(8)中φ(t)的迭代估计(t)构造堆积信息矩阵Φ(L)的估计:

用(L)代替式(11)中的Φ(L),得到

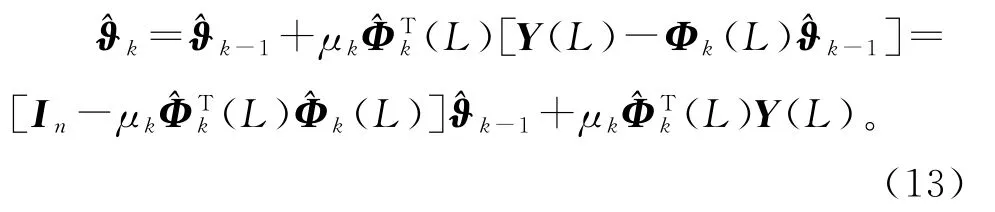
式(13)可以看作状态为的离散时间系统,为保证收敛,矩阵的所有特征值必须在单位圆内,因此μk的一个保守选择是满足

其中λmax[X]为矩阵X的最大特征值。为避免特征值的计算,步长可简单取为

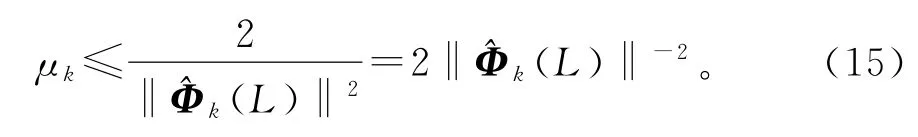
式(13)～(15),(10),(12),(8),(7),(3)和(9),构成了辨识输出误差系统(1)参数向量ϑ的辅助模型梯度迭代算法(AM-GI算法):

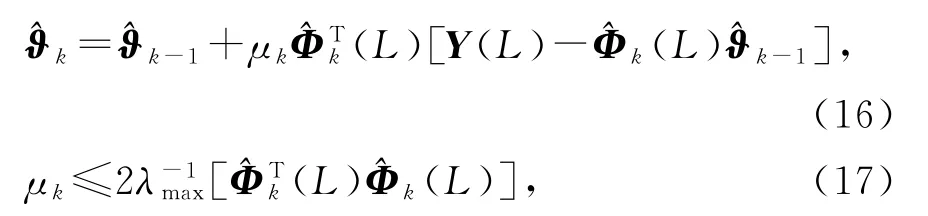
或

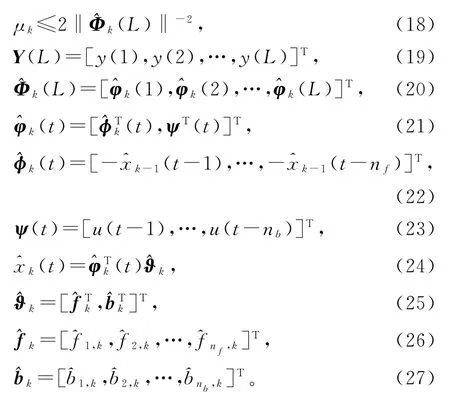
AM-GI算法(16)～(27)计算参数估计的步骤如下。

1)初始化:当t≤0时,所有变量的值都设为零。令k＝1,给定数据长度L和参数估计精度ε,置初值或随机向量,其中1n是一个元均为1的n维列向量或随机数,t＝1,2,…,L。

2)采集输入输出数据u(t)和y(t),用式(23)构造信息向量ψ(t),t＝1,2,…,L。用式(19)构造堆积输出向量Y(L)。

3)用式(22)构造输出信息向量(t),用式(21)构造信息向量(t),t＝1,2,…,L。用式(20)构造堆积信息矩阵(L)。

4)根据式(17)和(18)选择一个尽可能大的步长μk,用式(16)刷新参数估计。

5)从式(25)的中提取参数估计和。用式(24)计算辅助模型输出(t),t＝1,2,…,L。

算法的参数估计精度依赖于数据长度L,因此数据长度应该足够大。取收敛因子在消除中间变量Y(L)和(L)后,AM-GI算法(16)～(27)可等价表示为

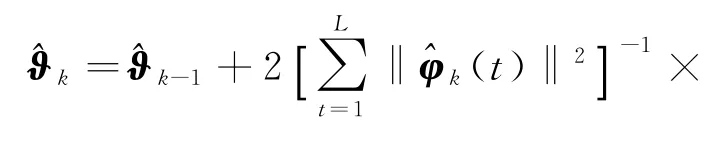
AM-GI算法(28)～(35)计算参数估计的步骤如下。

1)初始化:当t≤0时,所有变量的值都设为零。令k＝1,给定数据长度L和参数估计精度ε,置初值＝1n/p0或随机向量,其中1n是一个元均为1的n维列向量或随机数,t＝1,2,…,L。

2)采集输入输出数据u(t)和y(t),用式(31)构造信息向量ψ(t),t＝1,2,…,L。

3)用式(30)构造输出信息向量(t),用式(29)构造信息向量(t),t＝1,2,…,L。

4)用式(28)刷新参数估计。

5)用式(32)计算辅助模型的输出(t),t＝1,2,…,L。

3 辅助模型最小二乘迭代算法

令输出误差系统(1)的最小二乘准则函数J1(ϑ)对参数向量ϑ的偏导数为零:

假设φ(t)是持续激励的,对于大L,[ΦT(L)Φ(L)]是可逆矩阵,那么从上式可以求得参数向量ϑ的最小二乘估计:

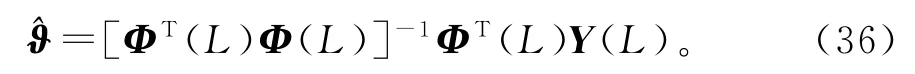
然而,一个类似的问题出现:上式中Φ(L)是未知的,所以式(36)无法计算出参数估计。为了解决这个问题,用式(12)中(L)代替式(36)中的未知矩阵Φ(L),得到式(37)中的最小二乘迭代估计,联立式(19)～(27),便得到辨识输出误差系统(1)参数向量ϑ的辅助模型最小二乘迭代算法(AM-LSI算法):

AM-LSI算法(37)～(46)计算最小二乘参数估计的步骤如下。

1)初始化:当t≤0时,所有变量的值都设为零。令k＝1,给定数据长度L和参数估计精度ε,置(t)为随机数,t＝1,2,…,L。随机数初值是为保证式(37)中矩阵可逆。

2)采集输入输出数据u(t)和y(t),用式(42)构造信息向量ψ(t),t＝1,2,…,L。用式(38)构造堆积输出向量Y(L)。

4)用式(37)刷新参数估计。

5)用式(43)计算辅助模型的输出(t),t＝1,2,…,L。

6)比较和:如果就增加1,转到步骤3);否则获得参数估计向量,中断循环计算过程。

4 辅助模型多新息梯度迭代算法

辨识模型(6)中信息向量φ(t)是未知的,因为其除了包含系统可测输入数据u(t－i),还包含了未知无噪输出变量x(t－i),这是输出误差系统辨识的困难。解决的方法是利用系统的可测信息(包括计算得到的信息)建立一个辅助模型,用辅助模型的输出(t－i)定义φ(t)的迭代估计:

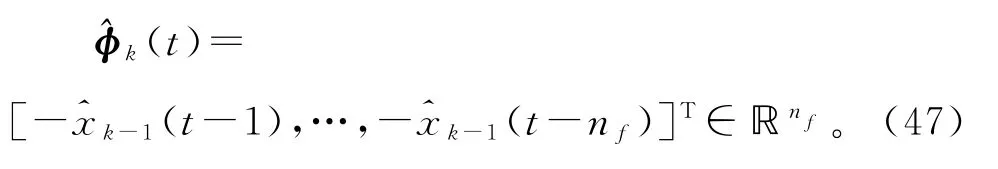
用ψ(t)、φ(t)的估计(t)构造φ(t)的估计:

由式(4)可得

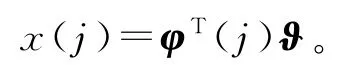
(t)可作x(t)在时刻t的第k次迭代估计。

考虑长度为p的数据窗,它随时间t的增加不断向前移动,故也称为移动数据窗或滑动数据窗(moving data window,MDW)。在递推辨识中,基于移动数据窗的辨识方法包括有限数据窗(递推)最小二乘算法,多新息随机梯度算法,多新息最小二乘算法等。移动数据窗准则函数和多新息准则函数有密切关系,故在迭代辨识中,基于移动数据窗的迭代辨识算法也称为多新息迭代辨识算法,如移动数据窗梯度迭代算法又称为多新息梯度迭代算法,移动数据窗最小二乘迭代算法又称为多新息最小二乘迭代算法,移动数据窗牛顿迭代算法又称为多新息牛顿迭代算法等。

设移动数据窗长度为p。考虑从j＝t－p＋1到j＝t的p组数据,定义堆积输出向量Y(p,t)和堆积信息矩阵Φ(p,t)如下:

根据辨识模型(6),定义滑动数据窗准则函数:

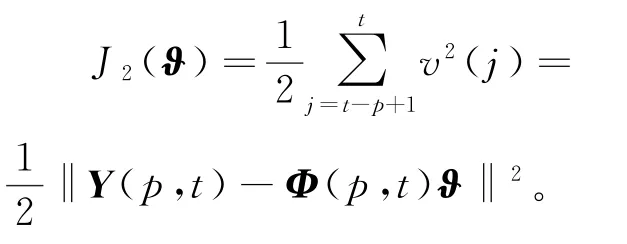
令k＝1,2,3,…,是一个迭代变量,μk(t)为迭代步长(收敛因子)。使用负梯度搜索,极小化准则函数J2(ϑ),得到下列梯度迭代关系:

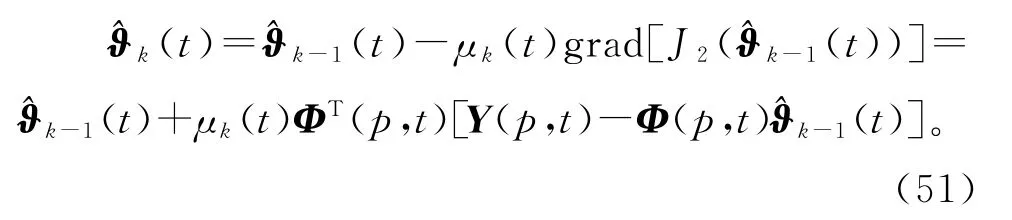
用φ(t)的估计(t)构造堆积信息矩阵Φ(p,t)的估计:

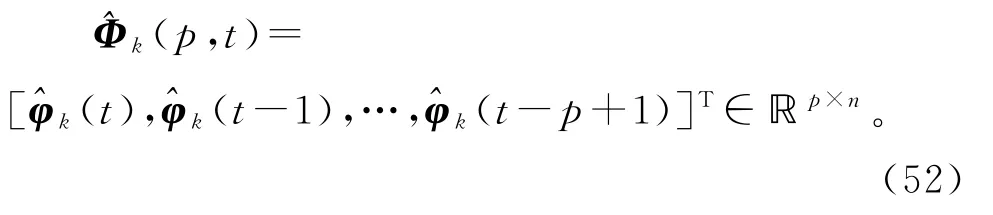
用(p,t)代替式(51)中矩阵Φ(p,t)可得

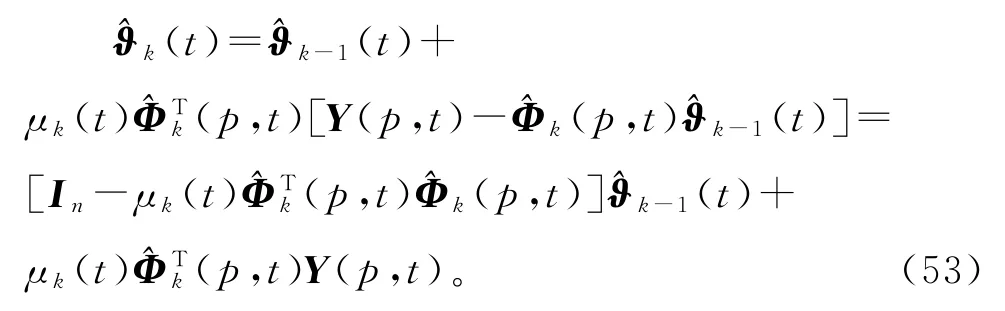
式(53)可以看作状态为(t)的离散时间系统(t看作常量),为保证参数估计(t)收敛,系统矩阵的所有特征值必须在单位圆内,因此μk(t)的一个保守选择是满足

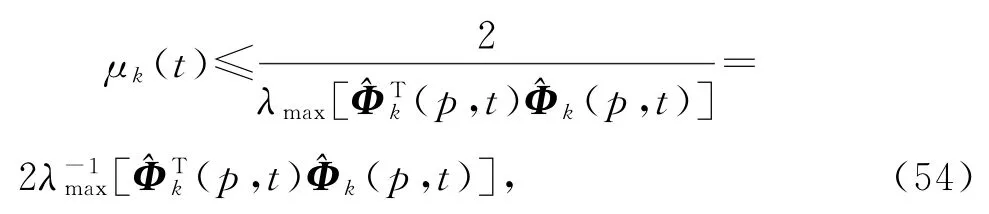
或

联立式(53)～(55),(50),(52),(48),(47)和(3),以及辅助模型(49),就得到辨识输出误差系统(1)参数向量ϑ的辅助模型多新息梯度迭代算法(AM-MIGI算法):

或

AM-MIGI算法(56)～(67)计算参数估计(t)的步骤如下。

1)初始化:当t≤0时,所有变量的值都设为零。令t＝1,给定移动数据窗长度p(通常取p≫n),参数估计精度ε,最大迭代次数kmax。置参数估计初值(t)＝1n/p0或随机向量,其中1n是一个元均为1的n维列向量,p0＝106。

2)令k＝1,采集观测数据u(t)和y(t)。置(j)＝1/p0或随机数,j＝1,2,…,t。用式(63)构造信息向量ψ(t),用式(59)构造堆积输出向量Y(p,t)。

3)用式(62)构造信息向量(t),用式(61)构造信息向量(t),用式(60)构造堆积信息矩阵(p,t)。

4)根据式(57)或(58)选择一个尽可能大的步长μk(t),用式(56)刷新参数估计(t)。

5)用式(64)计算辅助模型的输出(j),j＝1,2,…,t。

6)如果k＜kmax,k就增加1,转到步骤3);否则执行下一步。

根据经验,当信息向量中包含需要进行迭代估计的未知量(如噪声项和辅助模型输出项)数目较少时,对于梯度迭代算法,kmax取值一般在几百到上千之间;对于最小二乘迭代算法,一般取kmax＝5 或kmax＝6。当信息向量中包含需要进行迭代估计的未知量较多时,kmax可以选择大一些。

由一次完成最小二乘算法可知,移动数据窗梯度迭代算法和移动数据窗最小二乘迭代算法的参数估计精度取决于数据窗的长度p,为了获得高精度的参数估计,p应足够大。关于内循环的最大迭代次数kmax的选择,当k继续增加,参数估计精度没有明显变化时,就不再增加k,这时的k可作为kmax的选择依据。

5 辅助模型多新息最小二乘迭代算法

令输出误差系统的动态数据窗准则函数J2(ϑ)对参数向量ϑ的偏导数为零:

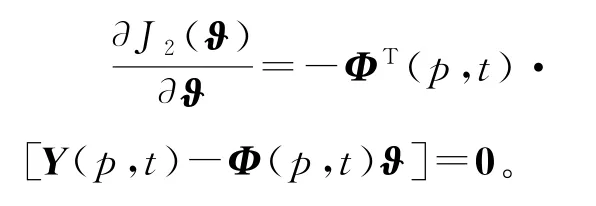
设对于p≫n,假设信息向量φ(t)是持续激励的,[ΦT(p,t)Φ(p,t)]是可逆矩阵,那么可以求得参数向量ϑ的最小二乘估计:

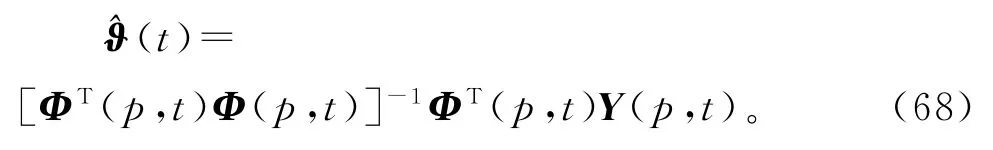
由于上式中矩阵Φ(p,t)是未知的,所以无法计算出参数估计解决的方法是用式(52)中)代替式(68)中Φ(p,t),得到式(69)中的最小二乘迭代估计,联立式(59)～(67),便得到辨识输出误差系统(1)参数向量ϑ 的辅助模型多新息最小二乘迭代算法(AM-MILSI算法):

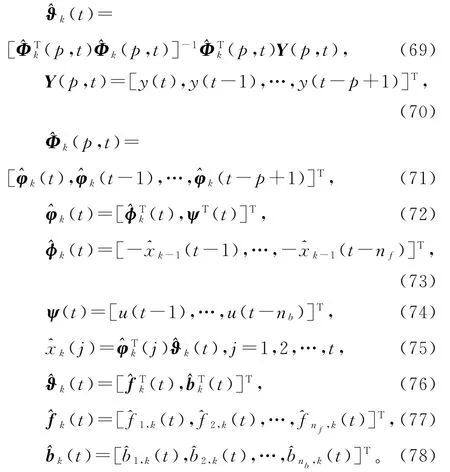
AM-MILSI算法(69)～(78)计算参数估计向量(t)的步骤如下。

1)初始化:假设t≤0时,所有变量的值均为零。给定移动数据窗长度或新息长度p(通常取p≫n),令t＝p,收集输入输出数据{u(j),y(j):j＝0,1,…,p－1},设置参数估计精度ε,最大迭代次数kmax。

2)令k＝1,采集观测数据u(t)和y(t)。置^x0(j)为随机数,j＝1,2,…,t。用式(74)构造信息向量ψ(t),用式(70)构造堆积输出向量Y(p,t)。随机数初值是为保证式(69)中矩阵[(p,t)(p,t)]可逆。

3)用式(73)构造信息向量(t),用式(72)构造信息向量(t),用式(71)构造堆积信息矩阵(p,t)。

7)如果k＜kmax,k就增加1,转到步骤3);否则执行下一步。

6 辅助模型递阶梯度迭代辨识算法

本节研究输出误差系统的辅助模型递阶梯度迭代(AM-HGI)算法、辅助模型递阶最小二乘迭代(AM-HLSI)算法、辅助模型递阶多新息梯度迭代(AM-HMIGI)算法、辅助模型递阶多新息最小二乘迭代(AM-HMILSI)算法。

重写输出误差系统(1):

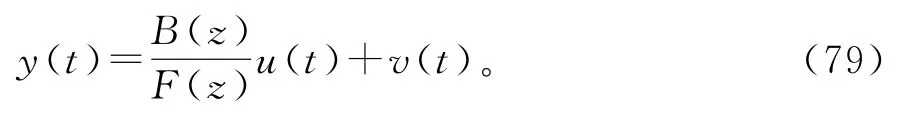
对应的辨识模型为

将输出误差系统分解成两个虚拟子系统,使得算法涉及的协方差矩阵维数减小,能有效地减小迭代算法的计算量。

对输出误差系统辨识模型(81)进行分解,得到两个子辨识模型,一个包含参数向量f,另一个包含参数向量b,分别推导它们的迭代辨识算法,并利用递阶辨识原理协调两个子辨识算法间的关联项。

定义两个虚拟输出:

将输出误差系统的辨识模型(81)分解成两个虚拟子系统(fictitious subsystem):

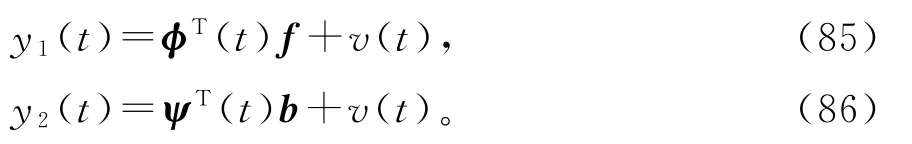
这两式构成了输出误差系统的递阶辨识模型。子系统(85)包含参数向量f,有n f个未知参数,对应的信息向量φ(t)包含了未知中间变量x(t－i);子系统(86)包含参数向量b,有n b个未知参数,对应的信息向量ψ(t)是已知的。

设L为数据长度。使用观测输入输出数据{u(t),y(t):t＝0,1,…,L},定义堆积输出向量Y(L),Y1(L)和Y2(L),堆积信息矩阵Φ(L)和Ψ(L)如下:

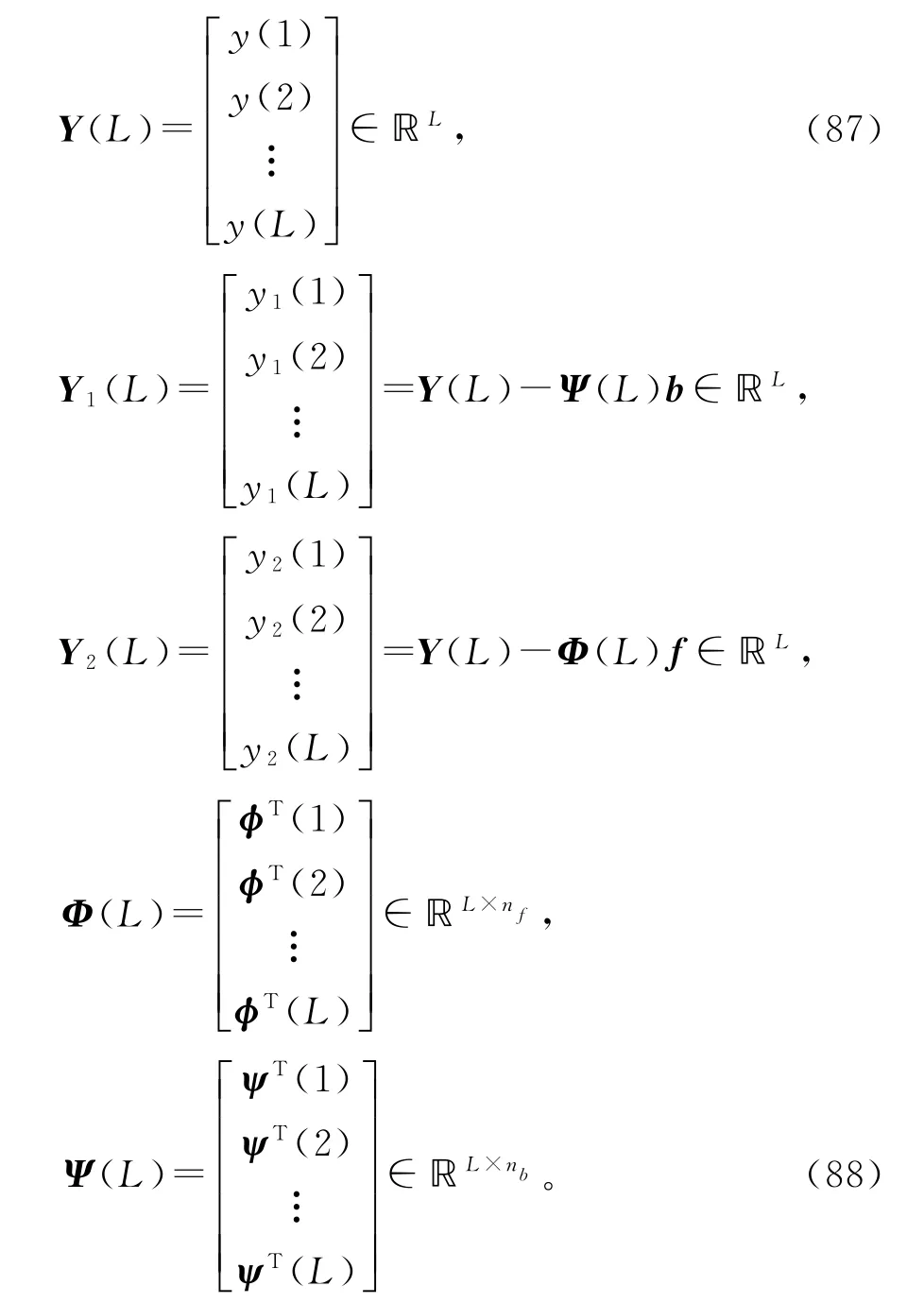
根据递阶辨识模型(85)和(86),定义两个准则函数:

设∈ℝn f是f的第k次迭代估计∈是b的第k次迭代估计,μ1,k≥0和μ2≥0是迭代步长(收敛因子)。使用负梯度搜索,极小化准则函数J3(f)和J4(b),得到关于参数估计和的梯度迭代关系:

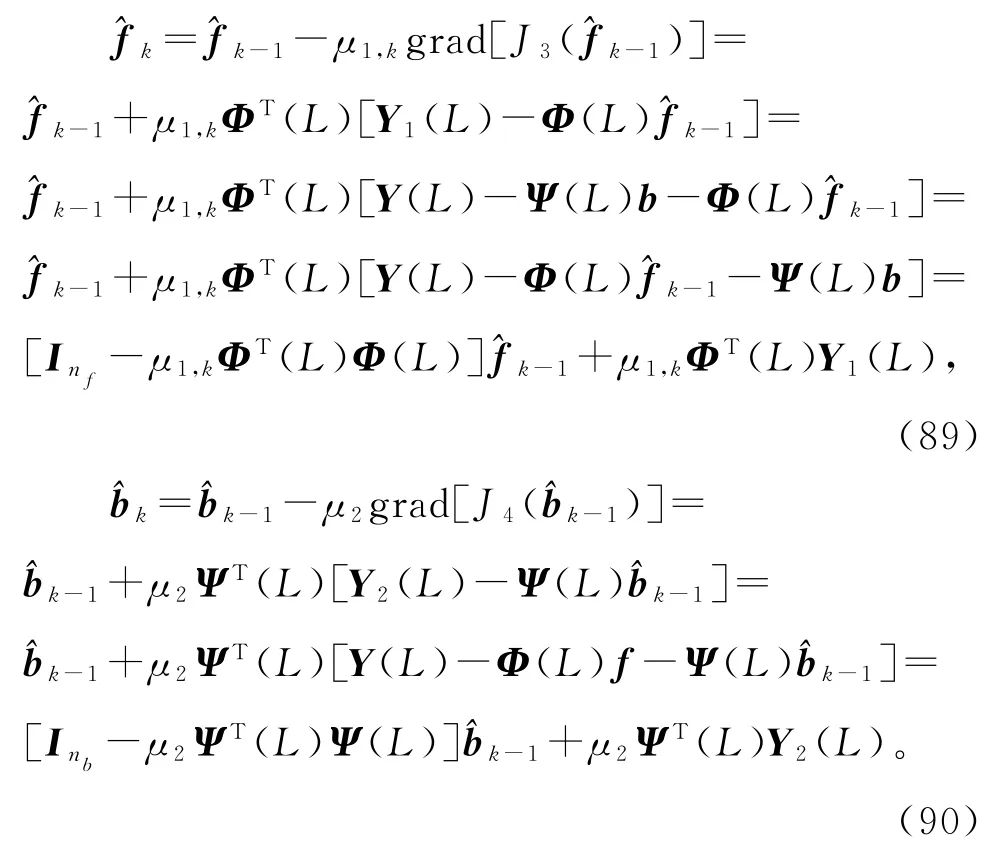
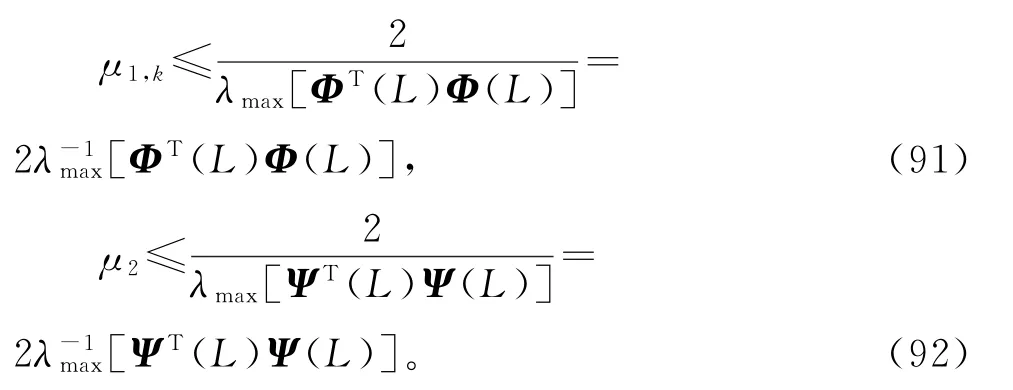
收敛因子也可简单取为

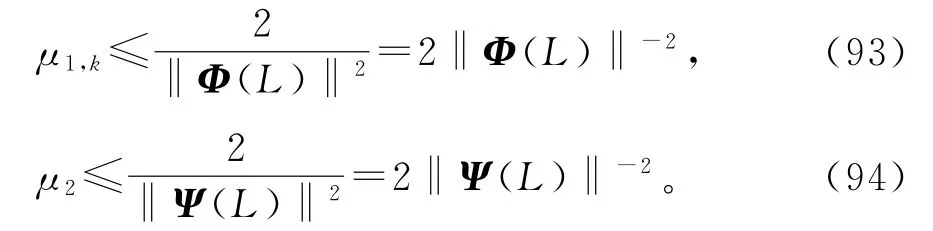
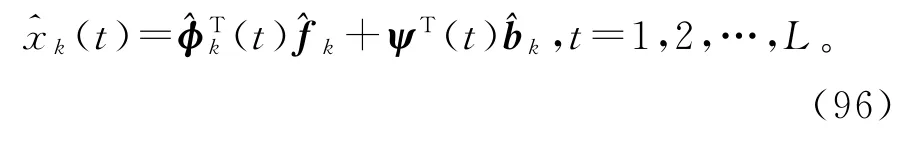
(t)可作为x(t)在时刻t的第k次迭代估计。根据堆积信息矩阵Φ(L)定义式的结构,用φ(t)的估计^φk(t)定义Φ(L)的估计:

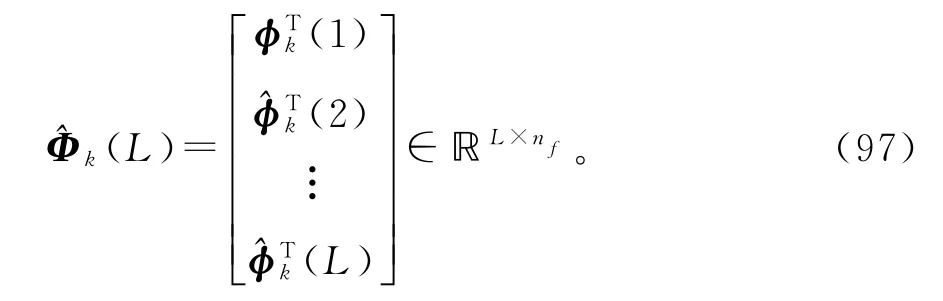
采用递阶辨识原理,式(89)～(94)右边未知的信息矩阵Φ(L)用其估计(L)代替,未知参数向量b和f分别用其估计和代替,得到式(98)～(103),联立式得到式(87)～(88),(97),(82),和(95)～(96),便得到辨识输出误差系统(79)参数向量f和b的辅助模型递阶梯度迭代算法(AM-HGI算法):

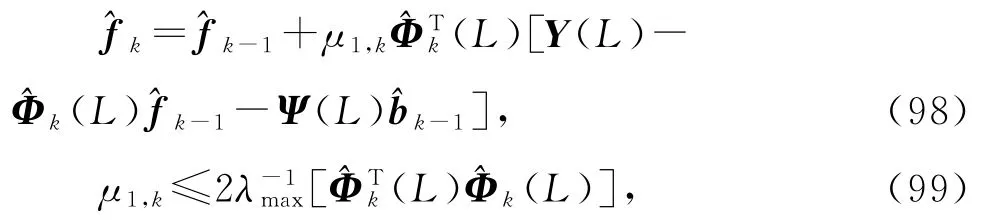
或

或

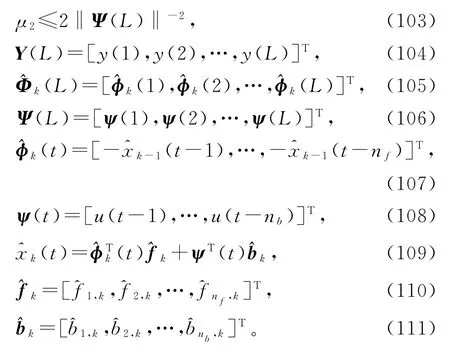
AM-HGI算法(98)～(111)计算参数估计的步骤如下。

1)初始化:当t≤0时,所有变量的值都设为零。令k＝1,给定数据长度L≫n和参数估计精度ε,置初值或随机向量＝1nb/p0或随机向量,其中1n是一个元均为1的n维列向量,p0＝106。置(t)＝1/p0或随机数,t＝1,2,…,L。

2)采集输入输出数据u(t)和y(t),用式(108)构造ψ(t),t＝1,2,…,L。用式(104)构造堆积输出向量Y(L),用式(106)构造Ψ(L)。根据式(102)或(103)确定一个尽量大的步长μ2。

3)用式(107)构造输出信息向量(t),t＝1,2,…,L。用式(105)构造堆积信息矩阵(L)。

4)根据式(99)或(100)确定一个尽量大的步长μ1,k。用式(98)刷新参数估计^f k,用式(101)刷新参数估计。

5)利用式(109)计算辅助模型的输出(t),t＝1,2,…,L。

7 辅助模型递阶最小二乘迭代算法

令准则函数J3(f)和J4(b)分别对参数向量f和b的偏导数为零:

设数据长L≫n,信息向量φ(t)和ψ(t)是持续激励的,即[ΦT(L)Φ(L)]和[ΨT(L)Ψ(L)]是可逆矩阵,由可求得估计:

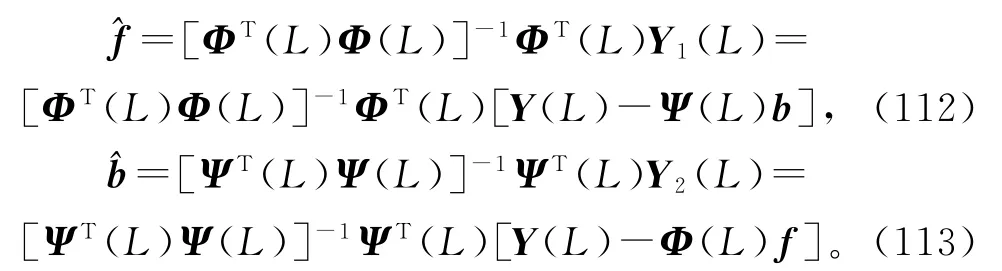
式(112)～(113)无法直接计算估计和,因为右边包含了未知矩阵Φ(L),未知参数向量b和f。解决的办法是用式(97)中的(L),以及前一次迭代参数估计和代替式(112)～(113)右边的未知信息矩阵Φ(L),以及未知参数向量b和f,得到式(114)～(115)的最小二乘迭代估计和,联立(104)～(111),便得到辨识输出误差系统(79)参数向量f和b的辅助模型递阶最小二乘迭代算法(AM-HLSI算法):

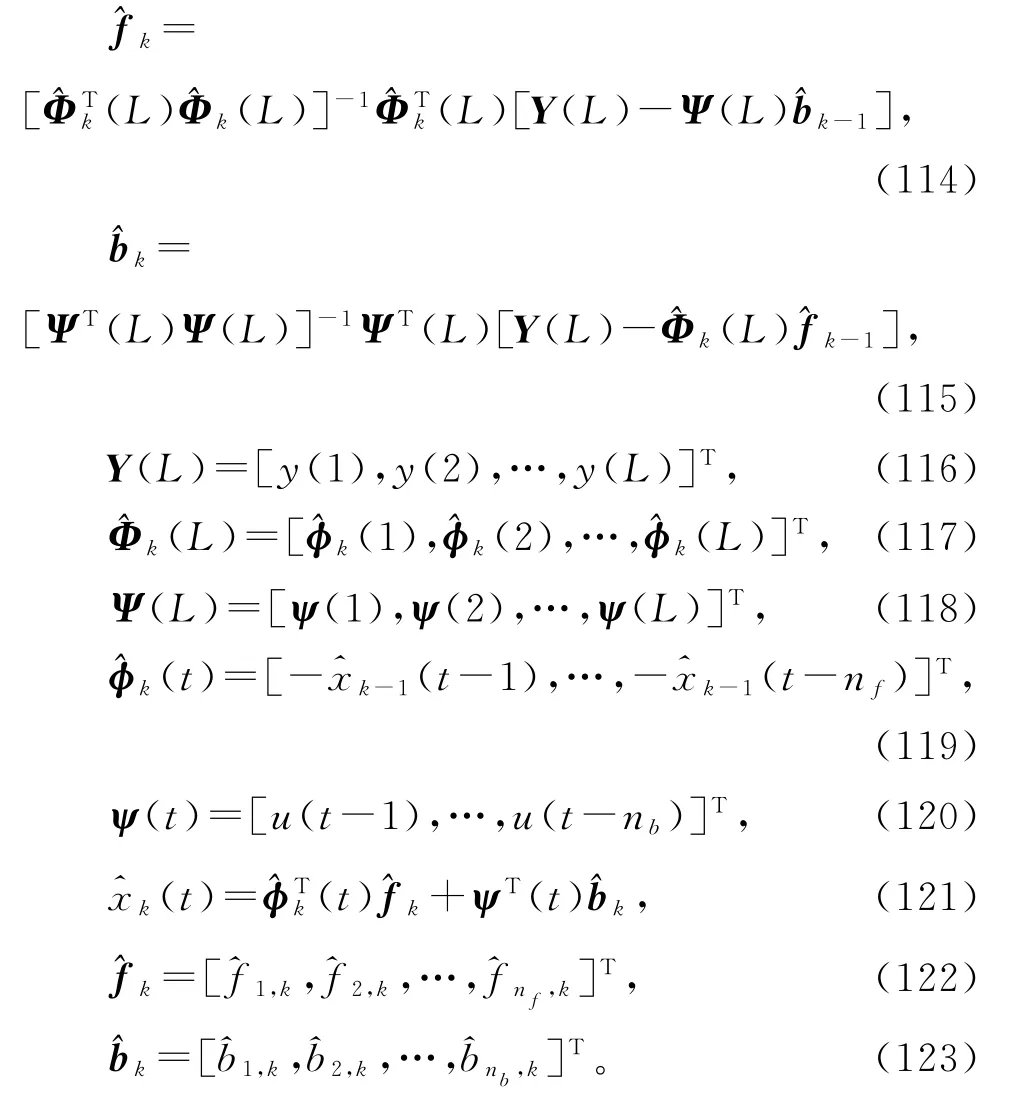
AM-HLSI算法(114)～(123)计算参数估计的步骤如下。

1)初始化:当t≤0时,所有变量的值都设为零。令k＝1,给定数据长度L≫n和参数估计精度ε,置初值＝/p0或随机向量＝1nb/p0或随机向量,置(t)为随机数,t＝1,2,…,L。

2)采集输入输出数据u(t)和y(t),用式(120)构造ψ(t),t＝1,2,…,L。用式(116)构造堆积输出向量Y(L),用式(118)构造堆积信息矩阵Ψ(L)。

3)用式(119)构造输出信息向量(t),t＝1,2,…,L。用式(117)构造(L)。

4)用式(114)刷新参数估计,用式(115)刷新参数估计。

8 辅助模型递阶多新息梯度迭代算法

设p为新息长度或移动数据窗长度。使用直到当前时刻t的p组数据,定义堆积输出向量Y(p,t),Y1(p,t)和Y2(p,t),堆积信息矩阵Φ(p,t)和Ψ(p,t)如下:

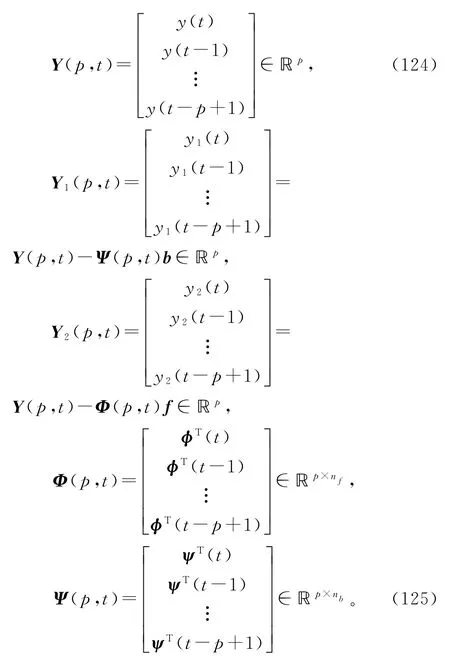
根据子系统辨识模型(85)和(86),定义两个动态数据窗准则函数:

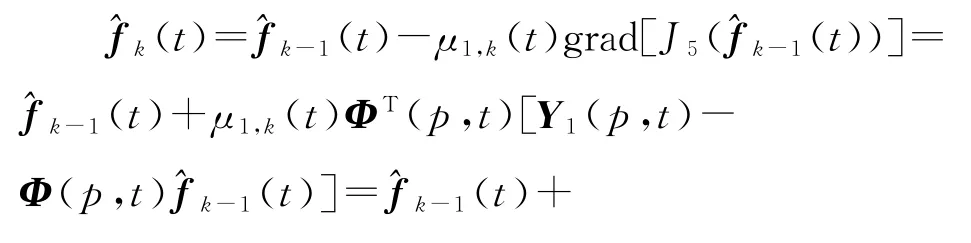
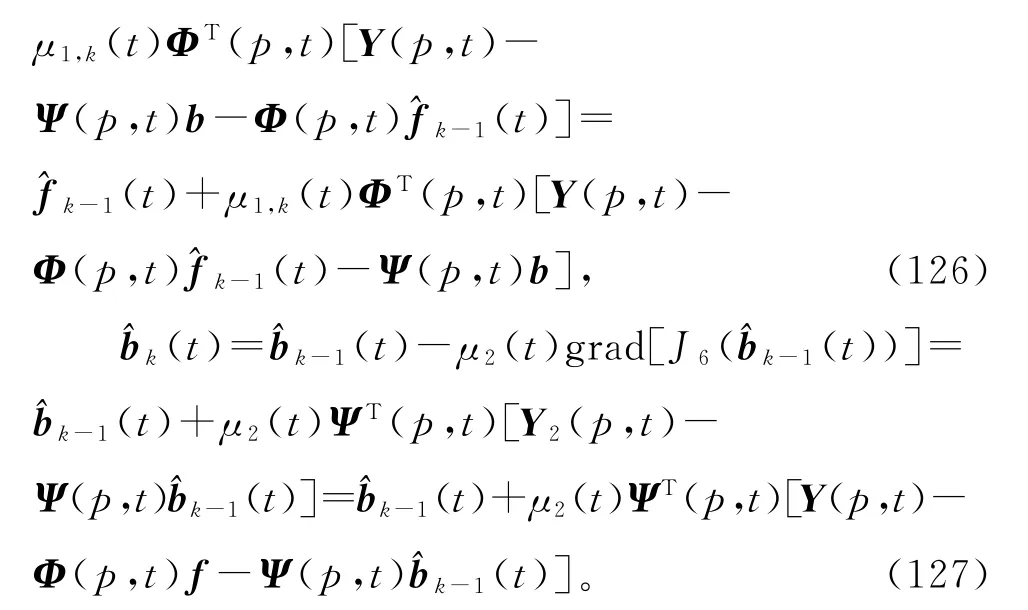
或简单取为

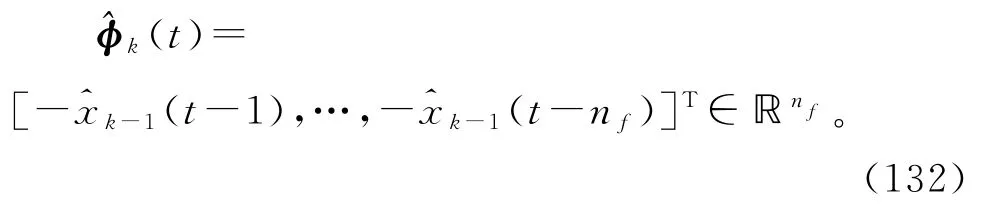
由式(80)可得

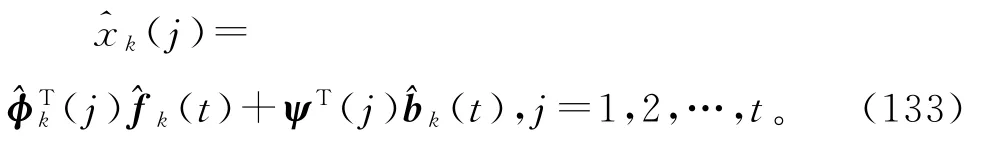
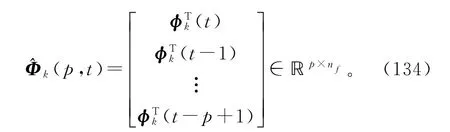
采用递阶辨识原理,式(126)～(131)右边未知信息矩阵Φ(p,t)用其估计(p,t)代替,未知参数向量b和f分别用其估计代替,得到式(135)～(140),联立式(124)～(125),(134),(82)和(132)～(133),便得到辨识输出误差系统(79)参数向量f和b的辅助模型递阶多新息梯度迭代算法(AM-HMIGI算法):

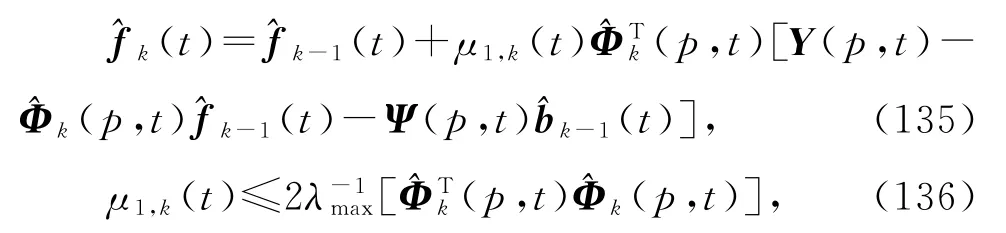
或

或

取p＝t＝L时,AM-HMIGI辨识算法(135)～(148)退化为AM-HGI辨识算法(98)～(111)。

AM-HMIGI算法(135)～(148)计算参数估计的步骤如下。

1)初始化:假设在t≤0 时所有变量取值均为零。令t＝1,给定移动数据窗长度p(通常取p≫n),参数估计精度ε,最大迭代次数kmax。置初值或随机向量或随机向量,其中1n是一个元均为1的n维列向量,p0＝106。

2)令k＝1,置(j)＝1/p0或随机数,j＝1,2,…,t。采集输入输出数据u(t)和y(t)。用式(145)构造ψ(t),用式(141)构造堆积输出向量Y(p,t),用式(143)构造堆积信息矩阵Ψ(p,t),根据式(139)或(140)确定一个尽量大的步长μ2(t)。

6)如果k＜kmax,k就增加1,转到步骤3);否则执行下一步。

9 辅助模型递阶多新息最小二乘迭代算法

令准则函数J5(f)和J6(b)分别对参数向量f和b的偏导数为零:

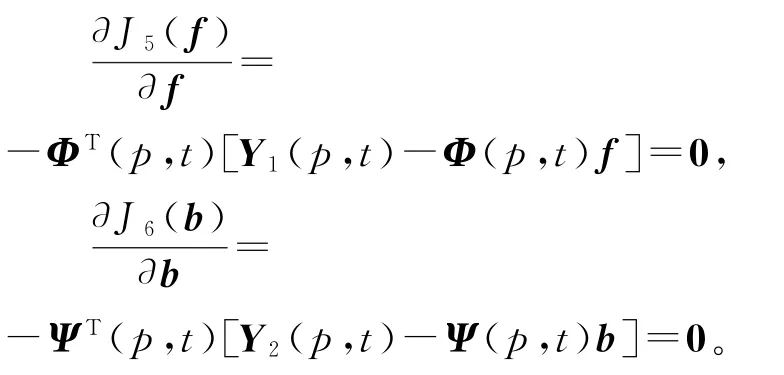
设数据长p≫n,信息向量φ(t)和ψ(t)是持续激励的,即[ΦT(p,t)Φ(p,t)]和[ΨT(p,t)Ψ(p,t)]是可逆矩阵,可求得估计:

式(149)～(150)无法直接计算估计和,因为右边包含了未知矩阵Φ(p,t),未知参数向量b和f。解决的办法是用式(134)中的(p,t),以及前一次迭代参数估计(t)和(t)代替式(149)～(150)右边的未知信息矩阵Φ(p,t),以及未知参数向量b和f,得到式(151)～(152)的最小二乘迭代估计(t)和(t),联立(141)～(148),便得到辨识输出误差系统(79)参数向量f和b的辅助模型递阶多新息最小二乘迭代算法(AMHMILSI算法):

取p＝t＝L时,AM-HMILSI辨识算法(151)～(160)退化为AM-HLSI辨识算法(114)～(123)。

AM-HMILSI算法(151)～(160)计算参数估计的步骤如下。

1)初始化:假设在t≤0 时所有变量取值均为零。令t＝l,给定移动数据窗长度p(通常取p≫n),参数估计精度ε,最大迭代次数kmax,置初值(t)＝1n/p0或随机向量(t)＝1n/p0或随机向量,其中1n是一个元均为1的n维列向量,p0＝106。采集观测数据{u(j),y(j):j＝0,1,…,l－1}。这里l≥p为一个正整数(请思考l的意义)。

2)令k＝1,置(j)为随机数,j＝1,2,…,t。采集输入输出数据u(t)和y(t)。用式(157)构造ψ(t),用式(153)构造堆积输出向量Y(p,t),用式(155)构造堆积信息矩阵Ψ(p,t)。

3)用式(156)构造输出信息向量(t),用式(154)构造堆积信息矩阵(p,t)。

7)如果k＜kmax,k就增加1,转到步骤3);否则执行下一步。

10 结 语

以输出误差模型为例,基于辅助模型辨识思想和迭代搜索原理,研究了辅助模型(多新息)梯度迭代辨识算法和辅助模型(多新息)最小二乘迭代辨识算法,进一步利用递阶辨识原理,通过极小化两个最小二乘准则函数,研究了辅助模型递阶(多新息)梯度迭代辨识算法和辅助模型递阶(多新息)最小二乘迭代辨识算法等。提出的分解辨识思想可以推广到大规模线性随机系统和复杂非线性随机系统的迭代辨识,其干扰可以是有色噪声。