连续操作密相流化床颗粒停留时间分布特性模拟放大研究

2021-01-30兰斌徐骥刘志成王军武

化工学报 2021年1期

兰斌，徐骥，刘志成，王军武

（1 中国科学院过程工程研究所多相复杂系统国家重点实验室，北京100190； 2 中国科学院大学化学工程学院，北京100049； 3 中国科学院绿色过程制造创新研究院，北京100190； 4 中国石油化工股份有限公司上海石油化工研究院，上海201208）

引言

气固流化床因具有良好的气固接触效率、较高的传质传热效率和气固处理能力而被广泛应用于石油催化裂化反应、金属矿物的焙烧与还原、化石燃料的燃烧、生物质的热解和气化以及造粒等过程[1-5]。然而，由于气体和颗粒间的复杂作用使得人们至今难以对流化床内气固两相流流场进行精确的分析，到目前为止工业流化床反应器的设计和放大还主要通过实验逐级放大的方法。但是逐级放大实验成本高、周期长，因此随着计算机的发展，研究人员开始采用CFD 数值模拟的方法对流化床的放大效应进行研究[6-11]。

目前研究流化床模拟放大主要采用以下两类方法：欧拉-欧拉双流体模型（two-fluid model，TFM）和欧拉-拉格朗日CFD-DEM 模型及其简化方法。例如Verma 等[6]、Che 等[7]采用TFM 研究了流化床直径对气泡和固体运动、环-核结构的影响。Couto等[8]采用耦合k-ε 湍流模型的TFM 方法研究了实验室和半工业生物质气化反应器的气化温度、氧气含量和生物质类型对反应的影响，发现反应器尺寸越大，气体停留时间越长，气化反应越充分，CO 和H2的含量越高，合成气热值越高。Lu 等[9]采用EMMS曳力模型预测了四种不同尺度的甲醇制取烯烃反应器的流动特性，认为化学反应动力学模型通常是通过对微尺度流化床实验数据进行拟合得到的，可能并不适用于较大尺寸的反应器。Zhang 等[10]采用CFD-DEM 方法证明了在保证流化床底部进口气流均匀的情况下，增加流化床长度对煤和煤矸石颗粒分离程度的影响并不大。此外，Gu 等[11]采用多相流质点网格法（multiphase particle-in-cell，MP-PIC）对循环流化床（circulating fluidized bed，CFB）锅炉内的气固流动和富氧燃烧过程进行了研究，发现实验室和中试流化床颗粒速度场比工业流化床更加均匀，工业CFB 锅炉的CO、NO 和SO2排放量低于实验室和中试锅炉，热量输入的增加可以提高脱硫效率。

颗粒停留时间分布（residence time distribution，RTD）是表征反应器内气固混合程度的重要参数，近几十年来，研究人员分别利用实验、理论和数值模拟手段来研究气固流化床，特别是密相连续操作流化床内颗粒停留时间分布情况[12-15]。实验方面，白书培等[12]发现在气速、粒径、床高、颗粒流量等操作条件中，气速是影响停留时间分布的主要因素，随着气速的增加，颗粒在床内的混合加剧，气速达到一定值时，RTD 曲线出现多峰。但高巍等[13]认为颗粒流率、床高、粒径分布是影响颗粒RTD 的主要因素，气速则是次要因素。颗粒进料流率也是影响颗粒RTD 的重要因素，流率越大，颗粒停留时间越短，颗粒流动向平推流靠近[13]。Matheson 等[14]发现相比粗颗粒，细颗粒在床内的混合程度更强，粗颗粒停留时间分布更趋于平推流[13]。不同粒径颗粒在流化床中停留时间存在差异，随着颗粒粒径的增加，颗粒平均停留时间增长[15]，同一流化床内粗颗粒比细颗粒停留时间更长[16]。Yagi 等[17]发现，如果颗粒转化受化学反应的控制（最有可能发生在细颗粒转化中），则完全转化时间与颗粒粒径呈正比；如果颗粒转化受内扩散控制（最有可能发生在粗颗粒转化中），则完全转化时间与颗粒粒径的平方呈正比。郝志刚等[18]采用多级横向内构件研究了粒径分布较宽的颗粒平均停留时间，发现700 μm 颗粒平均停留时间是108 μm颗粒的5倍。数值模拟方面，Geng等[19]、Zou 等[20-21]、Hua 等[22]采用TFM 研究了固体流率、气速、床高、示踪剂注入时间、取样频率等操作条件对颗粒停留时间分布的影响。Zou 等[23]、Hua等[24]发现相比均匀结构曳力模型，非均匀结构曳力模型预测的颗粒停留时间分布和实验结果吻合得更好。Börner 等[25]提出一种基于相似性模型的放大方法，模拟了气、液、固三相顶部喷雾造粒机内颗粒的停留时间分布，发现颗粒所穿过的喷雾区长度和颗粒速度的变化导致颗粒停留时间不同。Zhao等[26]、Lu等[27]采用CFD-DEM 方法模拟了循环流化床提升管内颗粒的返混行为。Lan 等[28-29]提出了局部返混指数的概念，采用CPFD 方法研究了循环流化床中不同流型颗粒返混特性以及提升管出口结构对颗粒停留时间的影响，指出相对于简单出口和C型出口，含有L 型和T 型出口的提升管内返混程度更为剧烈，停留时间也更长。系统的流化床颗粒停留时间研究进展见文献[30]。

颗粒形状[31-35]和多分散性[36-38]对颗粒的流体力学特性和停留时间分布具有重要影响，为了探究多分散流化床的放大规律，实现流化床的合理放大，本文以非球形、多分散颗粒曳力模型为基础[39]，采用基于GPU 大规模并行的粗粒化CFD-DEM 方法[40]，研究连续进出料流化床颗粒停留时间和流动特性随流化床尺寸的变化关系。

1 数学模型

1.1 粗粒化CFD-DEM 方法

本文所采用的粗粒化CFD-DEM 方法是基于Lu等[40]提出的基于能量最小多尺度离散颗粒方法（energy minimization multi-scale-discrete particle method，EMMS-DPM），但与EMMS-DPM 方法有以下几个区别。

（1）假设粗颗粒（coarse grained particle,CGP）的密度等于真实颗粒的密度，即粗颗粒质量mCGP=k3mp，其中，mp是真实颗粒质量，k 是粗粒化率，k=dCGP/dp。而原始EMMS-DPM 方法中的粗颗粒内部存在空隙，其空隙率等于最小流化条件下的空隙率。

（2）实验采用不规则形状的石英砂颗粒，对于非球形颗粒与颗粒/壁面之间接触力的计算，可以通过组合球元构建非球形颗粒几何模型的方法实现[41]，但需要计算大量球元之间的碰撞，计算量明显增大。因此，为提高计算速度，在计算颗粒与颗粒/壁面之间相互作用时，仍将颗粒视为球形。颗粒之间碰撞作用的计算采用Peng等[42]提出的方法。

（3）在CFD-DEM 模型中，气固相间作用力占主导地位[43]。有研究指出[33]，当颗粒球形度Ψ=1 时，原始的Ergun 曳力系数关联式（黏性项系数为150，惯性项系数为1.75）可以很好地预测含球形颗粒的流化床的压降；但对于非球形颗粒（Ψ≠1），只有当颗粒形状接近球形时，Ergun 关系式才能较为准确地预测其曳力，因此采用Ganser非球形颗粒曳力模型[33,44]来计算单颗粒曳力系数CD，并将其引入Di Felice 曳力模型中[45]，具体曳力系数的计算见1.4节。

（4）在气固曳力模型中考虑颗粒的多分散性，参照Beetstra 等[46]、Zhou 等[47]对多分散系统曳力的处理方式，对曳力模型进行修正，计算不同粒径颗粒所受曳力。

由此可以看出在计算颗粒之间碰撞作用时将颗粒视为球形，而在计算气固相间曳力时模拟真实颗粒，即引入颗粒球形度这一物理量[通过式（30）、式（31）估算得到球形度的值，此值也符合石英砂颗粒球形度的取值范围]。这是因为本课题组前期的尝试表明，如果曳力中不引入球形度的影响，将得到完全错误的模拟结果，但是如果在颗粒碰撞时考虑球形度，则计算量将大幅度增加。因此，本文采用的是一种兼顾计算准确性和计算效率的折中近似方案。

1.2 控制方程

气相连续性方程

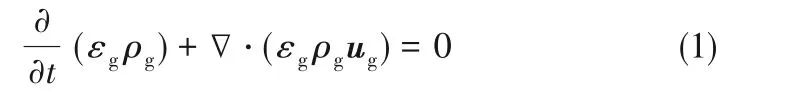
式中，ug为气相速度，m/s;εg为空隙率。

气相动量方程

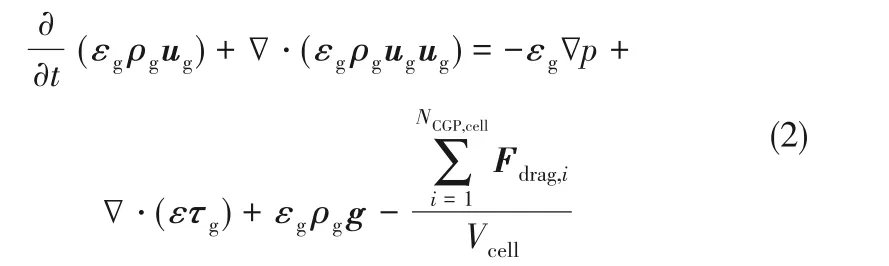
其中，气相应力张量为

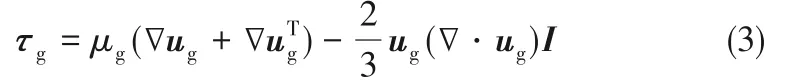
式中，NCGP,cell为网格中粗颗粒数目；Vcell为网格体积，m3;I为单位张量。

颗粒平动方程

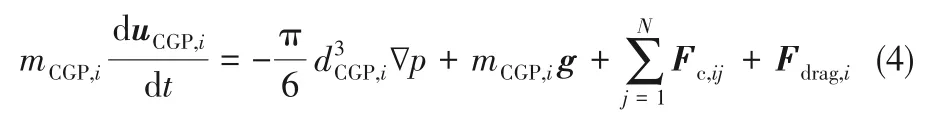
式中，uCGP,i为粗颗粒速度，m/s；右侧四项分别为粗颗粒所受压力梯度力、重力、接触力和曳力，N 为某一时刻与颗粒i同时相互作用的颗粒总数。

颗粒转动方程

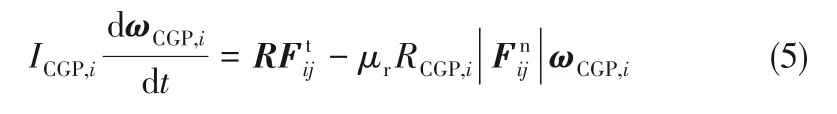
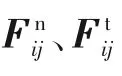
1.3 颗粒碰撞模型

粗颗粒之间碰撞力的计算采用弹簧-阻尼模型，颗粒所受接触力等于法向接触力和切向接触力之和，即

颗粒i与j的法向接触力为

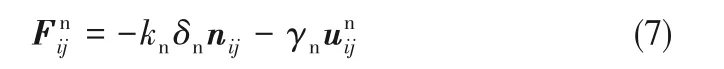
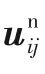
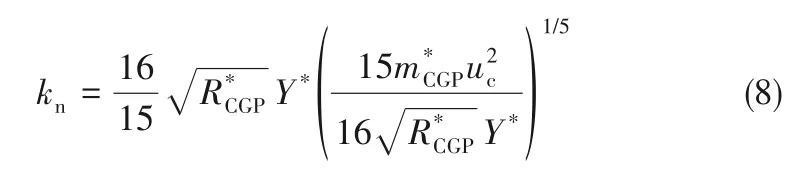
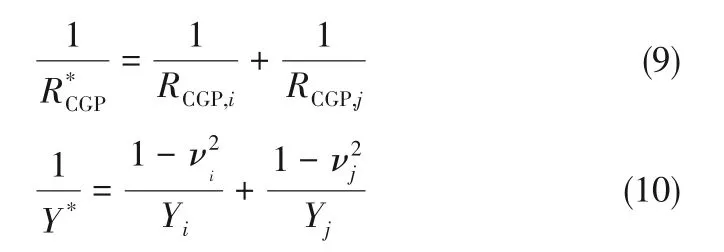
式中，νi、νj为颗粒i和颗粒j的泊松比。

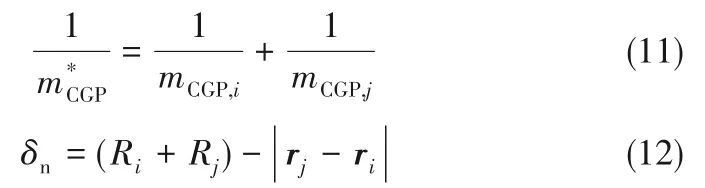
式中，Ri、Rj为颗粒i和颗粒j的半径；ri、rj代表颗粒i和颗粒j的位置矢量。

法向阻尼系数

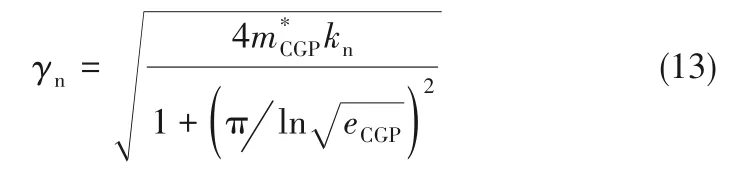
粗颗粒恢复系数

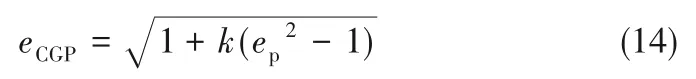
式中，ep为真实颗粒恢复系数。

颗粒i与颗粒j的相对速度

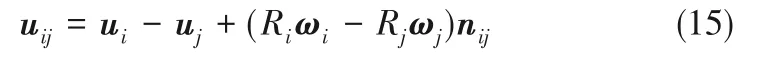
颗粒i与颗粒j的法向相对速度

颗粒i与颗粒j的切向接触力

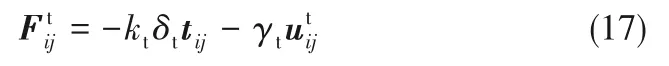
在模拟中还需考虑滑动摩擦力的限制

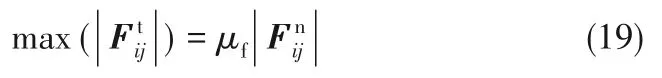
式中，μf为滑动摩擦系数。

1.4 气固曳力模型

本文采用的曳力系数以Di Felice 曳力系数为基础[45]

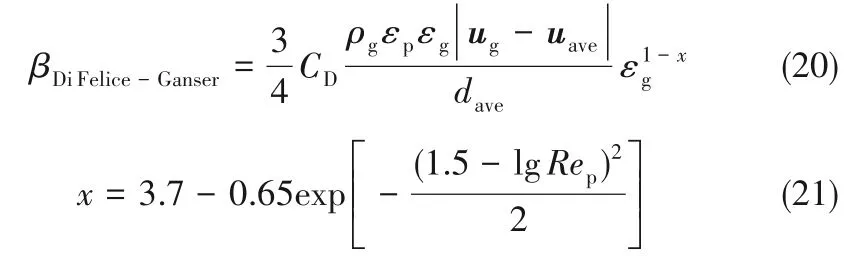
式中，dave为网格中真实颗粒平均直径，m;uave为网格中颗粒平均速度，m/s；εp为网格中颗粒体积分数。

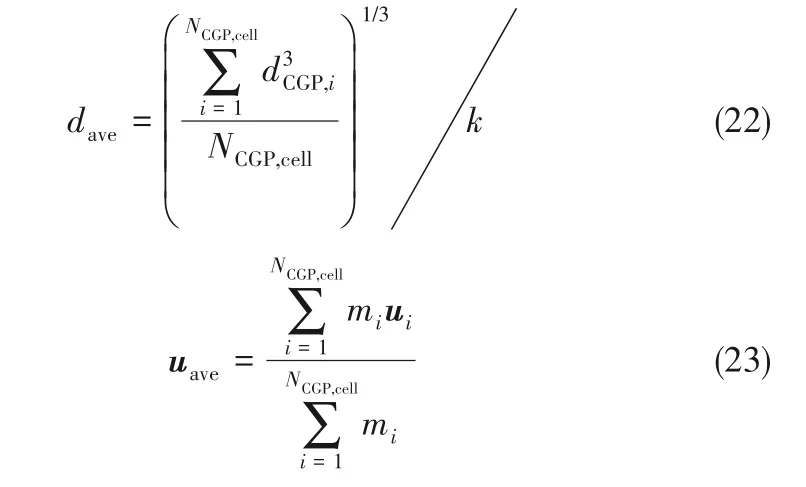
式中，k 为粗粒化率；mi为粗颗粒质量；ui为粗颗粒速度。

其中，单颗粒曳力系数[33,44]

颗粒Reynolds数

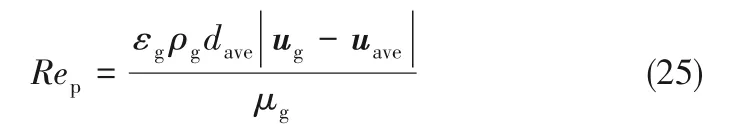
Stokes形状因子

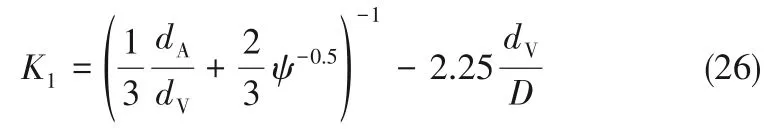
式中，ψ 为颗粒球形度；D 为流化床水力直径，m；dA为等投影面积球当量直径，m；dV为等体积球当量直径，m。由于dA、dV很难通过实验测得，故假设dA=dV=dsauter，dsauter为颗粒Sauter平均直径。

牛顿形状因子

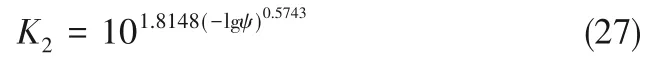
在考虑颗粒非球形影响的Di Felice-Ganser 曳力基础上，引入Beetstra 等[46]的方法考虑颗粒多分散性的影响，则系统中组分j的曳力系数可表示为

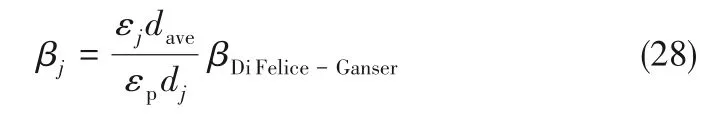
式中，εj代表网格中组分j 的体积分数；dj代表组分j的颗粒直径。

因此，粗颗粒所受曳力为

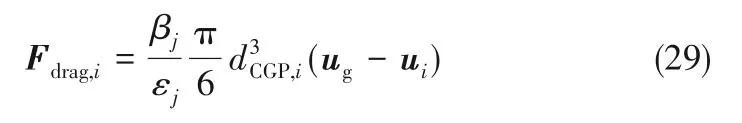
2 流化床放大方式与模拟设置

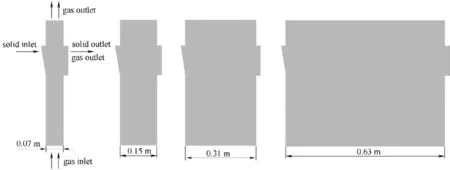
图1 三维连续进出料流化床装置模拟Fig.1 Simulation schematic diagram of 3D continuously operated fluidized beds

传统的流化床放大理论大多基于流体力学相似性[48-51]，一般需要通过直接法[52]（测量气泡特性参数、最小流化速度、床层膨胀率以及高速摄像、视频分析、电容和光学探测等）或间接法[53-55]（压力波动测量）两种实验手段对不同尺寸流化床流体力学相似性进行验证。为此，有些学者提出了包含多种无量纲参数的相似性放大规则，其中最为经典的是Glicksman 等[56-57]和Horio 等[58]的放大规则。但这些规则一般基于一些假设，如忽略颗粒间相互作用力以及化学反应和传热效应，同时要求颗粒大小、最小流化速度、气速等物性随流化床尺寸同步改变，并不适用于单独改变流化床尺寸的放大方式。本文所模拟的四个不同的三维连续进出料流化床如图1 所示，长度Lb分别为0.07、0.15、0.31、0.63 m，宽度和高度分别为0.06、0.5 m。

为验证模型的可靠性，采用赵虎[59]得到的长为0.15 m流化床的实验结果进行验证。实验所测颗粒粒度分布如图2 所示。Volk 等[60]发现，从破碎气泡、减少气体短路和增强气固接触效率的角度来讲，宽筛分颗粒要比单一粒径颗粒更好。因此，为获取不同粒径颗粒停留时间信息，同时加快计算速度，在实际CFD-DEM 模拟中将此连续分布离散为三种粒径。首先在连续粒径分布上取出有限个离散点，求出低阶矩[61]，然后使用P-D（product-difference）算法求解得到代表粒径及其权重（质量分数）[62]，离散结果如表1所示。

表2 总结了模拟参数，其中颗粒球形度是根据实验测得的最小流化速度结合Hua等[33]、Wen等[63]的研究，由式（30）、式（31）估算得到，DEM 模型中涉及的碰撞参数均设置为经验值。为获得足够的尺度信息，网格尺寸要足够精细[64-66]，因此选用规则的六面体网格，尺寸设置为5 mm，约为最大真实颗粒直径的8 倍。对于Geldart B 类颗粒，该网格大小足以获得与网格无关的模拟结果[67]。

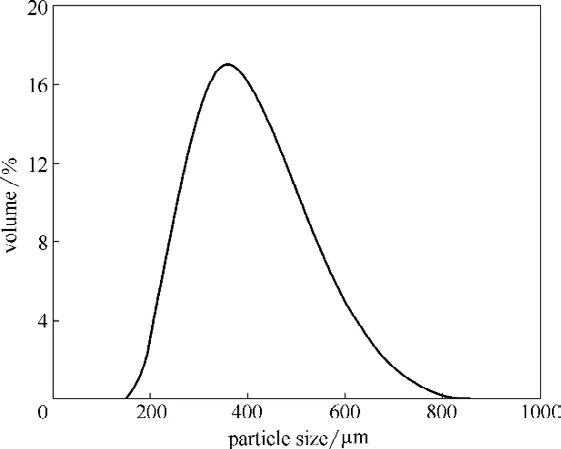
图2 实验所用颗粒尺寸分布Fig.2 Particle size distribution used in experiment

表1 模拟所用颗粒代表粒径及其质量分数Table 1 Representative particle sizes and their mass fractions used in simulations

3 结果与讨论

3.1 床层压力分布

不同尺寸流化床压力时均值轴向分布曲线如图3所示。可以看出0.15 m 流化床模拟结果和实验数据吻合较好，床内某一高度的压力随着流化床长度的增加变化不大，特别是0.31 m 与0.63 m 流化床床层压降曲线几乎重合，这是因为当流化床高度不变时，长度的增加对压降的影响很小。

表2 模拟参数和气体、颗粒物性Table 2 Simulation parameters for fluidized bed and properties of gas and particles

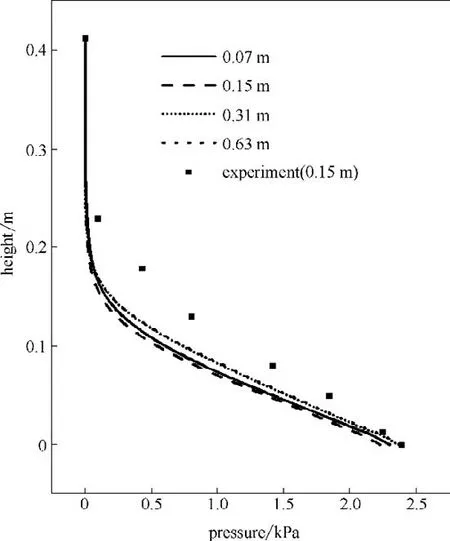
图3 不同长度流化床压力轴向分布Fig.3 Axial pressure distribution of fluidized beds with different lengths

表3为预测的不同大小流化床的平均存料量和全床时均压降，从表中可以看出，0.15 m流化床全床压降模拟结果与实验结果相对误差约为6.7%，说明所提出的非球形颗粒曳力模型能够较为准确地预测床内流动特性。另外系统流动稳定后平均存料量随流化床尺寸的增加而增大，并呈线性关系。全床压降随流化床长度的增加变化不大，这与图3 轴向压力分布的结果一致。

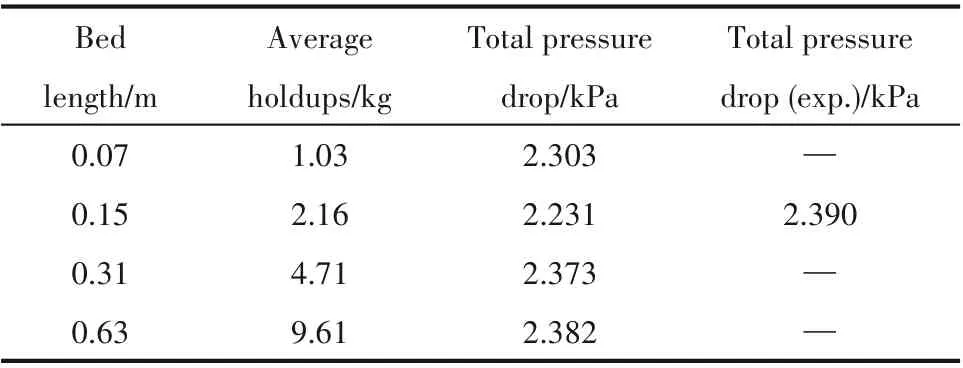
表3 不同尺寸流化床全床压降Table 3 Total pressure drop of fluidized beds with different sizes

3.2 固相浓度分布

图4 为1000 s 时不同尺寸流化床中心竖直截面处固相浓度分布情况。可以看出随着流化床长度的增加，气泡数量增多，直径变大。0.15、0.31、0.63 m 流化床床层膨胀高度基本一致，而最小床床层膨胀最高，这是由于壁面效应在较小尺寸流化床中更为明显[68]。床径较小时，床内气泡以节涌的形式向上移动，形成较大的气栓；而当床径较大时，气泡由于聚并而增大，上升速度加快，到达床层表面时发生破碎，气泡停留时间减短，气固接触效率降低。

图5给出了流化床内不同水平截面处固相浓度时均值的径向分布。从图中可以看出，沿床层径向，中心区固含率较壁面附近小，颗粒浓度呈现出中心稀、边壁浓的基本流动规律。沿床层轴向，颗粒浓度显示出上稀下浓的现象，床层下部区域由于气泡的存在，颗粒浓度径向变化更为剧烈，床层中、上部由于气泡的破碎，固相浓度分布更加均匀。随着流化床长度的增加，由于气泡数量的增多，床层下部固含率波动变大。

3.3 固相速度分布

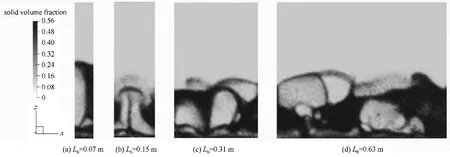
图4 t=1000 s时不同尺寸流化床中心竖直截面处固相浓度分布Fig.4 Contour of solid volume fraction at t=1000 s in central vertical plane for fluidized beds with different scale

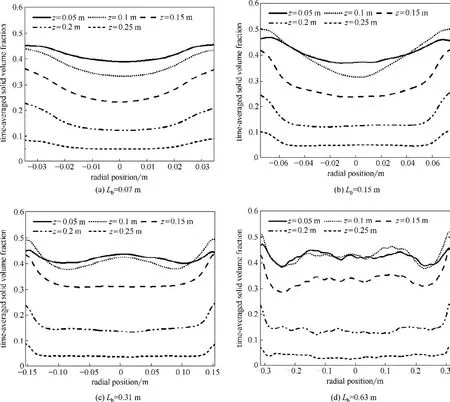
图5 不同尺寸流化床的固相浓度径向分布Fig.5 Radial distribution of solid volume fraction in fluidized beds with different scale

图6是流化床内不同水平截面处颗粒速度时均值的径向分布。从图中可以看出，当流化床床层高度小于（等于）0.15 m 时，长度为0.07 m 和0.15 m 的流化床床层中心区颗粒向上运动，边壁区颗粒向下运动，并且边壁区较宽；而对于长度为0.31 m 和0.63 m 的流化床，在较窄的边壁区，颗粒向下运动，在中心区与边壁区之间有速度波峰出现，在中心区部分颗粒被气泡夹带而向上运动，在气泡两侧及下部颗粒向下流动。当流化床高度大于（等于）0.2 m时，四个不同尺寸流化床内所有颗粒均向下流动，这是因为在床层上部气泡破碎，颗粒只在重力的作用下自由下落，而当接近床层表面（z=0.25 m）时，速度径向分布则变得较为均匀。

图6 不同尺寸流化床的固相速度径向分布Fig.6 Radial distribution of solid velocity in fluidized beds with different scale

3.4 颗粒停留时间分布

实验中采用脉冲法统计颗粒停留时间分布时，需要将示踪剂在很短的时间内从流化床入口注入系统。而在CFD-DEM 模拟中，颗粒本身充当示踪剂，由于入口处要以给定的速度生成颗粒，因此在很短的时间内如果在入口插入大量颗粒将会改变颗粒的进料速率。此外，一次性生成太多颗粒也会对流化床的流体力学行为产生很大影响。因此，在实际模拟中，当系统运行达到稳态后，把在一定时间间隔（150 s）内从入口生成的颗粒标记为示踪颗粒，然后监控这些颗粒的运动与停留时间，将其用于颗粒RTD的分析。

图7 是不同大小流化床内颗粒停留时间分布，E(t)为停留时间分布密度函数(s-1)，采用式（32）计算。

式中，mtracer,i为30 s 内从出口流出的示踪颗粒i的质量;n 为流出示踪颗粒数量;mtracer为该时间间隔内进入系统的示踪颗粒总质量。可以看出，四个不同尺寸的流化床颗粒RTD 出峰都很早，出现长拖尾现象，流动向全混流靠近，反映出典型的鼓泡流化床所具有的RTD特征[23]。在其他条件保持不变的情况下，随着流化床长度的增加，颗粒RTD 峰值降低，分布变宽。一方面由于床内细颗粒返混严重[20,39]，另一方面粗颗粒所受气体曳力较小，从而导致停留时间更长，曲线长拖尾明显。这意味着颗粒逆流严重而不能及时流出系统，对于含有化学反应的多分散流动系统，可能会造成粗颗粒过度反应而细颗粒转化不完全，从而降低反应效率。此外，通过与实验数据[图7（b）]的对比，发现所提出的Di Felice-Ganser曳力模型很好地预测了0.15 m流化床的颗粒RTD。实验中第一个数据点出现异常，这是因为流动稳定后大量示踪剂的注入引起床层波动所致，而在模拟中所采用的示踪颗粒进料方式并不会给颗粒整体的流动带来任何影响。从RTD 曲线的光滑程度来看，流化床越大，曲线噪声越多，这是因为较大的流化床示踪颗粒数量不足，即在流化床尺寸放大的同时，示踪颗粒的质量（数量）同样需要“放大”。在之前的研究中发现[34]，示踪颗粒进料时间间隔越长，示踪颗粒数量越多（即用于计算停留时间分布密度函数的颗粒样本数越多），RTD 曲线越光滑，但在一定时间段内，示踪颗粒数量对曲线的峰值、宽度以及颗粒平均停留时间几乎没有影响。因此，如有必要可以通过标记更多的示踪颗粒来减少较大流化床颗粒RTD曲线的噪声。

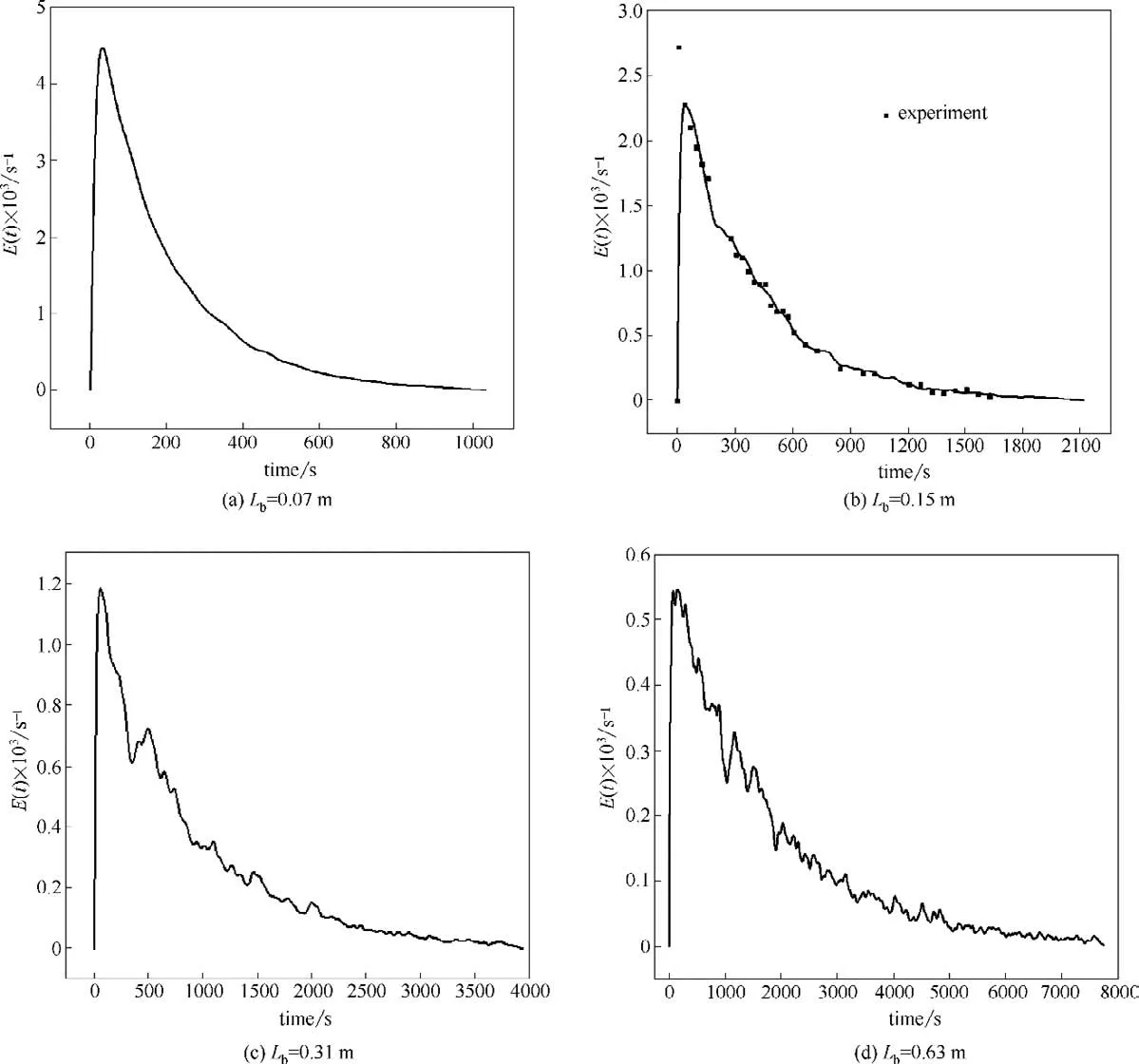
图7 不同尺寸流化床颗粒停留时间分布Fig.7 Particle RTD of fluidized beds with different scale

3.5 平均停留时间

表4列出了流化床放大时颗粒平均停留时间的模拟结果。本文中平均停留时间tm采用式（33）计算。

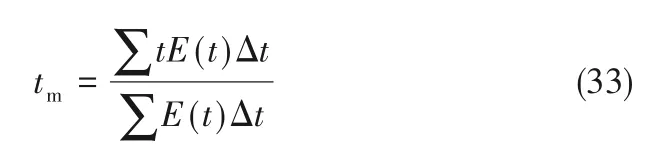
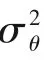
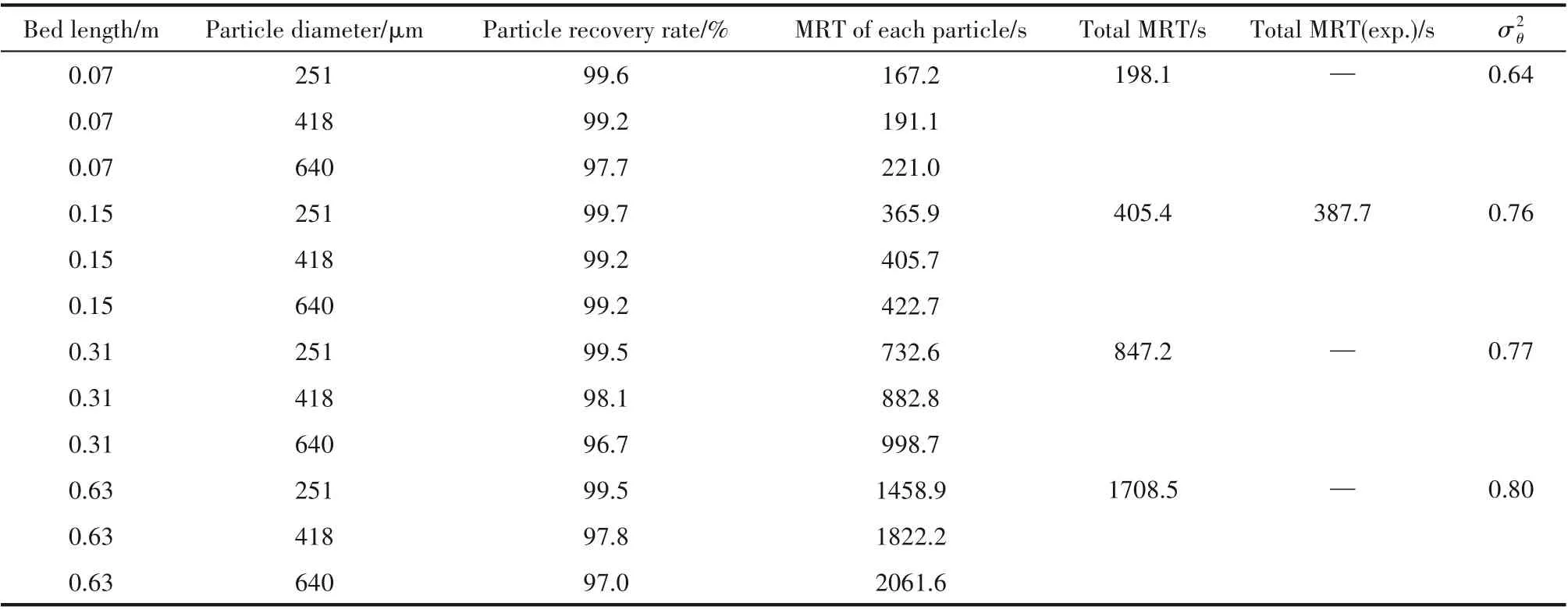
表4 不同尺寸流化床颗粒平均停留时间Table 4 Particle MRT of fluidized beds with different scale

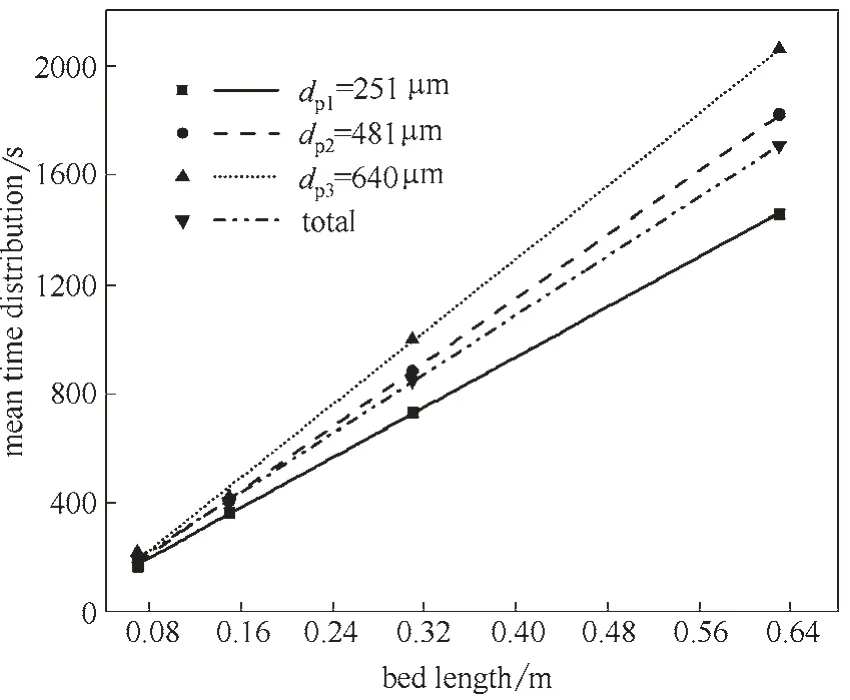
图8 不同粒径颗粒MRT与流化床长度的关系Fig.8 Relationship between MRT of particles with different sizes and bed length

为进一步发现放大过程中不同尺寸流化床颗粒MRT 之间的关系，图8 给出了宽筛分系统每种颗粒以及所有颗粒MRT 随流化床长度的变化曲线。从图中可以看出，无论每种颗粒还是所有颗粒，其平均停留时间与流化床长度均表现出线性关系，这是由于固体颗粒进料速率保持不变，颗粒横向平均速度也基本不发生改变，系统内每种颗粒以及所有颗粒平均停留时间便随流化床长度线性增加。可以利用这个结果来预测更大尺寸同类型流化床颗粒的平均停留时间。另外可以看到，流化床越长，不同粒径颗粒MRT 的差异越大，说明流化床长度的变化对颗粒停留时间也起到了一定的调控作用。