预测天然气斜井临界携液流量新方法
2022-08-18王月杰张宏友
王月杰 张宏友
中海石油(中国)有限公司天津分公司
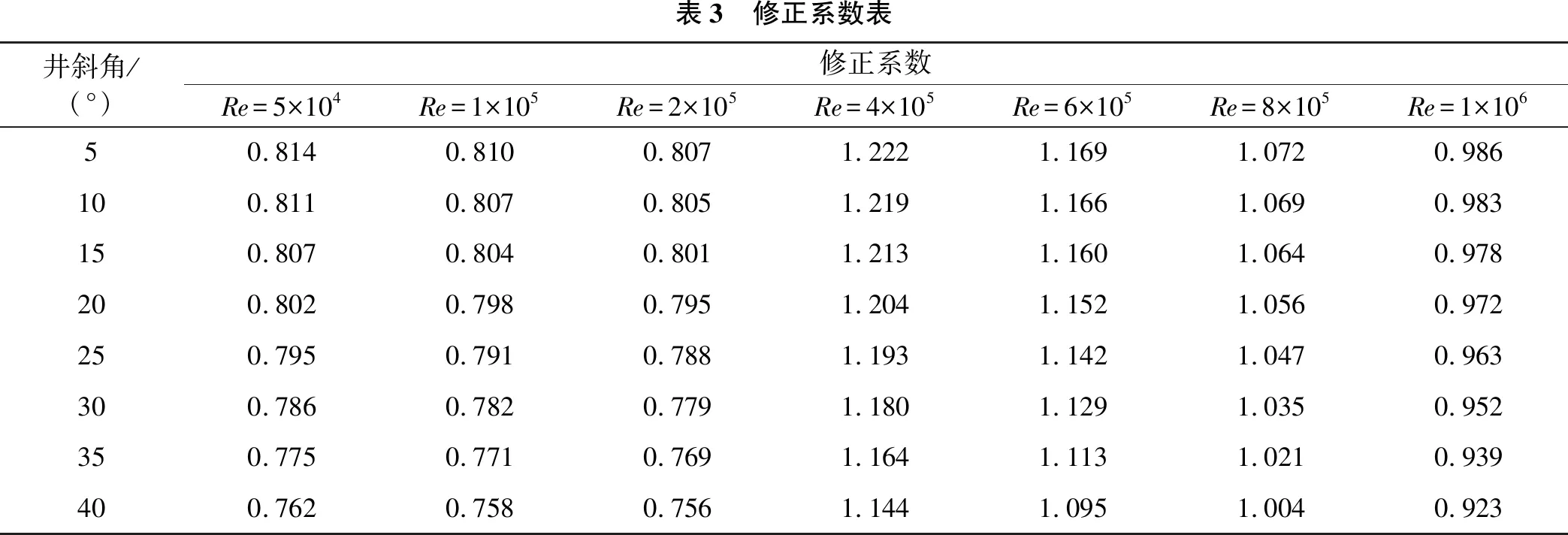
在气田开发过程中,井底积液是最常见的问题之一。积液会导致气井产量下降,甚至会造成气井停产,临界携液流量的准确计算对于判断气井积液十分重要[1-3]。Turner模型[4]和李闽模型[5]在现场比较常用,二者均是直井携液模型,将曳力系数取为0.44。杨文明等[6]分析了天然气斜井中液滴的受力情况,假设液滴沿井筒方向运动,不与管壁发生摩擦,这在斜井的实际生产中显然是不合理的。李丽等[7]以Turner模型为基础,考虑井斜角的影响,建立了斜井携液模型,但该模型未考虑曳力系数变化对临界携液流量的影响。Turner假设气井中液滴的雷诺数(Re)范围为104 在天然气斜井中,液滴受力如图1所示。根据液滴质点受力分析可知,如果液滴在井筒中间运动,液滴会受到曳力、浮力和重力3个力作用,由于液滴所受浮力和重力是沿垂直方向的,而曳力是沿井筒方向的,故液滴在这3个力作用下无法平衡。曳力垂直分力、浮力和重力在垂直方向上达到平衡,液滴在曳力水平分力的作用下,不断地在水平方向上向井口运动,直至靠近气井管壁位置,进而沿着气井管壁发生滑动。当天然气斜井中的液滴与气井管壁发生接触后,将受到曳力、浮力、重力、支撑力和摩擦力的作用。 根据牛顿第二定律,当达到临界状态时,天然气斜井中液滴受力达到平衡,会沿着气井管壁匀速移动,此时液滴沿井筒方向的受力关系如式(1)所示。 FD+(Fb-Fg)cosα-Fτ=0 (1) 式中:FD为曳力,N;Fb为浮力,N;Fg为重力,N;Fτ为摩擦力,N;α为井斜角,(°)。 液滴受到的曳力FD、浮力Fb与重力Fg计算公式如式(2)所示。 (2) 式中:d为液滴直径,m;ρG为气体密度,kg/m3;ρL为液滴密度,kg/m3;v为气流速,m/s;CD为曳力系数;g为重力加速度,m/s2。 液滴所受气井管壁的摩擦力遵循牛顿内摩擦定律,在管壁处流体切应力τ如式(3)所示。 (3) 式中:τ为管壁处流体切应力,Pa;Δp为液体流经长度为l的管道压力损失,Pa;r为管道半径,m;Re为液滴雷诺数。 结合式(3),可得液滴所受摩擦力Fτ,如式(4)所示。 (4) 当气流能把直径最大的液滴带出井口时,气井可以连续携液,井筒就不会积液[14]。气井中液滴的最大直径是由韦伯数决定的,一般来说,气井中液滴的临界韦伯数为20~30。前人研究表明[15],当液滴的韦伯数超过临界值时,液滴就会发生破碎。所以,气井中液滴最大直径可由式(5)计算得出。 (5) 式中:σ为气液界面张力,N/m。 将式(2)、式(4)和式(5)代入式(1),可得临界携液流速,如式(6)所示。 (6) 临界携液流量公式如式(7)所示。 (7) 式中:qc为临界携液流量,m3/d;A为油管截面积,m2;Z为气体偏差因子;T为温度,K;p为压力,MPa。 将式(6)变换为式(8),即本研究新模型。 (8) 式中:C为修正系数, 括号内为Turner模型计算结果。 理论和实验研究表明,在不可压缩流体中,光滑球体的曳力系数是雷诺数的函数。前人已经研究出很多用于计算光滑圆球曳力系数的公式,其中应用较为广泛的曳力系数计算模型如表1所列。 表1 曳力系数计算模型总结研究者模型适用范围公式序号邵明望[16]CD=24Re+3.409 Re-0.308 3+3.68×10-5Re1+4.5×10-5Re1.054Re <2×105式(9)Brauer[17]CD=24Re+0.4+4Re0.5Re <2×105式(10)Clift[18]CD=24Re(1+0.152 Re0.677)+0.4171+5 070 Re-0.94Re <2×105式(11)Ceylan[19]CD=1-0.5 e0.182+10.11Re-2/3e0.952Re-1/4-0.038 59Re-4/3e1.30Re-1/2+ 0.037×10-4Re e-0.125×10-4Re-0.116×10-10Re2 e-0.444×10-5ReRe <106式(12)Morrison[20]CD=24Re+2.6 (Re/5)1+(Re/5)1.52+0.411(Re/263 000)-7.941+(Re/263 000)-8.00+Re0.8461 000Re <106式(13)Barati[10] CD=8×10-6[(Re/6530)2+tanh(Re)-8ln(Re)/ln(10)]-0.4119 e-2.08×1043/[Re+Re2]4+2.134 4 e-{[ln(Re2+10.756 3)/ln(10)]2+9.986 7}/Re+0.135 7e-[(Re/1620)2+10 370]/Re-8.5×10-3{2ln[tanh(tanh(Re))]/ln(10)-2 825.716 2}/Re+2.479 5Re <106式(14) 为了评估表1中各曳力系数计算模型的精确度,引入对数偏差平方和(SSLD)、对数偏差均方根(RMSLD)与相对误差和(SRE),如式(15)~式(17)所示。 (15) (16) (17) 采用文献[21, 22]中的实验数据将各曳力系数计算模型进行了对比,结果见表2和图2 。 由表2可知,一些模型具有较大的 SSLD 、RMSLD和SRE值(即低精度),如Brauer模型、邵明望模型和Clift模型。这是因为这些模型的适用范围为Re<2×105,作为拟合关系式,它们没有拟合2×105 表2 不同曳力系数计算模型精确度比较精确度排序模型SSLDRMSLDSRE1Barati0.009 70.026 40.516 32Morrison0.049 80.059 70.972 83Ceylan0.061 60.066 41.216 24Brauer1.208 20.293 810.845 85邵明望1.427 30.319 312.429 06Clift1.474 50.324 512.793 8 由式(8)可知,修正系数由井斜角、雷诺数和曳力系数决定,而曳力系数是雷诺数的函数。图3为井斜角和雷诺数对修正系数的影响。由图3可知,随着井斜角的增大,修正系数逐渐减小,与之对应的临界携液流量也相应减小。当104 表3 修正系数表井斜角/(°)修正系数Re=5×104Re=1×105Re=2×105Re=4×105Re=6×105Re=8×105Re=1×10650.8140.8100.8071.2221.1691.0720.986100.8110.8070.8051.2191.1661.0690.983150.8070.8040.8011.2131.1601.0640.978200.8020.7980.7951.2041.1521.0560.972250.7950.7910.7881.1931.1421.0470.963300.7860.7820.7791.1801.1291.0350.952350.7750.7710.7691.1641.1131.0210.939400.7620.7580.7561.1441.0951.0040.923 续表3井斜角/(°)修正系数Re=5×104Re=1×105Re=2×105Re=4×105Re=6×105Re=8×105Re=1×106450.7470.7430.7411.1221.0730.9840.905500.7290.7260.7231.0951.0480.9610.884550.7090.7050.7031.0651.0180.9340.859600.6850.6820.6791.0290.9840.9020.830650.6570.6540.6510.9860.9430.8650.796700.6230.6200.6180.9350.8950.8200.755750.5810.5780.5760.8720.8350.7650.704800.5260.5230.5220.7900.7550.6930.637850.4430.4400.4390.6650.6360.5830.536 基于文献[23]中的37口积液气井数据,分别采用本研究模型和几种常用的斜井携液模型计算天然气斜井临界携液流速,结果见图4。假设气井气流速等于其临界携液流速,对角线为基准线,则积液气井临界携液流速计算值应处于对角线的上方。由图4可知,杨文明模型计算结果明显偏小[6],Belfroid模型预测准确率仅为24.3%[24],李丽模型预测准确率为45.9%[7],而本研究模型仅误判2口井,准确率为94.6%。 采用本研究模型和几种常用的斜井携液模型对文献[7]中2口临近积液气井数据进行计算,计算结果见表4。由表4可知,本研究模型计算结果较几种常用斜井携液模型更为准确。 由图4和表4可知,本研究模型计算结果具有较高的精度,与气井实际情况吻合较好,从而验证了本研究天然气斜井携液模型的可靠性,可用于对天然气斜井积液的判断。 表4 不同模型计算结果对比表井名E1井E2井井斜角/(°)4045油管内径/mm6262产水量/(m3·d-1)3.22.5临界携液流量/(104 m3·d-1)2.603.20Belfroid模型计算值/(104 m3·d-1)2.172.75相对误差/%16.5414.06杨文明模型计算值/(104 m3·d-1)1.712.24相对误差/%34.2330.00李丽模型计算值/(104 m3·d-1)2.743.47相对误差/%5.388.44本研究模型计算值/(104 m3·d-1)2.663.34相对误差/%2.314.37 (1) 对天然气斜井中的液滴进行受力分析,认为液滴最终沿气井管壁发生滑动。 (2) 考虑曳力系数变化对临界携液流量的影响,采用实验数据对比不同曳力系数计算模型的精确度,优选出Barati模型计算气井中液滴的曳力系数。 (3) 考虑井斜角和曳力系数,对Turner模型进行了修正,并给出了修正系数速查表。结合实例分析,本研究模型计算结果具有较高的精度,准确率为94.6%。1 模型建立
1.1 数学模型

1.2 曳力系数



1.3 修正系数


2 实例验证


3 结论
