基于随机森林的不可靠数据化工过程故障诊断方法

冯子芸， 王治红， 戴一阳

(1.西南石油大学 化学化工学院，四川 成都 610500；2.四川大学 化学工程学院，四川 成都 610065)

化工过程的故障诊断技术是化工过程在自动化程度与日俱增情况下，保障化工行业安全运行的一个重要手段。随着化工企业硬件条件的提升和大数据技术的高速发展，化工过程的数字化、智能化发展脚步日益加速，基于数据驱动的故障诊断方法也成为研究最广、应用前景最广泛的方法。利用大量的历史数据训练诊断模型，不仅能快速地检测出故障，更能有效识别故障类别，从而可以在实际操作中指导操作员做出正确响应。

传统的基于多元统计和降维的方法，如：偏最小二乘法(Partial Least Squares，PLS)[1]和主成分分析法(Principal Component Analysis，PCA)[2]等，在故障检测的研究中表现出了良好的性能，但在故障类型的识别上表现不尽如人意。而一些基于模式识别的机器学习方法在故障检测和故障识别领域都有较好的表现，如：支持向量机(Support Vector Machine，SVM)[3]、k最小近邻(k-Nearest Neighbors，kNN)[4]、贝叶斯网络(Bayesian Network，BN)[5]和人工神经网络(Artificial Neural Networks，ANN)[6]等。随着深度学习的不断发展，深度信念网络[7](Deep Belief Network，DBN)和卷积神经网络(Convolutional Neural Networks，CNN)[8]方法在大数据条件下的故障诊断中表现出了优异的能力。

然而，化工过程现场采集到的监测数据，常因传感器故障、传输路线损坏及仪器量程溢出等原因而失真，出现数据的缺失、漂移或卡死等问题，影响故障诊断方法的准确性。因此，对存在不可靠数据的化工过程进行故障诊断研究具有重要意义。

基于数据不完整情况下的故障诊断已有不少报道。Liu等[9]针对数据不完整的热泵故障系统，提出了一种基于反向传播神经网络(Back Propagation Neural Network，BPNN)和最大似然估计(Maximum Likelihood Estimation，MLE)的方法，对不完整的数据集进行估算，再利用BN建立分类器模型，完成故障类型的识别。Askarian等[10]采用了ANN、KNN、均值法等方法完成对缺失数据集的修补，再与不同的分类方法进行组合，最后通过鲁棒性和准确性等指标对采用不同组合方法故障诊断结果进行评价。然而，先估算不可靠数据再进行故障诊断的两步方法，在实际应用过程中可能会出现时间滞后，影响故障的及时诊断和处置。同时，在实际过程中，监测数据不仅存在缺失的现象，同时还存在漂移、卡死、噪声等其他异常情况。监测数据的异常情况通常更难发现，导致无法高效识别故障类型。

随机森林(RF)方法具有分类精度高和泛化能力强的特点，对噪声和异常值的稳健性较好。该方法在数字识别、图像处理和数据挖掘等众多领域受到广泛关注[11-13]。笔者针对田纳西-伊斯曼过程(Tennessee Eastman，TE)数据缺失、漂移和卡死3种不可靠情况，提出将随机森林方法用于不可靠数据的化工过程故障诊断研究，并将该方法与反向传播神经网络(BPNN)、径向基函数神经网络(Radial Basis Function Neural Network，RBFNN)和深度信念网络(DBN)方法进行比较，以考察基于随机森林的方法在处理存在不可靠数据的化工过程故障诊断中的表现。

1 随机森林理论

2001年，Breiman将自举汇聚法(Bagging)与Ho提出的随机子空间方法相结合，在Bagging的基础上引入了随机属性，提出了随机森林(RF)学习方法[14]，并阐述了RF的数学理论，证明了RF不会出现决策树的过拟合问题。在RF模型训练过程中随机选取样本和特征属性，从而能够提高模型的不确定性和多样性。具体如下：

(1)随机样本：从原样本集中有放回地随机抽取，得到K个训练样本集。未被抽取的数据叫做袋外数据(OOB, Out of bag)，用于检验决策树的分类效果。

(2)随机属性：从M个总特征中，等概率地随机选取m个特征(m通常取M的平方根)作为特征子集。

RF采用分类与回归树(CART)对K个训练样本集进行训练，以随机的方式构建K棵决策树。各决策树在相应的子集中选择一个最优属性作为分裂节点进行分裂，并按照最优分裂原则进行最大化生长，且各决策树的训练相互独立。最后采用投票法根据各决策树的预测结果得到最终输出的分类结果。

基于上述方法构建的随机森林中，每颗决策树的特征变量不完全相同。在分类投票时，即使部分变量不可靠也只会影响包含该特征变量的一部分决策树，不会影响其他树的分类结果，通过投票能够减小不可靠变量对最终分类结果的影响。鉴于此，本研究利用随机森林的投票机制，开发化工过程故障诊断模型，有望克服无关变量的干扰和数据不可靠对诊断结果的影响。RF算法的流程如图1所示。

图1 随机森林算法流程图Fig.1 Flowchart of the random forest algorithm

2 基于RF的TE过程故障诊断方法

田纳西-伊斯曼(TE)过程是Downs和Vogel根据美国Eastman化学公司的实际化工反应过程开发的仿真平台[15]。该过程被广泛应用于故障诊断方法的性能测试，成为评价诊断方法的一个标杆。基于RF的故障诊断方法以TE过程为研究对象，测试其诊断存在不可靠数据的化工过程故障的能力。其诊断框架如图2所示。

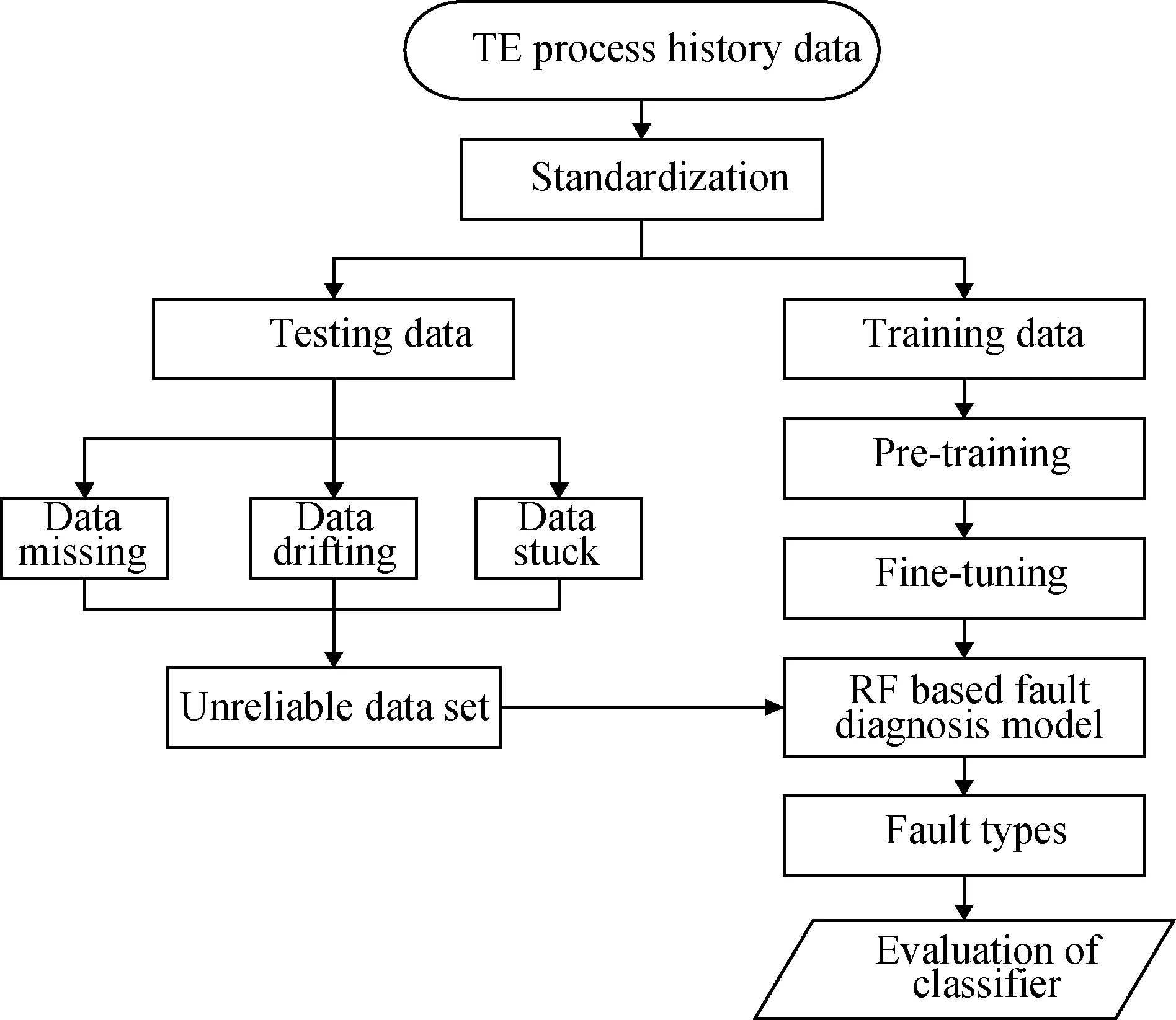
图2 基于随机森林的故障诊断框架Fig.2 The framework of fault diagnosis based on RF

基于RF的TE过程故障诊断流程分为以下几个步骤：

(1)采集TE过程的原始故障数据，对其进行归一化预处理，并将处理后的数据分为：训练集和测试集，其中X和Y分别是变量特征和故障类型标签。

(2)将训练集输入随机森林网络进行训练，训练过程中不断调整网络，得到最优的RF分类器。即决策树的数量K为2500，随机属性的个数m为8。

(3)对TE过程的测试集进行数据缺失、数据漂移和数据卡死的处理，得到本研究所需要的不可靠数据集。

(4)将存在数据不可靠的测试集输入训练好的RF分类器进行故障诊断。采用相对多数投票原则，由各决策树投票数量确定最终分类结果，分类公式为：

(1)

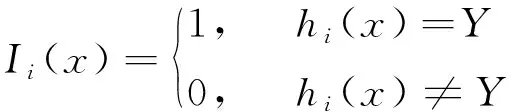
(2)

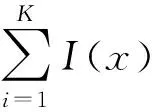
(5)采用故障诊断率(Fault Diagnosis Rate,FDR)作为故障诊断的分类评价指标，对诊断结果进行分析。

(3)

式(3)中：T(True)和P(Positive)分别表示真实、正类；TP为真正类，表示样本的真实类别是正类，并且预测类别也为正类；FP为假正类，表示样本的真实类别是负类，但预测类别为正类； TP和FP可由混淆矩阵[16]得到。

测试数据来自于MIT的BraatzGroup实验室的标准样本集。该样本集包括52个变量及21种预先设定的故障类型。每种故障的训练数据来自故障状态下仿真24 h产生480组样本数据；其测试数据来自过程正常运行8 h后引入相应故障而得到960组数据，其中前160组为正常状况下的数据，后800组样本为对应故障的数据。将52个变量作为RF分类器的输入，故障类型作为输出。

对测试样本进行数据不可靠处理，分别得到数据缺失、数据漂移和数据卡死3种情况下的测试集。以反应原料D的进料流量为例，对第100个采样点后的数据进行数据缺失、数据漂移和数据卡死处理，并经过归一化处理后得到如图3所示的监测变量数据集。

3 诊断结果分析

针对TE过程数据缺失、漂移和卡死3种不可靠情况，采用基于RF的故障诊断方法进行故障分析测试，并以FDR为指标与采用BPNN、RBFNN和DBN方法诊断进行性能比较。

3.1 数据缺失

化工过程的监测数据往往存在缺失的现象，使得故障诊断模型的输入不完整，严重影响故障诊断的准确性。研究在监测数据完整、单变量数据缺失、多变量数据缺失和随机变量数据缺失等多种情况下，分析不同故障诊断方法的诊断效果。

3.1.1 数据完整和单变量数据缺失

在TE过程的52个变量数据完整和单一变量数据缺失2种情况下，采用RF、BPNN、RBFNN、DBN诊断方法的平均诊断率如图4所示。由图4可知，在数据完整情况下，RF方法的平均诊断率超过70%，DBN、BPNN、RBFNN方法的平均诊断率依次下降。当存在单变量数据缺失的情况时，RF方法的诊断率波动最小，诊断效果最好，其中当变量21、45、46和51缺失时，RF方法的平均诊断率有较明显的下降趋势；BPNN和DBN方法仅个别变量数据缺失时的诊断率保持稳定，多数单一变量数据缺失时诊断率波动很大；RBFNN方法的诊断波动最大、效果最差。

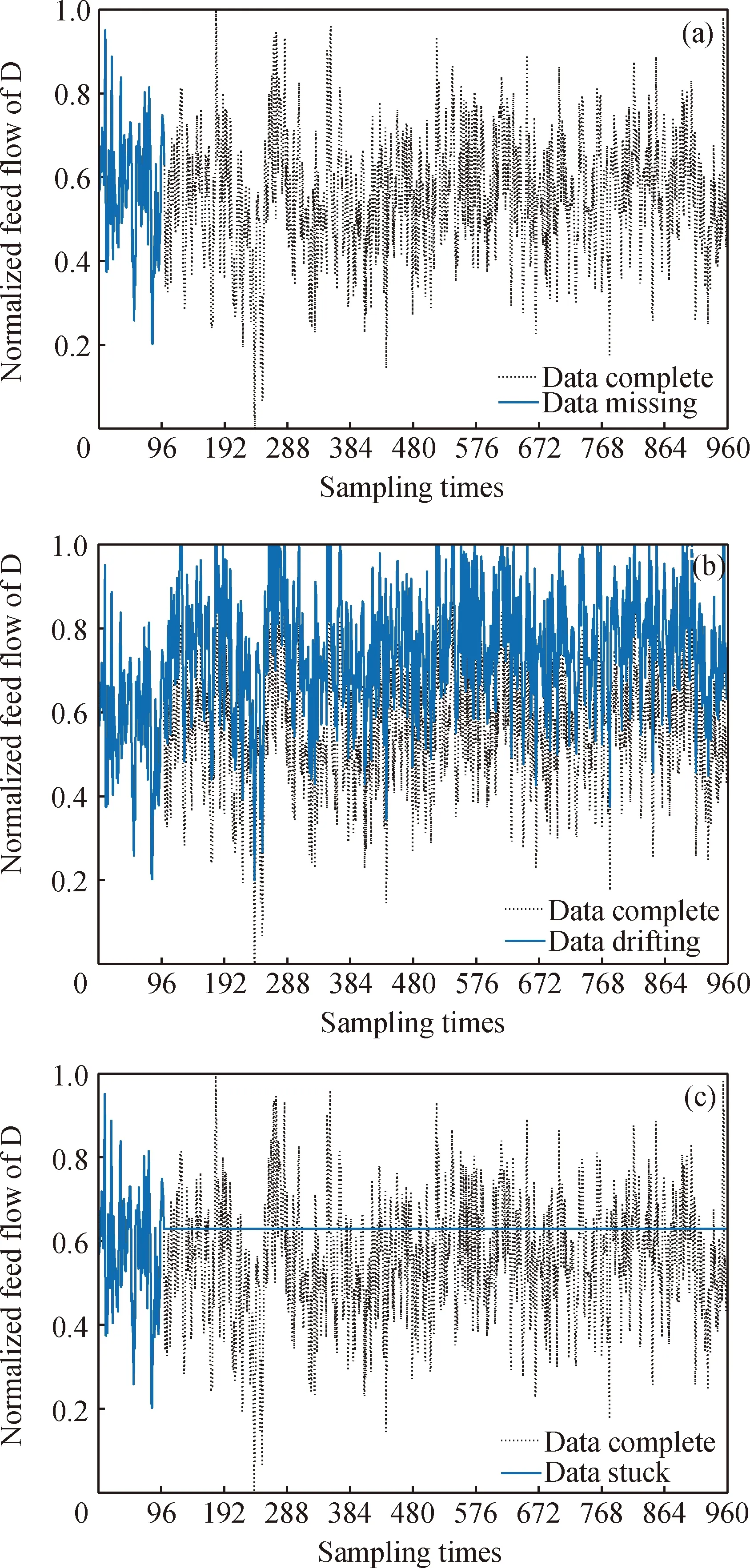
图3 D进料流量的不可靠数据集Fig.3 Unreliable data set of D feed flow(a) Data missing; (b) Data drifting; (c) Data stuck

3.1.2 多变量数据缺失

针对多个变量数据同时缺失情况，如2个或3个变量数据同时缺失时，考察不同诊断方法的诊断效果。

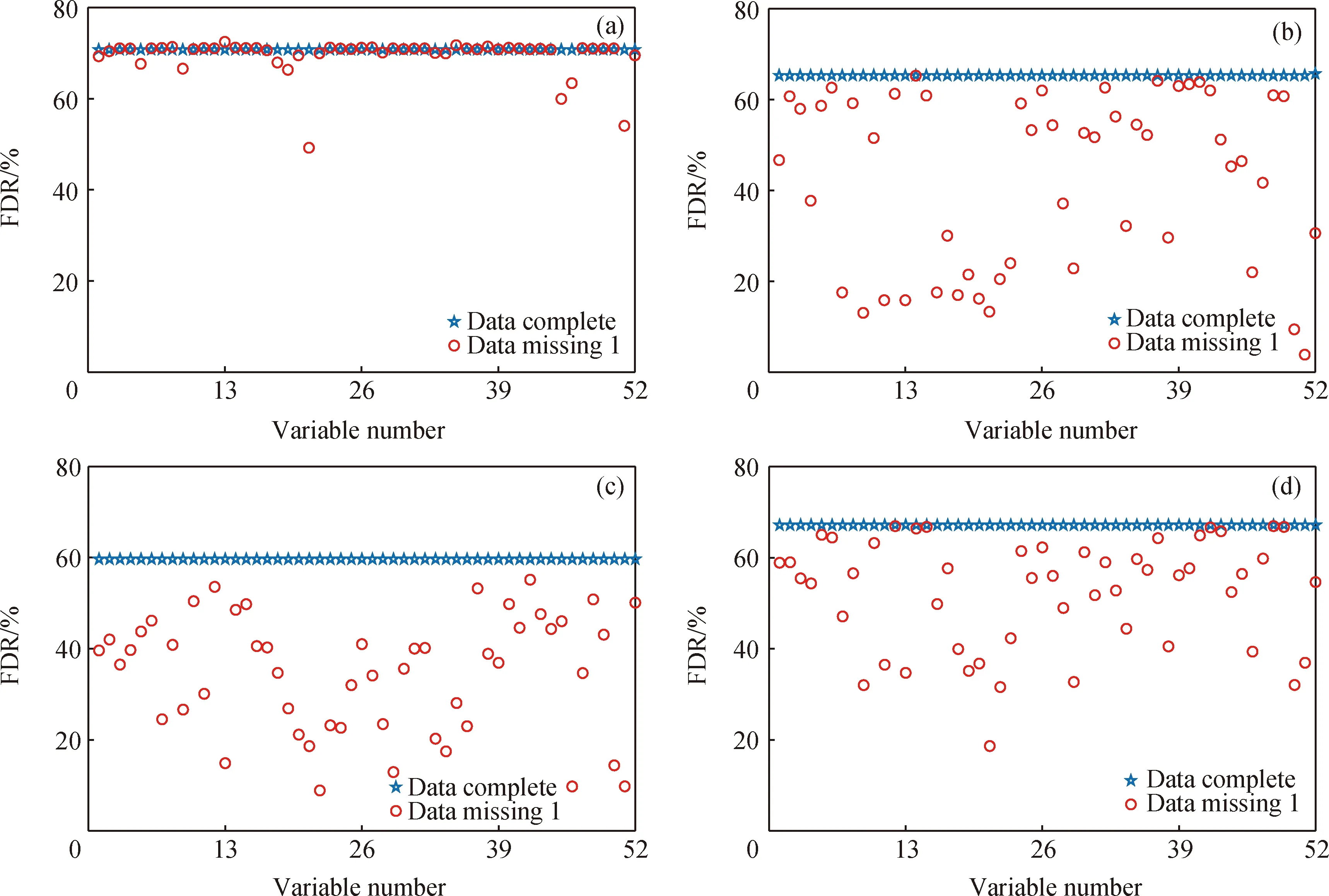
图4 单一变量数据缺失时不同诊断方法的诊断率(FDR)Fig.4 FDR of different methods at univariate missing(a) RF; (b) BPNN; (c) RBFNN; (d) DBN

对于2个变量同时缺失的情况，以变量1与k(其他51个变量之一)同时数据缺失为例，不同诊断方法的诊断结果如图5所示。由图5可知：当2个变量数据同时缺失时，RF方法的平均诊断率整体上低于数据完整和单变量数据缺失的诊断率，但诊断基本处于稳定状态，表明随机森林方法具有良好的稳健性和泛化性；采用BPNN、RBFNN、DBN方法对相同数据集进行分类诊断，其诊断结果波动剧烈，且整体上大幅低于数据完整时的诊断率。因此，当2个变量数据同时缺失时，RF的诊断效果明显优于其他诊断方法。

由于单变量数据缺失和双变量数据缺失时，各方法诊断结果的趋势相同，针对3个变量数据同时缺失的情况，仅讨论RF方法的诊断结果。当变量1、2与k(其他50个变量之一)数据同时缺失时，RF方法的故障诊断结果如图6所示。由图6可知，当3个变量数据同时缺失时，RF方法的诊断结果依然能够保持较好的稳定性。

上述结果表明，RF方法无论在单变量、双变量或三变量数据缺失时都能够有效地识别故障类型。RF方法在不同个数变量数据缺失时(类型I—数据完整；类型II—单一变量数据缺失；类型III—2个变量数据缺失；类型IV—3个变量数据缺失)，各故障类型的诊断结果如表1所示。由表1可知，在单变量数据缺失情况下，各故障类型的平均诊断率仅比数据完整情况下的平均诊断率低1.28%；在2个或3个变量数据同时缺失时，其平均诊断率仍然高达67%。

3.1.3 变量数据随机缺失

对TE过程的测试样本数据，分别按5%、10%、15%和20%的比例进行随机变量数据缺失处理，获得相应的测试集，将新的测试集分别输入RF、BPNN、RBFNN和DBN诊断方法，诊断结果如图7所示。由图7可知：当数据完整时，RF、BPNN、DBN诊断方法的诊断率均超过60%；当缺失数据比例为5%时，BPNN方法的诊断率下降40%， DBN方法的诊断率下降20%，而RF方法的诊断率仅下降8%；随着缺失比例的增大，RF方法的诊断率的下降幅度较小，其余3种方法的诊断率下降幅度很大；当测试数据的缺失达到20%时，RF、DBN、RBFNN和BPNN方法的诊断率分别约为55%、30%、10%和10%，RF方法诊断效果最好。由上述结果显示可知，随着变量数据缺失比例增加，基于RF的诊断方法仍能保持较好的诊断效果。

图6 3个变量数据同时缺失时RF方法的诊断率Fig.6 FDR of RF at three variables missing

3.2 数据漂移

在化工过程数据的采集过程中，传感器会受到环境的影响，导致监测数据较真实值发生漂移，进而影响故障诊断结果。采用不同的诊断方法分别对监测变量数据存在正、负漂移的情况进行诊断分析，如图8和图9所示。由图8和图9可知，对于数据存在正、负漂移的情况，除个别变量外，多数变量数据的漂移对RF方法的故障诊断影响很小；DBN方法的诊断效果虽优于BPNN和RBFNN方法，但波动也很大。这说明RF方法具有较强的抗噪能力，在数据漂移时的诊断分析中具有较高的精确度。

表1 不同数据缺失情况下的诊断效果比较Table 1 Performance of different data missing

图7 不同数据缺失比例下不同诊断方法的平均诊断率Fig.7 Average FDR of different methods at differentdata missing ratios

3.3 变量数据卡死

针对监测变量数据卡死的情况，以TE测试样本的第100个监测点卡死为例，各变量数据分别卡死情况下，采用RF、BPNN、RBFNN、DBN方法诊断的结果如图10所示。由图10可知，变量数据卡死时，RF方法的诊断效果明显优于其他3种方法，其平均诊断率比数据完整情况下诊断率约低0.5%。当以RF作为分类方法时，仅在变量9、21、45、51数据卡死情况下，其诊断率有较明显的波动。DBN方法整体的诊断率的波动也比较小，但其在变量9、10、17、18、19、20、21、44、45、46、50、51、52数据卡死时的诊断效果有较明显的下降。因此，对于变量数据卡死情况，诊断效果最好的是RF方法，其次是DBN方法。

图8 变量数据正漂移时不同诊断方法的诊断率Fig.8 FDR of different methods at variable data positive drifting(a) RF; (b) BPNN; (c) RBFNN; (d) DBN

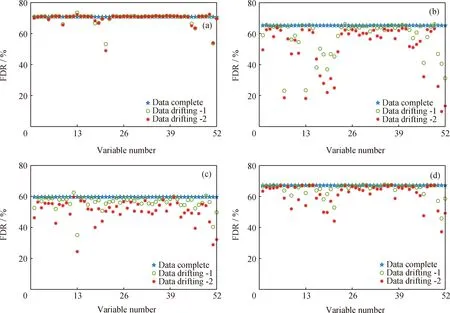
图9 变量数据负漂移时不同诊断方法的诊断率Fig.9 FDR of different methods at variable data negative drifting(a) RF; (b) BPNN; (c) RBFNN; (d) DBN

图10 变量数据卡死情况时不同诊断方法的诊断率Fig.10 FDR of different methods at variable data stuck(a) RF; (b) BPNN; (c) RBFNN; (d) DBN

4 结 论

针对TE过程数据缺失、漂移和卡死3种数据不可靠的情况，提出了基于RF的故障诊断方法。比较采用RF与BPNN、RBFNN、DBN方法对化工过程故障的诊断结果表明：在数据完整情况下，基于RF的故障诊断方法的故障诊断率最高；当数据存在不可靠的情况时，RF方法的故障识别受数据不可靠的干扰最小，诊断率波动最小，其他3种方法的诊断率明显下降，且波动很大；随着数据不可靠程度的上升，RF方法的故障诊断率下降速率较慢、波动较小，其他3种方法的诊断率下降速率较快，下降幅度很大，且波动明显。因此，基于RF的故障诊断方法分类精度高、泛化能力强、对不可靠的数据的容错能力较好。

基于RF的故障诊断方法对绝大多数变量的数据不可靠情况保持稳定的故障诊断率，但仍有少数变量数据不可靠会导致其诊断率有明显的下降。