管柱式气-液分离器溢流压力降计算模型

王亚安， 陈建义， 叶 松， 岳 题， 杨 洋， 韩明珊

(1.中国石油大学(北京) 重质油国家重点实验室， 北京 102249；2.过程流体过滤与分离技术北京市重点实验室，北京 102249)

管柱式气-液分离器(Gas-liquid cylindrical cyclone，简称GLCC)是油气生产系统中的关键设备，其结构紧凑、性能优越、运行稳定。其工作原理是：气、液两相首先在倾斜管中实现预分离，后沿切向进入主分离筒体。在主分离筒体内，受离心力与重力的双重作用，液相被甩至边壁向下运动，从底流口排出，气相则边旋转边向上，自溢流口流出，以此实现气、液分离。GLCC在运行时，伴随有2种特殊现象，即：气相携液现象及液相携气现象，在高气/液比情形下(一般认为入口体积含气率β≥95%)，气相携液现象是研究重点。然而，针对GLCC的气相携液现象，以往的研究多关注其分离效率，对压力降的研究还不够细致深入。事实上，与分离效率相同，压力降也是评价分离器分离性能的重要指标[1]，它不仅反映了设备的能耗水平，而且倘若掌握了其压力降的成因及组成，还可对分离器的优化设计提供支撑。因此，笔者关注高气/液比情形下的GLCC溢流压力降。

Arpandi等[2]为GLCC溢流压力降的研究奠定了基础，认为GLCC溢流压力降由3部分组成，即：气相摩阻压力降、气相重位压力降以及由于液相存在而造成的附加压力降。遗憾的是，Arpandi等未给出计算其阻力系数的表达式，而且忽略了气、液间的相互作用。董腾[3]将相似理论应用到GLCC的研究上，通过相似分析建立了基于相似准数的压力降预测模型。陈晓慧[4]则通过考虑介质物性，进一步完善了董腾的研究成果。此外，王婉琳[5]利用数值模拟的方法对GLCC的压力降进行了研究。最近，王亚安等[6]还将相似理论与人工神经网络相结

合预测了GLCC的溢流压力降值。研究者们虽获得了一定的研究成果，但所建立模型的理论性不强，且都不曾考虑流型分布、液滴携带等因素对GLCC压力降的影响。

事实上，经典的气-液两相流动理论认为[7]，压力降主要由3部分组成：摩阻压力降、重位压力降及加速压力降。在等截面绝热流动中，加速压力降可以忽略。此外，流体在经过局部阻力件(如弯管、阀门、法兰等)时会产生局部压力降。笔者基于气-液两相流动的基本理论，结合GLCC内部流动规律，建立了GLCC溢流压力降计算模型。

1 实验部分

1.1 GLCC实验装置及流程

GLCC实验装置尺寸如图1(a)所示。倾斜管内径d=54 mm，下倾角度θ=27°。入口采用矩形渐缩喷嘴，其与筒体相切，面积收缩比(即末端面积与始端面积之比)为0.74，末端长和宽分别为a=54 mm，b=40 mm。分离筒体的内径D=74 mm，筒体高/径比约为30。实验中沿程布置了4个测压点，利用JYB-3151压力传感器(北京昆仑海岸传感技术有限公司产品)实时测量，并利用RS485系统对气、液相流量及压力差信号实时在线采集。定义测点1和4之间的压力降为GLCC溢流压力降。GLCC实验流程如图1(b)所示。气相(空气)由高压风机鼓出，经涡街流量计测得体积流量Qg，实验范围为90～220 m3/h；液相(水)由泵增压后经涡轮流量计测得体积流量Ql，实验范围为0.6～3.0 m3/h。气、液两相经静态混合器混合后进入GLCC进行分离。分离后的气相从上部溢流口排出，再经立式丝网气-液分离器后，气相排入环境中；分离后的液相从下部底流口返回至水箱以循环利用。实验过程中，调节底流阀控制平衡液位的高度在入口以下约400 mm 处。

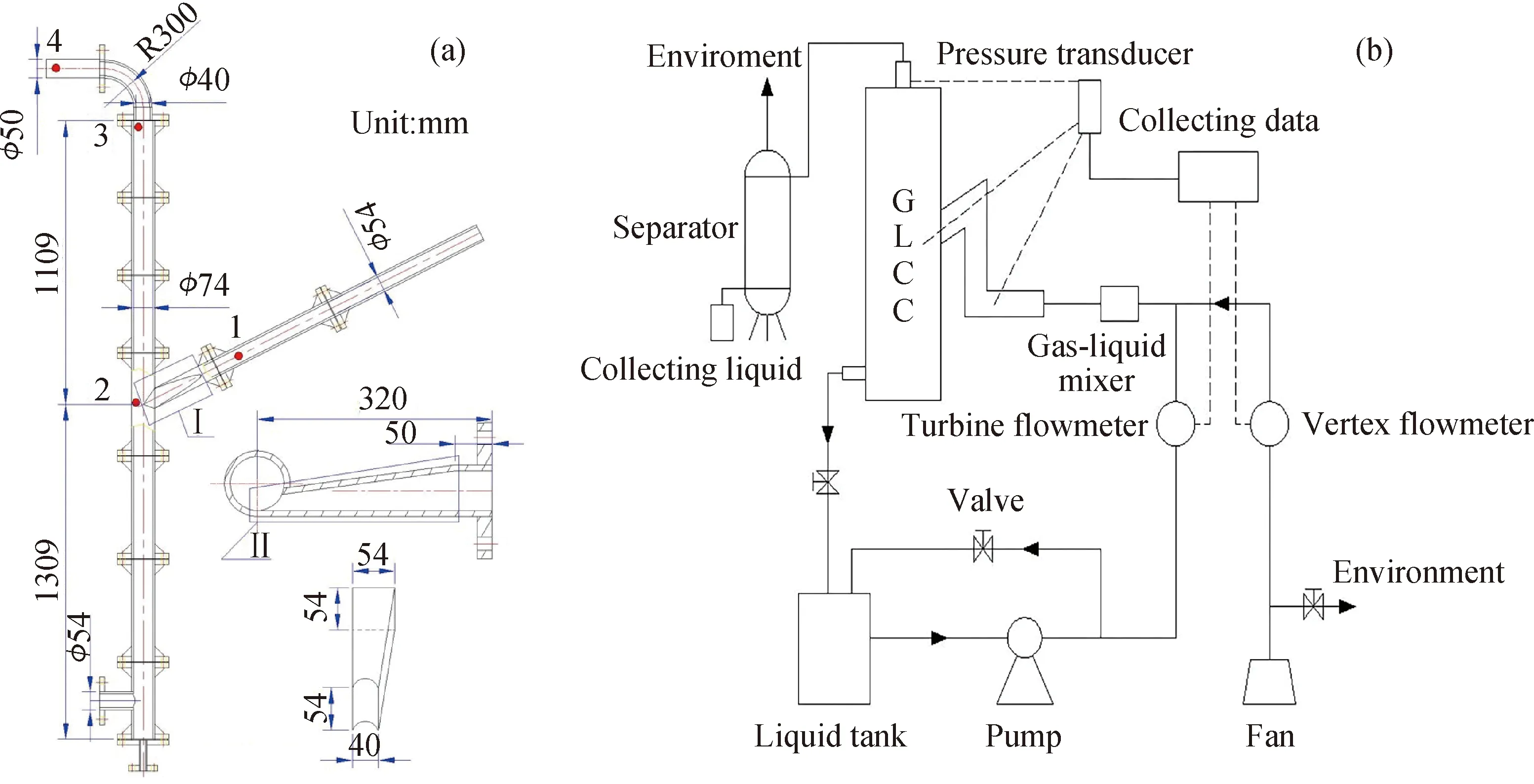
图1 GLCC实验装置及流程图Fig.1 Experimental device and flowchart of GLCC(a) Dimension of the tested GLCC； (b) Experimental flowchartNumbers 1, 2, 3， 4 represent the positions of pressure measurement point

1.2 不确定度评定

先对气、液相体积流量和溢流压力降的实验值进行不确定度评定，以某一工况(Ql=1.8 m3/h，Qg=190 m3/h)为例，参量的时域图如图2所示。参考不确定度评定方法[8]，在置信概率为95%的情况下，求得液体体积流量Ql的相对不确定度为3.29%；气体体积流量Qg的相对不确定度为2.45%；溢流压力降(Δp14)的相对不确定度为0.86%。基于此，认为实验数据准确可靠，可将数据用于模型分析。

图2 GLCC气、液体积流量和溢流压力降(Δp14)时域图Fig.2 Temporal data of gas flow-rate, liquid flow-rate and overflow pressure drop (Δp14) in GLCC(a) Gas, liquid flow-rate； (b) Overflow pressure drop (Δp14)

2 GLCC溢流压力降建模

根据GLCC的结构特征，笔者将其溢流压力降的组成分为3部分：入口(I区)压力降(Δp12)、筒体(II区)压力降(Δp23)和出口(III区)压力降(Δp34)。针对3个区间分别建模再加和，便可求出其总溢流压力降Δp14。为便于建模分析，特做以下假设：(a)流体无相变；(b)流体经过局部阻力件时截面含气率保持不变；(c)流体在倾斜管内呈现分层流流型。

2.1 入口(I区)压力降

GLCC入口管采用下倾角度θ=27°的矩形渐缩结构，并与筒体相切，该结构可使气、液相在倾斜管内实现分层并使流体进入主分离筒体时加速造旋。据其结构特点，可将入口压力损失拆分为渐缩损失和膨胀损失。

2.1.1 入口渐缩损失

图3为气-液两相在入口渐缩段内的流动示意图。流体自1-1断面流到2-2断面，其压力梯度可表示为：

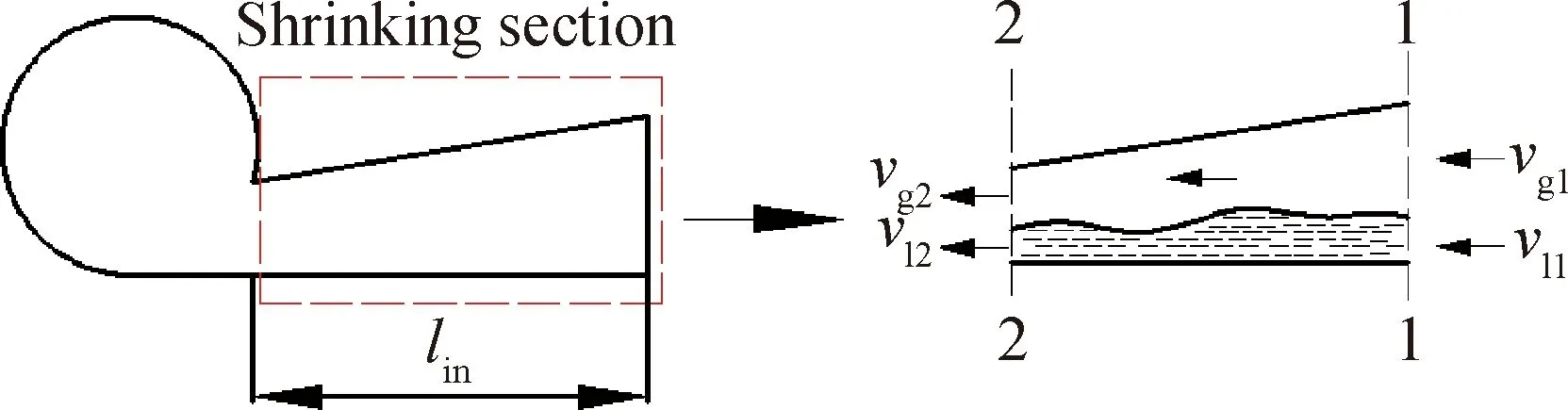
图3 气-液两相流体在入口渐缩段内的流动示意图Fig.3 Diagram of gas-liquid two-phase fluid in theinlet gradual contraction section

(1)

考虑到质量流量(M)、质量流速(G)、速率(v)、质量含气率(x)及截面含气率(α)之间的相互关系[7]，式(1)可转化为：

(2)

由于沿流动方向质量含气率xI保持不变，若假设沿流动方向截面含气率αI也保持不变，式(2)的等号右端第一项便为0，即有：

(3)

式(3)中，dA/dl为沿流动方向截面积的变化率，可以表示为dA/dl=ΔA/lin。A=a2，ΔA=a2-ab。将其代入式(3)，并认为dp/dl≈Δp/lin，即有：

(4)

式(4)所求即为流体流过渐缩截面产生的摩阻压力降。由于流体在下倾管中流动，必然还会产生重位损失，重位压力降的表达式为：

ΔpIg=[ρgαI+ρl(1-αI)]glinsinθ

(5)

将式(4)和(5)加和，可求出GLCC入口收缩压力降。考虑到压力降多表示成阻力系数的形式[9]，即：

(6)

经过对式(4)、(5)的进一步换算，GLCC入口收缩压力降的阻力系数可写为：

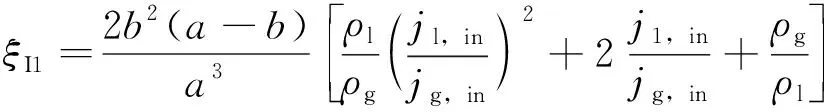
(7)

2.1.2 入口膨胀损失

流体自入口沿切向进入GLCC分离筒体时，会在径向和轴向产生膨胀损失。通常，轴向膨胀损失不易确定，但往往由于其数值较小，所以常在径向膨胀的基础上增加一个修正系数来综合考虑其影响[10]。计算径向膨胀损失时可参照气-液两相流体在入口膨胀段内的流动示意图(如图4所示)。

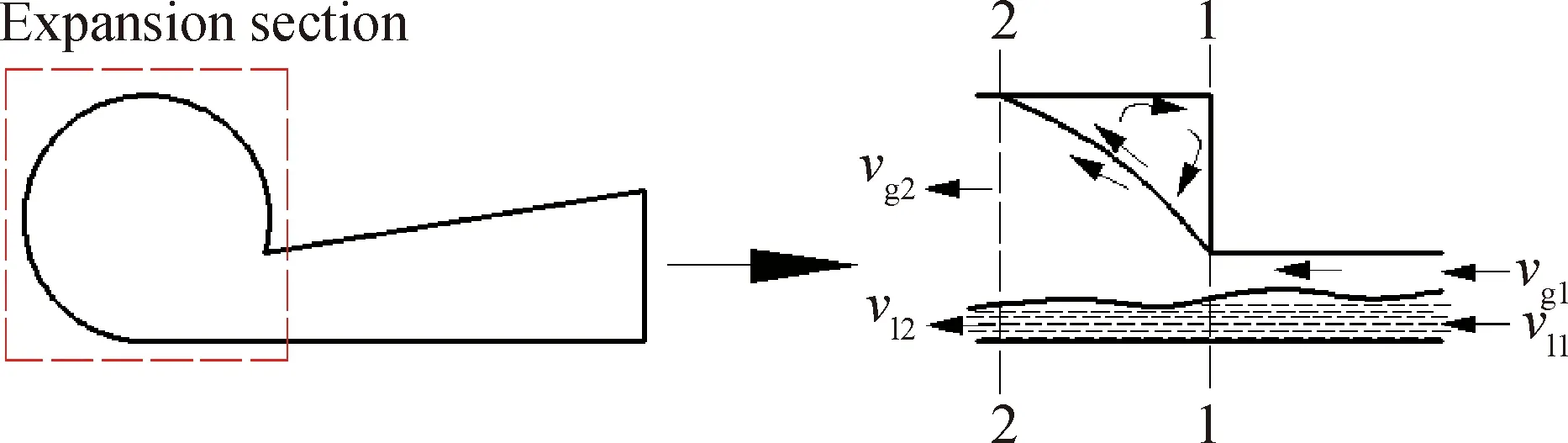
图4 气-液两相流体在入口膨胀段内的流动示意图Fig.4 Diagram of gas-liquid two-phase fluidin the inlet expansion section

将GLCC入口简化为突扩截面，则流体自1-1截面流到2-2截面时，动量方程可写成式(8)[7]。

p1A2+Mg1vg1+Ml1vl1=p2A2+Mg2vg2+Ml2vl2

(8)

根据连续性方程并结合真实流速与质量流速的关系，式(8)可转化为式(9)。

(9)

若将式(9)写成阻力系数的形式，则径向膨胀损失(ΔpIer)即为：

(10)

为了体现轴向膨胀损失(ΔpIez)的影响，在径向膨胀损失(ΔpIer)的基础上添加一修正系数ki(取ki=1.2)。因此，GLCC入口膨胀压力降的阻力系数可写为：

(11)

因此，I区总阻力系数ξI为：

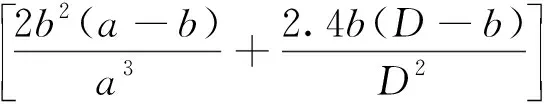
(12)

据式(12)可以看出，只要确定了结构参数及流动参数，即可求出I区总阻力系数ξI。但需指出，在式(12)中，截面含气率αI是未知的，故还需对αI进行求解。本研究中倾斜管的下倾角度θ=27°，周云龙等[11]曾对角度为5°～30°范围的倾斜下降管内的截面含气率进行了研究，并基于分层流模型和实验数据获得了倾斜管底部无量纲液层厚度hl*的表达式(否则，分层流模型需进行迭代计算才能求解出hl*)，即：

(13)

当hl*求出后，即可根据分层流模型的数学关系求出截面含气率αI[11-12]：

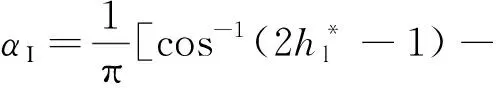
(14)

2.2 筒体(II区)压力降

2.2.1 GLCC上部筒体内气-液流型

流体自入口进入GLCC竖直筒体时会发生分流现象，即：大部分气体和少量液体进入GLCC上部筒体，大部分液体和少量气体进入其下部筒体。在高气/液比情形下，寇杰等[13]、许承炜[14]、贾中会[15]的研究结果均表明：GLCC底流口的气泡带出量不足入口气量的1%，因此认为流过其上部筒体截面的气量等于入口气量。然而，对于分别进入上、下部筒体的液量是不易确定的，与GLCC结构(尤其是入口结构)、工况及流体物性密切相关。事实上，由于入口短路流现象[14,16]及液滴碰壁、破碎、携带、沉积等现象，总会有液体进入上部筒体，进而形成不同的气-液流型。Yue等[16]通过考虑入口短路流现象及液滴携带因素表征出了进入上部筒体内的液体表观速率j′l，可求得对应的液量：M′l=ρlQ′l=ρlj′lπD2/4。鉴于后续需用到该参量，且为了便于对照，将其求解过程列出如式(15)所示[16]。

(15)

由前所述，在GLCC的上部筒体内，气-液两相会呈现出不同的流型。由于不同流型的特征不同，所以不同流型下影响压力降的因素也不尽相同。许承炜[14]针对空气-水体系主要观察到了两类流型，即：旋转环状流(SAF)和旋转搅混流(SCF)；针对空气-水及空气-甘油体系，陈晓慧[4]观察到了相同的流型；Yue等[16]则建立了这2种流型发生转变的判据。旋转环状流和旋转搅混流的流型示意图如图5 所示。

由图5可以看出，当流型为旋转环状流时，筒体压力降的计算应按照气-液相并存区(i区)和气相区(ii区)分别求解再加和(旋转环状流时旋流强度大，仅能维持液体在入口以上约5倍筒体直径的高度处旋转，气芯中的液滴易受离心力作用被补集至液膜，故忽略液滴影响)；而当流型为旋转搅混流时，筒体压力降应按照气-液相共存状态求解(旋转搅混流时旋流强度减弱，气体对液体的轴向携带效应增强，液膜沿管壁不稳定地上下湍动，气-液界面波动加剧，不容忽略液滴影响)。但不论何种流型，其压力降的组成是相同的，即筒体压力降可分为摩阻压力降和重位压力降。下文将根据不同流型的特征分别进行建模。

图5 GLCC上部筒体内气-液两相流型示意图Fig.5 Gas-liquid flow patterns in the upper cylinder of GLCC(a) Swirling annular flow (SAF); (b) Swirling churn flow (SCF)

2.2.2 旋转环状流筒体压力降

(1)气、液并存区(i区)

首先是摩阻压力降。研究气-液两相摩阻压力降的传统方法是用专门定义的折算系数乘以相对应的单相摩阻压力降[17]。其中，折算系数表示为：

(16)

笔者对单气相压力降也进行了测量，用Фg2进行计算，如式(17)所示[7]。

(17)

单气相流过管壁时，摩阻压力梯度可用式(18)表示。

(18)

则，气-液摩阻压力梯度可写为：

(19)

i区重位压力梯度可写为：

(20)

将式(19)和式(20)加和并表示成阻力系数的形式，即有：

(21)

αII可先根据Yue等[16]求出GLCC上部筒体的平均液膜厚度δ再计算，因为二者有如下关系：αII=(1-2δ/D)2。不过在Yue等[16]的模型中，计算δ是一个求解隐函数的过程，虽然可据此求出αII，但过程略繁琐。笔者基于Yue等[16]的模型和滑移比模型[18]，推荐采用式(22)计算αII。

(22)

fi的确定可参考Funahashi等[19]提出的公式计算，即：

fi=0.046[1+17.9(1-αII)]

(23)

关于fi的求法，此处需要指出：在气-液有旋流动中，离心力使得压力在径向上产生新的分布，切向速度的存在会对总体压力降产生贡献，气体径向“挤压”液膜，从而表现为有旋流动中的fi要大于无旋流动的fi[19-20]。

(2)气相区(ii区)

在ii区仅存在气相，气体运动产生的摩阻压力梯度可据式(18)计算，不过纯气体占据的筒体高度为(L-Ls)。结合重位损失，并转化成阻力系数的形式，可得到式(24)。

(24)

然而在式(24)中，fwg是未知的。在无旋单气相流动中，Wallis[21]曾推荐采用式(25)计算fwg,non。

(25)

前文已述，在有旋流动中，离心力对压力降的贡献不容忽略。故笔者根据单气相压力降的实验值Δp23,g及式(18)的形式，通过反算评估了GLCC的fwg[19]，并引入入口气相雷诺数Reg,in来表征旋流的影响，得到式(26)。

(26)

综上，旋转环状流II区筒体损失的阻力系数可统一写为式(27)。

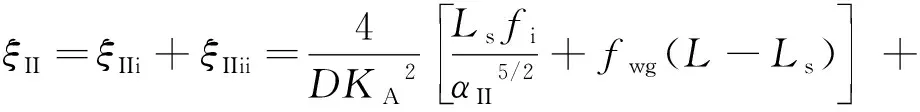
(27)

2.2.3 旋转搅混流筒体压力降

当流型为旋转搅混流时，液膜铺满整个上部筒体壁面，且管道中心携带有液滴[4]。将气芯视为气体与液滴的混合物，可通过引入混合密度ρc来表征该影响。在气芯流道中，总体积流量Qc满足：Qc=Qg+Qd，进一步可写成Mc/ρc=Mg/ρg+Md/ρl，由于ρl≫ρg且液滴质量流量可表示为Md=M′lF′E，因此混合密度ρc的表达式可写为：

(28)

此时Фg2可用式(29)表示[7]：

(29)

则，摩阻压力梯度为：

(30)

重位压力梯度可写作：

(31)

将式(30)和(31)加和且转化成阻力系数，可得到式(32)。

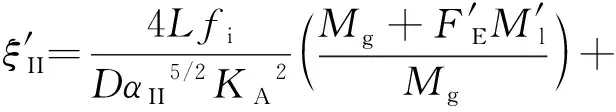
(32)

Azzopardi等[22]曾研究了搅混流型下的液滴携带率，式(32)中的F′E可采用式(33)计算。

F′E=0.6j′l0.35

(33)

2.3 出口(III区)压力降

实际操作中，GLCC出口管会与后续管路连接。根据本研究中GLCC的出口结构(如图1(a)所示)，可将其出口压力降分为4部分：突缩损失、弯管损失、突扩损失及重位损失。另外， III区压力降的计算方法取决于II区气-液相的流型分布：当流型为旋转环状流时，出口仅为气相；当流型为旋转搅混流时，出口为气-液相并存。

2.3.1 旋转环状流出口压力降

当流型为旋转环状流时，出口仅为气相。纯气相压力降的计算方法可参考流体力学相关文献[23]。

(1)出口突缩损失

叶梦佳[24]曾对GLCC上部筒体内的单气相流动进行了数值模拟，结果表明：GLCC的轴向速率与筒体截面的平均气速相近，且随着筒体轴向高度的增大，轴向速率的分布形态无明显变化。根据流体流过突变截面的损失计算方法，考虑动能变化量，可将出口突缩损失的阻力系数写作：

(34)

(2)出口弯管损失

气体流过弯管时，由于局部涡流的产生会造成压力损失，其压力降可利用式(35)计算。

(35)

将式(35)转换成阻力系数和入口速率的关系后，可得阻力系数的表达式为：

(36)

(3)出口突扩损失

设后续管路的直径为Du，本研究中Du>Dg，故会产生突扩损失。突扩损失的阻力系数为：

(37)

理论上讲，气体轴向流经出口还会产生重位损失。但计算表明，该部分压力降占总溢流压力降的比值很小(不超过1%)，故可省略。因此，当流型为旋转环状流时，GLCC出口压力降的阻力系数可统一写作：

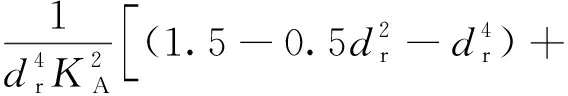
(38)

2.3.2 旋转搅混流出口压力降

当流型为旋转搅混流时，出口为气体与液体的混合物，虽然在气芯中夹带有液滴，但往往由于出口结构的高度较短，液滴对压力降的影响是有限的。为此简化分析，在计算出口压力降时未考虑液滴的影响。此外，认为旋转搅混流时自溢流管流出的气、液流量即是GLCC上部筒体内的气、液流量，因此有xIII=xII，αIII=αII。

(1)出口收缩损失

流体在流经突缩截面时，由于流线只能是一条光滑的曲线，故在紧接的缩口之后会出现一个截面积为Ac的缩颈，如图6所示。气、液相流经突缩截面时的阻力损失则主要来自c-c截面至2-2截面[7]。

图6 气-液两相流体在出口突缩段内的流动示意图Fig.6 Diagram of gas-liquid two-phase fluidin the outlet sudden reduction section

(39)

表1 εc与的关系[7]Table 1 Relationship between εc and

将式(39)进一步转化成阻力系数为：

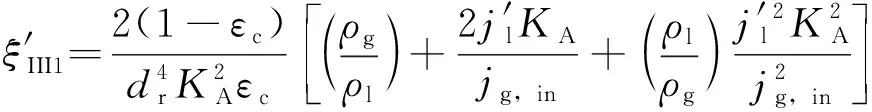
(40)

(2)出口弯管损失

气-液两相流通过弯管时的局部损失主要由2部分造成：一是由于流经弯头产生局部涡流引起的阻力；二是两相滑速比(1/r)发生了改变所产生的阻力。气-液两相流通过弯管的压力降可表示为：

(41)

式(41)中，Δ(1/r)为滑速比增量，Chisholm[25]提出用式(42)计算。

(42)

将式(41)转化为阻力系数后，可得到式(43)。

(43)

(3)出口膨胀损失

与2.1.2节入口膨胀损失的分析方式一致，出口膨胀损失的阻力系数可用式(44)表示。

(44)

此外，计算表明，当气-液两相时，出口重位压力降占比总溢流压力降不大(约2%)，故笔者予以省略。则，当流型为转搅混流时，GLCC出口压力降的阻力系数可统一写作：

(45)

将I、II、III各区的阻力系数分别求解再加和，即可求出GLCC溢流压力降。事实上，当不存在液相时，上述所列阻力系数(式(12)、(27)、(32)、(38)和(45))可退化为计算单气相压力降的阻力系数。

3 GLCC溢流压力降模型验证

笔者基于压力沿程分布理论，分流型建立了GLCC溢流压力降的计算模型。图7为气-液两相及单气相压力降的模型计算值与实验测量值的对比结果。由图7(a)可见，气-液两相的压力降计算值与实验值之间的相对误差约为±20%；由图7(b)可见，单气相的压力降计算值与实验值基本吻合。

基于上述模型，笔者还比较了GLCC的I区、II区和III区的压力降占溢流压力降的比例，结果如表2所示。由表2可知：单气相时，3个区间的压力降占比溢流压力降比例由大到小为III区、II区、I区；气-液两相时，旋转环状流流型对应的3个区间的压力降占比溢流压力降的比例由大到小为III区、I区、II区；旋转搅混流流型对应的3个区间的压力降占比溢流压力降比例由大到小为III区、II区、I区。可以看到，不论是单气相还是气-液两相， III区的阻力损失占比最大。事实上，在GLCC出口处，流体仍存在着强烈的旋转[16,24](尤其是气相)，该部分能量未直接用于流体的分离而被损耗。针对旋风分离器压力降的研究中同样存在该现象，Chen等[10]称其为“动能耗散”，并指出该损耗占比旋风分离器总压力降的60%左右。在GLCC中，III区压力降也包含了这部分“动能耗散”，且III区的压力降占比是最大的。

图7 GLCC溢流压力降(Δp14)的模型计算值与实验测量值对比Fig.7 Comparison between model calculated values and experimental measured values of overflow pressure drop (Δp14) in GLCCSAF—Swirling annular flow; SCF—Swirling churn flow; Cal—Calculated; Exp—Experimental measured(a) Gas-liquid two-phase flow； (b) Single gas-phase flow

表2 GLCC I区、II区、III区压力降(Δp12、Δp23、Δp34)占溢流压力降(Δp14)的比例Table 2 Ratios of pressure drop (Δp12, Δp23, Δp34) of zone I, zone II and zone III with overflow pressure drop (Δp14) in GLCC

陈晓慧[4]曾通过改变液相物性(不同油/水比的甘油溶液，即甘油1(Gly1)、甘油2(Gly2))和溢流管直径(即Dg=30 mm和Dg=40 mm)研究了GLCC的溢流压力降特性。笔者利用所建立的计算模型对陈晓慧[4]提供的实验数据进行了验证，结果如图8所示。结果表明：笔者所建计算模型的计算值与陈晓慧[4]提供的实验值吻合良好，相对误差约在±25%以内。

4 结 论

(1)GLCC溢流压力降包含摩阻损失、重位损失及局部损失，基于压力降沿程分布理论，将GLCC溢流压力降分为3部分：入口(I区)压力降、筒体(II区)压力降、出口(III区)压力降，并考虑GLCC上部筒体内的气-液流型分布及液滴携带因素，结合实验数据建立了GLCC溢流压力降的半理论-半经验模型。

(2)所建立模型既可用于计算GLCC单气相溢流压力降，也可用于计算GLCC气-液两相溢流压力降；模型计算值与实测值进行对比，相对误差在25%以内，预测精度较高。

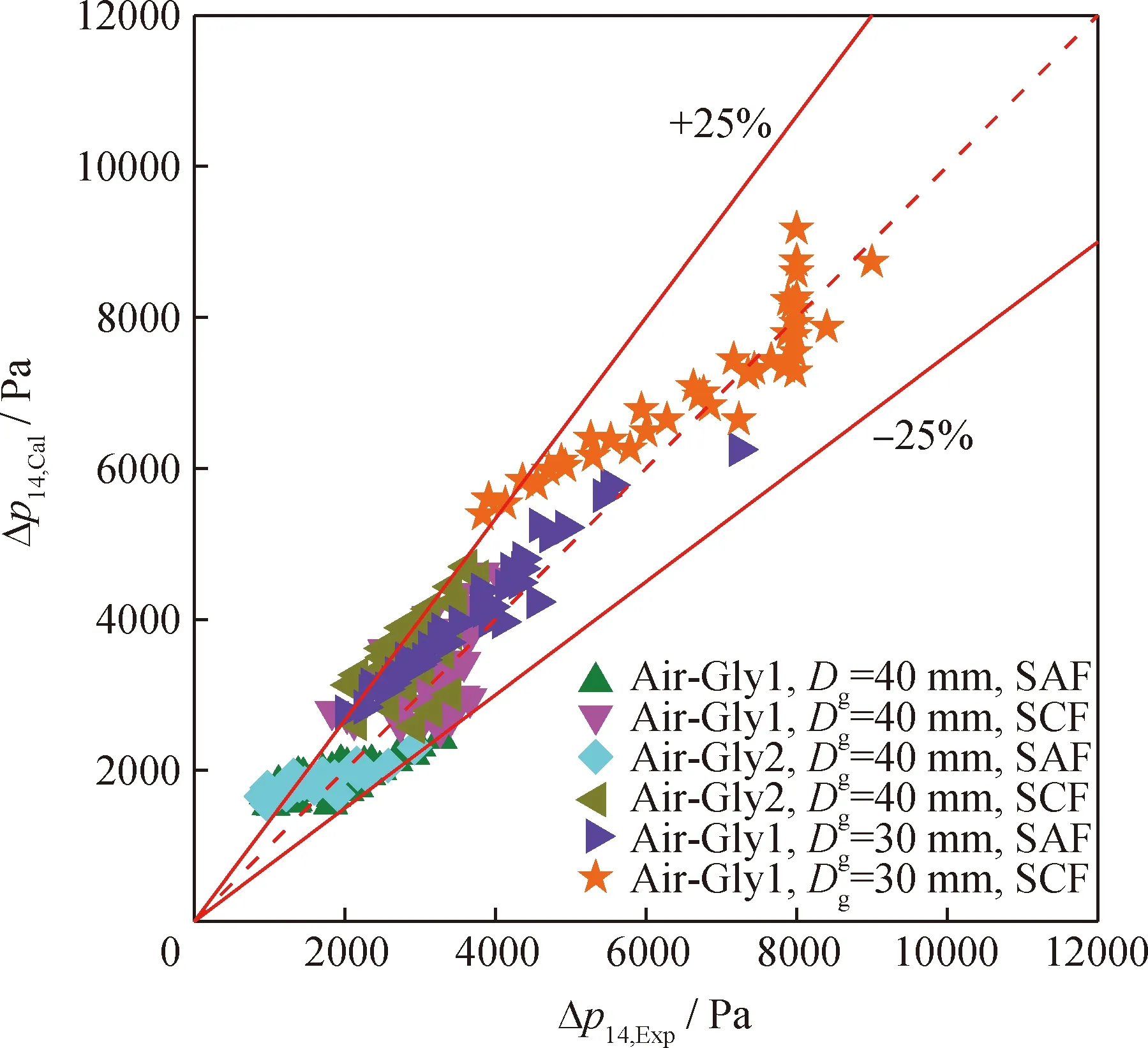
图8 GLCC溢流压力降模型的检验结果Fig.8 Test results of the GLCC overflow pressure drop modelGlycerol solution 1 (Gly1): ρ=1100.4 kg/m3, μ=0.0035 Pa·s, σ=0.061 N/m;Glycerol solution 2 (Gly2): ρ=1121.7 kg/m3, μ=0.0047 Pa·s,σ=0.059 N/m;SAF—Swirling annular flow; SCF—Swirling churn flow

(3)不论是单气相还是气-液两相，III区的阻力损失占GLCC溢流压力降的比例最大，主要原因是在GLCC出口处，气体仍存在着强烈的旋转，该部分能量未直接用于流体的分离而被损耗。

符号说明：

A——流道横截面积，mm2；

Ac——流道收缩端面的面积，mm2；

A2——横截面2-2端面积，mm2；

ΔA——流道横截面积之差，mm2；

a——矩形渐缩喷嘴最小端面长/矩形渐缩喷嘴最大端面边长，mm；

b——矩形渐缩喷嘴最小端面宽度，mm；

D——GLCC筒体直径，mm；

Dg——GLCC溢流管直径，mm；

Du——GLCC后续管路直径，mm；

d——GLCC倾斜管直径，mm；

dA——流道横截面积的微分，mm2；

dh——入口渐缩喷嘴最小端面的水力直径，dh=2ab/(a+b)，mm；

dl——流道长度的微分，mm；

dp、dpf、dpg——压力降、摩阻压力降、重位压力降的微分，Pa；

dr——溢流管直径与筒体直径之比，dr=Dg/D；

d′r——溢流管直径与后续管路直径之比，d′r=Dg/Du；

dz——管道长度的微分,mm；

FE——倾斜管内的液滴携带率；

F′E——旋转搅混流时的液滴携带率；

FS——入口短路流率；

fi——气-液界面间摩擦系数；

fwg——单气相时气体与壁面间摩擦系数；

fwg,non——无旋流单气相时气体与壁面间摩擦系数；

G——气、液相总质量流速，kg/(s·m2)；

Gc——流道收缩端面的总质量流速，kg/(s·m2)；

Gg——气体质量流速，kg/(s·m2)；

Gl——液体质量流速，kg/(s·m2)；

G1——横截面1-1处液体质量流速，kg/(s·m2)；

g——重力加速度，m/s2；

hl——倾斜管底部液层厚度，mm；

hl*——倾斜管底部无量纲液层厚度；

jg——筒体轴向气体表观速率，m/s；

jg,in——入口气体表观速率，m/s；

jgo——溢流管内气体折算速率，m/s；

jl,in——入口液体表观速率，m/s；

j′l——上部筒体内液体表观速率，m/s；

K——求解倾斜管圆周顶层液膜厚度的系数；

KA——入口面积比，KA=πD2/4ab；

k——倾斜管底部液层厚度系数；

ki——GLCC一区膨胀损失的修正系数，取ki=1.2；

L——GLCC上部筒体高度，mm；

Ls——旋转环状流时液体占据的GLCC上部筒体高度，mm；

l——流道长度，mm；

lin——入口喷嘴长度，mm；

M——气、液体总质量流量，kg/s；

Mc——气芯混合质量流量，kg/s；

Md——气芯中液滴质量流量，kg/s；

Mg——气体质量流量，kg/s；

Ml——液体质量流量，kg/s；

M′l——上部筒体内液体质量流量，kg/s；

p1、p2——横截面1-1和2-2处的压力，Pa；

Δp——压力降，Pa；

Δpee、Δp′ee——气相、气液两相流过弯管的压力降，Pa；

Δp′es——气液两相流过III区突扩段的压力段，Pa；

Δpf、Δpg——摩阻、重位压力降，Pa；

Δp12——GLCC入口(I区)压力降，Pa；

Δp14——GLCC溢流压力降，Pa；

Δp23——GLCC筒体(II区)压力降，Pa；

Δp23,g——单气相流过GLCC筒体(II区)的压力降，Pa；

Δp34——GLCC出口(III区)压力降，Pa；

ΔpIer、ΔpIez——GLCC I区径向、轴向膨胀压力降，Pa；

ΔpIf、ΔpIg——GLCC I区摩阻、重位压力降，Pa；

Qc——气芯混合体积流量，m3/h；

Qd——气芯中液滴体积流量，m3/h；

Qg——气体体积流量，m3/h；

Ql——液体体积流量，m3/h；

Re——溢流弯管的曲率半径，mm；

Reg——上部筒体内气相雷诺数；

Reg,in——入口气相雷诺数；

Δ(1/r)——滑移比增量；

vg——气体真实速率，m/s；

vg1、vg2——横截面1-1、2-2的气体真实速率，m/s；

vl——液体真实速率，m/s；

vl1、vl2——横截面1-1、2-2的液体真实速率，m/s；

v′l1、v′l2——上部筒体液体流经1-1、2-2截面的真实速率，m/s；

vsg——倾斜管内气体表观速率，m/s；

vsl——倾斜管内液体表观速率，m/s；

xI、xII、xIII——GLCC I区、II区、III区的质量含气率；

αI、αII、αIII——GLCC I区、II区、III区的截面含气率；

β——体积含气率；

β′——计算倾斜管内的液滴携带率系数；

δ——截面平均液膜厚度，mm；

δin,top——倾斜管圆周顶层的液膜厚度，mm；

εc——流道面积收缩比；

θ——倾斜管与水平面间角度，°；

μg、μl——气、液体动力黏度，Pa·s；

ξ——阻力系数；

ξI、ξII、ξIII——GLCC I区、II区、III区的阻力系数；

ξI1、ξI2——GLCC I区入口收缩、入口膨胀阻力系数；

ξIIi、ξIIii——GLCC II区气-液相并存区、气相区的阻力系数；

ξIII1、ξIII2、ξIII3——旋环流时GLCC III区收缩损失、弯管损失、突扩损失的阻力系数；

ξ′II、ξ′III——GLCC II区、III区旋转搅混流流型对应的阻力系数；

ξ′III1、ξ′III2、ξ′III3——旋转搅混流时GLCC III区收缩损失、弯管损失、突扩损失的阻力系数；

ξ0——出口弯管损失的阻力系数；

ρc——流体混合密度，kg/m3；

ρg、ρl——气、液体密度，kg/m3；

ρm——流体流动密度，kg/m3；

σ——表面张力，N/m；

Фg2、Фl2——气、液相折算系数。