一类Choquard型拟线性Schrödinger方程解的存在性

张晓静，贾 高

（上海理工大学 理学院，上海 200093）

1 问题的提出

研究了如下形式的Choquard型方程解的存在性问题：

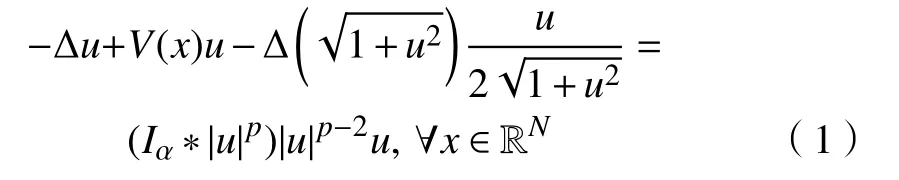
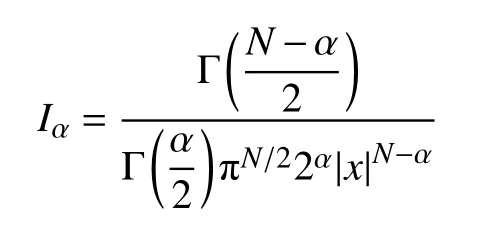
方程（1）与如下形式的拟线性Schrödinger方程的驻波解密切相关：

在以往的研究中，当方程(2)中取l(s)=s时，大量学者利用变分方法、临界点理论等解决了方程解的存在性和多重性等问题。但是，关于l(s)=(1+s)1/2的研究较少。对于Choquard型半线性方程现已有许多研究，受文献[5]的启发，本文讨论Choquard型拟线性方程。因为，方程（1）中的非线性项是非局部的，无法直接使用处理局部问题的方法解决该拟线性问题。

现假设V(x)满足以下条件：

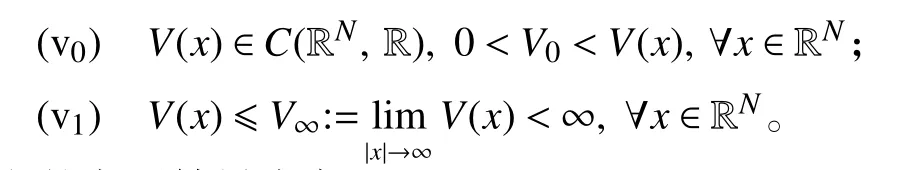
本文的主要结果为定理1。

定理1若条件(v0),(v1)成立，则问题(1)在H1(RN)中至少存在一个非平凡解。

2 预备知识

在本文中，对工作空间H1(RN)赋予范数‖u‖2=符号|u|p表示通常的Lp(RN)空间函数u(x)的范数。

首先考虑变量替换

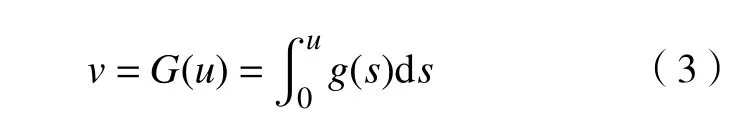
引理1[6]对于函数g(t)和G-1(t)有如下性质：

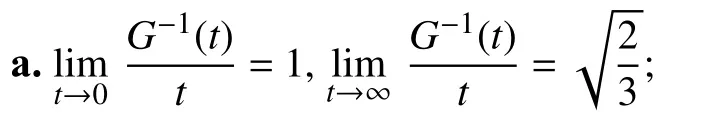
b.对于所有的t∈R ，有

c.对于所有的t∈R，有

引理2[5]（Hardy-Littlewood-Soboloev不等式）若g(x)∈Lr(RN)，h(y)∈Ls(RN)，则存在常数C，使得

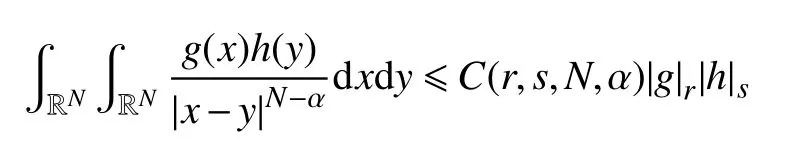
其中，r,s,α,N满足r,s＞1，0＜α＜N，

引理3若v∈Lpr(RN)，则根据Hardy-Littlewood-Sobolev不等式可知

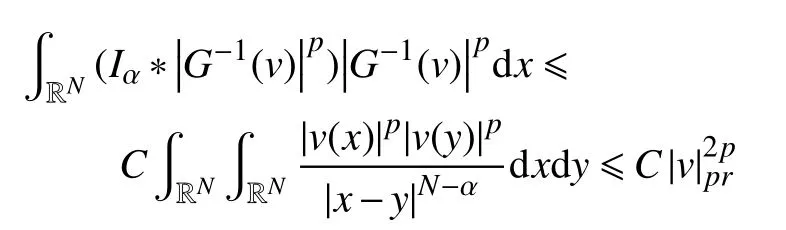
若pr∈[2,2∗)，那么，另外，由Sobolev嵌入定理可知，当且仅当

注意到方程（1）对应的能量泛函

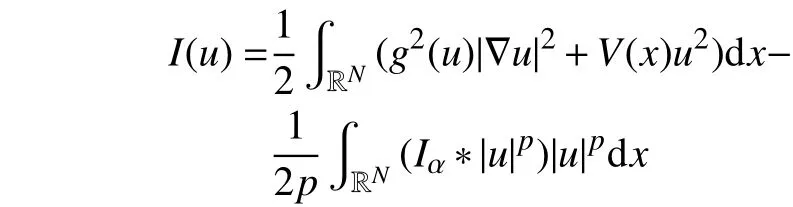
但是，在H1(RN)空间上该能量泛函I(u)可能无定义。因此，利用式(3)的变量替换v=G(u)将泛函I(u)转化为如下形式：

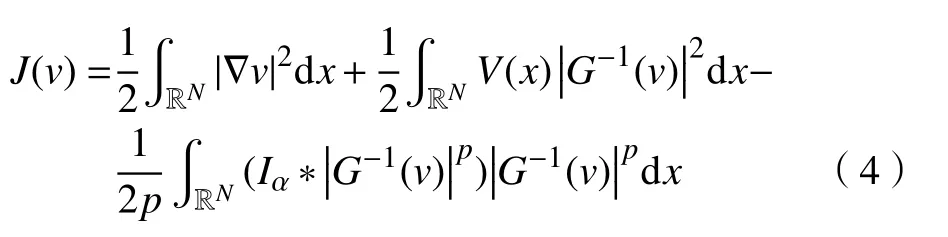
根据引理1和引理3，J在H1(RN)中是有定义的，并且J(v)∈C1(H1(RN),R)，对于任意的φ∈H1(RN)，有

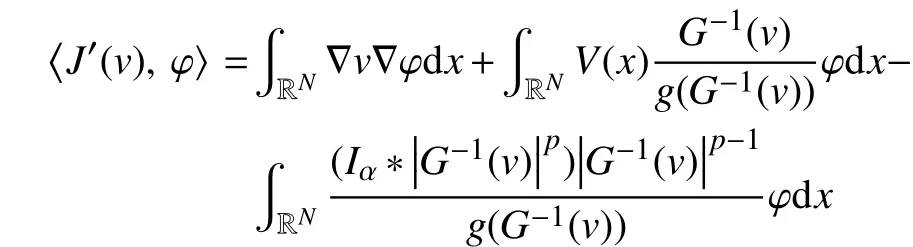
进一步由引理1和引理2可知，如果v∈H1(RN)是泛函J的临界点，则u=G-1(v)∈H1(RN)，同时u也是I的一个临界点。

3 主要引理及定理1的证明

首先验证泛函J具有山路几何结构及其(PS)序列的有界性，其次将给出定理1的证明。

引理4若假设条件(v0),(v1)成立，那么，存在ρ,α＞0和e∈H1(RN){0}，使得

a．当‖v‖=ρ时，有J(v)＞α；

b．当‖e‖＞ρ时，有J(e)＜0。

证明结合式(4)、引理1、引理3和Sobolev嵌入定理，可得

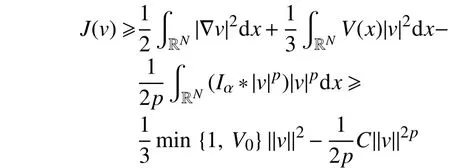
根据p＞1，可知J(v)在v=0处具有局部最小值。

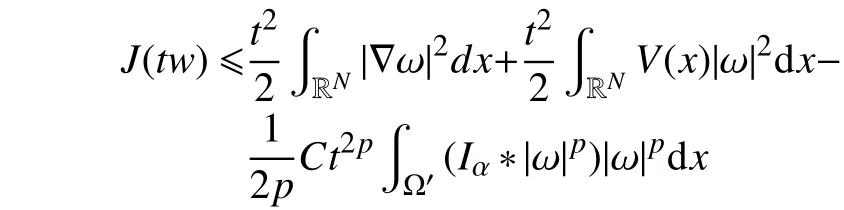
由于p＞1，因此，当t→∞时，J(tω)→-∞。

综上，泛函J满足山路几何结构。证毕。

称序列{vn}是泛函φ的一个(PS)序列，若当n→∞时，有φ(vn)→c，φ′(vn)→0。那么，结合引理4及文献[7]中的山路定理，可得泛函J在对应的山路水平d处有(PS)d序列{vn}，即J(vn)→d，J′(vn)→0。

引理5在假设条件(v0),(v1)下，J的(PS)序列{vn}在H1(RN)中有界。

证明令{vn}⊂H1(RN)为泛函J的(PS)序列，则满足

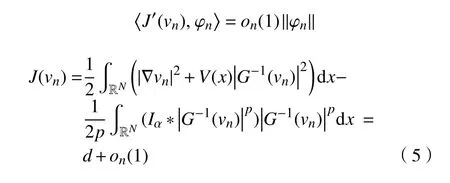
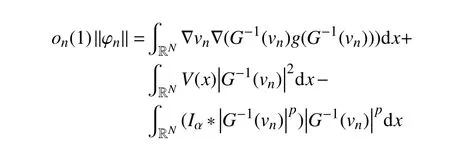
根据引理1可知，

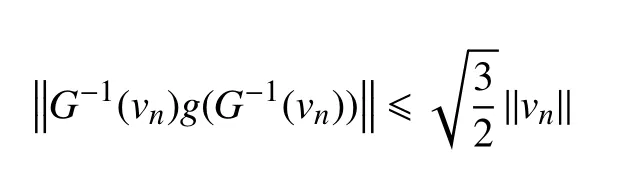
从而，

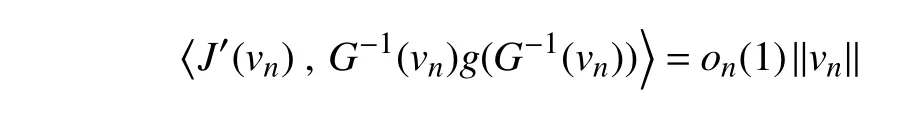
进而可以推导出

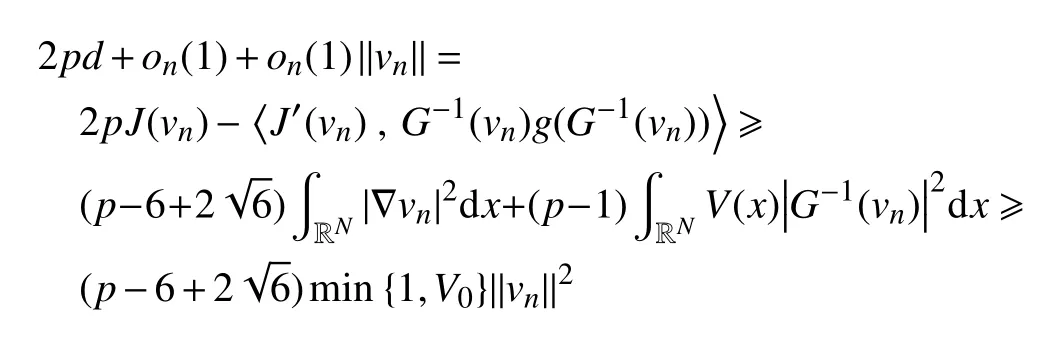
引理6假设条件(v0),(v1)成 立，那么，J有一个临界点。

证明设{vn}⊂H1(RN)是由引理4中给出的泛函J的有界(PS)序列，则存在子列{vn}（仍记为本身）及v⊂H1(RN)，使得vn⇀v（在H1(RN)中），vn→v（在中）, 其中，p∈[2,2∗)，vn→v，a.e.x∈RN。

现证明v是J的临界点，也就是说J′(v)=0。由于在H1(RN)中稠密，所以，为证明J′(v)=0，只需要证明对于所有有〈J′(v),φ〉=0。因为，

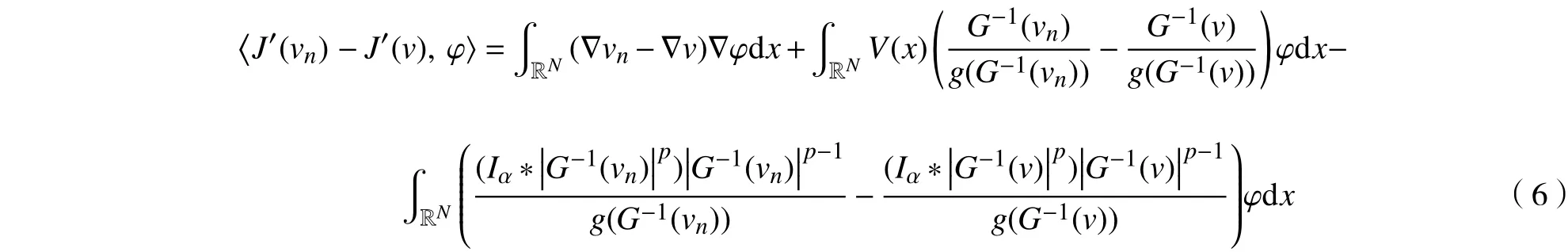
当n→∞时，式(6)的右边收敛到0，进而得出〈J′(v),φ〉=0。中，则由假设条件

首先，在Kφ:=suppφ中，有其(v1)，有下式成立：

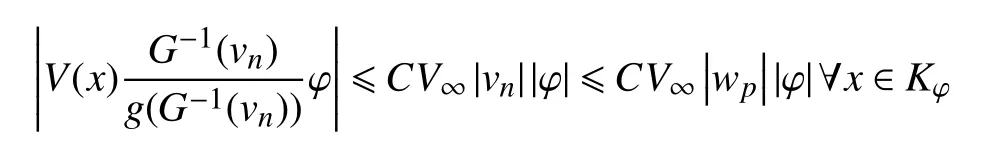
故由勒贝格控制收敛定理可得

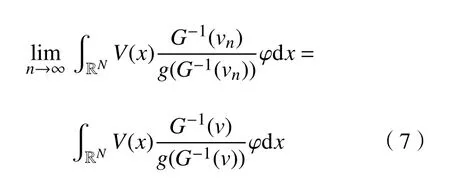
其次，对于式(6)右边的第三项，有

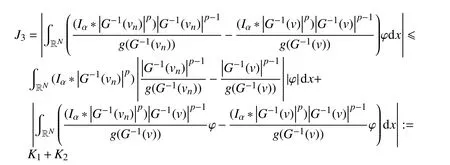
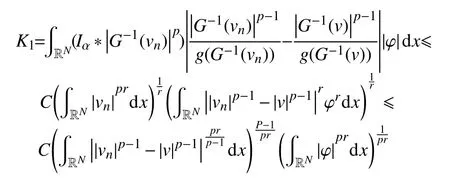
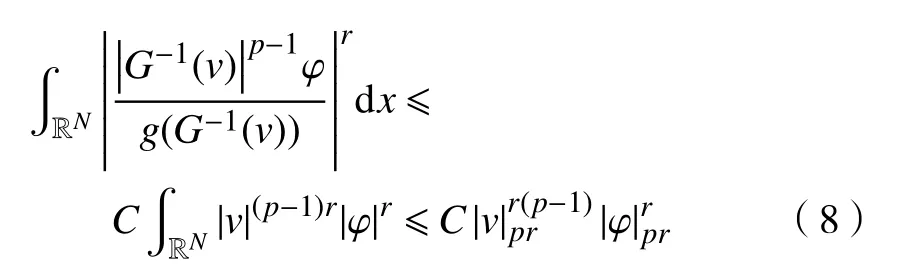
因为，pr∈[2∗,2)，故设

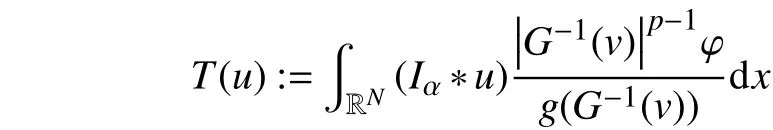
由式(8)可知，T:Lr(RN)→R 是一个连续线性泛函。又{vn}在H1(RN)中有界，则因此，当n→∞时，即K2→0。

所以，当n→∞时，有J3≤K1+K2→0。综上，〈J′(vn)-J′(v),φ〉→0，即v是J的临界点。证毕。

如果v≠0，则原问题即有非平凡解。为了证明v≠0，考虑以下极限泛函及其导数：

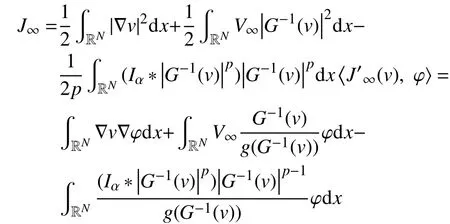
引理7假设条件(v0),(v1)成立，设{vn}⊂H1(RN)是泛函J的有界(PS)序列（由引理4中给出）且{vn}⇀0，则当n→∞时，有J∞(vn)→d和

证明因为，{vn}⊂H1(RN)是泛函J的有界(PS)序列，则存在M1＞2V∞，使得又根据假设条件(v1)及在中有vn→0可得，对任意的ε＞0，存在M＞0，使得当n充 分大时，有

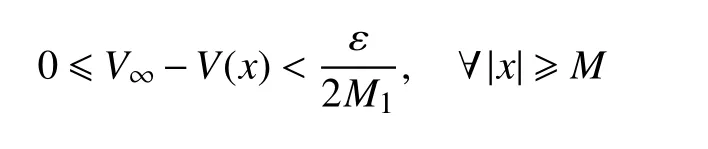
和

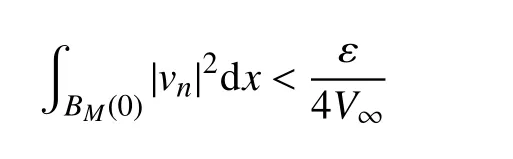
因此，当n→∞时，有

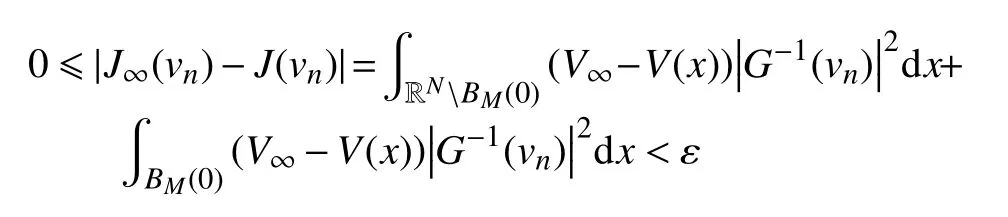
类似地，当n→∞时，可有

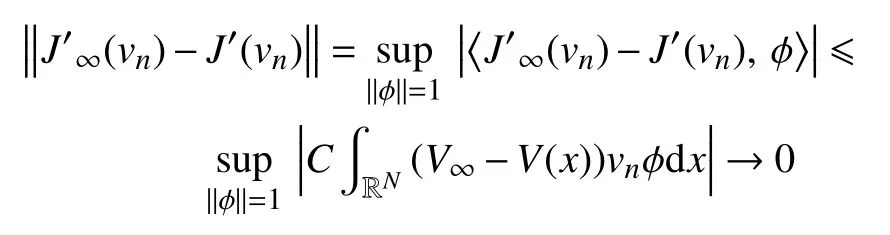
这样便完成了引理7的证明。

定理1的证明根据引理7，为了证明定理1，只需要证明v≠0。现利用反证法来证明。

首先若假设条件(v0),(v1)成立，且{vn}⊂H1(RN)是J的有界(PS)序列，那么，对于{vn}来说，存在一个序列{yn}⊂RN和r,σ＞0，使得当n→∞时，有|yn|→∞，且

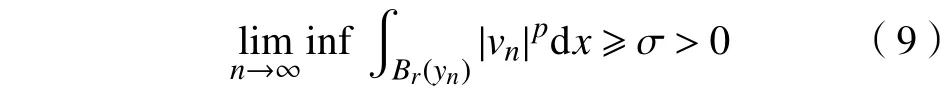
其中，2≤p＜2∗。事实上，若式（9）不成立，则有则根据Lions集中紧性结果可得，在空间中，vn→0（2＜p＜2∗）。进一步利用引理1及引理3可推出

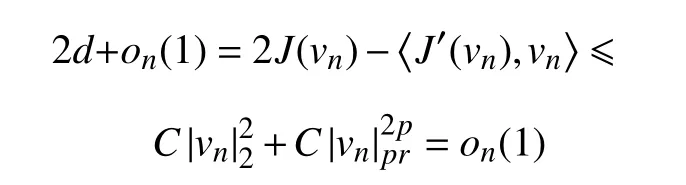
这是矛盾的。故式（9）成立。

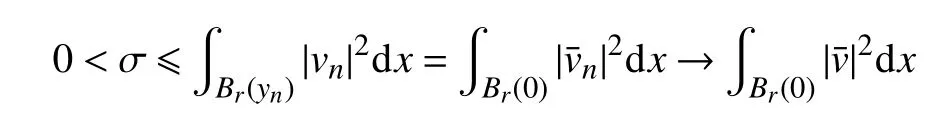
其次，由引理1和Fatou引理可得

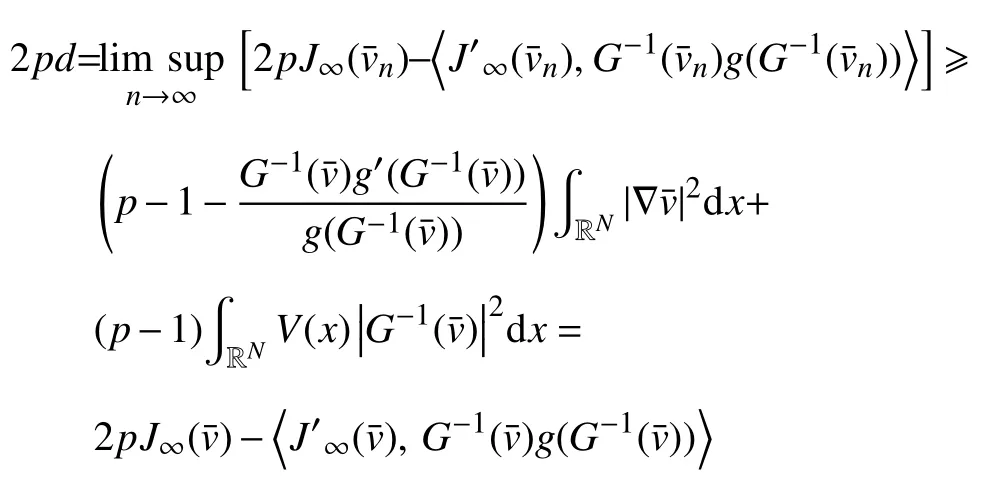
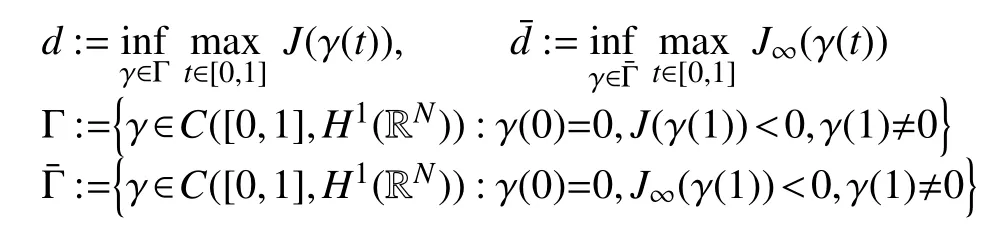
借助文献[8]中类似的方法，可选取一个特定的路径γ:[0,1]→H1(RN)，其中，γ满足

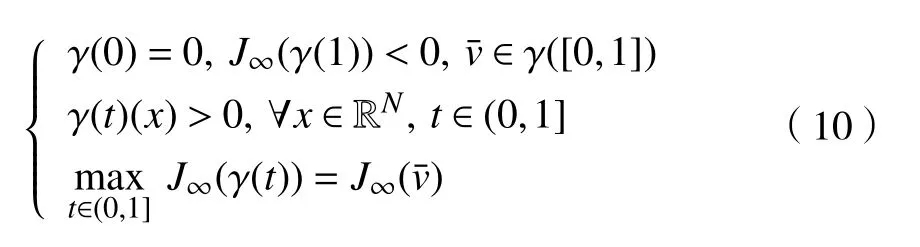
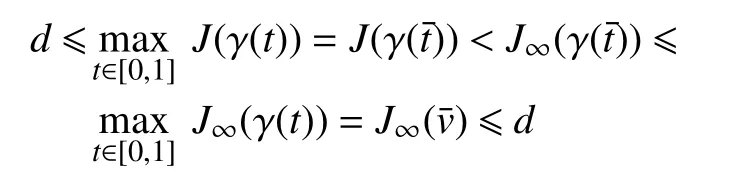
这是一个矛盾的结果。因此，从以上论证可以得出v是J∞的一个非平凡临界点。