求解大规模稀疏Min-CVaR投资组合模型的对偶方法

王云龙，沈春根

（上海理工大学 理学院，上海 200093）

1 背景与现状

随着我国金融市场的形成和发展壮大，金融投资已成为我国居民日常生活中的一个热门话题。金融投资组合可以通过挑选特定的投资标的资产，在有限的投资资本下，降低风险并提高期望收益。这种在风险与收益之间的权衡，关键在于不同投资标的之间配资比例的确定。经典的马科维兹均值−方差模型（Mean-Variance，MV）将投资组合中标的资产的配资问题转化为一个带约束的二次规划问题[1]，通过求解此最优化问题，确定在获得期望收益时使风险最小或在可承受风险内期望收益最大的投资配比[2]。后续的研究中，不少学者在此基础上继续探索如何使风险最小并且收益最大[3-6]。在MV模型中，风险通过方差定义，并且假设标的资产的收益率服从正态分布或椭圆分布，这种假设在金融投资领域应用中并不完全可行。首先，由于方差的对称性，无论正向偏离还是负向偏离均会被同等考虑进模型中，即如果减少方差会带来正向偏离和负向偏离的同步减小，投资组合的收益同时被对风险的管理所影响，因而以方差作为风险度量的MV模型一直广受诟病[7]。其次，MV模型需要计算所有标的资产收益率的协方差矩阵，这在大规模场景下会使计算成本急剧增加，求解极其困难。

现实中的风险度量倾向于区分正向偏离和负向偏离[8]。Markowitz[9]曾提出半方差（Semi-Variance）模型度量低于平均水平的收益波动性（风险）。在险价值（Value-at-Risk，VaR）[10]和 期 望 损 失（Expected Shortfall，ES，或称条件在险价值，Conditiona lValue-at-Risk，CVaR）[11]是目前广为流行的风险度量，它们注重于对尾部损失（风险）的度量[12]。对VaR和CVaR数学性质的分析和比较可见Rockafellar和Uryasev的文章[13]及Pflug的相关书籍[14]。虽然CVaR作为VaR的补充统计量而非可以替代VaR，但值得指出的是，CVaR具有一致性风险度量的良好性质，它考虑了超VaR部分的损失，对尾部风险的衡量更准确和稳定[14-16]。求解Min-CVaR模型实际上是一个线性规划问题，而当输入情景数据（行数）过多时，此线性规划需要增加等量级的辅稀疏诱导性质的惩罚项有L1范数和L0范数。L0可以直接衡量解中非零元的个数，稀疏效果最好，而实际上是NP-hard的问题，求解不够高效。文献[21]研究以L1范数为惩罚项的稀疏马科维兹投资组合模型，并分析了引入L1范数带来的理论影响和实际意义。本文选择L1范数作为惩罚项加入Min-CVaR模型的目标函数中，L1可以取得较少的非零元，相当于挑选较少的标的资产。相比于L0范数，L1范数会惩罚较大的元素，相当于分散配资比例避免极端头寸。文献[6]中的原始模型很难通过对偶模型加速。本文在文献[25]的基础上改进了求解稀疏投资组合问题的优化模型。相比之下，本文引入L1范数作为稀疏项有利于对偶模型求解。L1范数作为惩罚项，会使原本投资组合优化模型变得复杂，如L1范数具有非光滑性。关于带L1范数的优化问题一直被广泛关注[26-28]。此外，不同于文献[25]，本文增加了允许卖空的市场环境。因而，利用对偶思想求解稀疏投资组合模型，通过变换原始问题，降低了求解难度，可以极大地提高大规模稀疏Min-CVaR投资组合模型的计算效率，这对在大数据时代高频助变量，且约束的数目也急剧增加，这对一般线性规划求解而言极具困难。实际上，使用最新的商业求解器（如CPLEX、GUROBI）求解，当情景数据在十万量级，资产个数在百千量级时，需要花费数个小时。为了避免这种情况，不少学者设计了各种解决思路，如情景分解方法[17-18]、二阶段方法[19]、切平面法[20]。上述研究均没有考虑解的稀疏性要求。稀疏性目标可以利用一系列稀疏方法优化实现，通过添加惩罚项或者增加约束，使优化问题的解具有较少的非零元素。常见的具有稀疏模型虽然具有以上优点，但增加稀疏约束或惩罚项会使模型更加复杂，尤其在数据规模很大的情况下。目前国内外对稀疏投资组合模型的研究[22-24]中，情景数据的规模仍为几百个或一千多个，在大数据时代，尤其是高频交易场景下，利用超大规模历史情境数据建立投资模型是一种趋势。文献[25]曾利用对偶方法求解投资组合优化问题，文献[6]利用SCAD函数作为惩罚项并利用QR技术求解稀疏的投资组合优化问题，但交易场景下高效构建投资组合模型具有一定的指导借鉴意义。

2 稀疏Min-CVaR模型

2.1 基本概念

本文假设投资组合中有N个标的资产，样本的时间长度为T，投资组合的数据观测记为R=[R1,···,RN]∈RT×N，资产i在时间t的收益率记为假设资产i的配资比例（权重）记为则投资组合在t时刻的收益率为

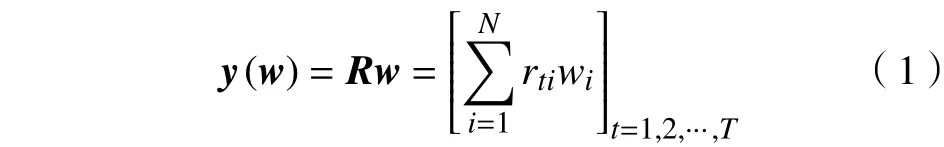
式中：y(w)∈RT；记pt∈[0,1]为过去每个时刻可能发生的概率(p∈RT,1Tp=1)，并假设pt=1/T，即所有时刻重现的概率相等，则投资组合的期望收益率为

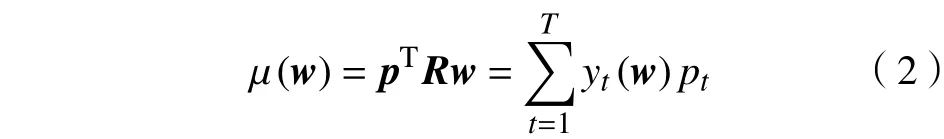
上述1（后续的0）为维数与上下文匹配的全1（0）向量或矩阵。投资组合各标的资产间的协方差矩阵记为Σ=cov(R)∈RN×N，Σ具有对称性和半正定性。整个投资组合收益率的方差为σ2(w)=wTΣw。

2.2 条件在险价值CVaR

在险价值VaR有3个关键要素：置信水平或概率α，时间段Δt，损失值VaRα。即基于当前时刻t的信息，预测在一定置信水平 α下经过时间段Δt后的上限损失值，即未来Δt时间后损失超过VaRα(w)的概率为1-α。离散情况下的数学表达为

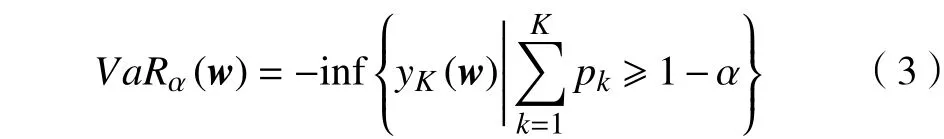
式中：yk(w),k=1,2,···,K满足y1(w)≤y2(w)≤···≤yK(w)；pk为yK(w)对应的概率。CVaR定义为超过VaR损失的期望值，离散情况下CVaR的数学表达为

2.3 标准Min-CVaR模型

最小化式（4）等同于最小化式（5），即

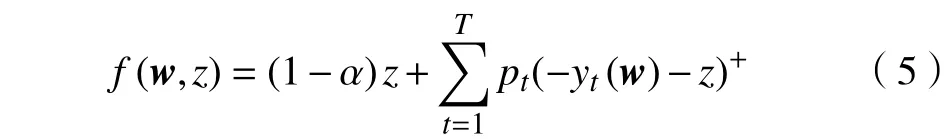
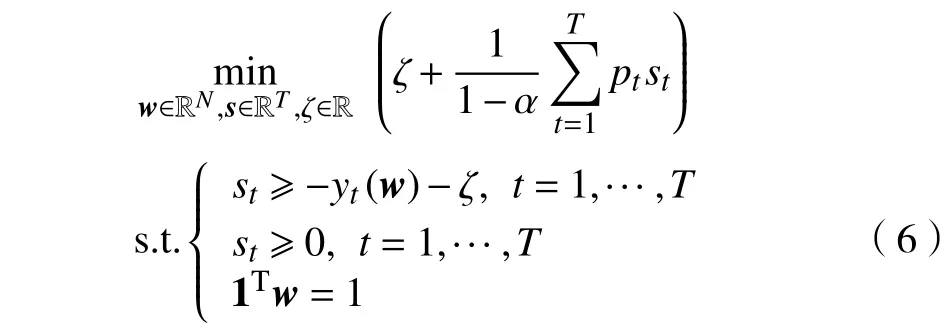
因此，求解最小化模型（6）可以同时得到配资比例wopt、在险价值VaR=ζopt和条件在险价值由于模型（6）引入辅助变量s∈RT，使得总的变量个数为T+N+1，同时增加了T个结构复杂的约束，大规模情景下这无疑会使线性规划问题的求解难度增加。

2.4 稀疏Min-CVaR模型

在上述Min-CVaR模型中，配资比例是在所有标的资产之间计算的。首先模型求解是分散在所有标的资产上的，无法实现挑选标的资产的目的，其次，在假设允许卖空时，为了实现最优，模型会产生在某些标的资产上的极端头寸（比如看跌资产i并借10倍杠杆，看涨资产j并配资11倍）。通过增加L1范数约束可以避免以上问题，‖w‖1=会对数值较大的权重加以约束，可同时实现只挑选少数标的资产以及均衡被挑选标的资产间的配资比例，达到权重的稀疏性（较多零元）。稀疏Min-CVaR模型可以表达为

模型（7）中可以通过调整参数n控制解的稀疏度，n越大，最优解中的非零元个数越多且分布范围越大。当n→+∞，带L1范数约束的Min-CVaR模型将退化为标准的Min-CVaR模型。在一定条件下，模型（7）的等价形式为

其中，λ＞0为调和参数。对于模型（8），其拉格朗日函数为

其中，∂‖w‖1表示L1范数的次微分。

则模型（8）的拉格朗日对偶函数为

得对偶模型：

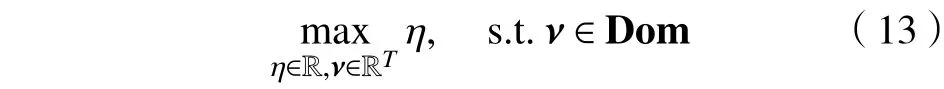
其中，Dom为满足式（12）中约束(I)～(III)的集合。模型（13）中变量总数为T+1，约束总数为2(T+N)+1。实际上，由于约束(II)为简单的盒子约束（boxconstraints），不会影响求解问题的复杂程度，所以只有结构稍微复杂的约束(I)和(III)会影响问题求解，因而影响对偶模型（13）求解难度的约束个数只受股票池规模（矩阵R的列数N）的影响。当计算大规模情景数据时（T≫N），求解原始模型的难度骤升，而通过对偶方式则会极大地提升求解效率。

3 数值实验

在数值实验中，本文使用模拟数据和真实数据测试求解对偶模型策略的时间优越性。首先介绍了利用三因子模型模拟生成大规模数据，以及选择调和参数的具体步骤，结果显示，在模拟数据上，随着情景规模的增加，对偶模型提升求解效率的表现更显著。另外，给出了在真实高频数据（标普500）上的试验结果，同时和标准Min-CVaR模型进行了对比，结果显示，稀疏模型可以明显地增加解的零元个数，达到挑选标的资产的目的，对偶模型能够有效提升求解效率。本文试验环境为MATLB2017b，Inter（R）Core（TM）i5-3230M，CPU@2.6 GHz，RAM 8 GB，GURIOBI求解器通过MATLB2017b调用。

3.1 模拟数据

假设收益矩阵记为R∈RT×N，本文根据经典的三因子模型[29]生成随机的收益矩阵为

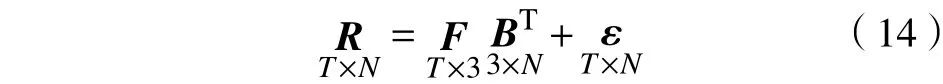
式中：F为因子矩阵，服从多元正态分布N(µF,ΣF)；B为因子载荷矩阵，服从多元正态分布N(µB,ΣB)；假设噪声矩阵 ε与因子矩阵独立并且服从伽马分布Γ(aε,bε)。上述的分布参数选择依据文献[29]中的表1，这里重新给出：

文献[30]进行了大规模情景数据模拟实验（T=50000），本文也采用相似规模设置，不同的是，本文收益矩阵由式（14）描述的三因子模型生成。

通过表1可以发现在计算大规模情景数据时，对偶方法在计算效率上具有明显的优越性。表1统计了每个问题计算20个 λ对应的问题的总耗时，λ∈λmax[10-3,1]，其中λmax是可确定的合适的调和参数，使得∀λ≥λmax时，原问题（8）的最优解不再变化。实际上，当 λ非常小的时候，对偶模型的求解效率提升不太明显，稍微比原始问题快2～3倍；当 λ较大的时候，效率提升至10倍左右（依赖于收益矩阵的规模，情景维数越大，提升效果越显著）。具体地，随着 λ的增大，求解原始模型的耗时呈上升趋势，求解对偶模型的耗时呈下降趋势。图1展示了T=50000,N=20,α=0.9时，λ大小对求解时间的影响（其中i对应于 λ序列的位次，i/20=-3lg(λ/λmax),i=1,···,20，i越小，对应的 λ越大）。从数学优化的角度看，当λ→0时，L1范数的影响降低，原始模型逐渐趋向于标准Min-CVaR模型，即模型变得简单，而对偶模型中约束（I）的上下界间隙越来越小，即模型变得复杂。因而当 λ非常小时，求解对偶模型的效率提升相对较小。一般情况下，模型倾向于简洁时，会选取稍大的 λ值，此时，求解对偶模型的效率提升相对较大。

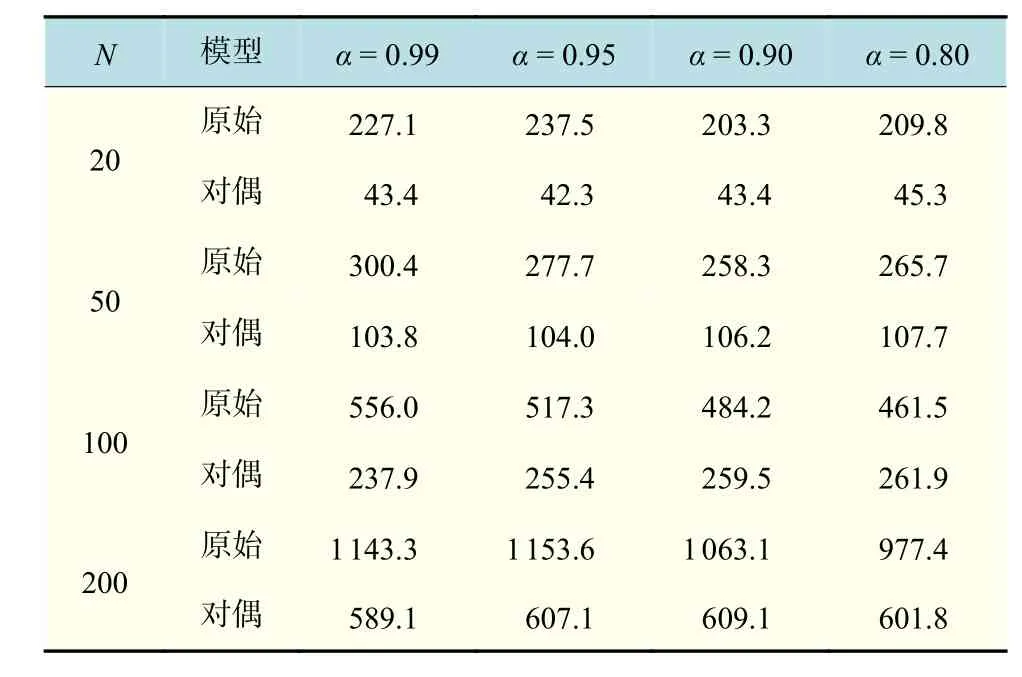
表1 不同概率水平下计算整个 λ路径所需时间（T=50 000）Tab.1 Time consuming for solving a path of λ with different probability levelss

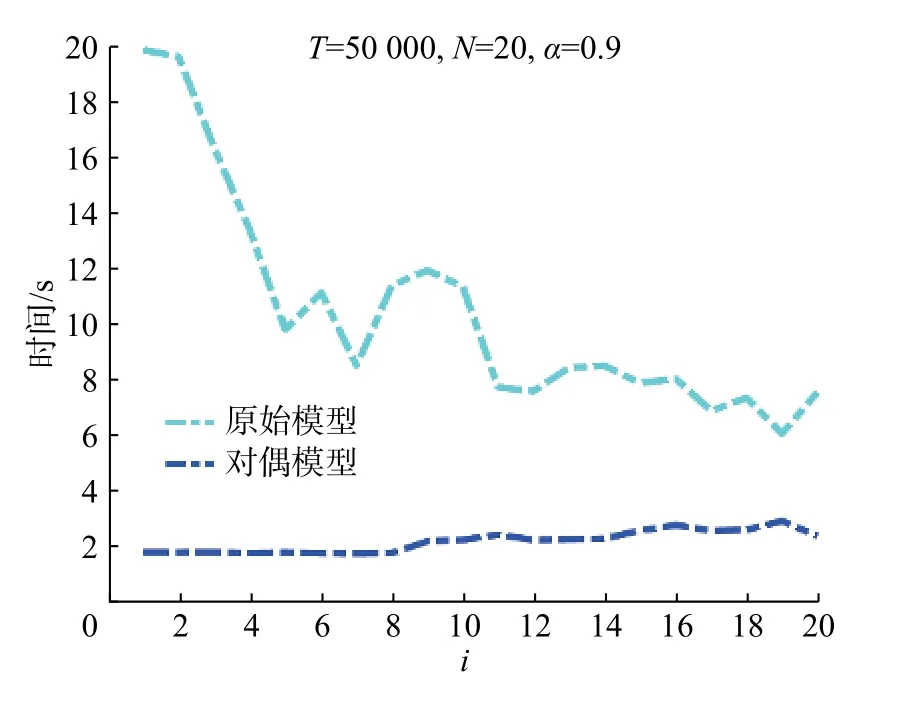
图1 求解对偶模型与原始模型的耗时变化Fig. 1 Time paths for solving the primal and dual model

3.2 参数选择

在原始模型和对偶模型中，参数 λ扮演着不同的角色，但都会导致解的稀疏性（0除外）。λ在原始模型中被称为调和参数，具有平衡稀疏性和最小化目标函数的作用。调和参数越大，获得的解稀疏性越高（零元越多）。在对偶模型中 λ是复杂结构约束（I）的上下界，影响着约束的严苛程度，根据对偶性质，原始问题也是其对偶问题的对偶问题，原始变量与对偶问题的对偶变量间存在一一对应关系。较大的 λ意味着对偶问题中约束的上下界距离较远，则积极约束的个数会相应减少，积极约束集的大小与对偶问题的对偶变量非零元个数一致，即原始问题的解非零元少（稀疏性大）。模型参数的选择有不同的准则，如交叉检验（Cross-Validation）[31]、赤池弘次（Akaike）信息准则（AIC）[32]。本文选取贝叶斯信息准则（BIC）[33-34]作为判断不同参数下模型好坏的依据，BIC越小则模型越优越。记wλ为问题（8）的最优解，则

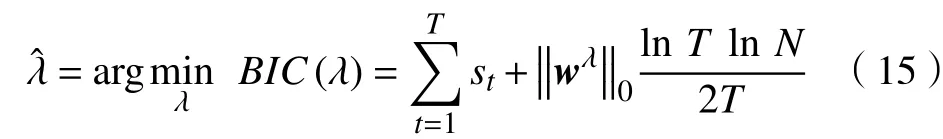
3.3 结果分析

现给出其他维数规模的模拟数据实验结果，仍然用式（15）的三因子模型生成模拟数据，情景维数T分别为1000，5000和10000，资产维数N分别为50和100，给出了3个置信水平（α= 0.99,0.95, 0.90）下的计算结果。其中，总时间表示为求解3个置信水平下的最优模型所用的总时间。在实际操作中，资产池和数据的情景维度一般是保持不变的，因此，最优调和参数λ ˆ可事先设定（表2），亦无须变化，这缓解了必须求解多个逐渐变化的λ才可以确定模型优越性的压力。根据前文的分析，实验中利用的对偶模型，主要受资产池规模的影响，情景规模对对偶模型的求解效率影响不大。实验结果表明（表3第3列），随着情景规模的增加，对偶模型在求解效率上的优越性表现更明显。表3中，EWP（equal weight portfolio）指等权重组合策略。

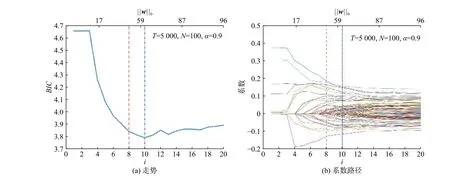
图2 BIC走势图与投资组合系数路径图Fig.2 BIC path and portfolio weights solution paths

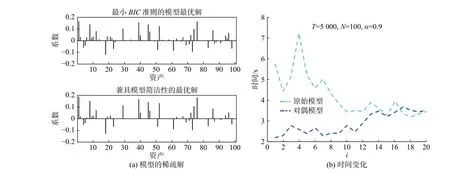
图3 模型的稀疏解和时间变化图Fig.3 Sparse weights solutions; Time paths for solving primal and dual model

3.4 真实数据

本文采用标普500高频交易数据作为真实数据进行了实验。资产池共有483个资产，情景维数为25805，（391条/d，共66 d）。由于高频交易数据本身的性质，价格变动幅度小，收益率量级普遍较小，在结果分析中，均将收益率转换为日收益率格式。

表2 最优模型对应的调和参数Tab.2 Tuning parameters corresponding to optimal models

3.5 结果分析

表4给出了在真实高频数据——大规模情景数据上的实验结果。表4所用的参数同样遵循BIC准则下兼具模型简洁性的原则。相比于标准Min-CVaR模型，本文提出的对偶策略提高了求解效率，同时兼顾了稀疏性以利于同步筛选投资标的。稍微遗憾的是得到的CVaR比Min-CVaR大，尽管差别不大。这也可以从数学优化的角度解释，由表4可知Min-CVaR的最优解稀疏度非常小，因为Min-CVaR利用资产池里几乎所有标的资产构建投资组合，势必会得到更优的目标函数。因此，Min-CVaR不具有同步挑选标的资产的特性。本文原始模型的解具有稀疏性，兼顾了自动挑选标的的特性，同时利用对偶模型求解，数倍地节省了原有模型的求解时间。

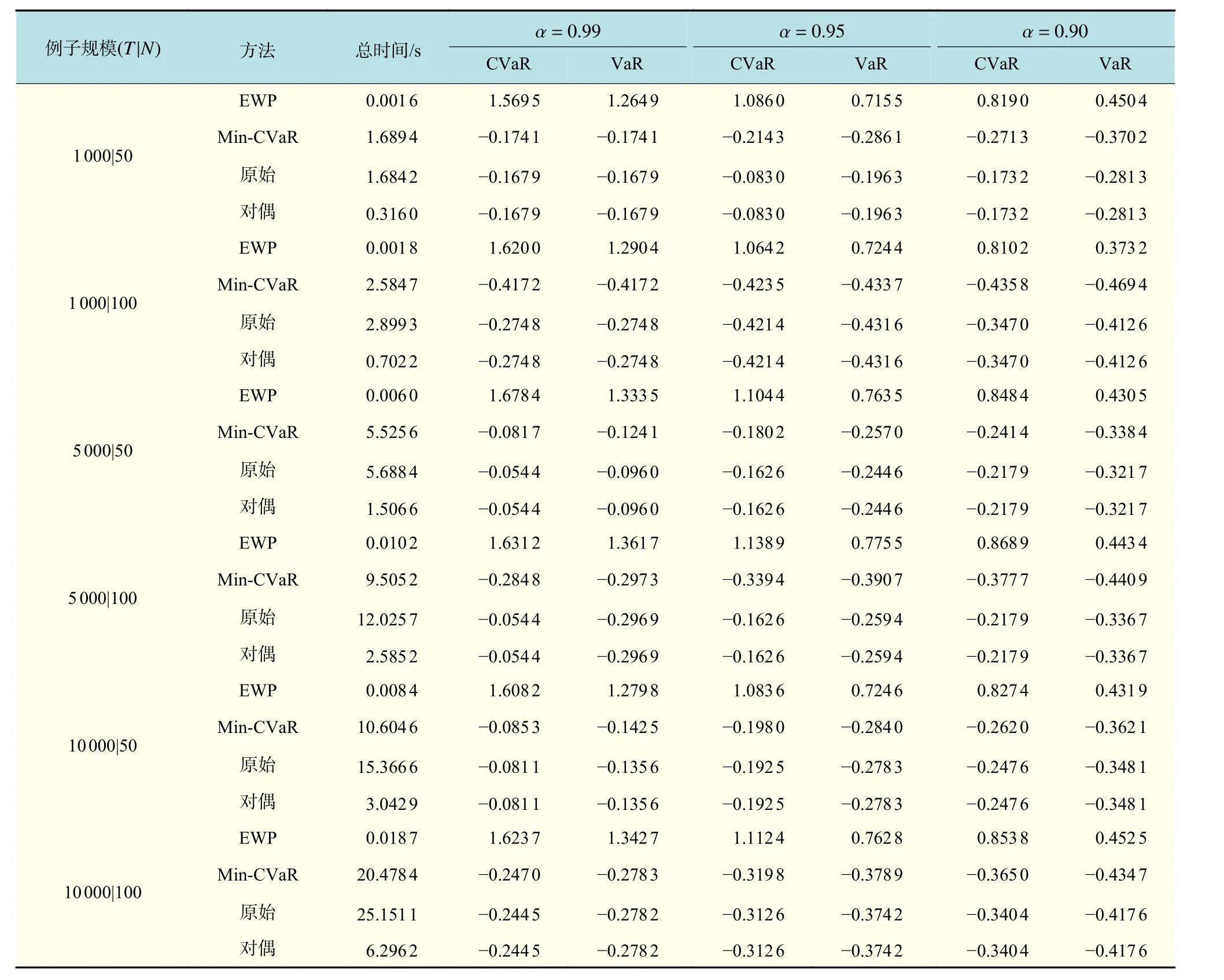
表3 在模拟算例上的表现Tab.3 Portfolio performance on a variety of simulation data cases

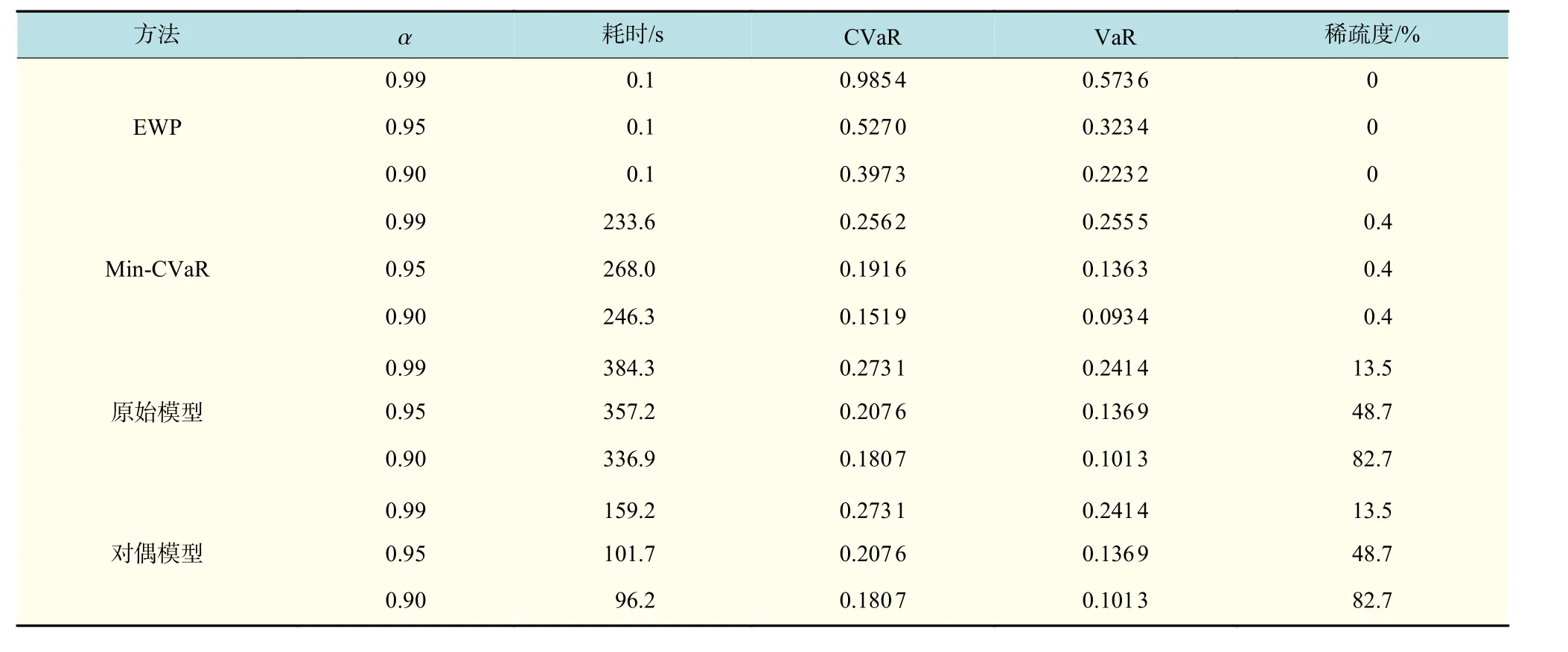
表4 在真实算例上的表现Tab.4 Portfolio performance on real-world data cases

表5给出了在真实数据上，不同概率下稀疏Min-CVaR模型所确定的两个调和参数，其中最小BIC准则的模型对应的调和参数为1，最小BIC的基础上，为了使模型更加精简，遵循一个标准差内最简洁原则确定的模型调和参数为2。观察可知2比1更大，根据前述分析，越大的调和参数将导致越稀疏的解。观察表5和图4均可发现，较大的调和参数2对应的模型的解具有更高的稀疏度，而相比于1，它们对应的风险度量（分别参考表5中VaR与CVaR值）相差并不明显。

表5 最小BIC准则对应的调和参数与兼具模型简洁性的调和参数Tab.5 Tuning parameters corresponding to minimum BIC and the ones with model simplicity

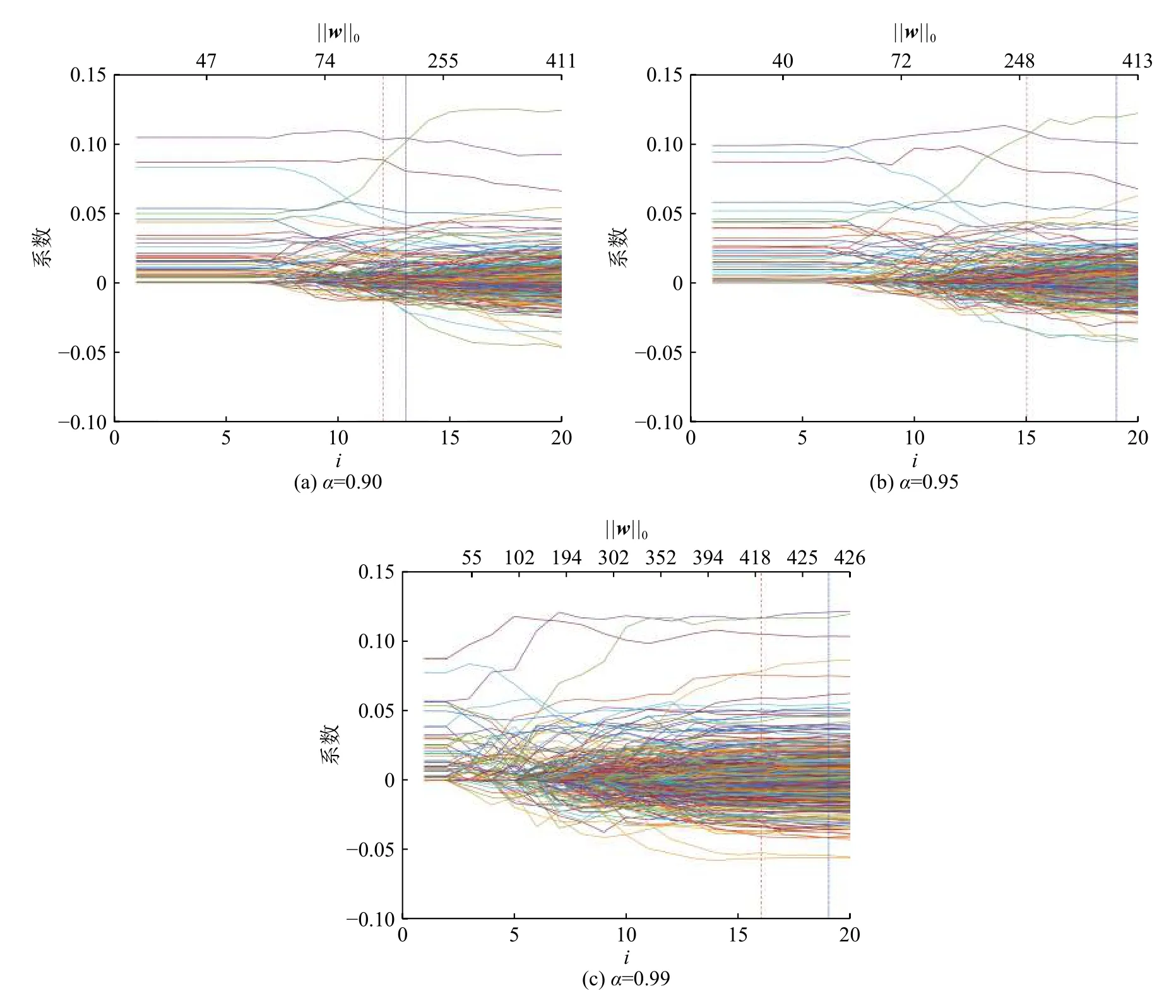
图4 权重路径图Fig.4 Portfolio weights solution paths

4 结 论

本文研究了大规模情景数据背景下的L1范数稀疏Min-CVaR投资组合模型。L1范数稀疏Min-CVaR模型可以同步完成从资产池中挑选标的资产和确定各标的资产配资比例的工作，且避免极端配资的情况，但此模型求解复杂性较高。本文通过对原始模型进行变换，得到对偶模型，利用单纯形法求解对偶模型得到最优解继而求得原始模型的最优解。本文对对偶模型和原始模型求解效率差异的理论原因进行了分析和解释，同时通过数值试验证实了求解对偶模型的策略在时间上的优越性。在计算大规模数据时，情景维数越大，效率提升的效果越显著。