基于极限过程学习机的储层微观孔隙结构识别

张强，王颖，郭玉洁

（东北石油大学 计算机与信息技术学院，大庆 163318）

油藏开发过程中储层的微观孔隙结构特征是影响储集层流体的储集能力和高效开发油气资源的主要因素，特别是油田进入高含水开采期间，准确分析和确定开采储层的微观孔隙结构特征是提升目的油层产能和提高采收率的关键。目前储层的微观孔隙结构识别主要采用室内实验法和测井资料法。蔺景龙等人［1］通过三层BP网络建立测井资料与微观孔隙结构类型的映射关系来识别油层的孔隙结构类型。Yakov等人［2］提出横向弛豫时间和毛管压力间的转换关系，为利用核磁共振测井资料研究储层微观孔隙结构提供了理论支持。肖飞等人［3］运用T2几何均值拟合法和伪毛管压力曲线转换法连续、定量地表征了储层微观孔隙结构。

2004年 Guang-Bin Huang等人［4］提出极限学习机（Extreme Learning Machine，ELM），具有调节参数少、网络权值随机化、学习速度快的优点。近年来针对ELM的研究也层出不穷，主要包括网络权值随机参数优化［5］、核函数ELM网络模型［6］，在线极限学习机模型［7］，网络隐层结构优化［8］及模型应用研究［9-11］等方面。尽管 ELM 在理论研究和具体应用上取得了丰富的研究成果，但基本ELM没能体现时间累积效应和延时特性。而在实际应用中很多系统的输入往往是与时间有关的，系统的输出依赖于对时间的累积和对空间的聚合。因此本文提出一种具有过程式输入的极限过程学习机模型（Extreme Pro⁃cess Learning Machine，EPLM）及学习算法，并将其应用于储层微观孔隙结构类型识别。

1 极限过程学习机原理

在极限过程学习机网络模型中，网络隐层由过程神经元组成，过程神经元有一个对于时间效应的累积算子，使其聚合运算可同时表达时变输入信号的空间聚合作用和对时间效应的累积过程。输出层为非时变神经元，相同类型的神经元执行相同的聚合/累积运算，理论和学习方法相同。极限过程学习机网络拓扑结构如图1所示。

图1 极限过程学习机网络模型

如图1模型所示，x1(t),x2(t),...,xn(t)为时变输入函数，wij(t)是输入层与网络隐层的连接权函数，θ(j1)是隐层神经元j的阈值，f为激励函数，vj是隐层第j个神经元与输出层的连接权值。极限过程学习机网络输入与输出的映射关系如下：

由公式（1）可知，极限过程学习机网络先对输入的时变信号进行时间加权累积，再进行这些时间累积效应的空间聚合，最后通过激励函数f的计算输出结果。

设极限过程学习机网络的输入为X(t)=(x1(t),x2(t),...,xn(t))，b1(t),b2(t),...,bl(t)为C[0,T]中的一组标准正交基函数，在一定的条件下可表示为基函数展开的级数形式：

同时连接权函数wij(t)也可用b1(t),b2(t),...，bL(t)基函数来表示，即：

由于b1(t),b2(t),...,bL(t)为[0,T]区间上的一组标准正交基函数，满足：

所以公式（4）可简化为：

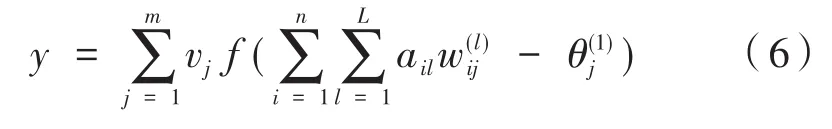
对于模型的学习问题，依据极限学习机学习算法原理，正交基展开后的系数和阈值随机产生。对于模型训练样本中的第k个样本输入(xk1(t),xk2(t),...,xkn(t),ok)，根据正交基展开的L个展开系数为，由此可以得出EPLM网络隐层的输出矩阵为：

采用广义逆计算隐层过程神经元与输出神经元之间的连接权值vj，公式为V=，其 中(HK×m)+=(HTH)-1HT，O=[o1,o2,...,oK]TK×1为网络输出。由上面的模型推导过程可以看出，网络结构和正交基展开项系数以及广义逆的求解方法是影响网络模型学习速度和预测精度的主要原因，故本文提出一种新的极限过程学习机训练方法。

2 基于改进混洗蛙跳算法的极限过程学习机训练方法

在一些实际应用中，与梯度下降的优化方法相比，ELM可能需要更多的隐层神经元。隐层神经元的多少也会导致过拟合或欠拟合问题，可能会产生非最优的权值，降低了算法的性能。另外，这种随机赋值使得ELM对未知测试数据的响应速度降低，隐层神经元个数越多，说明网络结构越复杂，易造成计算复杂度的增加和内存消耗等问题。从构建的极限过程学习机模型可知，网络输入相对于经典ELM要多，所以本文利用基于灰狼优化的改进混洗蛙跳算法找出更紧凑的网络结构及最优参数或近似最优参数，用基于张量乘积矩阵的广义逆求解算法加速模型参数求解。

2.1 基于灰狼优化的改进混洗蛙跳算法原理

经典混洗蛙跳算法首先对青蛙种群（共P个青蛙）依据适应值的大小降序排列，再把P个青蛙分成m个子群，每个子群含有n个青蛙（P=m×n）。在每次迭代过程中，每个子群中的适应值最优的青蛙定义为Xb，最差的青蛙定义为Xw，整个种群的最优青蛙定义为Xg，对最差青蛙按式（7）和式（8）进行更新：

位移的偏移量：

青蛙的新位置：

式中，rand()代表[0,1]之间的随机数，寻优步骤如下：

（1）如果通过式（7）、式（8）能产生更优解，则用其代替Xw；

（2）如果第1步产生的解没有得到改善，则用Xg替换Xb，继续采用式（7）、式（8）产生新个体；

（3）如果该新个体的适应值优于Xw，则替换，否则随机生成一个新个体代替Xw青蛙。

在求解高维复杂的优化问题时，若当前最优解是一个局部最优解，那么利用这个局部最优解来指导整个群体的学习，就容易陷入局部最优，较难达到所要的求解效果。这里提出一种基于灰狼优化算法的混洗蛙跳改进算法（Shuffle Leapfrog Algorithm Based On Grey Wolf Optimiza⁃tion，SFLAGWO）。

灰狼优化算法的优化原理取自于灰狼群体严格的等级机制和狩猎方式。灰狼群体的捕食行动由头狼领导，其它狼的任务是围攻，包括追逐、包围、骚扰和攻击。这种高效捕杀猎物的过程使得它们可以抓获更多猎物，具体实现方法如下：

式中，t表示当前迭代次数；A和C是系数向量；Xp是食物的位置向量；X是青蛙的位置向量。

其中，a是随着迭代次数从2线性递减到0；r1和r2在［0，1］范围内随机取值。

本文借助这个原理对青蛙子群中的个体向Xg学习的方式，改进成同时向Xg和Xb学习的方式，因为它们是整个种群中的最佳解，所以在SFLAGWO中假设Xg和Xb对全局位置有很好的了解。

2.2 基于张量积矩阵的广义逆求解方法

利用奇异值分解方法进行广义逆的计算速度是最快的，被广泛应用到极限学习机的训练中。但奇异值分解方法在大规模矩阵运算中需要大量的计算资源。文献［12］提出一种MOORE-PENROSE逆矩阵的快速计算方法，原理如下：

假设{e1,…,en} 和{f1,…,fn} 是 ℝk两组线性无关正交向量的集合，对于每个x∈ℝk有如下映射：

对于每一个n阶算子T都能被写成这种形式 ：，那么T就被称为向量组{e1,…,en} 和{f1,…,fn}的张量积，那么T的联合算子T*表示如下：

为了描述这种表示形式，选取{e1,…,en} 表示ℝk的标准基的前n个向量，假设fi具有如下形式：fi=(fi1,fi2,…,fik),i= 1,2,…,n那么，将fi作为列向量的矩阵T表示如下：

将该矩阵T称为给定向量集合的张量乘积矩阵。

定理1假设H为希泊尔特空间，若T=是一个n阶算子，那么它的广义逆也是n阶算子，对于每个x∈H都有以下定义：

其中，函数λi是n·n线性系统的解。

最后一个公式关系导致n·n线性系统如下所示：

上述系统的行列式是线性独立向量f1,…,fn的行列式，因此对于每个x∈H，它都有一个唯一解，其中未知数是函数λi，i=1,2,…,n。因此，为了确定张量乘积矩阵的广义逆，必须计算其展开时对应的λi：

综上所述，可以得出广义逆T+的计算方法如下：先计算线性独立向量的相应格拉姆矩阵，然后求解定义的n·n线性系统。对于每个j=1,…,n，运 用的λi(ej)来确定给定张量乘积矩阵T的广义逆。特别地，对于每个j=1,2,…,n，有λ1(ej),λ2(ej),…,λn(ej)作 为 相 应 线性系统的解。因此，广义逆T+具有以下形式：

假设矩阵T是n阶算子的矩阵表示形式，那么T就是一个k·k的矩阵，该矩阵前n列由k维空间上的线性无关向量组成ℝk，k＜n，其它列均由零组成。

2.3 极限过程学习机训练算法流程

（1）随机生成初始解，每个解由一组输入权重值、阈值和隐层节点数构成，其中输入权重值和阈值的范围均在［-1，1］区间，隐层节点数在整数区间取值；

（2）利用SFLAGWO算法对解空间的个体进行优化，找到最优的网络结构、网络权值和阈值；

（3）对于每一个解，利用2.2的方法求解极限过程学习机模型的广义逆，将分类精度作为模型的评估标准；

（4）当满足所寻优结果精度达到要求或是算法达到迭代次数，则算法停止，输出最优网络结构和权值，否则执行步骤（2）。

3 仿真实验

3.1 改进混洗蛙跳算法性能对比

将本文 SFLAGWO 算法与 SFLA、MSFLA［13］、MSFLA1［14］、ISFLA［15］和 MSFLA2［16］进行优化性能对比。实验环境为：Windows10操作系统，Intel酷睿i7处理器，Matlab R2014a。针对6个函数极值求解问题，各算法的参数设置如下：SFLAG⁃WO、SFLA、MSFLA、MSFLA1、MSFLA2和ISFLA的种群个数均设置为P=100，分组个数为10，子群内个体数为10。其中MSFLA的加速因子C值从1.0线性增加到2.5，MSFLA1的参数设置为2.1，ISFLA的参数C1=1.9，C2=1.8。每个算法分别计算20次取平均值。测试函数如表1所示，每种算法分别对6个函数的500维进行优化对比，测试结果如图2-图7所示。

从迭代对比曲线可知，本文所提的SFLAGWO的寻优效果最好，即使在维数为500的时候，寻优效果明显优于其他对比算法，并且对于f2和f5都找到了全局最优解。而且在迭代30次以内就能获得理想的效果，这表明所提算法在高维函数优化过程中寻优速度和精度都较好，因此对于本文所提极限过程学习机的训练具有很好的适用性。

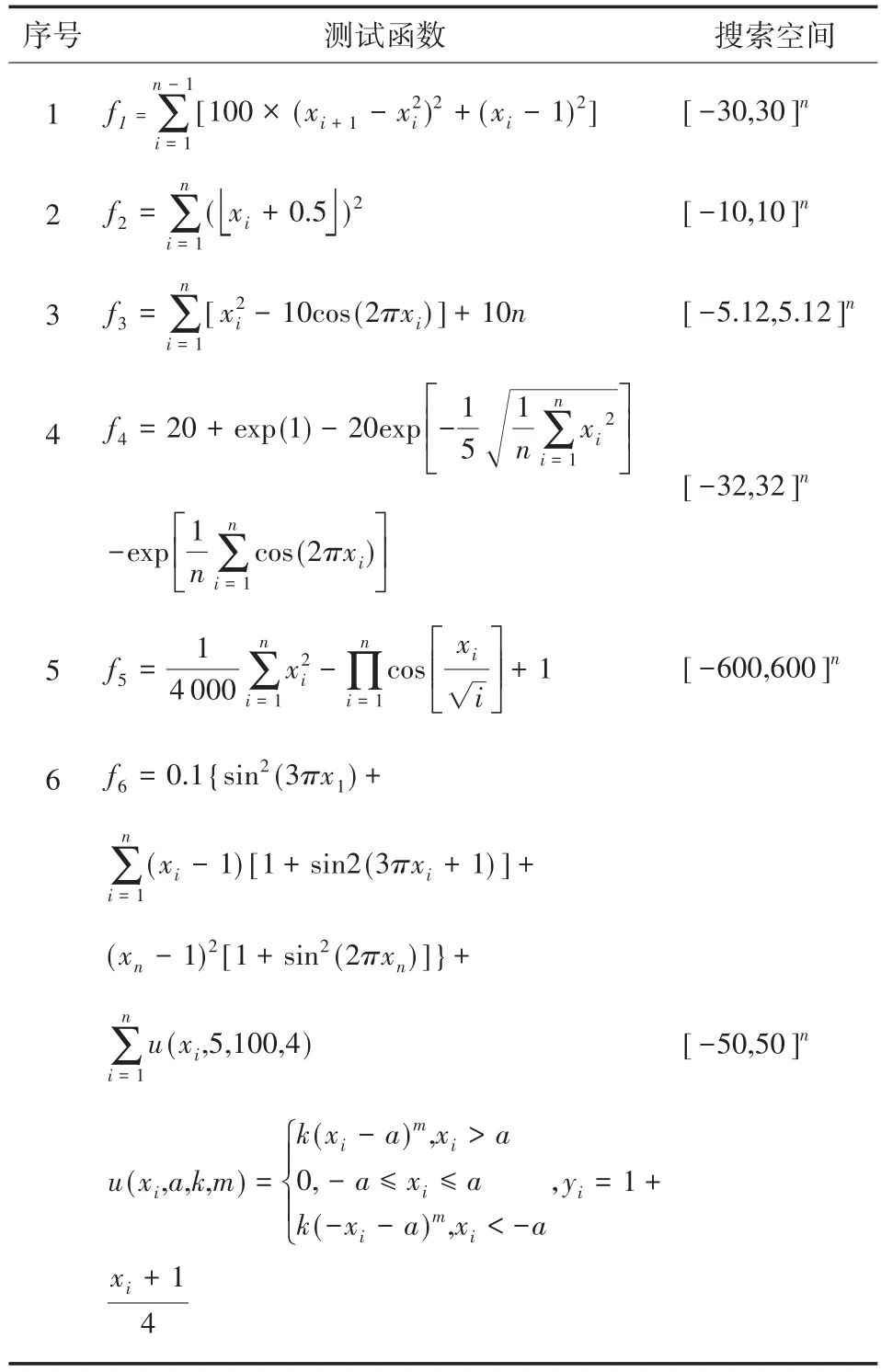
表1 优化测试函数

3.2 储层微观孔隙结构类型识别

储层微观孔隙结构类型识别对比实验选取自然电位、微梯度、微电位、2.5米电阻率、浅侧向、深侧向、自然伽马和补偿声波八条测井曲线作为所提网络模型的输入，设定储层微观孔隙结构类型为 1、2、3、4、5作为网络输出。采用350个测井数据样本组成训练样本集，50个测井数据样本组成测试样本集，对比基于BP学习算法的 PNN（BP-PNN）、基于 SFLA、MSFLA、MSF⁃LA1、MSFLA2和ISFLA学习算法的EPLM和基于本文算法和张量积矩阵（Tensor-Product Matrix）的学习算法（SFLAGWO-TPM-EPLM）的识别效果。极限过程学习机结构选择为8-m-1，即8个输入节点；隐层m个过程神经元节点，1个非时变一般神经元；其中隐层节点区间m=[16，64]，算法优化后的最优隐层节点数为56；其他学习算法的网络隐层节点数统一设置为64，基函数选择Walsh函数，当展开项数L=16时满足拟合精度要求，误差精度ε=0.5，每种学习算法运行20次，优化对比结果（相关系数R、平均绝对误差MAE、平均相对误差MRE、均方根误差RMSE、训练时间Time）如表2所示。

图2 函数f1迭代对比曲线

图3 函数f2迭代对比曲线

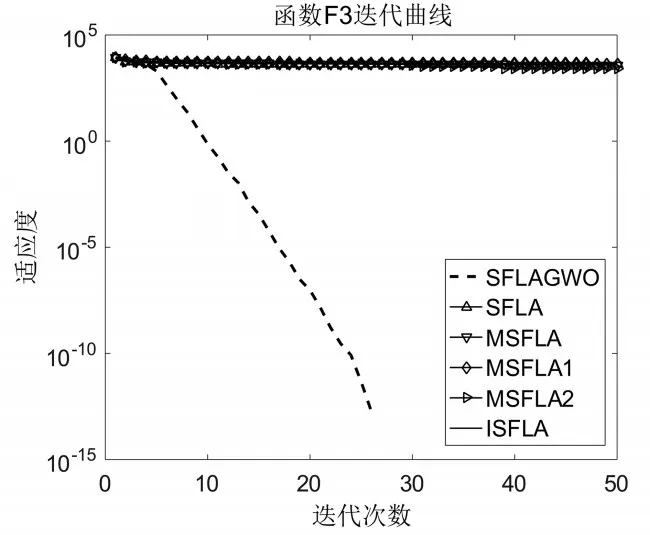
图4 函数f3迭代对比曲线

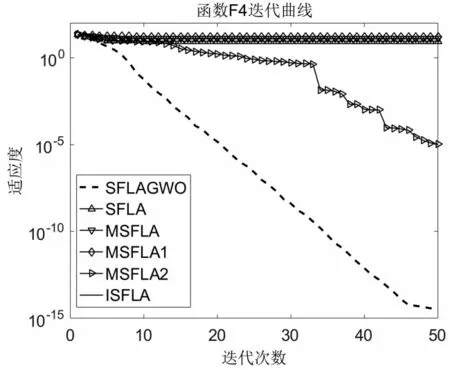
图5 函数f4迭代对比曲线

图6 函数f5迭代对比曲线

图7 函数f6迭代对比曲线

表2 七种算法训练结果对比

用七种算法训练得到的网络结构对训练样本和测试样本进行判别，对比结果如表3所示。

从实验结果可以看出：从训练耗时和识别结果上来看，BP-PNN耗时最多，SFLAGWO-TPMEPLM最好，这是因为BP算法需要计算梯度信息，且由于梯度下降法的早熟等问题而无法稳定的提供准确判别，SFLAGWO-TPM–EPLM最快，分析其原因是因为文中所提的SFLAGWO在向全局最优解学习的过程中，也参照组内最优解，利用追逐、包围、骚扰和攻击的方式加速了算法寻优性能，并且在高维函数寻优过程中能用较少的迭代次数获取理想的结果，同时采用新的广义逆矩阵求解算法改善了极限学习训练的速度和精度，二者的结合有效的强化了极限过程学习机的网络结构和权值。从而加强了模型对样本数据的识别率。

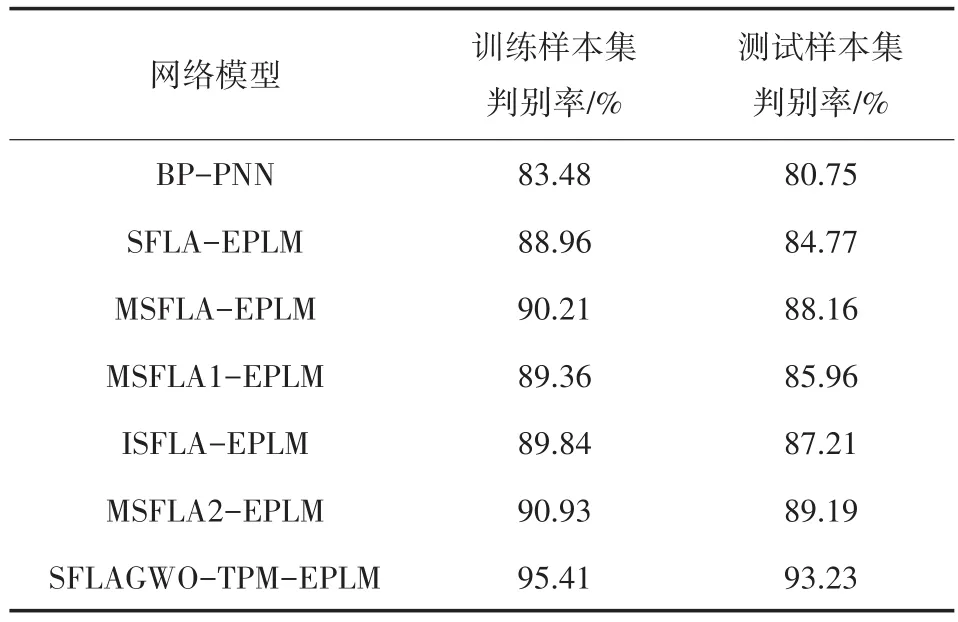
表3 判别结果对比

4 结论

本文建立一种具有过程式输入的极限过程学习机，提出基于SFLAGWO算法优化网络隐层节点个数及网络权值，并采用基于张量积矩阵的广义逆求解方法加快模型运算的速度及精度，实验结果表明无论是在高维函数优化还是储层微观孔隙结构类型识别的应用上，本文所提的方法都取得很好的效果，也为具有过程式输入的实际应用提供了一种解决方法，具有一定的推广价值。