D2D中基于风驱动的功率控制算法研究

白宇，郎百和，王冰鑫

（长春理工大学 电子信息工程学院，长春 130022）

随着各种智能终端数量爆炸性的增长以及大数据、云计算、物联网等新兴互联网技术的大规模发展和覆盖，传统蜂窝网络中匮乏的频谱资源无法满足用户需求，终端直通通信（Deviceto-Device，D2D）应运而生，它允许两个临近的用户不经过基站直接通信，这种技术能够改善现有蜂窝网络的通信质量，提高频谱利用率，具有潜在的提高系统性能和提升用户体验的前景，从而受到研究人员的广泛关注［1］。

D2D通信提供了更方便、更灵活且更高效的传输模式，但随之而产生的由于资源复用带来的同频干扰问题，不仅会影响各用户满意度，同时也会给整个系统的稳定性带来考验。因此，如何合理的分配资源［2］、配置D2D用户及蜂窝用户的发射功率［3］、保证用户服务质量（Quality of Service，Qos）来优化吞吐量［4］、功耗、能效等系统指标成为D2D通信的关键问题和研究热点。

对于上述问题及优化指标，本文重点针对功率控制及资源分配开展研究。Doppler等人［5］在保证蜂窝优先通信的基础上，分析了在不同约束条件下，如发射功率限制和能效限制等的系统吞吐量表现。陶静，朱琦［6］在NOMA条件下（Non-Orthogonal Multiple Access），采用 KM 算法为D2D用户分配信道，然后运用KKT最优约束条件导出功率分配方案，在保证蜂窝用户服务质量的前提下最大化了总能量效率。Asmaa Abdallah等人［7］提出了一种分布式功率控制方案，并对其采用基于随机几何的数学工具进行建模，通过使用D2D链路和基站的距离相关的路径损耗参数（包括估计误差裕度）来补偿大规模路径损耗效应，提高了D2D用户覆盖率。

目前，也有很多研究人员受启发式算法的影响，将各种仿生算法引入到D2D通信中，Chengcheng Yang［8］将遗传算法应用于资源分配问题中，首先通过在D2D用户和蜂窝用户发射功率可行区间内搜索最优功率分配，再利用遗传算法在整个网络范围内获得近似最优匹配为用户分配频谱资源，虽然提高了吞吐量，但算法复杂度较高。

Mengmeng Ru［9］在文献［8］的基础上，将频谱资源分配问题与功率分配问题转化成混合整数非线性规划问题（Mixed Integer Nonlinear Program⁃ming，MINLP），提出一种混沌遗传算法与图着色法相结合的方式，优化了系统容量，同时也降低了算法复杂度。

对于粒子群算法的应用，刘辉、夏威等人［10］在所提算法中，先为D2D用户分配频谱资源，再对D2D和蜂窝用户的发射功率采用粒子群算法寻优，在保证了用户公平性的基础上，提升了系统吞吐量。Jun Xu等人［11］将资源分配与功率分配建模为一个联合问题，分别用二进制粒子群算法及标准粒子群算法解决上述所形成的MIN⁃LP问题，大大提升了系统吞吐量。然而上述文献中所应用的启发式算法易陷入局部最优，且个别算法复杂度过高。因此针对上述缺陷，本文对资源分配和功率配置两个问题，采用两步解决的方式，首先应用匈牙利算法将信道分配问题转化为0-1最优指派问题，得到信道分配方案，然后，将风驱动算法［12-13］应用于D2D用户及蜂窝用户发射功率的调整，以提升系统整体吞吐量。

1 系统模型

本文考虑单小区单基站蜂窝网络环境下，采用underlay工作模式，D2D用户通信复用蜂窝上行链路频谱资源，以基站Bs为圆心，半径为R=500 m的圆内，涵盖着N个蜂窝用户，M个D2D用户，且M≤N。其中，所有用户分布在Bs半径25 m以外以保证通讯能够建立，蜂窝用户CUE和D2D发射端D2DT在小区内随机生成，D2D接收端D2DR以对应的D2D发射端为圆心半径r=25 m内随机生成以保证D2D用户间可以正常通信。为避免干扰过大可能引起的通信中断［14］，规定每条蜂窝信道只能被一对D2D复用，每对D2D也只能复用一条信道。另假定基站可以预先通过上行链路获得信道状态信息（Channel State Information，CSI）。

图1 D2D通信及干扰示意图

D2D用户复用小区中蜂窝用户资源时会产生同频干扰，如图1所示，D2D发射端D2DT1与D2D接收端D2DR1构成一对D2D用户，并复用蜂窝用户CUE1上行链路资源，此时，D2DT1会在基站处产生干扰，同时CUE1会对D2D用户接收端D2DR1产生干扰。于是蜂窝用户CUEi在基站处的信干噪比（Signal to Interference plus Noise Ra⁃tio，SINR）为：

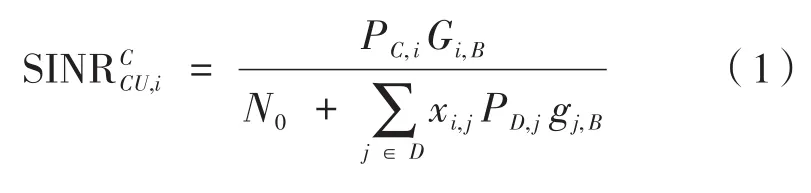
式中，PC,i表示蜂窝用户i的发射功率；N0表示在接收端所收到的噪声；PD,j表示第j个D2D用户发射端的发射功率。另外，本文中另设G表示用户与基站的信道增益，g表示用户与用户之间的信道增益。因此在上式中，Gi,B表示蜂窝用户i与基站Bs的信道增益，gj,B表示第j对D2D的发射端与基站Bs之间的信道增益。xi,j定义为信道资源复用因子，其取值为0或1，用来指示信道的一对一复用，即：

信道增益G或g表示式如下：

式中，pathloss表示链路收发端的路径损耗；shad⁃owfade表示阴影衰落。第j对D2D接收端处的信干噪比为：

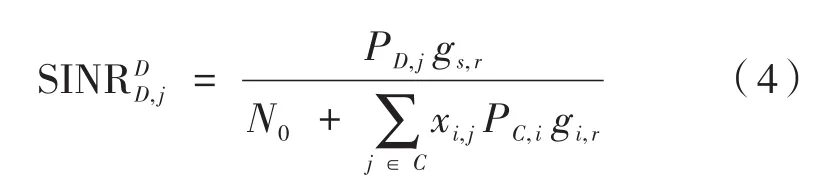
式中，gs,r与gi,r分别表示D2D对间发射端与接收端的信道增益和蜂窝用户i与复用其链路通信的D2D用户接收端信道增益。

由香农定理可推得，当D2D对j复用蜂窝用户i时，二者吞吐量分别为：

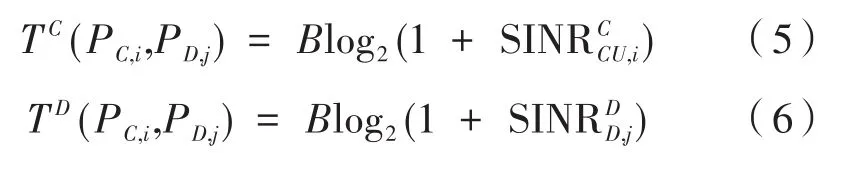
式中，TC和TD分别代表共用资源的蜂窝用户和D2D用户的吞吐量；B为链路带宽。则系统总吞吐量表示如下：

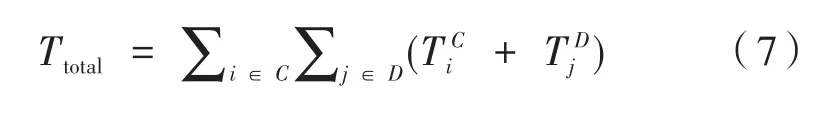
基于上述公式，以系统总吞吐量最大为目标的问题可以转化为如下优化问题：

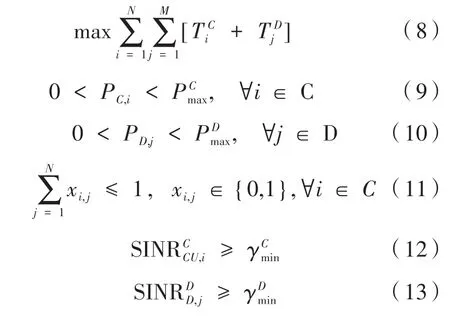
约束条件（9）、（10）限制蜂窝用户和D2D用户的发射功率不能超过各自的发射功率最大值。式（11）保证了每对 D2D 用户只能复用一条蜂窝信道，且不同D2D对不能复用同一蜂窝信道，以确保系统干扰可控。式（12）和式（13）要求蜂窝用户和D2D用户的信干噪比应大于对应的SINR阈值和来保证用户的QoS。

基于上述分析，带限制条件的系统总吞吐量最大的优化问题为混合整数非线性优化问题（MINLP）。这一类问题很难实现全局最优，是一种NP-Hard问题，相对于传统解决方案，应用启发式算法解决此类问题有其天然的优势，如全局搜索能力强，速度快等优点。本文先应用基于在整个系统中蜂窝用户与复用其信道的D2D对平均距离最大的匈牙利算法解决资源分配问题，再应用风驱动算法对蜂窝用户及D2D用户的发射功率进行优化，以达到对系统总体吞吐量的优化。

2 资源分配算法

匈牙利算法最初是由匈牙利数学家D.Konig所提出的定理，其在该定理中证明了“矩阵中独立0元素的最多个数等于能覆盖所有0元素”。后来由W.W.Kuhn在求解0-1指派问题时引用该结论并改进，仍称为“匈牙利算法”。所谓0-1指派问题，即指派M个个体完成N项任务使效率最大化。延伸到本文的资源分配问题，即为M对D2D分配N个蜂窝信道，以期降低由于引入D2D给系统带来的干扰。由此本文提出一种基于匈牙利算法的资源分配优化方案，即基于所有D2D用户到蜂窝用户平均距离最大的配对原则进行资源分配。

首先遍历得到系统中每对D2D到每个CUE的通信距离矩阵D=di,j，其中D为N×M维矩阵，di,j表示第j对D2D的接收端到第i个蜂窝用户的距离。再令S=si,j表示资源复用指示矩阵，且同为N×M维矩阵，其中si,j含义如下：

因此本文中基于所有D2D用户到蜂窝用户平均距离最大的资源分配算法转化为如下优化问题：

考虑到匈牙利算法的应用条件，要求效率矩阵中所有元素为正且优化方向为极小，因此上述模型改写为：

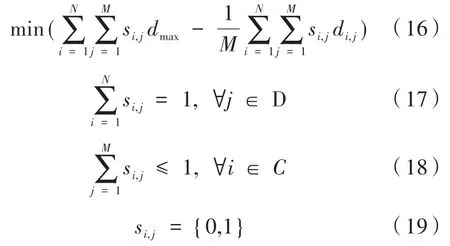
上述限制条件中式（17）、式（18）、式（19）保证了系统中D2D对与蜂窝用户的匹配关系是一对一的，且不同D2D用户对不允许复用同一条蜂窝信道。对上述模型应用匈牙利算法，即将基于所有D2D用户到蜂窝用户平均距离最大的配对问题转化为对资源复用指示矩阵的0-1指派问题，得出最优资源复用策略。匈牙利具体算法步骤如下：

（1）先将效率矩阵中每行元素减去对应行的最小元素，再将得到的矩阵每列减去对应列的最小元素，使每行每列都出现0元素，生成矩阵E1。若M＜N，则将效率矩阵添加（N-M）列，使效率矩阵行、列数相等再进行上述操作。

（2）用最少的直线数u覆盖步骤（1），得到矩阵中所有0元素，得到矩阵E2。

（3）判断若u=N，则停止运行，得到最优资源复用指示矩阵E2=si,j，若u＜N，则继续执行步骤（4）。

（4）当u＜N时，从矩阵E2中未被直线覆盖的数字中找到最小值w，再将未被覆盖的元素减去w，然后将直线交点处的元素加上w，剩余被直线覆盖的元素保持不变，得到矩阵E3。

（5）找出E3中所有独立0元素，并令其为1，其他元素置为0，得到一个仅含0、1元素的矩阵E4=si,j，最终得到资源复用指示矩阵si,j。

通过上述步骤得到的资源复用指示矩阵si,j等同于第一章中的xi,j，此处更换符号是为了更准确的说明算法应用。

3 基于风驱动的功率分配算法

在蜂窝系统中引入D2D通信势必会对整个系统产生干扰，传统的固定功率控制方案无法达到对系统干扰的控制，因此合理地对蜂窝用户发射功率Pc和D2D用户发射功率Pd进行灵活控制能有效的抑制干扰。本文应用风驱动算法对Pc、Pd进行联合控制。

风驱动算法是基于对大气中简化的空气质点受力运动模型模拟的一种迭代启发式算法，其最早由Bayraktar Z以及Wener D H博士等人提出，算法核心研究了空气质点在大气中主要受到摩擦力、重力、气压梯度力、科里奥利力的作用，应用牛顿第二定律结合理想气体状态公式，推导得出空气质点在迭代过程中的速度、位置更新方程，并结合压力值（即适应度值）对每次迭代中每个质点的位置优劣进行排序，从而得到全局最优值。

空气质点的速度更新公式为：

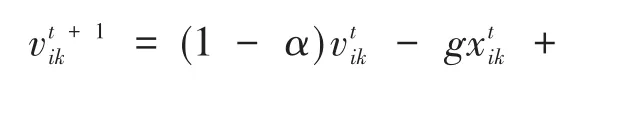
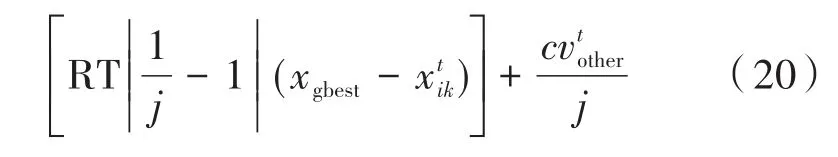
空气质点的位置更新公式为：

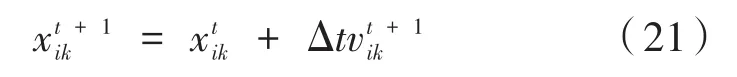
更新速度的边界条件限制如下：

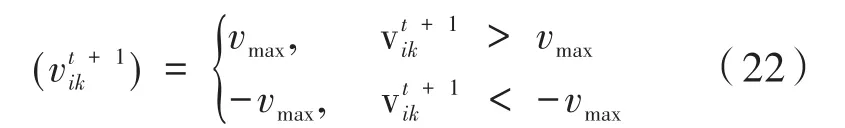
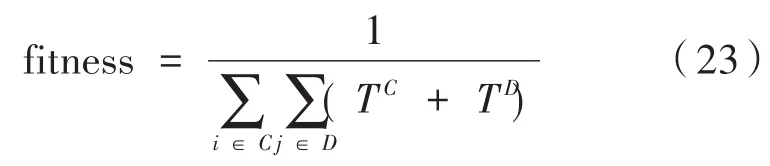
其中，TC和TD分别对应上文中的公式（5）和公式（6），fitness表示个体压力值，即适应度函数值。

风驱动优化算法流程图如图2所示。

因此，应用风驱动算法对Pc、Pd寻优的步骤如下：

（1）设置算法各个参数α、g、RT、c的值以及位置和速度的边界条件。

（2）初始化种群中各质点速度、位置即初始化蜂窝用户和D2D用户功率，在限制条件（9）及（10）允许范围内随机为Pc、Pd赋初值。

（3）根据公式（23）计算各质点压力值并按升序排列，记录当前种群最优值为xgbest。

（4）根据式（20）更新各质点速度并判断速度值是否越界，若越界，则置与速度边界。

（5）根据式（21）更新各质点位置并判断位置是否越界，若越界，则置于位置边界。

（6）计算更新后的各质点适应度值并排序，更新当前种群最优值xgbest。

（7）判断是否达到最大迭代次数，若达到最大迭代次数，算法结束，输出全局最优值xgbest，得到系统中总吞吐量，否则返回步骤（3）继续迭代。

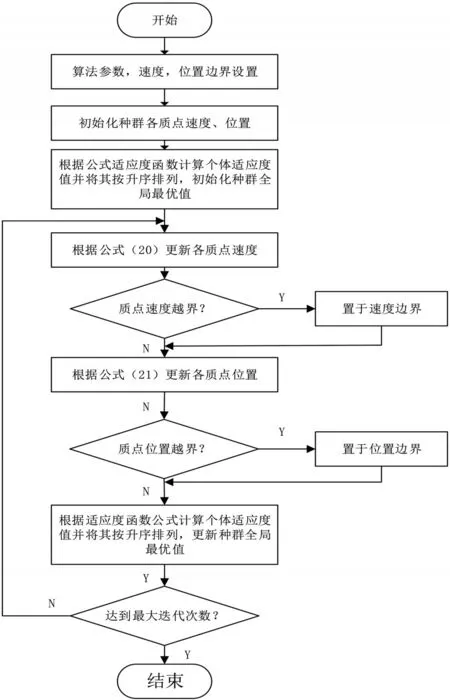
图2 风驱动算法流程图

4 性能仿真及分析

为了验证所提算法的优势及可行性，本文应用单小区单基站作为仿真场景，利用Matlab软件对所提算法进行仿真分析，为便于叙述，将本文所提算法记为HWDO，作为对比的随机接入算法记为Random、常规风驱动算法记为WDO。其中，风驱动算法中种群大小设置为20，迭代次数设置为500次，系数RT值设置为3，重力加速度常数g设置为0.2，α和常数c都设置为0.4，速度边界设置为0.3。其它仿真参数具体如表1所示。

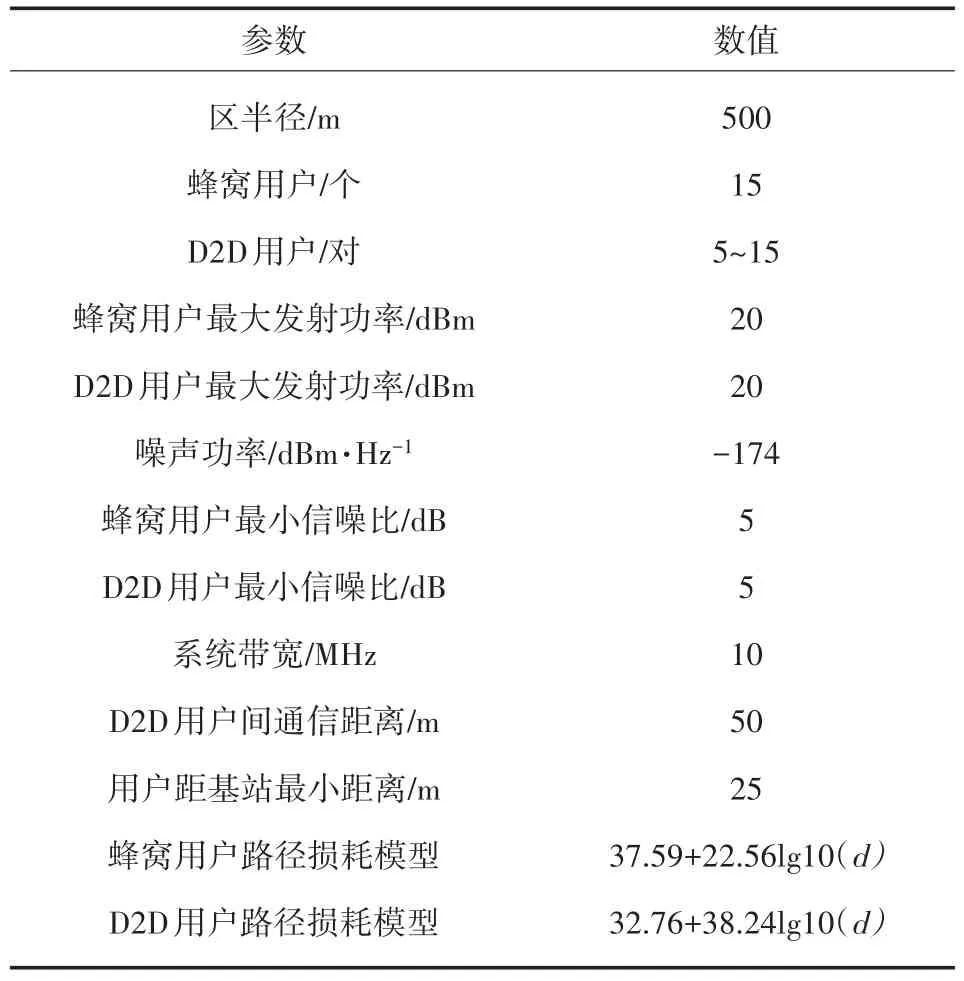
表1 其它仿真参数

表1给出了蜂窝小区系统各参数设置，仿真参数的设置基于表1中各参数数值，其中D2D用户对数5～15表示11组仿真数据。

如图3所示，本文对比了D2D用户对数从5增加到15时，不同方案对系统总吞吐量的优化表现，图中数据为50次仿真结果的均值。当系统中D2D用户数增多时，三种算法下的系统吞吐量都有所增加，但是增长速度随着D2D用户增多而趋于平缓，这是由于当系统中引入的D2D用户增加时，虽然系统总吞吐量有所提升，但由于同时引入了干扰且D2D用户的备选蜂窝信道减少，导致部分D2D用户与蜂窝用户的匹配灵活度下降，从而导致增长速度放缓。应用了常规WDO算法进行功率控制后，可以看出系统总吞吐量有明显提升，提升幅度在9%左右，而在其基础上应用的HWDO算法，即先用匈牙利算法优化信道，再对功率进行WDO算法寻优的方案在常规WDO算法基础上使系统吞吐量提升了约7%左右，显然优于前两种算法，因此相较于Random算法及WDO算法，HWDO算法有着更好的性能。

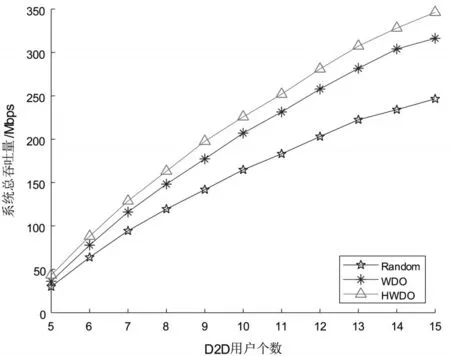
图3 三种方案下系统吞吐量随D2D用户数对比

图4 蜂窝用户平均SINR变化趋势

图4所示为三种不同方案下，蜂窝用户平均SINR值随着系统内D2D用户对增多的变化情况。考虑蜂窝用户的SINR在一定程度上可以代表蜂窝用户的QoS，SINR值越大，用户满意度越高。从图中看出，三种算法下的蜂窝用户SINR均值都有波动。其中，Random算法波动最大，且蜂窝用户SINR均值整体呈大幅下降趋势，且当D2D用户对增长到12个以上时，由于没有相应控制干扰的策略导致SINR平均值降到5以下，即无法正常通信。WDO算法下的蜂窝用户平均SINR值整体也呈下降趋势，但由于加入了功率控制策略使得干扰得到有效控制，蜂窝用户SINR均值要明显高于Random算法。由于HWDO算法在WDO算法基础上利用匈牙利算法事先为D2D用户分配信道，优化了D2D用户对与蜂窝用户的匹配，然后再利用WDO算法对Pc、Pd进行联合优化，使得整个系统通信环境得到大幅度改善，表现在结果图中则可以看出应用HWDO算法令整个系统中蜂窝用户平均SINR值要高于其他两种算法，且波动幅度也小于其他两种算法。

5 结论

对于在蜂窝小区引入D2D通信所带来的问题，本文应用匈牙利算法与风驱动算法结合来优化信道选择以及功率控制。在满足蜂窝用户QoS的基础上，结合预先得知的信道状态信息，先优化D2D用户对与蜂窝用户的匹配，再利用迭代启发式风驱动算法为蜂窝用户和D2D用户进行功率的动态调整。通过对比验证，仿真结果表明上述所提HWDO算法相较于Random算法及WDO算法系统吞吐量分别平均提升了16%和7%左右，并且HWDO算法的应用相比于其他两种算法使得蜂窝用户平均SINR稳定在较高水平，随D2D用户增加波动较小。综上，本文所提算法显著提升了系统吞吐量的同时，保证了蜂窝用户的通信质量。