经典试题的答案真的错了吗？<br/>——兼论理想化模型的建立问题

经典试题的答案真的错了吗？
——兼论理想化模型的建立问题

2021-01-26刘大明江秀梅

课程教学研究 2021年1期

文∣刘大明江秀梅

轻弹簧是一个典型的理想化对象模型，属于轻物模型之一。轻物模型的核心特征是忽略质量，从而与质量有关的其他属性(如重力、动能、动量等)也一并忽略了。在实际教学中，大多数教师都忽视了轻物模型的建立过程，其根本原因在两个方面: 已有的课程资源(如教材)缺乏物理模型思想；教师自身对物理模型的理解十分有限[1]。由于对理想化模型思维方法认识有限，面对理想化模型时极容易产生困惑。《轻弹簧弹性势能凭空消失的困惑引发的再反思——兼谈轻弹簧理想化模型的条件》[2]就一道经典试题的科学性提出了质疑，质疑“忽略弹簧质量”是一个不恰当的题设条件，继而否定了试题答案的正确性。实质上，《条件》从弹性势能凭空消失这一不符合科学事实的情景中否定了轻物模型的一个普遍特征。殊不知，《条件》正是对理想化模型存在认知缺陷而产生了认知困惑，最终对一道经典试题做出了个人认为不太适合的评价。本文继续以该经典试题点评分析为例，与《条件》作者和其他同仁一并探讨理想化模型的建立问题，以期通过更为广泛的讨论交流，为学科核心素养落地生根添砖加瓦。

一、经典试题经典性点评分析

【题目】如图1所示，一重物m悬挂在弹簧下，再用一细绳固定于天花板上，整个装置静止后，用火焰烧断细绳，在绳断开的瞬时，m的加速度为a，(忽略弹簧质量和空气阻力)则( )

图1

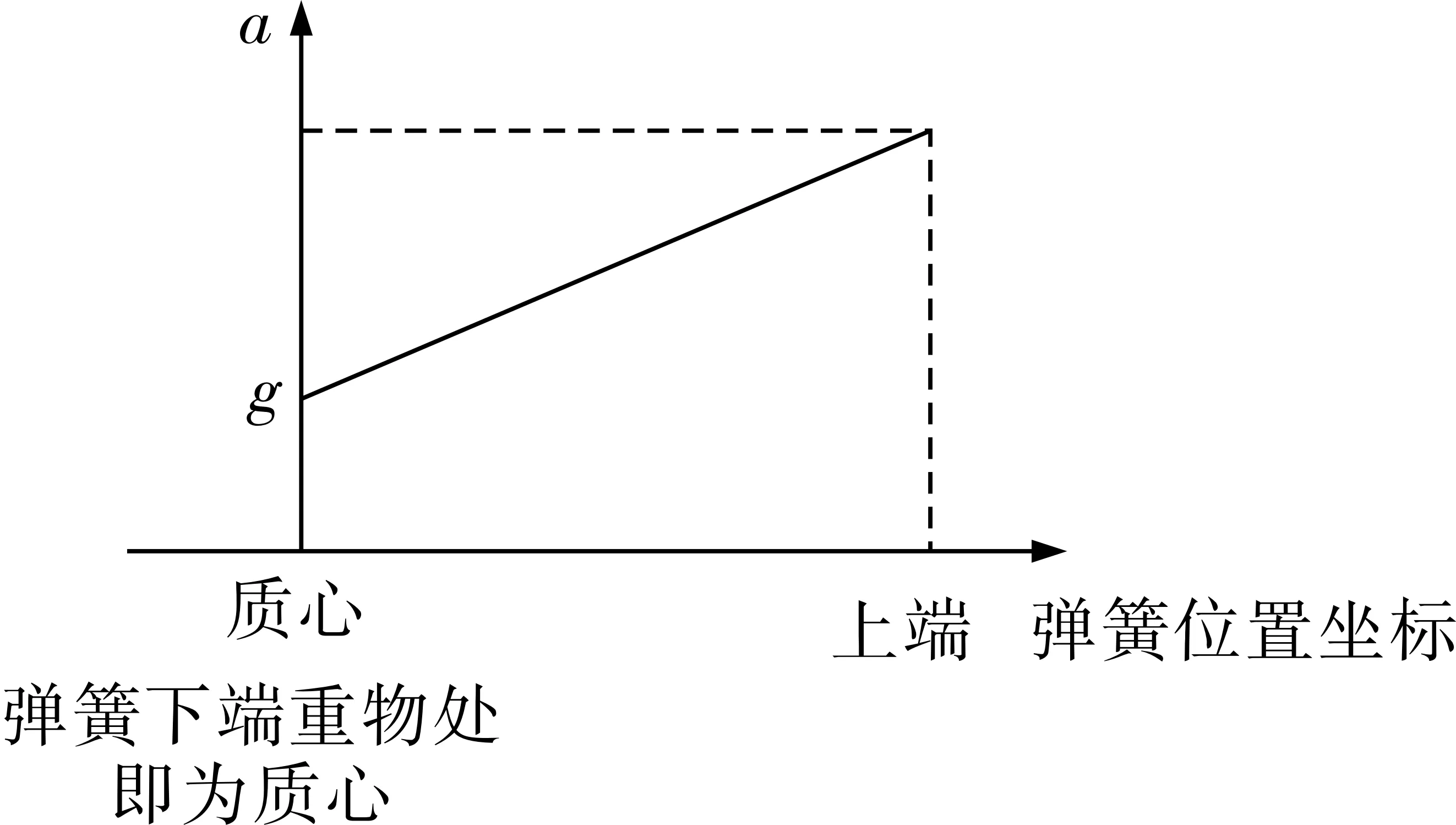
A.a

B.a=g，方向向下

C.a>g，方向向下

D.a

【答案】B

此题常见的解法有两种。

【解法1】由于轻弹簧质量忽略，绳断开瞬间，弹簧形变立即消失，弹力为零，所以重物只受重力作用，加速度为a=g，方向竖直向下。

【解法2】设轻弹簧上下两端分别受力为F1、F2，根据牛顿第二定律，对轻弹簧有F1-F2=m0a，由于轻弹簧的质量m0=0，则F1=F2，即轻弹簧两端的力总是相等。绳断开瞬间，轻弹簧上端没有物体，上端不受力，即F1=0，从而F2=0。再根据牛顿第三定律，重物也不受弹簧拉力，只受重力作用，故加速度为a=g，方向竖直向下。

【点评】两种解法在本质上是一样的，都运用了“忽略弹簧质量”条件，即轻弹簧模型的特点；只不过解法1更直接一些，而解法2给出了基于轻弹簧模型的解模分析，充满了科学推理的魅力。根据题设条件，推导相关结论，已经成为一种习惯性的“解题”思维了。当今物理高考试题，绝大多数都以“科学推理”素养为核心进行考查，故而形成前述习惯性解题思维似乎无可厚非。但从科学探究和实践运用而言，对所推导的结论进行反思、讨论、验证，最终确认假设条件的正确与否，是不可或缺的活动环节。就此意义来说，仅有解题思维是无法推动科学进步的，甚至可能在实践中犯下错误。

为了后续讨论方便，我们先提供一种非常规解法：

【解法3】绳断开瞬间，对轻弹簧和重物组成系统运用质心运动定理，因为系统只受重力作用，所以质心加速度为aC=g，方向竖直向下。由于轻弹簧质量忽略不计，质心就在重物上，所以a=aC=g，方向竖直向下。

【点评】解法3运用了大学物理中的质心运动定理，推理严密，逻辑严谨，非常具有说服力。对高中生而言，这一解法“超纲”了；但对于高中物理教师备课而言，充分体现了“站得高看得准”的优势，也彰显了“学生半桶水教师满桶水”的专业要求。

二、经典试题批判性点评分析

《条件》认为解法1、解法2逻辑推理是严密的，是无懈可击的。于是另辟蹊径，试图从能量角度对上述经典试题进行质疑批判。

如是就得出了一个违背能量守恒定律的结论：弹性势能凭空消失了。针对这个结论，《条件》提出了批判性解决办法，认为弹簧可视为轻弹簧模型必须满足两个条件：一是弹簧两端都要连接物体；二是弹簧要发生弹性形变。绳子断开瞬间，弹簧一端自由了，不满足上面条件一，故不能视为轻弹簧，经典试题题设“忽略弹簧质量”是一个不恰当的条件。如以“重弹簧”模型来分析，就能克服弹性势能凭空消失的问题。既然是重弹簧，质量就不可忽略，惯性就不能忽略，弹簧也就不会立即恢复原状，因此弹簧的弹性势能就不会凭空消失。继而，就重弹簧而言，弹簧上的力处处不相等，每个小环的运动状态不相同，绳断瞬间，弹簧的质心有所下移。运用质心运动定理，可知弹簧和重物的整体质心aC=g。然而，对重物而言，绳断瞬间，弹簧并没有立即恢复原状，重物受力还没有发生改变，所以重物的加速度a=0。就此，说明高考试题存在科学性错误。

但弹簧视为轻弹簧，必须满足两端约束吗？两端约束后存储了弹性势能，一旦一端自由，弹性势能的去向如何呢？我们从三个角度来分析论证。

三、对批判性评析的再批判

《条件》对经典试题提出的质疑批判，存在两处逻辑上的不足和缺憾。

(一)弹性势能突然消失不等于凭空消失

《条件》认为弹簧一端自由后，不管弹簧“质量多小”，都不能视为轻弹簧，唯有如此才能打消弹簧立即恢复原状，弹性势能凭空消失的困惑。事实上，弹簧立即恢复原状，只能说明弹性势能立即消失，不能说明弹性势能凭空消失。《条件》运用质心运动定理分析了质心的运动情况，与此同时也必将说明弹簧与重物的整体动能增加量是重力做功的结果，即等于整体重力势能的减少量。那么，弹簧最终恢复原状后，弹性势能去哪里了？似乎依然“凭空消失”了！也就说，《条件》提出的弹性势能凭空消失问题，作者只是疑惑，并没有解决这个问题。

(二)弹簧的质心不是弹簧与重物整体的质心

《条件》在论证中混淆了弹簧的质心和弹簧与重物整体的质心。运用质心运动定理得出了整体质心加速度aC=g，然后预设重物保持平衡结论的情况下，默认弹簧的质心加速度等于整体的质心加速度。如此论证，属于循环论证，不具说服力。与解法3比较可知，运用质心运动定理恰恰说明“忽略弹簧质量”是有意义的，也是恰当的，是经典试题的关键性条件。

对推导结论进行反思和讨论，继而对题设条件进行批判质疑是有意义的，但此思维活动一定要建立在更严密的理论论证和更具说服力的实验验证基础上。

四、实验理解轻弹簧模式

《条件》讨论的是线性弹簧，于是我们仅就此类弹簧做了下列实验。

【实验一】固定弹簧一端，拉伸弹簧另一端至适当长度后释放。使用硬弹簧做实验发现，弹簧迅速恢复原状，并发出碰撞响声；使用软弹簧做实验发现，弹簧迅速恢复原状，发出碰撞响声外，自由端还出现“甩尾”般的摇晃摆动现象。

实验一的实验现象说明：弹簧拉伸后自由释放一端，弹簧恢复原状过程中，弹性势能在弹簧内部碰撞中耗散了。也就是说，弹簧立即恢复原状，弹性势能并非凭空消失，而是耗散了。

【实验二】教师(体重70千克)站在体重计(家庭版，灵敏度不高)上，快速振动手指，体重计的示数均没有变化。

实验二的实验现象说明：从动力学视角而言，手指相比整个身体质量是可以忽略不计的，建构轻物模型具有理论价值，也具有实践意义。另外，振动手指过程中的能量转化并未影响动力学结论。由此类比，在“弹簧质量可以忽略”的前提下，弹性势能的转化未必会影响轻弹簧动力学特征——轻弹簧两端的力几乎相等。

【实验三】实验器材：灵敏电子台秤一个、固定了轻质软弹簧的重物(约320克)一个。实验组：如图2，提起弹簧自由端，使得对台秤的压力为零，然后自由端释放，发现台秤数字立即增至320克左右(在增长过程中，只能看到诸如16、180、318等非连续性示数，增长时间不超过0.4秒)，自由端摇晃摆动时，也是维持在320克左右(自由端摇晃停止时间超过2秒)；对照组：如图3所示，提起重物，使得对台秤的压力为零后释放，发现台秤数字立即增至320克，数字增长特点和时间与实验组几乎相同。

图2

图3

设计实验组，意在直接证明经典试题的科学性——释放弹簧自由端，若台秤示数等于重物质量，也就说明释放弹簧自由端后，重物的加速度a=g。然而，在实验过程中，发现示数有一个增长变化的过程，这个时间很短，但长于视觉反应时间。那么是什么因素导致示数有一个增长过程而不是立即等于重物质量？因此，为了排除因弹簧恢复原状过程导致示数逐渐增长，特设了对照组。对照组的实验结果表明：台秤示数增长应该是台秤自身“反应”的结果，否定了弹簧恢复原状过程对重物动力学的影响。另外，弹簧摇晃摆动过程中，重物对台秤的压力确实有影响，但是这个影响很小，可以忽略不计，这进一步说明轻弹簧模型的实际意义。

上面几个实验结果综合说明：第一，弹性势能并没有凭空消失，也没有传递给重物，而是立即耗散了；第二，从宏观上的“瞬间”来看，轻弹簧模型的特点——两端作用力总是大小相等——适用于一端自由一端束缚的情况。

五、理论论证及其意义

就题目中细绳烧断瞬间，弹簧要恢复原状。从宏观实验来看，其恢复原状时间可认为是瞬间的；若从更高精度而言，弹簧恢复原状这个过程总是需要时间的，如5毫秒。那么在轻弹簧恢复原状过程中，自由端和束缚端的力总是相等吗？或者说，轻弹簧恢复原状过程中，弹簧对重物的作用力是突变的吗？回答这个问题之前，还是先来分析“这是真的吗？”(https://v.qq.com/x/page/x0766z4295a.html?)网络视频实验。

细绳直接悬挂弹簧(弹簧下端没有固定物块)，剪断细绳后，观察下端是否会有短暂的“悬浮”现象？实验结果是，不管使用质量大的硬弹簧，还是质量轻的软弹簧，剪断细绳后，弹簧都迅速恢复原状并立即自由下落，肉眼基本无法观察到弹簧恢复原状的过程。然而，在高倍率摄像机的慢镜头下，两者就有了显著差别：对质量重的硬弹簧，弹簧恢复原状过程中，下端依然难以观察到短暂“悬浮”现象；对于质量轻的软弹簧，下端观察到短暂的“悬浮”现象。

在这个实验中，不管是质量重的弹簧，还是质量轻的弹簧，都不能视为“轻弹簧”模型，因为悬挂后弹簧伸长本身就是弹簧自身重力的作用。尽管如此，运用质心运动定理分析这一实验现象是有启发意义的。细绳剪断瞬间，运用质心运动定理，弹簧质心加速度ac=g；再运用微元法分析，可以推断弹簧各处加速度具有如图4所示特征。

图4

根据图4加速度特点，对于硬弹簧，悬挂后在自身重力的作用下形变量较小，剪断细绳后，上端加速度很大，于是恢复原状时间更短，以至于在高倍摄像机的慢镜头下都难以观察这一过程，“只能”观察到整个弹簧自由下落；而对于软弹簧，形变量很大，剪断细绳后，弹簧恢复原状的过程足以在高倍摄像机的慢镜头下观察到，又由于下端加速度较小，在短时间内运动位移较小，由于肉眼对快速运动部位更为敏感，于是“观察”到软弹簧下端“悬浮”的现象。

若在软弹簧下端悬挂重物，形变量更大，上端自由释放后，下端重物位置就是质心位置，虽然其加速度ac=g(细绳剪断瞬间，加速度特征如图5所示)，但在弹簧恢复原状时间内，重物下落位移很小，而上端下落位移很大，于是在高倍摄像机的慢镜头下，依然能够“观察”到重物“悬浮”假象。教师之所以认为重物“悬浮”是假象，是基于质心运动定理的正确性做出的判断。于是建议设计更为严谨的实验加以验证，如在重物下端固定一个挡光板，运用高分辨率的光电门等设备进行监测，以弥补肉眼视觉效应之不足。

图5

六、深度反思——理想模型的建立问题

细绳剪断瞬间重物加速度到底是0还是g？其答案运用质心运动定理分析似乎已有定论，但在实验验证方面还有待进一步改进方案。尽管如此，回归理想模型之建模意义上来，或许问题就简单许多。

物理模型最核心的思维方法是，忽略次要因素突出主要因素的简化方法。对原物的认识和研究是十分复杂的，具有众多的因素，哪些因素是主要因素，哪些因素又是次要因素呢？这取决于所要研究的问题。研究问题不同，这些因素的地位也就不同，在一个问题中原本为主要因素，在另一个问题中可能变为次要因素，反之亦然。可见，物理模型不是原物的全部，是为了某个特定问题的顺利研究而纯化了的理想模型[3]。

就题目而言，重物的动力学特点是所要研究的问题，就此问题，弹簧本身的质量并不是主要因素，而是次要因素，于是质量可以忽略不计；对于弹簧弹性势能变化问题，弹簧自身因素是主要因素，如弹簧的劲度系数、弹簧内部之间的相互作用都不可忽略。在同一系统同一过程中，由于所关注的问题不同，各种因素的地位会有所变化。《条件》就把重物的动力学问题和弹簧的弹性势能问题合二为一，不加区分，从而导致思维障碍，并陷入循环论证的思维陷阱中。

另外，就同一问题，由于对所研究问题的程度要求不同，各种因素的地位也可能发生变化，从而需要建立不同的物理模型，如研究实际气体，对压强、温度和体积等状态参量的精度要求不同，建立的物理模型也就不同，若精度要求不高，选用理想气体模型则可；若精度要求较高，则要选用范德瓦尔气体模型。

就题目而言，弹簧一端自由后，弹簧恢复原状时间极短，在“分辨率”无须太高的情况下视为“瞬间”完成无可厚非，从而运用轻弹簧模型来分析得出的结论显然符合实际情况(精度无须太高的实际或精度无法太高的实际要求)。

物理模型是现象与理论的中介，以解决问题为目的，以发展物理概念、演绎推理形成物理理论为归宿。可见，物理模型是物理学家开展科学研究的普遍性思维方法，是科学知识发展的重要驱动力。物理模型的价值对于物理学家而言是十分明确的，但物理学家的模型与学生理解的模型有所不同，但在本质上没有区别。也正因为如此，通过模型的建构教学可以帮助学生聚焦问题、建构知识，在学科的范畴下进行问题解决[4]。

七、结论与拓展

与题目相仿的还有如图6情景，剪断细绳瞬间，下端重物加速度等于0，这是毫无争议的。在图6情景中，上端有重物，弹簧上端加速度不会太大，弹簧不能瞬间恢复原状；在图1情景中，上端没有重物，弹簧上端加速度很大，弹簧瞬间恢复原状，下端重物加速度等于g。这两种情景，因为弹簧质量较小均可以忽略，都可视为“轻弹簧”。网络上有一个大型实验(https://v.qq.com/x/page/u08870qe2xj.html?)很好地验证了图1、图6两情景中下端物体运动状态之不同，前者快，后者慢。