融入相关史料,凸显文化特色
2021-01-21郭茜
郭茜






摘要:勾股定理有着丰富的文化内涵和巨大的文化价值。勾股定理的教学要凸显数学文化特色,可尽量选取相关历史材料,融入定理猜想、证明与应用的全过程,在润泽学生数学情感、促进学生数学理解的同时,让学生充分体会数学文化中的探索精神、思想方法以及数学之用、数学之美。
关键词:勾股定理;教学设计;数学史;数学文化
作为初中数学的重要内容,勾股定理是平面几何最基本的定理,是数形结合的典范,有着丰富的文化内涵和巨大的文化价值。张奠宙先生说过:“勾股定理是难得的承载着大量的数学文化的中学数学课题。”因此,勾股定理的教学要凸显数学文化特色,可尽量选取相关历史材料,融入定理猜想、证明与应用的全过程,在润泽学生数学情感、促进学生数学理解的同时,让学生充分体会数学文化中的探索精神、思想方法以及数学之用、数学之美。笔者在教学中便做了这样的尝试,取得了较好的效果。
一、教学设计
(一)课前准备
推送视频微课“勾股定理的发展历史”,让学生了解与勾股定理相关的重要历史事件。
让学生上网搜索与勾股定理相关的小故事,分享给同学,并提交给教师。
[设计意图:历史材料的融入,会使得这节课的容量比较大。让学生在课前观看相关历史事件的视频,可以使他们在课堂上比较快地接收信息,从而快速进入思考、理解的状态。让学生在课前搜集相关历史材料,可以使课堂上呈现的历史材料部分甚至全部来自学生,从而更好地激发学生的学习动力。]
(二)课堂教学
1.勾股定理的猜想。
(1)探索等腰直角三角形的三边关系。
首先,分享学生课前搜集的古希腊数学家毕达哥拉斯的小故事:
相传,在公元前550年左右,有一次,毕达哥拉斯应邀去朋友家做客。善于观察的他被脚下排列规则的地砖图案所吸引,看着看着,竟然在地磚图案上做起了数学,完全忘记了自己是来做客的。地砖图案是一个个相同的直角三角形按黑白两色有规则地排列形成的。他发现,地砖图案中正方形A和正方形B的面积之和恰好等于正方形C的面积(如图1)。回家后,他又做了进一步的推广、演算,最终得到了勾股定理——西方称为毕达哥拉斯定理。
接着,出示三个问题:
问题1:地砖图案中,正方形A、正方形B和正方形C的面积为什么有上述关系?如何计算或表示三个正方形的面积?
问题2:这三个正方形中间所围的图形是什么?
问题3:如何描述结论?
(2)探索网格中直角三角形的三边关系。
首先,出示情境:
1955年,希腊发行了一枚邮票(如图2),纪念毕达哥拉斯发现勾股定理;显然,邮票中的图形可以放入网格中(如图3)。
接着,出示一个问题:
问题4:图中,三个正方形的面积是否还具有刚才的关系?如何求正方形C的面积?
预设:(1)“补”的方法,即C的面积=大正方形的面积-4个小直角三角形的面积;(2)“割”的方法,即C的面积=4个小直角三角形的面积+小正方形的面积。
然后,出示三个问题:
问题5:这三个正方形中间所围的图形是什么?
问题6:如何描述结论?
问题7:网格中,其他的直角三角形满足这个关系吗?请在课前分发的方格纸上绘制直角三角形,构造相应的正方形并求出其面积。
汇总学生的计算结果,验证结论。
(3)探索任意直角三角形的三边关系。
出示一个问题:
问题8:去掉网格限制,任意直角三角形都满足这个关系吗?
利用“几何画板”软件绘制直角三角形,构造相应的正方形并自动求出其面积;改变直角三角形的形状、大小,自动呈现变化的数据,验证结论。
根据正方形面积公式,获得猜想:如果直角三角形的两条直角边长分别为a、b,斜边长为c,那么a2 + b2=c2。
[设计意图:从毕达哥拉斯发现勾股定理最初的情境入手,从简单到复杂、从特殊到一般,一步一步做细做实,引导学生充分经历归纳猜想勾股定理的过程,不断体会一般化(推广)的数学思想。其中,引入动手操作和软件演示可以充分发挥学生的主体作用,提升学生的学习体验。此外,求网格中直角三角形斜边上的正方形的面积时采用的割、补方法可让学生体会到转化的数学思想,并且为后面理解勾股定理的证明方法(启发勾股定理的证明思路)做好铺垫。]
2.勾股定理的证明。
(1)商高的“积矩图”证法。
分享学生课前搜集的中国古代数学著作《周髀算经》中周武王的大臣周公和学者商高的一段对话:
昔者周公问于商高曰:“窃闻乎大夫善数也,请问古者包牺立周天历度,夫天不可阶而升,地不可得尺寸而度,请问数安从出?”商高曰:“数之法,出于圆方,圆出于方,方出于矩,矩出于九九八十一。故折矩,以为勾广三,股修四,径隅五。既方之外,半其一矩,环而共盘,得成三四五,两矩共长二十有五,是谓积矩。故禹之所以治天下者,此数之所生也。”
解释这段话的意思:
从前,周公问商高:“我早就听说大夫您擅长数学。古时伏羲建立周天测量度数,可是天没有台阶可供攀登,地也不适合以尺寸去度量,请问这些数是从何处得来的?”商高说:“数学的方法出于圆和方(正方形)的数理特性,圆可由方的数理特性推导,方可由矩(长方形)的直角数理特性推导,矩的数理原理出于乘法法则。所以,将矩形沿对角线一折为二,得两个相等的直角三角形,那么,勾方加股方就等于径方。例如,如果勾(即短边)等于三,股(即长边)等于四,那么,所得直角三角形的径(即弦,斜边之长)就等于五(三四五这三个数按九九乘法表来计算有三三加四四等于五五的关系)。为什么呢?您看,在直角三角形之外,以径为边作正方形,然后每次取半个矩形,四次就可以环绕正方形一周,这就形成一个大的方盘了。由此推导,就可以得出成立‘三四五’的数理关系了。因为由构图得,由两个矩形分成的四个直角三角形围成的径方的面积等于大的方盘面积(七七四十九)减去两个矩形的面积(三四一十二的两倍,二十四),从而推导得径方面积等于二十五,这恰好等于勾方的面积九加股方的面积十六,得到径等于五,这就是所说的勾三股四径五。这种推导法就是所谓的‘积矩’法。大禹之所以能够(由治水而)治天下,就得力于以上的数量关系。”
谈话:这其实就是勾股定理名称的由来。由此,我们可以知道,商高不仅发现了勾股定理,还证明了勾股定理。(课件出示图4)请观察“积矩图”,解释商高的证法。
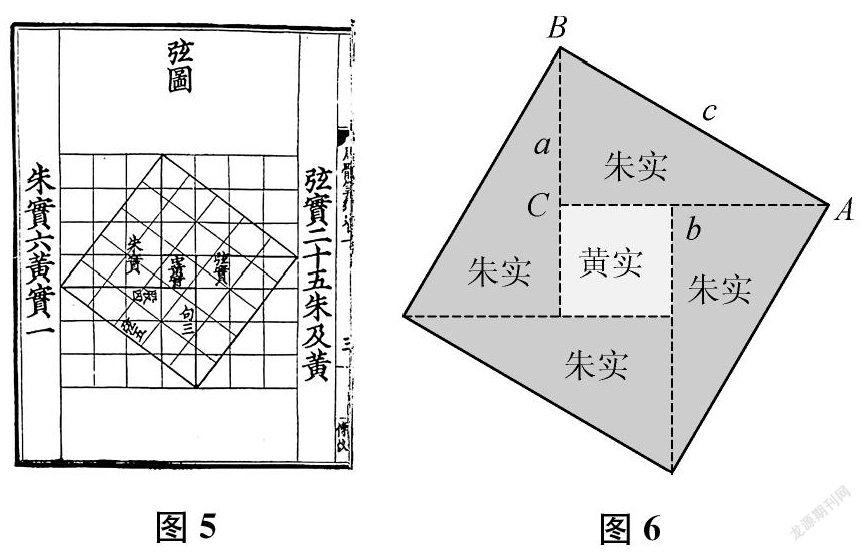
(2)赵爽的“弦图”证法。
谈话:三国时期吴国的数学家赵爽在《勾股圆方图注》一书中创制了“弦图”,(课件出示图5)再次证明了勾股定理。2002年,国际数学家大会在中国召开,会徽(课件出示会徽)就是赵爽的“弦图”。(课件将“弦图”一般化为图6)请观察“弦图”的一般化,解释赵爽的证法。
(3)刘徽的“青朱出入图”证法。
谈话:魏晋时期的数学家刘徽撰写《九章算术注》时,依据“割补术”创制了“青朱出入图” ,又一次证明了勾股定理。虽然此图失传了,但是后人根据“出入相补、以盈补虚”的原理,参照书中类似的方法,还原了此图(课件出示下页图7)。请观察“青朱出入图”,解释刘徽的证法。
(4)欧几里得的证法。
谈话:古希腊数学家欧几里得在《几何原本》中,也给出了勾股定理的证法(课件出示下页图8)。
具体解释欧几里得的证法。
(5)其他证法。
分享师生搜集的勾股定理的其他证法。
[设计意图:商高的证法、赵爽的证法和刘徽的证法简洁明了,凸显了几何直观,正是之前割、补计算面积方法的迁移运用,可以让学生尝试作出解释。欧几里得的证法逻辑严谨,在几何直观的基础上凸显了演绎推理,需要运用全等三角形知识和等积转化思想,应该向学生作出解释。通过对比,学生不仅可以感受到证法中蕴含的数学思想,而且能够体会到中西数学文化的差异。勾股定理是证明方法最多的数学定理之一。分享其他证明方法,可以拓宽学生的视野,让学生充分体会到数学知识之間的丰富联系,以及数学学习的无穷乐趣。]
3.勾股定理的应用。
出示习题:
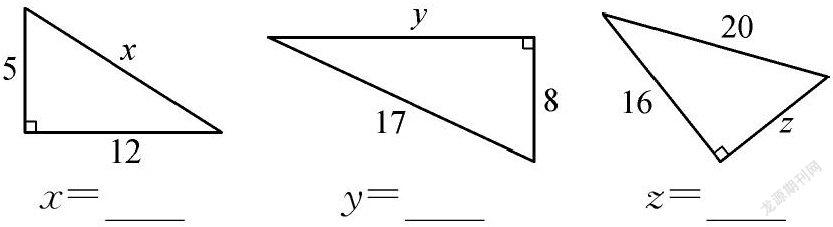
1.在下列横线上填上正确的数值。
2.已知在Rt△ABC中,a、b、c分别为∠A、∠B、∠C所对的边。
(1)若∠A=90°,a=0.5,b=0.3,则c=_______________;
(2)若∠B=90°,a=5,c=12,则b=_________________;
(3)若∠C=90°,c=15,b=9,则a=____________________;
(4)若∠C=90°,a∶b=3∶4,c=10,则a=____________,b=____________。
3.《九章算术》中有一个“引葭赴岸”问题:“今有池方一丈,葭生其中央。出水一尺,引葭赴岸,适与岸齐。问:水深、葭长各几何?”题意是:“如图9,有一个边长为10尺的正方形池塘,一棵芦苇AB生长在池塘中央,高出水面部分BC为1尺。如果把该芦苇沿与岸边垂直的方向拉向岸边,那么,芦苇的顶部B恰好碰到岸边的B′。问:水深和芦苇长各多少?”
4.(1)求图10中阴影部分的面积:SE=___________,SA+SB+SC+SD=____________。你发现了什么?
(2)请拿出之前在方格纸中绘制的图形,在原有两层图形的基础上绘出第三层。你还能绘出更多层吗?
展示“几何画板”软件绘制的“勾股树”(如图11),让学生欣赏。
[设计意图:第1题是勾股定理的基本应用,即已知直角三角形的任意两边,求第三边。第2题稍微提升难度,即不给图形,先要确定已知边是直角边还是斜边,以及变已知一边长度为已知两边长度的比。第3题是《九章算术》中的问题,是实际应用问题,既渗透了数学文化,也体现了数学之用;同时进一步提升难度,即要运用建模思想和方程方法。第4题“勾股树”问题,是规律探究和数学实验问题,既渗透了数学文化,也体现了数学之美。]
二、教学立意
(一)重走历史之路,感悟数学思想方法
弗赖登塔尔认为,数学学习应该是一个再发现、再创造的活动过程。再发现、再创造,可以使数学学习不过分着眼于琐碎的、容易遗忘的数学知识(问题),更关注获得知识(解决问题)过程中具有一般性的、能够积淀和迁移的数学思想方法和活动经验。数学教学中融入数学史,可以让学生更好地经历数学知识的发生、发展过程,完成再发现、再创造,因为历史体现(包含)着最真实的发现、创造过程。本节课,不仅定理的猜想、证明和应用环节都融入了大量的历史材料,而且,“猜想—证明—应用”这一流程也充分体现了历史发展的脉络,是对历史过程的重构。有了过程的充分经历,学生就能更好地体会到从一般化、割补转化、等积变换、几何直观、演绎推理等重要的数学思想方法以及“大胆猜想(类比、归纳),小心求证(验证、论证),广泛应用(数学、现实)”的数学研究经验。
(二)比较中西文化,体会数学之用和数学之美
勾股定理的文化内涵还充分体现了数学文化的多样性特征。本节课,在证明环节,笔者有意引导学生比较源自中国数学文化的商高证法、赵爽证法、刘徽证法和源自西方数学文化的欧几里得证法;在运用环节,笔者有意引导学生比较源自中国数学文化的“引葭赴岸”问题和源自西方数学文化的“勾股树”问题。由此,可以让学生体会到中国数学文化的实用特征和西方数学文化的理性特征,进而体会到数学同时具有的应用价值和审美价值,建立多元的数学观和文化观。
参考文献:
[1] 徐小建.弘扬数学文化,实现学科育人——李庾南老师《勾股定理》教学赏析[J].教育研究与评论(中学教育教学),2021(9).
[2] 俞求是.《周髀算经》“周公商高问答”相关问题的研究[J].数学通报,2019(2).
[3] 王海青.基于数学史和《原本》思想的勾股定理教学价值思考[J].教学与管理,2016(10).
[4] 弗赖登塔尔.作为教育任务的数学[M].陈昌平,唐瑞芬,等编译.上海:上海教育出版社,1995.
