基于HTCPN的牵引车动态优化调度

苏志刚，赵松泽，郝敬堂

(中国民航大学 中欧航空工程师学院，天津 300300)

0 引 言

快速增长的航空运输量极大增加了机场场面的运行压力[1]。目前我国大部分机场的工作人员是通过目视、语音对讲等方式对符合条件的车辆进行调度[2]，落后的信息获取方式及决策过程导致航班高峰时段调度效率低下，进而影响航班的准点率。地勤保障车辆调度问题持续受到国内外学者的广泛关注，研究方法主要集中在运筹学方法[3-7]和系统仿真方法[8-12]两个方面。

运筹学方法是将车辆调度问题简化为多目标优化模型，再利用启发式算法进行求解。启发式算法主要是对静态调度问题进行优化。即假设在航班计划、航班需求时间窗以及作业时间等信息已知并始终不变的前提下，根据航班的需求规划车辆的行驶路径。实际情况下影响航班运行的随机因素较多。当随机因素对原有航班计划产生影响时，车辆资源需要重新分配。虽然启发式算法可以得到可行解，但其不能很好地对调度过程中的随机因素实时响应。

系统仿真方法利用离散仿真模型模拟调度流程，十分适用于机场车辆调度这种存在诸多不确定因素的离散动态随机过程的分析。采用仿真方法可以很好地模拟调度过程中的突发事件，设计出针对不同随机问题的解决方案。芝加哥机场和日本民航局采用TAAM[11](total airspace & airport modeler)对空域和飞行区进行仿真研究，分析机场的运行方式和空域构型。丹佛机场利用SIMMOD[12]分析现有飞行区的运行状况以及新的改造措施对延误的影响。上述仿真软件虽然功能强大，但价格昂贵，且仿真的主要对象是航空器，仅有少部分功能涉及到车辆调度过程。

本文运用层次赋时着色Petri网(hierarchical timed colored Petri net，HTCPN)对牵引车调度过程进行仿真。利用层次Petri网(hierarchical Petri net，HPN)对系统进行模块划分，增加模型的可视性；利用着色Petri网(colored Petri net，CPN)对不同资源进行标记区分；利用赋时Petri网(timed Petri net，TPN)模拟牵引车资源占用和释放的实时情况。搭建动态调度仿真系统，根据航空器发送的推出申请完成航空器与牵引车的动态匹配。提出调度优化方案，实现不同车辆间工作负荷均衡度最高和车辆行驶总距离最短的优化目标，通过仿真实验验证了优化的有效性。最后完成对目标机场牵引车保障能力的评估，预测在不同航班密度下的牵引车配置数量。

1 牵引车调度数学模型

1.1 调度流程分析

针对牵引车调度特点，将调度流程简化为如下步骤：首先按照假设的规则随机生成离港航班信息，系统根据每架航空器的预计离港时刻非降序排列所有航班信息形成航空器等待队列，每架航空器在其预计离港时刻前TRequest分钟发出推出申请；系统按照设定的动态优化调度目标逐一为待服务航空器分配满足条件的牵引车前往服务；牵引车在开始推出任务前判断与邻近机位是否存在推出冲突，如存在冲突则在原地等待；待冲突解脱后牵引车将航空器推出到指定位置，并完成信息的记录与更新。

1.2 基本假设

机场场面运行过程中包含诸多随机因素，在不影响牵引车和航空器正常运行的前提下对模型做如下假设：

(1)单位时间内离港航空器数目服从参数为λ的泊松分布[13，14]；

(2)正常情况下，每架航空器在其预计离港时刻前TRequest=15min发出推出申请；

(3)牵引车推出航空器时与邻近机位发生推出冲突的概率为PConflict， 若存在推出冲突，牵引车和航空器在原地等待的时间满足均值为TConflict的指数分布；

(4)牵引车推出航空器的作业时间服从高斯分布N(μ,σ2)。 作业时间的均值μ由被服务航空器的机型决定。标准差σ的取值与航空器机型无关，与推出时地服人员和飞行员配合的熟练度有关。

1.3 优化目标

在现有运行模式下，调度部门收到推出申请后，会按照车辆序号顺序分配可用车辆。如果存在可用车辆，立刻分配该牵引车从当前位置驶向指定机位进行服务。若所有牵引车当前时刻均处于工作状态，调度人员会根据反馈信息指派最先完成当前任务的牵引车执行该任务。现行调度规则存在以下问题。

(1)每辆牵引车航班任务分配不均衡；

(2)为航空器分配牵引车时没有考虑候选车辆与服务需求点间的距离。

为解决当前调度模式下存在的问题，需要依次从车辆到达时间、车辆工作负荷均衡度和车辆行驶距离3个方面进行优化。

车辆到达时间：在实际运行中时间因素最为重要，要求车辆延误到达的时间最少

(1)

式中：ti表示第i架航空器因牵引车晚点造成的延误时间，式(2)是表示延误与否的符号函数

(2)

车辆工作负荷均衡度：为保证牵引车的安全使用和驾驶人员的合理分配，调度车辆时应尽量提高不同车辆间工作负荷的均衡度，本文采用车辆间工作负荷差的累积和作为表征均衡度的目标函数

C2=min∑i,j∈V|Ni-Nj|

(3)

式中：V表示牵引车的集合，Ni和Nj表示编号为i和j的牵引车服务过的航班数量。

车辆行驶距离：牵引车在不同机位间往返的距离不可忽略，减少行驶距离可进一步保证牵引车的准时到达，同时降低机场或航空公司的燃油成本

C3=min∑i∈VDi

(4)

式中：Di表示编号为i的牵引车行驶过的总距离。

2 HTCPN动态调度仿真系统

2.1 模型描述

建模采用自顶向下的分解原则。首先确定调度流程的整体功能模型图，然后再对顶层模型进一步细化，在子页中实现子流程功能，形成分层模型。牵引车动态调度仿真系统的层次赋时着色Petri网模型可简化为以下多元组

HTCPN=(S,SN,SA,PN,PT)

(5)

HTCPN中各参数的含义分别为：

(1)S代表子页的有限集合，每个子页对应于调度过程中一个关键的子流程，依次为航空器推出申请、航空器牵引车实时匹配、航空器推出冲突、航空器推出过程。S中的任意子页s均是一个非层次的赋时着色Petri网

s=(CPN,R,r0)

(6)

式中：R是时间值的集合，称为时间戳；r0是R中的元素，对应于调度过程的起始时刻。

(2)SN是替代变迁，SN⊆T，T表示变迁集合，采用变迁代表Petri网结构中的某一模块，使得网络在逻辑上得到简化，之后在对应的子页再进行更深层次的精细化建模。

(3)SA是页分配函数，SA∶SN→S， 表示子页和替代变迁间的对应关系。

(4)PN代表端口节点的集合，PN⊆P，P表示库所集合。

(5)PT是端口类型函数，是从PN定义到{In,Out,In/Out,General} 的函数。

式(6)中的参数CPN表示一个非层次的着色Petri网，可用如下9元组表示

CPN=(P,T,A,Σ,V,C,G,E,I)

(7)

式中：P表示库所集合，以椭圆形表示，可以表示动态调度仿真系统各资源的实时状态；T表示变迁集合，以矩形表示，代表调度中每个具体事件的发生，实现不同库所间的信息传递；A为有向弧集合，是联系库所和变迁之间的流关系；Σ为颜色集的非空有限集合；V为变量集合；C为颜色集函数，定义库所的数据类型；G为变迁上的守卫表达式，E为有向弧表达式，守卫表达式和弧表达式共同定义了变迁的使能条件；I为初始化函数，定义库所的初始标记。

托肯(token)表示分配给库所的资源，在Petri网模型的执行过程中会发生个数和位置的变化。牵引车和航空器是模型中两种不同类型的资源，分别对其着以不同的颜色进行分类。变迁触发后会从其输入库所移出托肯，同时向输出库所增加托肯, 从而引起模型状态的改变。航空器与牵引车的颜色集见表1。

表1 航空器与牵引车颜色集

航班号、停机位、牵引车编号等初始属性的作用是对托肯的活动进行约束，牵引车到达时刻、牵引车已服务航班序列、牵引车当前位置等属性则会随系统的运行实时更新，更新后的结果将成为后续运行中新的约束条件。

2.2 顶层模型

动态调度仿真系统的顶层模型如图1所示。替代变迁用双框矩形表示，各替代变迁的含义见表2。

表2 顶层模型中替代变迁及其对应子过程

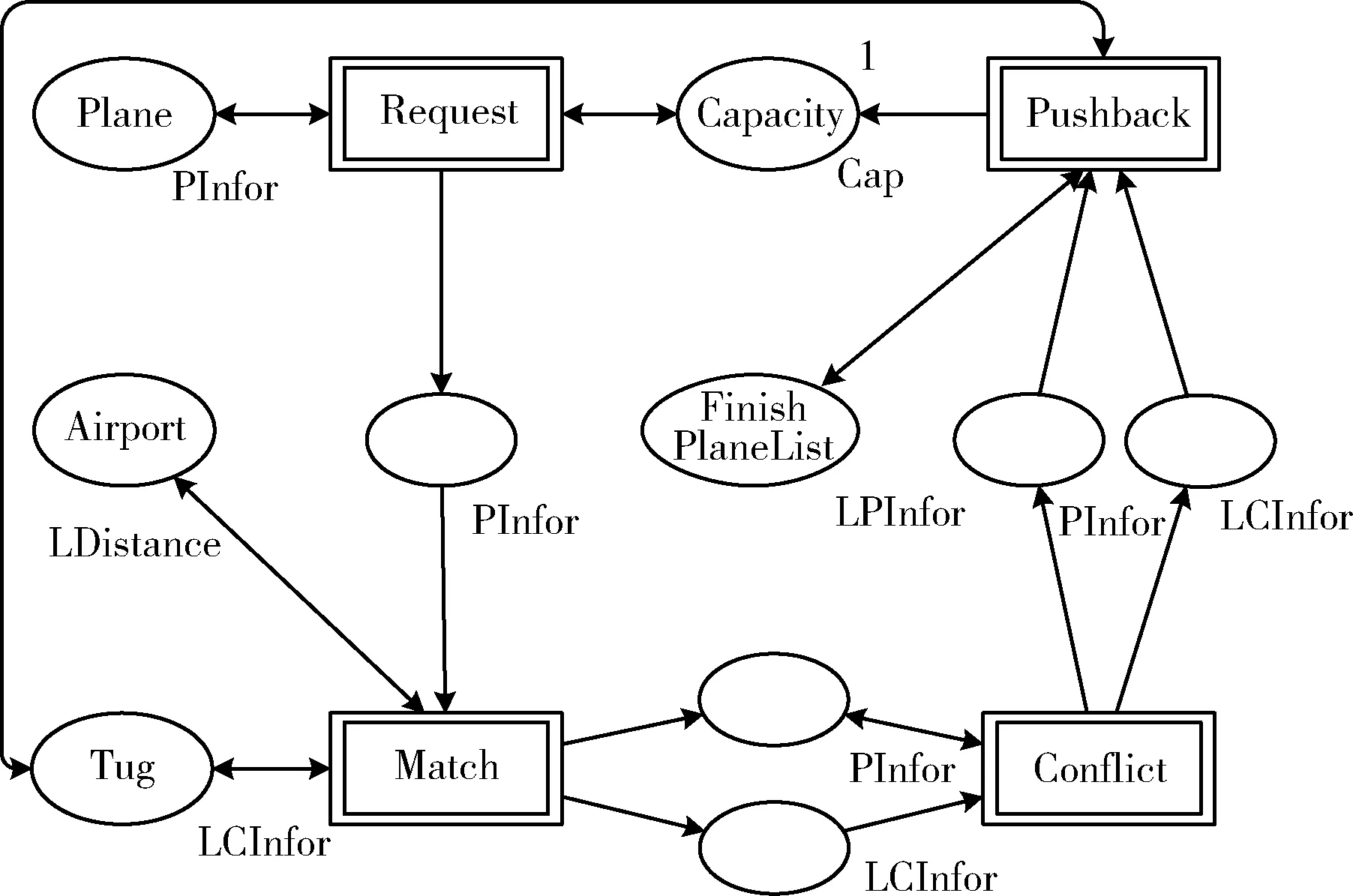
图1 牵引车调度顶层模型

库所右下方的标识代表颜色集，根据容纳的资源类型分为4类：航空器状态库所(PInfor)、航空器队列状态库所(LPInfor)、牵引车集合状态库所(LCInfor)和约束类库所(LDistance,Cap)。

库所Plane存储系统随机生成的航班信息，库所Tug存储机场内初始时刻所有牵引车的信息，库所Airport对应于机坪不同位置点距离的录入，以上3个库所是模型中初始信息的输入窗口。所有航空器会依次通过4个替代变迁，最终回到Finish PlaneList库所中，该库所的作用是记录每架航空器被推出后的最终状态。此外，库所Capacity对航空器等待队列起到容量约束的作用。在库所和替代变迁的共同作用下，调度过程的HTCPN模型形成一个闭环反馈结构。

2.3 航空器推出申请

顶层模型中表示航空器推出申请的替代变迁(Request)展开后可得到如图2所示的子页模型。

图2 航空器推出申请模型

系统首先通过Timetable变迁在一定规则下随机生成航班数据。该变迁守卫表达式中的density用于模拟服从泊松分布的航班流。库所Apron中存储系统自动生成的离港航空器所在停机位编号，分配时采取随机原则，同时确保同一机位在2小时内不会被再次分配。生成的航班信息在List中以列表的形式存储。List中的航班列表再通过Sort变迁完成按预计离港时刻的非降序排列，在Queue中形成航班的等待队列。最后通过Request变迁逐一发出推出申请。通过Capacity库所可以使系统逐一地接收航空器队列发出的推出申请，从而实现对航空器等待队列的容量约束。端点为空心圆的弧为抑制弧，作用是设置变迁发生的优先权。当库所Plane中存在托肯时，变迁Sort无法发生，通过抑制弧使排队过程在航班信息生成后进行，从而可以自主控制仿真实验中的航空器数目。Request变迁输出弧上的applytime是航空器发出推出申请的时刻，作为每架航空器初始状态下携带的时间戳。

2.4 航空器牵引车实时匹配

基于贪婪算法设计了航空器牵引车实时匹配算法。贪婪算法是以当前情况为基础追求局部最优解，可以针对航空器队列发出的推出申请逐一完成牵引车的分配，对动态调度问题有一定的解决能力，航空器牵引车实时匹配算法如图3所示。

图3 航空器牵引车实时匹配算法

系统在读取待服务航空器发出的推出申请后，依次以车辆到达时间、车辆工作负荷均衡度以及车辆行驶距离为判据筛选出满足条件的牵引车集合。

首先实现车辆到达时间的匹配，筛选出当前时刻处于空闲状态的牵引车集合，如若没有空闲车辆，则选定完成当前任务时刻最早的牵引车。车辆工作负荷均衡度匹配是对每辆牵引车服务过的航班数进行非降序排列并筛选出服务航班数最少的牵引车集合。最后再对每辆牵引车行驶总距离完成非降序排列，筛选出行驶总距离最少的牵引车，从而实现车辆行驶距离的匹配。若此时满足条件的牵引车仍多于一辆，则按照车辆序号顺序随机指派一辆牵引车前往服务。

基于上述算法建立了如图4所示的航空器牵引车实时匹配模型。

图4 航空器牵引车实时匹配模型

模型中从上至下的3个替代变迁分别对应于流程图中的车辆到达时间匹配、车辆工作负荷均衡度匹配和车辆行驶距离匹配。每个替代变迁后的节点库所分别表示航空器的最新状态和经过筛选后的牵引车集合状态。

发出推出申请后的航空器首先与牵引车集合Tug同时绑定于Arrival Time替代变迁，目的是筛选出满足时间要求的牵引车集合。经过第一步筛选后的牵引车集合和航空器同时绑定于Load Balance替代变迁，筛选出服务航班数辆最少的牵引车集合。Airport以邻接矩阵的格式存储目标机场内不同位置点间的距离，通过Distance替代变迁搜索出每辆牵引车当前位置与待服务航空器间距离并计算出行驶到目的点的时间。经过3个替代变迁筛选后产生唯一满足条件的牵引车，系统安排该牵引车前往相应的停机位进行服务。

2.5 航空器推出冲突

在机场运行高峰时段，邻近停机位航班常会因离港时间过近而引发冲突。当航空器侧向推出时与同侧邻近停机位上另一正要推出的航空器由于安全间隔而产生冲突[15]，发生推出冲突后的解决方案是后机在原地等待，只有当前机推出并滑行通过推出安全点后，后机才能开始推出，推出冲突会导致牵引车使用时间的增加以及实际推出时间的延迟，推出冲突的模型如图5所示。

图5 航空器推出冲突模型

待服务航空器与上一步筛选出的牵引车同时绑定于变迁Ran，通过Ran在库所Conflict中产生随机数ran，再根据Normal和Wait上的守卫函数判断航空器推出冲突事件是否发生。当ran>P时，变迁Normal使能，航空器正常推出；当ran≤P时，冲突产生，变迁Wait使能。P表示发生推出冲突的概率。时间延迟delay表示产生推出冲突后航空器和牵引车需要在原地等待的时间。

2.6 航空器推出过程

航空器推出后伴随着牵引车和航空器信息的更新，航空器推出过程模型如图6所示。

图6 航空器推出过程模型

首先通过替代变迁UpdateTug，代表牵引车的托肯重新回到牵引车资源库所(Tug)，此时牵引车服务过航班序列、当前时刻位置、可为下一航班开始服务时刻、行驶总距离等属性随之更新。下一步再通过替代变迁UpdatePlane完成航空器信息的更新，代表航空器的托肯进入已被推出航空器队列库所(Finish PlaneList)，记录航空器被服务后的最终状态，包括匹配的牵引车编号、牵引车到达时刻、开始推出时刻、完成推出时刻等属性。推出任务完成后容量库所中的托肯也完成更新，服务对象转变为下一架发出推出申请的航空器。

3 系统仿真分析

选定天津滨海国际机场作为研究对象，验证HTCPN动态调度仿真系统解决实际问题的有效性。机场停机位布局如图7所示，特种车辆需严格按指定路线行驶，即图中各停机位之间的连接线，牵引车的停车场位于118号和201号停机位之间。

图7 天津机场停机位布局

根据地理位置可以得出不同地面点间的邻接关系，并计算出任意两个地面点之间的最短距离。根据文献[16]中的通用配置方法可估算出天津机场牵引车理论配置数量为12辆。表3为仿真实验中假设的推出作业时间均值与机型的关系。

表3 作业时间均值

基于蒙特卡洛方法[17]对高峰时段的牵引车动态调度进行仿真分析，仿真系统中初始设定航班密度λ=25架次/小时，牵引车行驶速度v=20km/h，作业时间的标准差σ=0.5min，推出冲突发生概率PConflict=20%， 原地等待时间均值TConflict=5min。 在不同的服务航班数量下分别进行100次独立实验，图8和图9显示了牵引车工作负荷均衡度和牵引车平均行驶总距离优化前后结果的对比。

图8 车辆间工作负荷差累积和

图9 牵引车平均行驶总距离

图8的纵轴是表征不同车辆工作负荷均衡度的负荷差累积和∑i,j∈V|Ni-Nj|， 优化前车辆负荷差累计和与服务航班数量呈现正相关的趋势。优化后的结果大幅降低，负荷差累计和随航班数量的增加近似周期性变化，在服务航班数量为60时达到最低点，由于实验中12辆牵引车被分配的任务数几乎相等，所以车辆间工作负荷差累积和趋近于0。

由图9可见，场面内所有牵引车平均行驶总距离与服务航班数量的关系。随着服务航班数量的累加，行驶总距离的优化结果会更为显著。

为体现仿真系统对随机变化的动态反应，在保证离港航班信息相同的前提下，可以将系统中一些随机化处理的数据转化为固定的常量再次实验后进行对比分析。在对照组实验中，将发生航空器推出冲突的概率设置为0，牵引车推出航空器的作业时间不再服从高斯分布，所有航空器的推出时间均为5 min。

表4中分别罗列了引入常量数据和随机数据每辆牵引车依次服务过的航班序列。

表4 牵引车服务过航班序列

结合每个航空器托肯最终状态下携带的牵引车到达时刻、开始推出时刻和完成推出时刻分别绘制了两次实验结果对应的甘特图，如图10和图11所示。

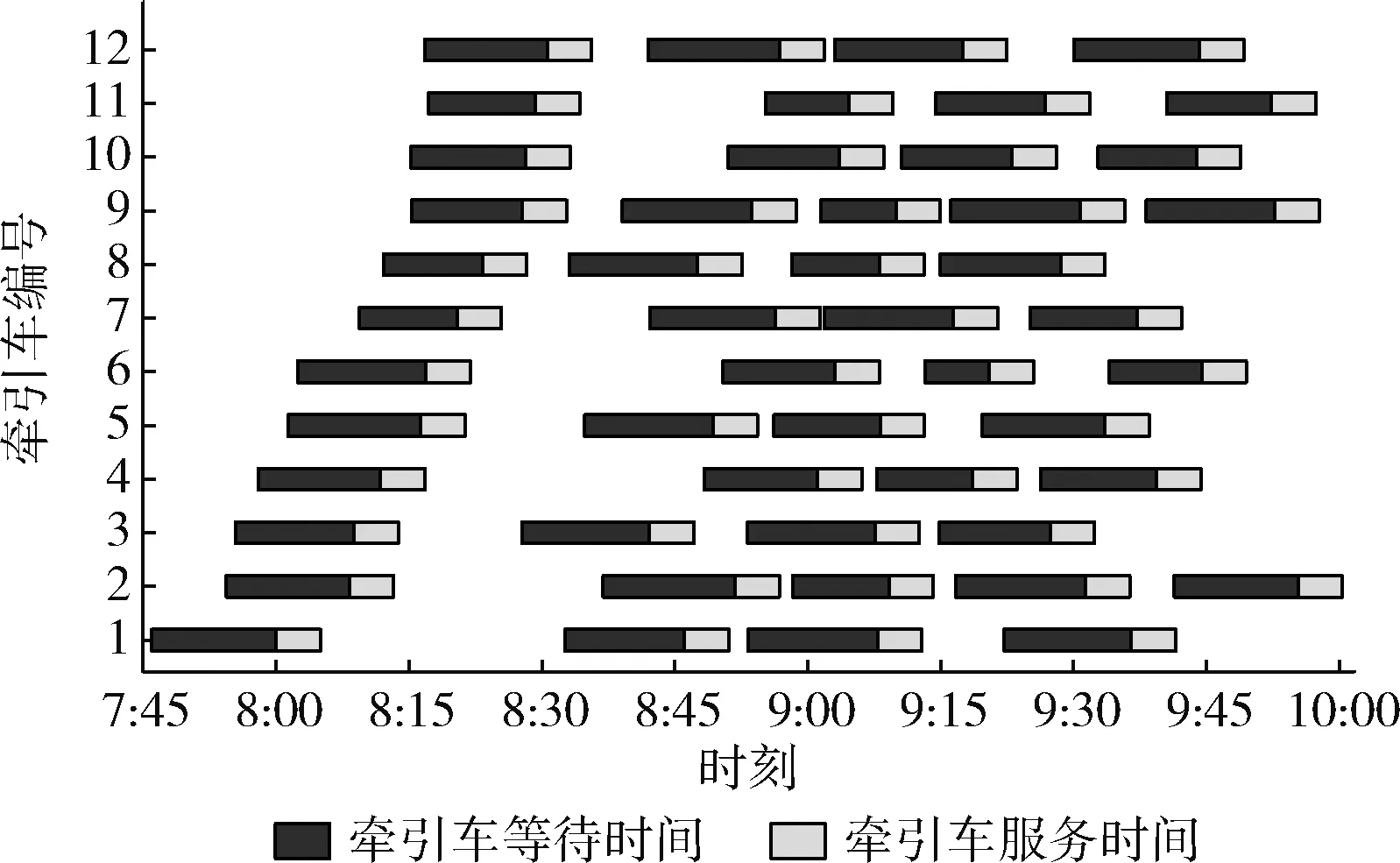
图10 采用常量数据时牵引车调度结果

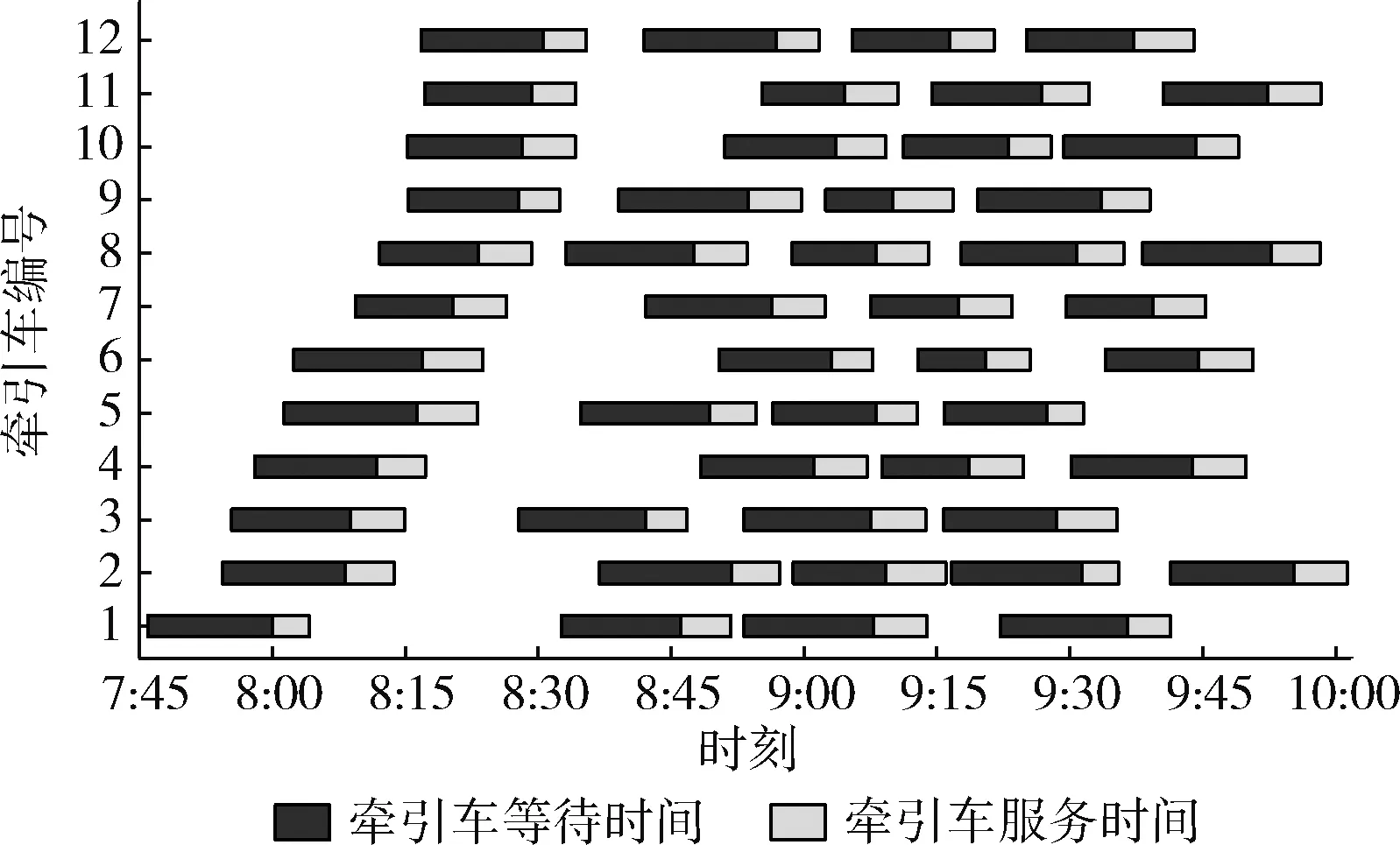
图11 采用随机数据时牵引车调度结果

综合表4、图10和图11可以发现，当考虑到航空器发生推出冲突的可能性以及推出时间分布的随机性后，牵引车的等待时间和服务时间会相应地受到影响，此时系统会以当前情况为基础追求局部最优解，因此航空器与牵引车的匹配方案较采用常量数据时产生了较大的变化。

民航局相关文件规定，牵引车应在待服务航空器预计离港时刻前5 min到位，否则将被视作晚点到达。由图10和图11可见，每个航班任务的牵引车等待时间均大于5 min，表明没有延误发生，且优化后每辆牵引车的任务量得到了合理的分配。

调整航班密度λ和牵引车数量N进一步评估天津机场牵引车的保障能力。在每组参数下进行200次蒙特卡洛实验，牵引车晚点率随λ和N的变化关系如图12所示。

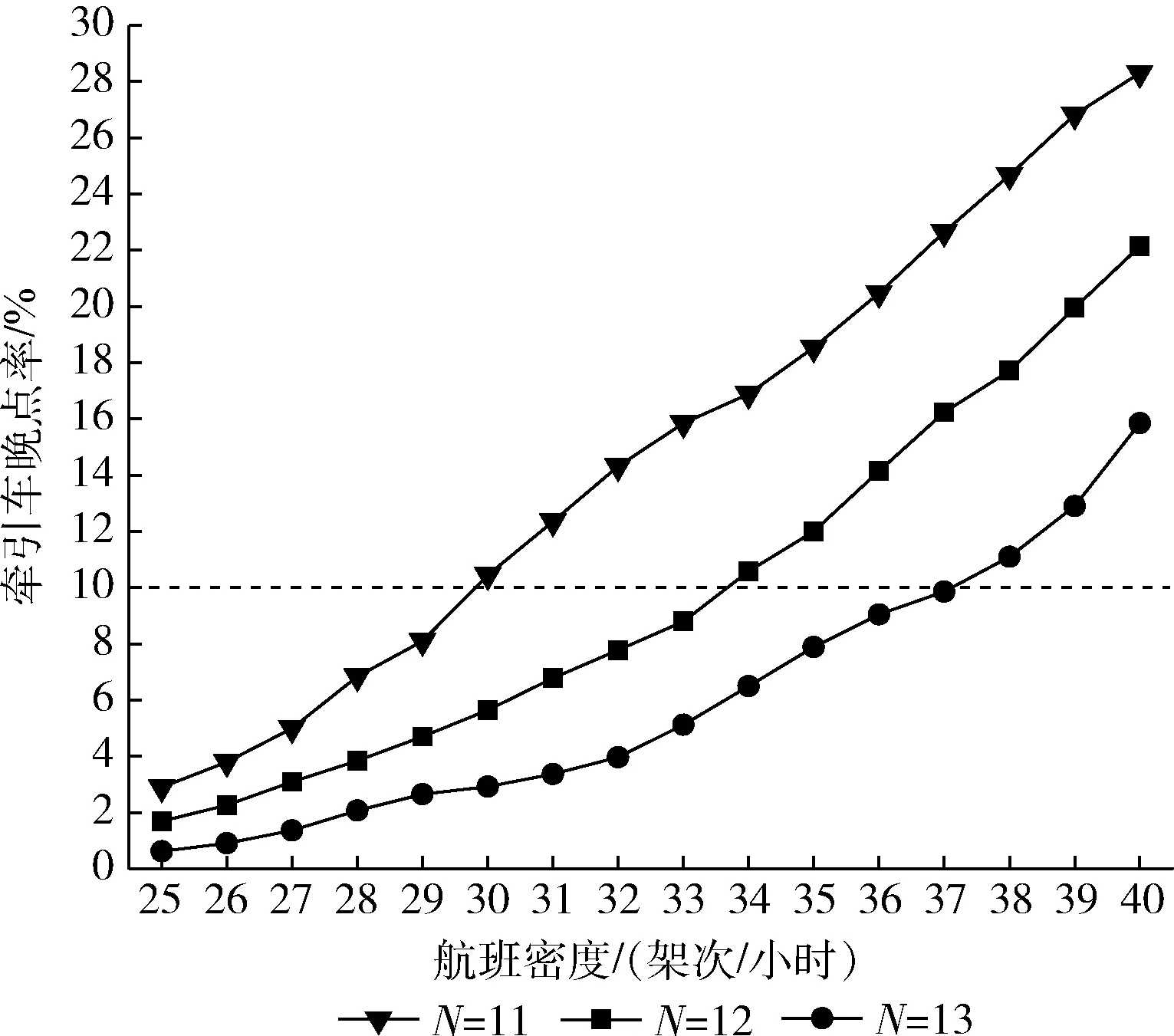
图12 牵引车晚点率变化曲线

选择以晚点率10%作为评估保障能力合格与否的临界值。从图中可以发现，当λ≤29架次/小时，11辆牵引车就可以将晚点率控制在10%之下，表明机场当前配置的12辆牵引车是冗余的，此时可适当减少场面内牵引车的使用数量；当30架次/小时≤λ≤33架次/小时，当前机场配置刚好满足准点要求，牵引车数量应当维持现状；当34架次/小时≤λ≤37架次/小时，现有配置已无法满足需要，配置13辆牵引车才可使得晚点率降低到10%以下；当λ继续增大时，在现有配置下增加两辆牵引车才可有效改善牵引车的延误问题。

4 结束语

基于层次赋时着色Petri网理论搭建了机场牵引车动态调度仿真系统。根据航空器实时发送的推出申请完成牵引车的动态分配。同时考虑了运行过程中各个环节的随机性以及高峰时段可能发生的推出冲突问题。在还原机场现有调度模式的基础上，对调度过程进行了多目标优化，首先实现航班延误最少这一基础目标，之后依次实现不同车辆间工作负荷均衡度最高和车辆行驶总距离最短的优化目标。以天津滨海国际机场为例，通过蒙特卡洛实验验证了优化的有效性，同时验证了本方法可以对目标机场的牵引车保障能力进行评估，最后通过本方法预测出在不同航班密度下必要的牵引车配置数量。