利用Petri网特征结构的故障诊断方法
2014-10-11叶丹丹罗继亮
叶丹丹,罗继亮
(华侨大学 信息科学与工程学院,福建 厦门361021)
1 基本概念和定义
Petri网结构表示为N=(P,T,Pre Post).其中:P是库所的集合,P={p1,p2,…,pn};T是变迁的集合,T={t1,t2,…,tm};Pre:P×T→{0,1,…}是前向关联矩阵,定义了从库所到变迁的有向弧的权值;Post:T×P→{0,1,…}是后向关联矩阵,定义了从变迁到库所的有向弧的权值.标识是n维的列向量m,其元素m(j)是第j个库所的托肯数目.m0是系统的初始标识,变迁tj可表示为一个m维向量δj,其第j分量等于1.当tj发生后,系统到达新标识m′=m+D·δj.其中:D=Post-Pre称为关联矩阵;变迁序列表示为δ,也可以描述为一个激发向量δ,其各分量等于相应变迁在δ中出现的次数.
在一个Petri网结构里,存在一个向量y∶P→Z.如果y≥0,并且y·D=0,可以得到

整个系统若是可以正常运行,则标识m要满足方程(1).
定义1 设R为集合S上的一个关系,则集合{x∈S|(x,y)∈R,至少一个y∈S}称为R的支集,记做SuppR,则Suppy={p∈P|y(p)≠0}.
定义2 Petri网结构里的一个库所不变量y,若不存在另一个库所不变量y′≠y,使得Suppy′⊂Suppy,则该库所不变量y为最小库所不变量.
定义3 如果最小库所不变量y中各元素的最大公约数为1,那么y称为严格最小库所不变量.y1就是严格最小库所不变量,而y2,y3不是严格最小库所不变量.
自Porod和Kratky提出蠕虫状链模型以来,运用此模型处理诸如DNA等较为刚性长链的研究逐年增多.近年来,随着DNA研究的迅猛发展,蠕虫状链模型也重新被广泛应用.例如,有关蠕虫状链模型应用的文献自2006—2016年的十年间累计达1 552篇(数据来自SciFinder数据库).因此,厘清一些基本概念就显得非常重要.
定义4 在一个Petri网结构里,如果Y是严格最小库所不变量组成的集合,并且其中元素是库所不变量的最大线性无关组,那么Y称为特征库所不变量集.
特征库所不变量集Y蕴含Petri网结构的系统信息,即Petri网中所有库所不变量可由该集合中元素线性表示,它表征了由严格最小库所不变量为基底向量所构成的空间.若系统可以正常运行,则系统Petri网结构中所有库所间的关系须包含于该空间内.
定义5 在一个Petri网结构里,Y是一个特征库所不变量集.设Y内包含k个元素,那么标识m的故障矩阵定义为k×n维的矩阵T(m),它需要满足下列条件
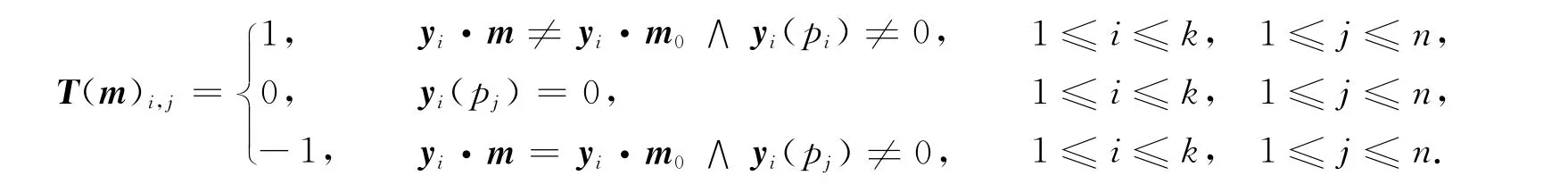
从严格最小库所不变量yi中,可以获取非零列(j列)所对应的库所pj所携带的系统信息.若在任意当前标识m下,库所间关系不满足严格最小库所不变量yi,则在该yi中携带系统信息的库所pj可能存在故障,记其T(m)i,j为1;同理,若库所间关系满足严格最小库所不变量yi,则该yi中携带系统信息的库所pj无故障,记其T(m)i,j为-1;而yi中零列,即不体现系统信息的库所pj的故障情况未知,记其T(m)i,j为0.
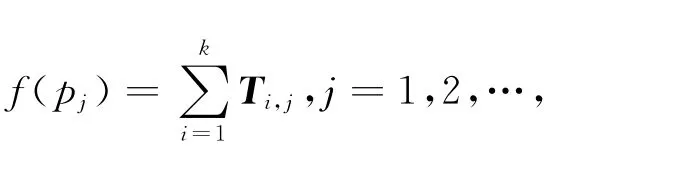
故障函数表征了系统的故障信息,即各个库所发生故障概率的相对大小,某一个pj库所的故障函数f越大,则其发生故障的可能性越高.在诊断故障的过程中,计算出每个库所的故障函数,取其中最大值,也就是故障最有可能发生的库所,这样就可以锁定故障范围了.
2 故障诊断算法及其分析
输入:Petri网N,m0和任意当前标识m;输出:故障概率最大的结点(库所).
步骤1 求出Petri网N的关联矩阵D;
步骤2 利用方程(1),计算一个特征库所不变量集Y={y1,y2,…,yk},k∈Z+;
步骤3 判断yi·m=yi·m0,i=1,2,…,k,等式是否成立;如果上述等式均成立,则没有故障发生,算法退出;否则,执行下一步;
步骤4 根据定义5,计算故障矩阵T(m);
步骤5 根据T(m)和定义6,计算故障函数λm;
步骤6 比较n个库所的故障函数λm(pj),选出最大的λm(pj),则故障出现在第j个库所的概率最大,退出算法.
在算法中,根据给定的系统Petri网的模型,首先可以求得该Petri网的关联矩阵D.如果当前标识m可以从初始标识m0到达,则其必须满足m=m0+D·δ.在式子的两边同时右乘n维的矩阵y,可以得到y·m=y·m0+y·D·δ.当y·D=0时,即y·m=y·m0,对于任何从初始标识m0开始可达的标识m都满足托肯的总数是不变量;如果Petri网模型代表的是一个正常运行的系统,则对于任何可达的当前标识m都满足约束条件y·m=y·m0,通过方程y·D=0去寻找库所不变量y.
解这个齐次方程,利用该方程的基础解系,可以表示空间中满足该约束的任意库所不变量y,用一个集合表示基础解系,即特征库所不变量集Y={y1,y2,…,yk},k∈Z+.在这个集合中,每一个元素都需要满足这个约束条件y·m=y·m0.如果每一个元素都满足该约束,即总共有k个等式成立,则证明在当前标识m0下,没有故障发生.如存在约束条件不满足情况,需要进一步去解决;如果是第i个约束方程不相等,即表示故障有可能会发生.在第i个方程中对应的库所不变量yi中,第m个为非零的列,代表第m个库所中可能存在故障,增加该库所故障发生的可能.令对应的非零列中的故障函数为+1,零列库所不变,将这个新的列向量作为故障矩阵T(m)的第i行.如果是第j个约束方程相等,即表示故障不会发生,在第j个方程中对应的库所不变量yi中,第n个为非零的列,代表第n个库所中不会存在故障,降低该库所故障发生的可能.令对应的非零列中的故障函数为-1,非零列保持不变,同样作为新的列向量作为故障矩阵T(m)的第j行,最后将T(m)中每一个库所的故障函数加大一起,选出最大值,即故障发生的可能性最大.
在算法中,当改变任意标志,就需要重新计算步骤3~6.当系统复杂性增大时,由于故障矩阵和故障函数计算的复杂度是由特征库所不变量集决定,而特征库所不变量集是根据Petri网结构的关联矩阵计算得到的,也就是说随着系统复杂性的增大,关联矩阵的维数会增多,而特征库所不变量集中的元素是库所不变量y,根据齐次方程y·D=0,会随着关联矩阵的维数增多,该齐次方程的解是呈现多项式级增长,因此算法的复杂度也是多项式级的,这在工程应用上可以得到实现.
3 实例分析
图1为某液体火箭发动机启动过程的Petri网模型[12].此图主要针对启动过程建,所以省略了对单一设备运行参数的事件监控,例如涡轮转速限幅监控事件.图1中各结点的物理意义如表1所示.表1中:p5是p0状态中的一个子集,即整个系统就绪(p0)包括了涡轮泵就绪状态.
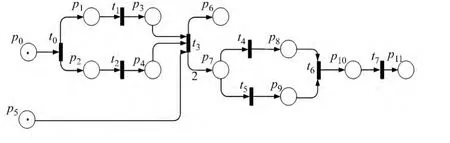
图1 液体火箭发动机启动过程Petri网Fig.1 A Petri net for the starting process of liquid propellant rocket engine

表1 图1Petri网中各结点的物理意义Tab.1 Correspondence of each transition and places Petri nets in figure 1to its physical meaning
基于上面给定的Petri网模型,根据算法可以算出该液体火箭发动机启动过程的的关联矩阵D为




因此,当前标识m′对应的故障矩阵为

下面需要验证实例的正确性.首先根据给定的Petri网模型,可以得到该Petri网系统的可达图,如图2所示.在图2中可以看到:任意当前标识下,库所p5和p6中是不可能同时存在托肯的;同样从火箭启动的过程中看到,只有当燃烧剂到达预燃室、氧化剂到达预燃室以及涡轮泵准备就绪时,托肯才有可能到达涡轮泵测速状态,与可达图相符.在给定的当前标识m′=[0 1 1 0 0 1 1 0 0 0 0 0]T下,库所p5和p6中同时存在托肯,并且库所p1和p2中也存在托肯.从图2可以看出:当p1和p2中存在托肯时,库所p5中必然存在托肯,所以最大可能是库所p6违背了可达图的演化规则,即p6中出现故障的概率最大,这也验证了算法的正确性.

图2 液体火箭发动机启动过程的Petri网可达图Fig.2 Reachable graph of the starting process of liquid propellant rocket engine in Petri nets
4 结束语
在分析文献方法中的计算效率低、故障诊断不及时、故障定位模糊等缺点后,提出了基于Petri网特征结构的故障诊断方法.给出了特征库所不变量集的定义,提出了故障矩阵和故障函数的概念,并利用数学计算来进行故障定位.该方法使得故障诊断更加快速,故障定位更加精确,由于是多项式级的计算复杂度,同样利于工程应用.
[1] SAMPATH M,SENGUPTA R,LAFORTUNE S,et al.Diagnosability of discrete-event systems[J].IEEE Transac-tions on Automation Control,1995,40(9):1555-1575.
[2] MOSTERMAN P J.Diagnosis of physical systems with hybrid models using parameterized causality[C]∥Proceedings of the 4th International Workshop on Hybrid Systems:Computation and Control.London:Springer-Verlag,2001:447-458.
[3] ASHLEY J,HOLLOWAY L E.Qualitative diagnosis of condition systems[J].Discrete Event Dynamic Systems,2004,14(4):395-412.
[4] HADJICOSTIS C N,VERGHESE G C.Monitoring discrete event systems using Petri net embeddings[J].Lecture Notes in Computer Science,1999,1639(1):188-208.
[5] CABASINO M P,GIUA A,LAFIRTYBE S,et al.Diagnosability analysis of unbounded Petri nets[C]∥Proceeding of the 48th IEEE Conference on Decision and Control.Shanghai:IEEE Press,2009:1267-1272.
[6] GIUA A,SEATZU C.Fault detection for discrete event systems using Petri nets with unobserved transitions[C]∥Proceeding of the 44th IEEE Conference on Decision and Control.Seville:IEEE Press,2005:6323-6328.
[7] GENC S,LAFORTUNE S.Distributed diagnosis of place-bordered Petri nets[J].IEEE Transactions on Automation Science and Engineering,2007,4(2):206-219.
[8] LEFEBVRE D,DELHERM C.Diagnosis of EDS with Petri net models[J].IEEE Transactions on Automation Science and Engineering,2007,4(1):114-118.
[9] YU R,HADJICOSTIS C N.Fault diagnosis in discrete event system modeled by partially observed Petri nets[J].Discrete Event Dynamic Systems,2009,19(4):551-575.
[10] CABASINO M P,GIUA A,POCCI M,et al.Discrete event diagnosis using labeled Petri nets:An application to manufacturing systems[J].Control Engineering Practice,2011,19(9):989-1001.
[11] CABASINO M P,GIUA A,SEATZU C.Diagnosis using labeled Petri nets with silent or undistinguishable fault event[J].IEEE Transactions on System,Man,and Cybernetics-Part A:Systems and Humans,2013,43(2):345-355.
[12] 郑永煌,田锋,李人厚,等.基于Petri网的液体火箭发动机启动过程实时在线故障诊断方法[J].信息与控制,2010,39(2):207-211.
[13] HASHIZUME S,YAJIMA T,KUWASHITA Y,et al.Integration of fault analysis and interlock controller synthesis for batch process[J].Chinese Journal of Chemical Engineering,2008,16(1):57-61.
