基于属性纯度的决策树归纳算法

姚岳松，张贤勇+，陈 帅，邓 切

(1.四川师范大学 数学科学学院，四川 成都 610066；2.四川师范大学 智能信息与量子信息研究所,四川 成都 610066)

0 引 言

决策树模型是基于规则的分类方法的典型代表，广泛应用于医疗、社会学、金融等领域[1-6]。决策树通常有两类构造算法。一类是基于信息熵的算法，例如经典的ID3算法[7]和C4.5算法[8]，以及C4.5的改进算法[9-11]、ID3的改进算法[12]。粗糙集理论能够进行规则提取与知识获取，其中的属性重要度是依赖性推理的核心度量[13]。由此，基于属性依赖度的特征选择提供了决策树构造的另外一类方法，即基于粗糙集的算法[14-16]。

属性依赖度来源于下近似集成的分类正域[13]，由于要求条件粒完全包含于决策类，使得基于粗糙集的决策树模型抗噪能力不强。实际数据环境下，条件粒存在不协调于决策类的情况，从而基于粗糙集的决策树模型通常需要结合信息熵函数。关于特征选择的节点度量函数，信息熵刻画不确定性结构的信息，属性依赖度与粒度推理的代数表示有关；两种机制的异质性降低了分类效果。对于分类精度而言，属性依赖度源于分类正域的定性特征，其本质是分类精度的定性和绝对度量。因此，本文首先提出了一种定量的分类准确度指标——属性纯度，而相关的特征选择对分类精度也是有效的。进而，基于属性依赖度与属性纯度的同质异态性，采用“属性依赖度优先、属性纯度补充”的二级选择策略，建立一种新的决策树归纳算法，改进基于粗糙集的决策树算法。

1 决策树基础

机器学习中，决策树根源于决策表的形式化结构。决策表是以行和列的形式描述决策规则和知识信息的表，可以推导出决策规则并可对数据进行分类。决策树采用一种树形结构表示，每一个属性上的测试(该属性也可称为分裂属性或分裂点)用内部节点表征，一个测试输出在树中表示为分支，而分支上的叶节点包含一种类别。决策树是一种决策分析的图解方法，本质上是一种监督学习形成的分类器，直观表示决策表中的决策规则与分类结果。

属性序列将决策表中的样本划分为集族，最终条件粒隶属于相关的决策类，将该过程称为决策树构造。由此可见，决策树构造与条件属性的特征选择直接相关，而相关的优化准则关联于属性重要性程度指标，不同的度量函数衍生出相应的决策树归纳算法并决定着分类效果。下面基于决策表回顾两种基本的决策树算法，其中属性度量主要涉及信息熵与属性依赖度。

1.1 决策表

决策表可表示为4元组

DT=(U,AT=C∪D,{Va|a∈AT},{Ia|a∈AT})

(1)

其中，U是一个非空的且有限的论域，AT是一个非空的且有限的属性集合(含不相交的条件属性集C与决策属性集D)，Va是属性a∈AT在决策表中所对应的值域，信息函数Ia∶U→Va呈现出关于属性a对象x的唯一数值Ia(x)。

决策表分析侧重于规则提取和依赖性推理。在这方面，主要涉及到决策分类和条件分类以及粒结构之间的交互关系，下面给出符号性的对应陈述(‖代表集合的基数)。由决策属性集D形成的划分设为U/D={D1,D2,…,Dm}， 其具有m个决策类Dj(j=1,2,…,m)。 条件属性子集A⊆C导出的等价划分为U/A={A1,A2,…,AN}， 其具有N个条件粒Ai(i=1,2,…,N)， [x]A代表着包含x的条件粒。当粒Ai中的元素隶属于不同决策类，则称为不协调，该情况引发着决策表的协调性与不协调性[13]。

1.2 基于信息熵的决策树算法

信息熵起源于信息的相关理论，表征和刻画系统的不确定性。以此可构造经典的决策树归纳算法，包括ID3[7]、C4.5[8]。

定义1[7]决策分类U/D的信息熵定义为

(2)

其中，Pj=|Dj|/|U| 表示第j个决策类的概率。条件属性子集A形成的划分U/A的信息度量定义为

(3)

Gain(A)=info(D)-info(A)

(4)

基于式(4)，ID3算法构造决策树的核心思想在于先计算单个条件属性的信息增益，具有最大信息增益的属性作为检测属性，最后通过序列递归完成分类过程。而ID3算法存在属性偏移、不能处理连续型数据、精度低等缺点。针对ID3的上述问题，在ID3算法的基础上建立了另一种基于信息熵的决策树归纳算法(C4.5算法)。

定义2[8]条件属性集A对应的信息增益率定义为

(5)

其中

(6)

对于属性优选，C4.5算法主要采用式(5)的信息增益率，其将信息增益规范化。从而，C4.5算法减少了属性偏移带来的影响，该模型的分类结果更好。同时，C4.5算法可以离散化连续属性，为后续的粒化分析与知识获取奠定基础。

1.3 基于属性依赖度的决策树算法

在粗糙集理论中，属性依赖度是关于近似推理的一个基础概念，用于描述条件、决策粒化之间的派生关联关系。由此，以属性依赖度为基础的相关决策树算法可以被提出。

定义3[13]决策类Dj基于条件属性子集A的上下近似定义为

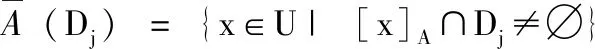
(7)

决策分类U/D关于A的分类正域与属性依赖度分别定义为

(8)

γA(D)=|POSA(D)|/|U|

(9)

在粗糙集中，上近似和下近似分别从两个方向对决策类进行近似逼近，可进行分类的样本包含于分类正域中，具有定性特征；进而，属性依赖度表征了相关的分类能力，但其量化形式主要对应于定性实质。基于粗糙集的决策树归纳算法(简记为RS)[17]，主要是通过选择依赖度最大的属性作为决策树的分裂节点。但如果后续条件属性的依赖度都为0，则替代采用ID3、C4.5中的信息增益与信息增益率作为检测属性的度量函数。经过反复迭代，直至叶节点属于一个决策类或所有条件属性都成为分裂节点。

2 基于属性纯度的决策树归纳算法

信息熵刻画粒结构的不确定性信息，属性依赖度是对知识的代数推理进行描述。因此，基于属性依赖度的决策树算法在分类能力的表达上具有优势。但是，条件粒化不协调于决策粒化或样本噪声影响，条件粒存在不归属于任意决策类的情况；在这种不协调的情况下，基于粗糙集的决策树算法一般复合使用信息熵的特征选择。机制准则不同的两种度量结合会导致分类效果的下降。对此，接下来将发掘一个关于分类精度的度量——属性纯度，当依赖度的特征选择失效时对其补充确定分裂节点，使得该类决策树算法不再受限于度量函数的复合使用并具有较好的分类能力。鉴于此，决策表DT中单属性c∈C及其诱导的知识划分假设为

U/{c}={{c}1,{c}2,…,{c}n}

2.1 三层纯度与属性纯度

定义4 若∃Dj∈U/D使得{c}i⊆Dj， 则条件粒 {c}i∈U/{c} 称为绝对纯的。若∀{c}i∈U/{c} 是绝对纯的，则条件属性c称为绝对纯的。

命题1：条件属性c是绝对纯的，当且仅当γ{c}(D)=1。

条件粒化和决策粒化之间的交叠派生关系是知识推理、识别分类的粒计算底层机制，而绝对纯性直接代表相关的识别过程。换句话说，粒 {c}i是绝对纯的，其完全包含于一个对应的决策类Dj， 可被完全识别。条件属性c是绝对纯的，该属性生成的所有粒结构都可以被相应的决策类识别；对此，属性依赖度达到最大数值，即γ{c}(D)=1。 但这种定性识别下的纯性可能是理论上的，即条件属性通常意义下都不是绝对纯的；为此，需要定量的纯性测度来描述识别精度，从而表征γ{c}(D)<1的一般情况与γ{c}(D)=0的特殊情况。下面提出条件粒关于决策类的纯度概念。

定义5 给定条件粒 {c}i∈U/{c} 与决策类Dj∈U/D。

(1) {c}i关于Dj是绝对纯的，若 {c}i⊆Dj；

(2) {c}i关于Dj是绝对不纯的，若 {c}i∩Dj=∅；

(3) {c}i关于Dj是近似纯的，若 {c}i∩Dj≠∅且 {c}i⊄Dj。

特别地， {c}i关于Dj的纯度定义为

(10)

粒 {c}i和决策类Dj的交互重合部分占 {c}i的比值称为纯度，代表粒 {c}i被决策类Dj的识别程度，及对应分类决策 {c}i→Dj的可信度。这一度量能够有效支撑相关的定性理解。显然， Pure{c}i(Dj)∈[0,1]。

(1)若Pure{c}i(Dj)=1， 则 {c}i关于Dj是绝对纯的；

(2)若Pure{c}i(Dj)=0， 则 {c}i关于Dj是绝对不纯的；

(3)若Pure{c}i(Dj)∈(0,1)， 则 {c}i关于Dj是近似纯的。

定义5提供的条件粒与决策类的纯性可以描述定义4的条件属性的纯性及相关概念。例如，条件属性c是绝对纯的，当且仅当∀{c}i∈U/{c}， ∃Dj∈U/D， 使得 {c}i关于Dj是绝对纯的；此外，还可以基于条件分类U/{c} 来定义并刻画条件属性c的近似纯性。特别地，定义5提供的纯度为后续属性度量构建奠定了基础。下面，基于决策表的三层粒结构[18]实施三层构建来定义三层纯度，包括决策树需要的属性纯度。

定义6 粒 {c}i关于决策属性D的纯度定义为

(11)

其中，属性c关于决策属性D的纯度定义为

(12)

命题2：三层纯度具有如下集成关系

(13)

鉴于决策表的三层粒结构[18]，式(10)～式(12)建立了三层纯度体系，而式(13)则反映了三层纯度之间的相互集成关系。

(1)纯度Pure{c}i(Dj) 位于微观底层 ({c}i,Dj)， 表征 {c}i关于Dj的识别能力。

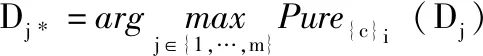
(3)纯度Pure{c}(D) 位于宏观高层 (U/{c},U/D)， 统计求和n个中层纯度Pure{c}i(D)(i=1,2,…,n) 以达到集成目的，用以表示U/{c} 关于U/D的识别性。

最终得到的纯度Pure{c}(D) 通过量化属性c关于决策类U/D的识别能力，从而建立了一种分类识别的机制。对此，该高层纯度可以重新定义为“属性纯度”以反映其对条件属性的直接选择功能，即可作为决策树归纳算法中分裂节点的相关度量函数，以保障模型的分类精度。后一节中，属性纯度直接作为决策树归纳算法中的节点度量函数，并取得较好的分类效能。

对于上述三层纯度和属性纯度，用一个示意图对相关构造和意义进行深入分析、解释。如图1所示，中间含有竖线的长方形表示非空有限的论域U， 对称的左右两个正方形代表决策属性形成的两个决策类U/D={D1,D2}。 3个不同的阴影横带表示U/{c}={{c}1,{c}2,{c}3} 的3个条件粒。

图1 纯度

(1) {c}1,{c}2,{c}3与D1,D2均相交，微观底层 ({c}i,Dj) 共有6个纯度。其中粒和粒交叠最大者是{c}2∩D2，但和{c}2的比率不大(由于{c}2和D1也有重叠部分)，该纯度反映粒{c}2识别能力不强。相反，{c}1∩D1和{c}1的比值近似1，表明粒{c}1中样本绝大多数也在D1中，故该高纯度值对应相应的高分类识别能力，也表征决策规则{c}1→D1的高精确度。

(2)在中观中层({c}i,U/D)的极大统计中，{c}1,{c}2,{c}3分别与D1,D2,D1产生最大纯度，故获得图中标识的3个纯度

(3)在宏观高层(U/{c},U/D)中，把上述中层统计量“加和”集成得到

Purec(D)=Pure{c}1(D)+Pure{c}2(D)+Pure{c}3(D)=
Pure{c}1(D1)+Pure{c}2(D2)+Pure{c}3(D1)

该纯度描述基于条件分类U/{c}={{c}1,{c}2,{c}3}与决策分类U/D={D1,D2}的系统分类性能，故表征属性c关联于数据分类的重要性程度。

2.2 基于属性纯度的决策树算法

命题3： Pure{c}(D)≤n， Purec(D)=n⟺γc(D)=1。

属性纯度以n为上确界，命题3反映了该上确界的等价条件。属性依赖度的最大值和属性纯度的最大值有着对应关系，说明二者之间的关联性。

下面分析阐述信息熵、属性依赖度和属性纯度之间的机制关系，从而为提出合理的决策树算法奠定基础。就公式而言，信息熵描述不确定性信息，属性依赖度和属性纯度则是知识的代数推理，故体系机制上是不同的，称为异质的。关联于分类模型的精度追求，重点剖析后两者。属性依赖度是对正域的定性描述，是定性分析度量；对比地，属性纯度统计集成于三层纯度的定量识别性，是定量分析度量。因此，属性依赖度和属性纯度是同质异态的，并有着最值关联性(命题3)，二者和信息函数是异质的。由此机制，下面构建一个合理的决策树算法，即DP(dependency-purity)算法。针对依赖度保障分类精度的主体作用，DP算法以“先属性依赖度定性、后属性纯度定量”的二级选择策略将属性排序，实施特性选择过程。DP算法有着分类能力上的优势。

(1)和RS算法类似，DP算法先用属性依赖度定性优选条件属性，依赖度数值均为0时则引入同质的属性纯度补充，这确保了对分类能力的一致追求，故体现出有效性。

(2)和C4.5算法对比而言，DP算法使用的二级度量函数都持续且一致地追求分类精度，故比C4.5算法更有分类能力上的优势。

算法1： DP算法

输入： 一个决策表DT

输出： 决策树

(1) ∀c∈C， 计算γ{c}(D);

(2) if ∃γ{c}(D)≠0 then

(4) else

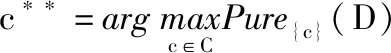
(6) end if

(7) 分裂节点在DT中诱导出知识分类

U/{c}={{c}1,{c}2,…,{c}n};

(8) for ∀{c}i∈U/{c}

(9) 分别取 {c}i中的样本将DT分割为子决策表

DT1,DT2,…,DTn;

(10) end for

(11) 对于决策表DT1,DT2,…,DTn， 递归地进行第 (2)～ (10) 步， 直到所有条件属性都被检测或者样本均包含于同一个类为止。

(12) 返回决策树。

DP算法先使用属性依赖度从知识粒化分析的角度定性保障决策树的分类精度，发生不协调的问题时，再通过属性纯度维持知识推理的过程及分类效果。具体而言，步骤(1)～步骤(3)计算所有属性的依赖度，通过数值排序，选择具有最大值的属性作为决策树的分裂节点，使得决策树模型结构简单且精度较高。若出现不协调情况，依赖度数值均为0，步骤(4)～步骤(6)计算所有属性的属性纯度，选择具有最大值的属性作为决策树的分裂节点，避免使用异质的信息函数降低模型的分类效能。步骤(1)～步骤(6)实现了节点的二级选择，后面的过程与传统的决策树构造方法一致，步骤(7)～步骤(11)用优选的分裂属性将决策表分割成多个子表，通过对这些子决策表递归前面的操作流程，最后得到一个决策树模型。

3 实例分析

这里提供一个实例决策表，见表1。其中D表示1个决策属性，并具有5个条件属性和15个样本。使用3种决策树归纳算法构造决策树，即基于信息熵的算法C4.5[8]、基于粗糙集的算法RS[17]以及本文的算法DP，相关树形结构如图2所示。下面阐述对应算法的实施过程并分析相应结果。

表1 实例决策

首先考虑C4.5算法。每个属性的信息增益率为gainratio(c1)=0.0292，gainratio(c2)=0.1088，gainratio(c3)=0.1686，gainratio(c4)=0.0292，gainratio(c5)=0.0850。

属性c3有着最大的信息增益率数值，故选为第一个节点。通过该属性决策表可分为两个子表，递归过程，最终如图2(a)的决策树模型即可得到。从图2(a)中可以看到，属性c4在被选为分裂点后，因为gainratio(c1)=0.0248，gainratio(c2)=0，gainratio(c5)=0.0728。

图2 3种算法构造生成的决策树

c5具有最大的信息增益率，将c5作为下一个分裂节点。关于最终结果，所建决策树的叶子数为8，其中只包含一个样本的叶节点个数为5。

分析RS算法。 ∀i∈{1,2,3,4,5}，γ{ci}(D)=0， 每一个条件属性的依赖度值为0，出现不协调性。此时，需要转为求助信息增益率。因此，该算法和基于信息熵的算法有着相同的树形结构，如图2(a)所示。这体现RS算法以属性依赖度为度量函数的缺陷。

最后解释DP算法。先计算出三层纯度值，见表2。而条件属性是二分类的 (n=2)， 决策类也是二分结构 (m=2)

D1={x1,x2,…,x7}，D2={x8,x9,…,x15}。

对此，一个属性应具有4种底层纯度，向上最大取样后还有两种中层纯度，最终再向上集成出一种高层纯度(即属性纯度)。以表2关注到属性纯度，进行相关特性选择输出决策树。5个条件属性的纯度为Pure{c1}(D)=1.2500，Pure{c2}(D)=1.4000，Pure{c3}(D)=1.5000，Pure{c4}(D)=1.2500，Pure{c5}(D)=1.3933。

表2 实例决策表的三层纯度

选择具有最大纯度的属性c3作为第一个分裂节点。对分裂后的子表进行类似的递归操作，即可输出一个如图2(b)的决策树。该模型的叶子数为7，其中只包含一个样本的叶节点个数为3。

针对图2(a)和图2(b)两个模型之间的差异，可以体现DP算法的改进性。而DP算法的构建流程中，在属性c4作为分裂节点后，具有最大纯度的c2将作为下一个分裂节点，因为Pure{c1}(D)=1.2143，Pure{c2}(D)=1.3333，Pure{c5}(D)=1.3000。

这个过程与上述C4.5算法、RS算法中的 “c4后选c5” 有所不同。对比C4.5算法、RS算法，DP算法生成的决策树叶子数从8减少为7，只含有一个样本分类的叶节点个数也相应从5降低为3。由此可知，DP算法构建的模型结构更简单；由于不同的分类规则有更多的样本支持，故DP算法的决策分类能力也得到提升。总之，本例结果表明，DP算法比C4.5算法、RS算法更加优越。

4 数据实验

这里依托UCI数据库进行数据实验，实施C4.5算法[8]、RS算法[17]、DP算法、ID3的改进算法(NID3)[12]来构建4种决策树，并通过对比分析来验证DP算法的有效性与优越性。

这里采用UCI机器学习库[19]中的7个连续型数据集，相关的决策表信息见表3。所有的数据集都只具有一个决策属性；部分数据有缺失值，这里删除具有缺失值的对应样本；而FM数据集一共有60种决策分类，主要截取前4个决策类中的样本实施实验；采用C4.5算法[8]对7个数据集进行离散化预处理。

表3 7个UCI数据集的决策表信息

针对每种数据集，分别采用C4.5算法、RS算法、DP算法、NID3算法来构建4种决策树模型，并主要采用准确度与叶子数两类评估指标。此外，把7个数据集的结果进行统计，提供准确度与叶子数的算术平均值。相关决策树结果见表4。针对同一数据集，记号*标识获得一致决策树结构的算法，而记号**标识4种算法中的相关最优值。为形象分析，表4中的准确度与叶子数还分别用图3、图4标识出来。

基于表4及图3、图4的结果，可以从准确度与叶子数两个角度来对比分析C4.5算法、RS算法、DP算法、NID3算法。在Iris数据集中，4种算法生成的决策树的结构是完全相同的；此外，在Wine数据集中RS算法与DP算法也给出一致结构。关于分类准确度：

图3 4种决策树算法的准确度对比

图4 4种决策树算法的叶子数对比

表4 4种决策树算法关于准确度与叶子数的实验结果

(1)对于Glass数据集， DP算法具有明显优势，即显著优于C4.5算法、 RS算法、 NID3算法。对于FM， DP算法的分类准确度最高，且显著优于NID3算法；

(2)对于Iris、Wine，RS算法具有最优化准确度，DP算法与RS算法具有一致决策树结构从而具有一致分类能力。同时， DP算法取得第二的优势，且与最优的RS算法非常接近；

(3)对于剩余的BCC、ILPD、Wpbc，NID3算法具有最优的准确度，此时DP算法取得第二的优势。同时， DP

算法结果与NID3算法的差距并不明显，但却明显优于C4.5算法、 RS算法。

关于叶子数：

(1)对于Iris、Wine，DP算法是最优的(或共同最优)；

(2)对于Glass，RS算法取得最优叶子数，而DP算法具有一个中间的叶子数且与RS算法结果靠近；

(3)对于FM，C4.5算法取得最优叶子数， DP算法取得第二优且与C4.5算法结果很接近；

(4)对于BCC、ILPD、Wpbc，NID3算法具有最小的叶子数，但DP算法的结果也是靠近NID3算法的。

最后从表4的平均统计来看， DP算法的分类精度比较显著地优于C4.5、RS、NID3；此外，DP算法的叶子数处于第二优的位置，即其略逊于RS算法的最优值但优于剩余的C4.5与NID3。综上结果与分析可见， DP算法是有效的，总体上具有比C4.5算法、 RS算法、 NID3算法更好的决策树分类结果。

5 结束语

剖析基于依赖度的决策树归纳算法存在的不协调与度量转换问题，提出属性纯度并由此构建决策树归纳算法DP。首先，属性纯度来源于识别刻画与三层构建，其与经典决策树分裂属性度量函数既有联系又有区别。信息函数描述粒化结构的不确定信息，主要采用信息观点；属性依赖度与属性纯度直接从代数角度表征识别精度，但分别关联于定性区域与定量统计；可见，属性依赖度与属性纯度异质于信息熵，而两者具有不同的定性定量形态，即两者是同质异态的。由此度量机制， DP算法具有先属性依赖度后属性纯度的二级联动机制，有效改进了C4.5与RS两种存在的决策树归纳算法。实例分析与数据实验均验证了DP算法的有效性与改进性。属性纯度以及三层纯度还值得深入研究， DP算法也值得广泛推广以获取实际应用效能。