基于耦合模拟退火S3VM的信用预测
2021-01-20王国伟
李 琳,王国伟,张 杰,周 栋
(1.武汉理工大学 计算机科学与技术学院,湖北 武汉 430070;2.湖南科技大学 计算机科学与工程学院,湖南 湘潭 411201)
0 引 言
在线P2P(Peer-to-Peer)贷款[1],又称为点对点贷款,为民间小额借贷,方便了小微企业的借贷。在实际生产生活中,许多小微企业经常需要小额短期资金进行周转,但银行借贷的过程复杂,无法满足小微企业的需求[2,3]。
借贷行业的实际情况给模型训练带来了困难,导致信用预测结果的准确度偏低。首先对于训练数据样本的形成,仅当金融机构完成了某次借贷申请流程后,才会形成标记数据。大多小微企业无信用记录,仅有少量小微型企业的信用被相关的金融机构评估。人工标记数据的成本过高导致训练样本严重不足。可以看到用借贷历史记录作为训练数据集,不但标记数据量少,且其正负样本比例不均衡,传统的监督机器学习方法的预测效果会因此受到影响。
半监督学习充分利用未标记数据中的信息,提高模型在预测时的表现。简单而言,半监督学习可将一些不含标签的数据通过一定的机制添加到训练数据中,用以缓解上述问题。
基于半监督支持向量机的信用评估是一种有效的预测方法[4]。由于超参数通常由经验选取,当对不同数据集进行预测时,由于数据集间的差异,无法保证模型的稳定性。因此,本文提出基于耦合模拟退火的S3VM(CSAS3VM),采用耦合局部最优的方法来优化模拟退火过程,寻找半监督支持向量机的最优参数。实验结果表明,本文提出的CSAS3VM,具有更高的精度和较高的F-1值,且在正负样本比例不均衡时也表现稳定,是一种有效的信用预测方法。
1 相关工作
1.1 信用评估
对于信用评估,主流机器学习方法已有较好的表现。Malini等[5]提出了基于KNN和离群值检测的信用卡欺诈识别模型;Save等[6]提出了一种使用决策树(decision tree)检测信用卡交易处理中欺诈行为的系统。支持向量机同样被广泛应用于信用评估。Yu等[7]试图提出一种基于深度置信网络的重采样SVM集成学习范式,并将其用于信用评估;肖斌卿等[8]使用最小二乘SVM,建立了用于小微企业的信用评估模型;Hsu等[9]的研究结果表明将SVM与人工蜂群方法相结合,能够提高信用评估的结果。
除传统的机器学习方法外,神经网络也同样受到关注。Oresk等[10]提出了一种神经网络混合遗传算法(HGA-NN),用于提高信用评估的分类准确性和可扩展性。Fu等[11]提出了一个基于CNN的信用欺诈检测框架,从标记数据中学习欺诈行为的内在模式。
监督学习方法中SVM在信用评估上表现突出,本文在半监督SVM中引入耦合模拟退火机制优化参数选择,提升信用预测质量。
1.2 半监督学习
在21世纪初,半监督学习得到广泛关注,主要有生成式、基于图的半监督、协同训练和半监督支持向量机等[12-14]。本文主要关注半监督支持向量机,其基本思想是:将未标记的信用数据加入到模型中,试图找到划分超平面能对数据进行分类且穿过的区域为数据稀疏区域。Chen等[14]对Lap-TSVM进行改进,提出了Lap-STSVM,将原始约束转换为无约束最小问题;Rethishkumar等[15]利用分支定界法优化的确定性退火半监督支持向量机(DAS3VM)对节点进行分类;Huang等[16]将基于流形正则化的极限学习机扩展到半监督和无监督任务中;Dai等[17]提出了一个基于对抗生成网络的半监督学习框架,该框架使用生成的数据来提高任务性能;Wang等[18]提出了一种基于主动学习结合TSVM的新型半监督学习算法,并在目标函数中添加流形正则项;Yang等[19]提出了一种基于图嵌入的半监督学习框架,并与基于高斯调和函数的半监督方法进行了对比。
在信用预测和金融风控领域,考虑半监督学习方法来解决标记数据不足问题的研究偏少,Li等[20]的研究结果表明半监督支持向量机在信用预测上比逻辑回归表现好;Lebichot等[21]提出了基于图的半监督信用卡欺诈检测系统。
1.3 演化算法与半监督学习
演化算法的灵感源于自然界生物的进化,其在参数优化、模式识别和机器学习等众多领域有较为广泛的应用。Chen等[22]的MPSVM是一种用于半监督分类的支持向量机,并采用粒子群算法来优化模型参数的选择;Albinati等[23]提出基于蚁群算法的半监督分类算法;Lazarova等[24]使用遗传算法与S3VM结合,提出GS3VM来优化非凸问题,在Diabetes和Coil20数据集上表现出较好的结果;Lazarova等[25]提出了一种半监督多视图遗传算法,应用于回归函数学习中。根据上述文献,将演化算法与半监督相结合的方法能有效提高传统半监督方法的准确性并且现有的研究工作对所采用的传统演化算法做了进一步优化和改进。总体上,实验中除了与传统的半监督方法对比之外,还对比了所要改进的演化方法。
本文考虑到基于确定性退火的S3VM(DAS3VM)采用人工选择参数[15],模型容易过拟合或欠学习,而基于模拟退火的S3VM信用预测方法[26]受初始温度影响,低温时容易陷入局部最优。针对该问题,本文提出了耦合模拟退火的S3VM方法,通过共享多个模拟退火过程的信息,优化模型参数的选择。本文利用耦合模拟退火优化半监督的参数学习,今后的研究将考虑其它演化算法在实际问题中的可行性。
2 耦合模拟退火半监督SVM方法
本文研究演化算法与二分类的S3VM结合,寻找模型的优化参数,以此来提高分类预测效果。
2.1 确定性退火半监督SVM(DAS3VM)


(1)

确定性退火半监督支持向量机(DAS3VM)[15]通过构造一个关于温度T的自由能函数,将传统的S3VM的最优化过程转换为一系列温度依赖的物理系统。其中pj∈[0,1], 是x′j在正类上的概率。将变量uj放大到概率变量pj, 并根据pj建立关于温度T的函数,如式(2)所示

(2)
式(2)中,r为正样本在所有样本的占比,T控制了一系列目标函数。从式(2)的优化中得到最优解的过程转换为温度T的降温过程,从高温状态逐渐降低,理想值为0。记录函数最值,由此获得最优解。温度转移的过程为Tk=ρTk-1,Tk模拟退火的过程中,第k次的温度,ρ为过程中的系数。初始状态下,温度降低较快,随着降温过程的进行,退火速度逐步减慢。
2.2 耦合模拟退火半监督SVM(CSAS3VM)
2.2.1 耦合模拟退火
SVM超参数选取,对算法最终表现有较大影响[27]。确定性退火S3VM是根据经验或实验测试来选择。本文提出的耦合模拟退火S3VM,将耦合模拟退火用于到S3VM的超参数选取。耦合模拟退火(coupled simulated annealing,CSA),模拟物理过程中的退火,在初始状态下求解全局最优解[28]。耦合模拟退火(CSA)与单个退火求解和并行多个退火求解问题的差异在于其将多个退火过程中的状态信息共享,通过耦合的方式定义接受概率,面对新状态的到来,所有耦合信息共同决定温度状态是否转移。
对于新状态的接受概率A(s→st), 数学上有多种定义。本文在寻求最优解的过程中,采用的是Metropolis规则的变形,如式(3)所示
(3)
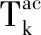
(4)
利用Boltzmann求解系统在第i个状态的概率值,假设 (i=1,2), 即系统仅有两个可选状态,如式(5)所示
(5)
式(5)中kB为Boltzmann常数,Ei为i状态下,当前系统的能量值,T为i状态下的温度。Z为当前系统所有状态的能量和,如式(6)所示
(6)
考虑式(4)和式(5),在状态st和温度T已给定的情况下,状态st被接受的概率值由式(5)近似表示。为了实现耦合模拟退火,先初始化一个多状态系统,s为状态的集合,si为当前的第i个状态,sti为第i个当前状态将要转移的新状态。设s∈{s1,s2,…,sm}, 式(4)转换为式(7)
(7)

此时,当前状态s∈{s1,s2,…,sm} 对应新状态st∈{st1,st2,…,stm} 的接受概率为A(s→st)∈{A(s1→st1),A(s2→st2),…,A(sm→stm)}。 状态集合s内各个状态接受对应的转移状态st的概率,除了考虑自身外,还要考虑其它状态的耦合。特殊情况下,当状态总数m=1时,方法将退化为传统的模拟退火求解问题。
定义Θ={s1,s2,…,sm}, Θ⊂Ω, Ω为所有合法状态的集合,CSA中的状态si转移到新状态sti的概率如式(8)所示
0≤AΘ(γ,si→sti)≤1
(8)
当前状态si∈Θ, 新状态sti∈Ω,γ为耦合项,如式(9)所示
γ=f[E(s1),E(s2),…,E(sm)]
(9)
如图1所示,可以看到CSA与SA的主要不同点在于接受概率的定义。它使得当前状态集合下所有SA的状态信息共享,并对耦合项和接受概率进行组合,寻找全局最优解。

图1 模拟退火与耦合模拟退火的区别
2.2.2 CSAS3VM方法描述
耦合模拟退火半监督支持向量(CSAS3VM)将耦合模拟退火应用于寻找半监督支持向量机的最优参数。设定初始值,由此生成当前状态。通过扰动函数,产生新状态。关于扰动函数的定义请参见文献[26],扰动因子ε的分布为
(10)
将式(10)带入扰动函数,由此新状态st的表达式如式(11)所示
(11)
具体实现如算法1所描述,源代码见https://github.com/WUT-IDEA/SAS3VM(含传统模拟退火方法和耦合模拟退火方法)。
算法1:CSAS3VM
输出:全局最优解ω

(2)对集合Θ的每个状态si都通过扰动函数产生新的状态sti=si+εi, ∀si∈Θ。εi是通过式(10)随机得到的变量。将转移状态sti和当前解ωi作为输入,代入算法2中,计算转移状态的能量E(sti), ∀sti∈Θ, ∀i=1,2,…,m。
(3)对每个i=1,2,…,m, 如果E(sti)≤E(si), 接受新状态sti; 否则,以AΘ(γ,si→sti) 的概率,接受转移状态sti。 当AΘ>δ时,接受转移状态sti,δ∈[0,1]。 更新每个SA对应的当前最优解ω*, 计算耦合项γ, 返回步骤(2),循环N次。

(5)如果达到预先设定好的停止条件,则算法结束,找到能量E(si),i=1,2,…,m的最小能量,输出该能量所在状态的最优解ω*; 否则,从步骤(2)开始,继续循环。
CSAS3VM的时间复杂度为O(nNE),N为CSA方法内循环次数需要的次数,n为CSA方法外循环次数需要的次数,E为计算系统能量E(s) 的时间复杂度(算法2中给出计算)。
本文提出的CSAS3VM的接受概率如式(7)所示,使得接受新状态的概率AΘ(γ,si→sti) 与转移状态的能量E(sti) 成反比。耦合项由当前所有状态共享。
传统的确定性退火半监督支持向量机中的超参数λ和λ′, 常见的做法是通过经验判定。就不同的数据集,超参数初始化不同,会影响预测结果。针对该情况,本文在寻找实际问题中最优参数组合时,选定初始值后,第k次的超参数的扰动函数如式(12)所示
λk=λk-1+εk-1λk∈Ω
(12)
εk-1为满足式(10)的随机变量。
接下来讨论使用确定性退火(DA)计算系统能量E(s) 的过程,见算法2。
算法2:E(s)计算
输入:状态s, 当前最优解ω;
输出:当前状态能量E(s), 最优解ω。


(3)使用拉格朗日方程,将式(2)重构为式(15),求pj的偏导,带入到式(2)的约束后,得到用于求解拉格朗日乘子v的非线性方程,通过使用组合的牛顿-拉夫逊迭代法和二分法进行求解。计算v, 更新pj。
(4)循环执行步骤(2)和步骤(3),对ω和p进行优化,检查是否满足停止迭代的条件。本文采用pj的当前值p与上一次循环的值q的平均KL距离。
(5)对Tda进行降温,将改变后的ω作为传统监督SVM的初始值,重复步骤(2)~步骤(4),当温度为最低或者达到最大循环次数时,停止。
(6)更新ω, 使用测试集,完成当前状态s的能量E(s) 的计算。

(13)


(14)
步骤(3)中构造的式(2)的关于拉格朗日方程如式(15) 所示

(15)
式(15)中,v为拉格朗日pj乘子,对pj求偏导得到式(16)

(16)
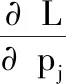
pj代入到传统监督SVM的约束条件得到式(17)
(17)
式(17)为关于v的非线性方程,通过算法2的步骤(3),带入式(17)可以得到pj。
本文中的KL距离定义如式(18)所示
(18)
当满足KL(p,q) 本文使用的两类数据集分别是UCI(https://archive.ics.uci.edu/ml/datasets.html)公开的个人信用数据(德国、澳大利亚、日本)和通过网络爬取的中国企业信用数据(credit-one、credit-two)。 表1为UCI上的3组个人信用数据集的相关信息。p+n项为数据集的样本数,p为正类样本,n负类样本,feature为每个样本的特征数量。 表1 个人信用数据集 由于UCI的信用数据集来自于90年代且数据量偏小,本文通过爬虫从阿里巴巴(https://s.1688.com)和企业信用信息公示系统(http://www.gsxt.gov.cn)中爬取企业信用相关数据。由于数据存在缺失,还需要对数据进行筛选。 筛选后,形成两个企业数据集credit-one和credit-two。相关字段的意义与表1相同,见表2。credit-one数据集属于正负样本不均衡,而credit-two数据集相对均衡,本文根据这两种数据的实验结果讨论不同信用预测方法的性能。 表2 企业信用数据集 本文所有需要用到核函数的算法,选取的核函数为线性核。提出的CSAS3VM方法与以下7种方法进行了对比实验:基于传统监督学习的方法(1)和方法(2)与基于半监督学习的方法(3)~方法(7)。 (1)RLS[29]:逻辑回归,监督学习方法。 (2)L2-SVM-MFN[30]:传统支持向量机,监督学习方法。 (3)TSVM[18]:半监督支持向量机,半监督学习方法。 (4)HF[19]:基于高斯调和函数的半监督算法,半监督学习方法。 (5)NBEM[31]:朴素贝叶斯最大期望算法,半监督学习方法。 本文提出的CSAS3VM是在确定性退火和模拟退火S3VM上的改进。 (6)DAS3VM[15]:用确定性退火寻找最优解的半监督支持向量机,半监督学习方法。 (7)SAS3VM[26]:用模拟退火寻找最优解的半监督支持向量机,半监督学习方法。 (8)CSAS3VM:本文提出的耦合模拟退火半监督支持向量机(使用 L2-SVM-MFN 在标记数据上训练出一个初始分类器),半监督学习方法。 为避免实验中出现过拟合现象,本文采用反K折交叉验证的方式,该方式为半监督学习中常用的验证方式,使结果更加真实准确。反K折交叉验证的过程类似于K折交叉验证,不同点在于训练数据和测试数据划分的方式。反K折交叉验证在训练过程中一次选择1折进行训练,其余K-1折数据为测试数据,最后取K次实验的平均结果。实验中,设置K=5,10,20,30,40,50,60,70,80,90,100。 本文的评价指标包含:分类的精度(Precision)、召回率(Recall)和F-1值(F-1 scores)。F-1值对精度和召回率进行了权衡。精度(Precision)表示分类器预测为正的样本中,预测准确的比例。召回率(Recall)表示测试集中正样本被预测出的比例。在信用评估中,信用为负的个人或者企业若被误分,将获得贷款,这将带来非常大的经济损失。所以本文除了考虑评价指标F-1值,还关注各种方法在精度指标上的表现。 图2(a)、图2(b)用折线表示8种方法在企业信用数据集上精度对比的实验结果,图2(c)~图2(e)则是在个人信用数据上的对比结果。横坐标表示反K折交叉验证中K的不同取值,K越大,则表示标记数据越少,越能体现半监督学习类方法的优势。 图2 精度对比实验 在credit-one和credit-two企业信用数据集上(图2(a)、图2(b)),本文所提出的CSAS3VM方法精度明显最高。以credit-one的数据为例,当K=5时,半监督方法中DAS3VM的精度为77.3,HF为83.6,本文提出的CSAS3VM为92.4;当K=100时,标记数据只有1折数据,SAS3VM的精度为74.1,HF为79.3,本文提出的CSAS3VM为92.8。在credit-one数据集上,取不同K值时,各方法的精度见表3。 表3 credit-one数据集上的Precision值/% 从企业信用数据的实验结果总体来看,半监督学习类方法优于监督类学习方法RLS和L2-SVM-MFN。CSAS3VM方法将较少的负类样本预测为正类样本,具有最高的精度。当数据正负样本不均衡时,CSAS3VM方法在精度指标上表现稳定,而其它方法的精度在credit-one上明显低于credit-two。 图3(a)、图3(b)为在不同K值下,8种方法在企业信用数据集上召回率的对比结果,图3(c)~图3(e)为个人信用数据集上的对比结果。 图3 召回率对比实验 在credit-one、credit-two数据集和德国数据集上,CSAS3VM的召回率表现并不理想,这是由于CSAS3VM不只是关注预测正例的效果。而NBEM方法在德国数据集上部分K值的召回率达到了100%,这是因为数据集正负样本不均衡,其中德国数据集的正例样本占比为70%,算法偏向于将样本预测为正例,忽略了在信用评估领域若负例被预测为正例会造成较大的损失。在澳大利亚和日本的个人数据集上,CSAS3VM方法在大部分K值上召回率为最高。 在信用评估中,应更加关注精度(预测信用为好的样本中,实际信用好的样本所占比例)。因此,仅通过召回率来评价模型并不合理,综合了召回率和精度的F-1值能更好评价算法的表现。 图4(a)、图4(b)用折线表示8种方法在企业信用数据集上F-1值的对比实验结果,图4(c)~图4(e)则是在个人信用数据上的对比实验结果。 图4 F-1值对比实验 在credit-one和credit-two企业信用数据集上,本文提出的CSAS3VM方法的F-1值最高,其次是SAS3VM方法。 在credit-one数据集上,由于其不均衡,其它非退火类方法随着K值的变大,性能下降明显。在credit-two数据集上,CSAS3VM方法明显优于其它7种方法,当K=100时,CSAS3VM方法的F-1值为65.4,比次之的SAS3VM(60.3)提高了8.5%,比监督方法中表现最好的L2-SVM-MFN(56.1)提高了16.6%。 以credit-one数据为例,当K=5时,本文提出的CSAS3VM的F-1值为83.0,次之的L2-SVM-MFN监督方法为82.4;两者差距不大,是因为有1/5的训练数据参与训练。当K=100时,标记数据只有1/100份时,CSAS3VM的F-1值为81.4,而L2-SVM-MFN监督方法为76.8。可以看到随着K值的增大,训练数据越来越少,本文提出的CSAS3VM方法表现稳定且最优。NBEM方法表现最差,波动较大。 在个人信用数据集上,本文提出的CSAS3VM方法在F-1值上表现稳定,特别是在K取值较大的情况下,其次是SAS3VM。以澳大利亚个人信用数据集为例,当K取值小于等于20时,SAS3VM的F-1值稍微高于CSAS3VM方法,最多为1.6%;但是当K取值大于20之后,CSAS3VM方法明显优于SAS3VM,最高提升了7.9%。总体而言,和其它方法相比,耦合模拟退火方法在参数寻优方面表现突出。 NBEM方法表现最差,虽然在德国个人信用数据集上有82左右的F-1值,其原因是NBEM方法简单,算法倾向于预测多数类,即将数据预测为正类。由此得到了接近100%的召回率和70%左右的精度;而在澳大利亚和日本数据集上的F-1值不足50。 (1)本文提出的CSAS3VM方法在两种共5组数据集上的总体表现最好,精度最高,F-1值较高。在正负样本比例不均衡时,也表现稳定。可以看到耦合模拟并行地进行模拟退火过程,通过接收概率函数耦合,提高了最优参数搜索的性能,弥补了传统模拟退火方法对初始参数选取鲁棒性差的缺点。 (2)引入模拟退火机制的S3VM,比如本文提出的CSAS3VM和已有的SAS3VM,综合来看均比其它方法表现好。较差解在满足条件的情况下,模拟退火将接受该解,避免算法一直处于局部最优。 (3)半监督的HF和NBEM方法总体上看表现最差,大多数情况下也不如RLS和L2-SVM-MFN两种监督学习方法。与大多数的研究结果一致,SVM分类预测能力强。 (4)监督学习方法RLS和L2-SVM-MFN随着K的增加,训练数据减少,精度减少,F-1值减少,预测性能呈现明显的下降趋势。可以看到监督学习方法在训练数据小于测试数据的情况下,性能不理想。 本文在传统半监督支持向量机的基础上,提出了CSAS3VM,并在5组数据集上进行了对比实验。综合精度、召回率和F-1值3项评价指标,本文提出的CSAS3VM相对于SAS3VM和其它方法,具有更高的精度和较高的F-1值。因此,可以认为CSAS3VM是一种有效的信用预测方法,在正负样本不均衡的情况下,表现稳定。 CSAS3VM在准确度和效率上都存在改进空间。耦合模拟退火虽然并行处理多个退火过程,但单个退火过程仍采用单次比较的方式。今后考虑在每一个当前状态,采用多次搜索策略,搜索当前状态范围内的最优解。其次,耦合模拟退火在多个模拟退火之间进行信息共享,这一特性让其适应于分布式环境,今后同样可以考虑在分布式环境下,实现CSAS3VM。3 实 验
3.1 数据集


3.2 对比方法
3.3 评价指标
3.4 精度对比实验
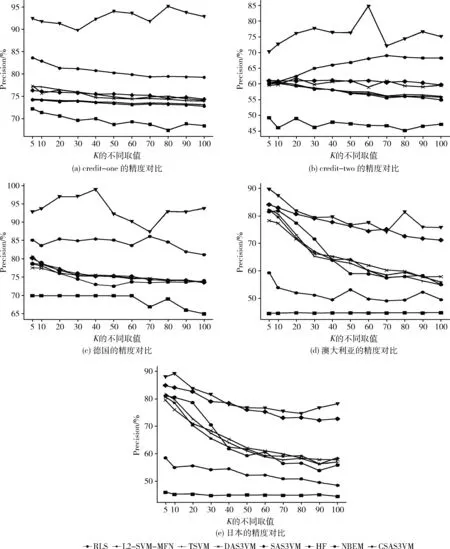

3.5 召回率对比实验

3.6 F-1值对比实验

3.7 实验结果分析
4 结束语
