基于向量相似性的多维标度定位算法

郑 天，冯秀芳

(1.太原理工大学 信息与计算机学院，山西 晋中 030600；2.太原理工大学 软件学院，山西 晋中 030600)

0 引 言

定位方法的研究目标是围绕降低定位服务成本、提高室内定位精度、适应复杂多变的室内环境等[1]。基于WLAN的室内定位方法主要有两种：参数化室内定位方法和非参数化室内定位方法[2]。

在参数化室内定位方法中，多维标度(multidimensional scaling, MDS)算法采用目标间的欧几里得距离作为相似性度量，当给定目标间的欧式距离之后，算法可以确定低维空间的相对位置。其中，石欣等将信号强度指示作为目标间的度量值构建相异性矩阵[3]。一些系统将多维标度算法与指纹定位相结合[4,5]，在离线阶段降低了指纹信息采集的开销，减少了所需参考点的个数。Parviainen M等在一种动态声学自定位系统中使用多维标度算法来映射节点位置[6]。一部分学者对多维标度算法进行了修正，缩小了最短路径与欧式距离的差异值，优化了节点间相关性关系并提高了定位精度[7-10]。

本文提出一种基于向量相似性的多维标度定位算法。该算法在构建相关性矩阵方面进行改进，以解决复杂环境对无线信号影响导致的定位精度较低的问题。该研究主要包含两个方面：①以节点采集到的各发射节点的无线信号强度指示构建信号向量，以向量间相似性作为度量节点间距离的度量标准；②使用相关性修正模型对向量间相似度进行修正完善，进而提高定位精度。

1 VSE-MDS算法

本文提出了一种基于向量相似性的多维标度定位方法，引入测量信号参数向量间的相似度作为节点距离的度量标准，在一定程度上打破了传统基于测量信号参数方法的局限性，可以适应复杂环境下的实时定位。

首先，引入测量信号向量相似性指标cosine，它在一定程度上可以衡量两个向量间的相似程度。将两测量信号向量的cosine作为基准，可以有效利用向量特征为节点的相对位置关系提供度量标准。

其次，提出了基于样本熵的相关性修正模型，在使用多维标度算法进行定位前，先利用模型对基准环境下的所有测量信号向量的相似度进行修正，然后利用多维标度算法对修正后的相关性矩阵进行降维，得到目标节点的相对位置坐标。

VSE-MDS(vector sample entropy multidimensional scaling)算法是一种利用测量信号向量间的相似关系来表征目标节点间距离远近关系的多维标度定位算法，并通过样本熵构建相关性修正模型达到进一步优化节点相关性的目的。VES-MDS算法的算法框架见表1。

表1 VSE-MDS算法主要框架

1.1 向量相似性指标

以各目标节点RSSI构建测量信号向量矩阵R，矩阵中的每一行是每一个目标节点的n维RSSI向量，考虑到向量特征，本文引入测量信号向量相似性指标cosine，定义如下：

定义1 信号向量相似性指标cosine。对于向量x，序列y与其的相似度为

(1)

式中：cosine的取值范围为[0,1]。向量间的相似度越高cosine取值越大，当两个向量完全一致时cosine取值为1。

在实验中发现，使用向量相似性指标对向量间相似度进行表征时，由于cosine是针对两向量整体相似性进行表征，存在向量相似性表征不准确的情况。针对这种情况，提出了一种基于样本熵的相关性修正模型。

1.2 相关性修正模型

样本熵(sample entropy，SE)是一种用于比较两个不同时间序列相关性程度的算法[11]。样本熵决定了向量中有多少分向量出现在统计上显著的范围内。当一对向量比另一对向量更相似时，对于所测试的所有条件，它应该具有更低的样本熵。可以看出，样本熵将向量从一个整体拆分为多个小的向量分量并计算各分向量对的cosine指标，通过统计在规定范围内的cosine指标数量来进一步反应向量间的相似程度求得向量样本熵(vector sample entropy，VSE)，进而达到对向量间相关性进行修正优化的目的。

构建相关性修正模型，假设rx=(rx(1),rx(2),…,rx(n))，ry=(ry(1),ry(2),…,ry(n)) 是两个n维向量。输入重构维度m， 考虑到目标节点的分布环境m一般取值为2或3。修正后的向量为：xm(i)=(rx(i),rx(i+1),…,rx(i+m-1)),1≤i≤n-m，ym(i)=(ry(i),ry(i+1),…,ry(i+m-1)),1≤i≤n-m引入相关性指标cosine记为f，对任意i≤n-m有

(2)

于是可以定义

(3)

令向量重构维度变为m+1，于是可以定义

(4)

并且得到

(5)

令1≤x≤n,1≤y≤n， 可以定义各节点向量间的样本熵为

(6)

通过基于样本熵的相关性修正模型对测量信号向量间相似度进行修正，得到各目标节点间测量信号向量样本熵。以各节点间的向量样本熵构成多维标度算法中的相关性矩阵，通过多维标度法对相关性矩阵进行降维得到节点间的相对位置坐标。

1.3 节点位置计算

根据前一节的结果，基于所获取到的各节点之间的相似性关系，我们可以利用多维标度[12]算法来计算待测节点与各发射节点之间的相对位置，最后通过坐标转换的方式，以发射节点的实际物理位置计算出待测节点的位置。

以各节点间的向量样本熵构建矩阵，用V表示，矩阵如下

(7)

使用双重中心化的方法得到内积矩阵，其形式如下

(8)

JN+1为中心矩阵。我们假设距离没有误差，则可以将矩阵转换为

B=XXT

(9)

其中，X=[x1,x2,x3,…,xN]， 用特征值因式分解法可将B分解为

B=VΛVT

(10)

其中， Λ=diag(λ1,λ2,…,λN+1) 是B的特征矩阵，V=[v1,v2,…,vN+1] 是一个标准正交矩阵，其列向量是对应的特征向量。在没有误差的情况下，B的秩为2，B可以转变为以下形式

B=(V2Ω)Λ2(V2Ω)T

(11)

其中， Λ2=diag(λ1,λ2)，V2=[v1,v2]， Ω为正交矩阵。根据式(9)和式(11)我们可以得到主轴解

(12)

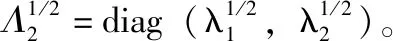
2 仿真实验及分析

为验证VSE-MDS算法的性能，在MATLAB R2016a中进行仿真实验。实验的目标区域为10m*10m的方形区域，在区域内随机部署10个无线传感器发射节点，其中9个为发射节点，1个为待测节点，对待测节点位置进行测量。

本文与传统基于RSSI的多维标度算法进行了对比，验证了算法的改进效果。同时为了验证算法的定位精度，选用Regular Model以及Logarithmic Attenuation Model分别模拟理想传播空间以及非理想传播空间下的无线信号传播方式对算法进行了验证[13]。

本文使用归一化的误差分析模型对算法的性能进行评估

(13)

为考量VSE-MDS算法在不同传播空间下的定位性能，分别在理想和非理想两种不同的传播空间下，分别对基于RSSI的多维标度算法和VSE-MDS算法进行了10次连续测量，连续10次定位结果见表2、表3。

表2 理想传播模型环境下定位10次结果

表3 非理想传播模型环境下定位10次结果

对10次定位结果求平均值，我们可以得出在理想传播型的环境下，基于RSSI-MDS的室内定位方法的平均定位精度为3.04 m，基于VSE-MDS的室内定位方法的平均定位精度为2.28 m。在非理想传播模型的环境下，基于RSSI-MDS的室内定位方法的平均定位精度为3.69 m，基于VSE-MDS的室内定位方法的平均定位精度为2.41 m。从平均定位精度可以看出无论是在理想传播模型的环境下还是在非理想传播模型的环境下，基于VSE-MDS的室内定位方法相较于RSSI-MDS都拥有更加准确的定位精度。

为验证两个算法受环境因素影响的程度，对VSE-MDS算法以及RSSI-MDS算法在不同环境下的10次定位结果进行比对分析，分析结果如图1、图2所示。

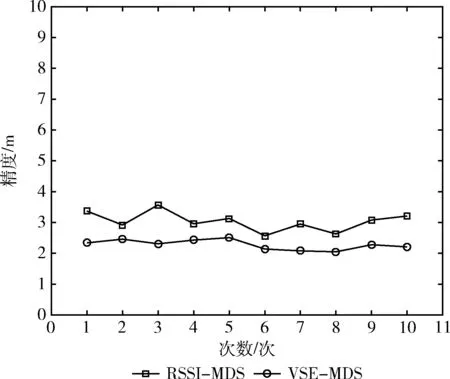
图1 Regular Model环境下定位精度

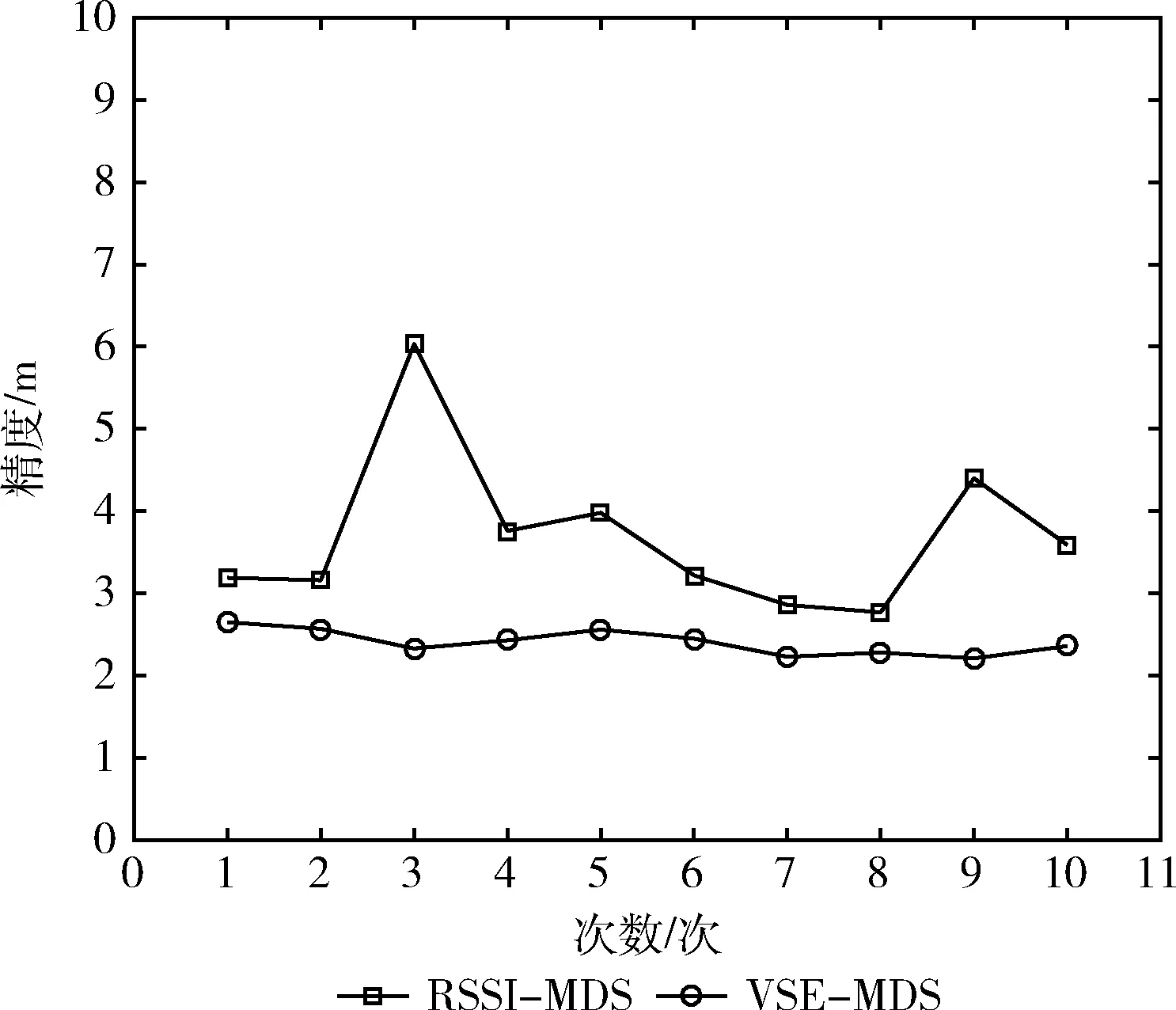
图2 Logarithmic Attenuation Model环境下定位精度

基于VSE-MDS的室内定位方法在多次测量中，定位结果较为一致，同时对比在理想传播模型环境下的定位结果和在非理想传播模型环境下的平均定位精度，基于VSE-MDS的室内定位方法不因环境的变化而产生较大的误差波动。反观基于RSSI-MDS的室内定位方法在多次测量中，定位误差波动较大，同时在环境发生变化后，算法误差产生了较大的变化。因此可以得出基于VSE-MDS的室内定位方法在拥有较高定位精度的前提下，受环境因素影响较小。

为进一步验证算法在实际情况下的实用性，使用4台HUAWEI-WS5200路由器作为AP发射端，一台笔记本电脑作为接收端，实验在8m*10m的环境较为复杂的实验室内进行，在室内各处皆摆放了桌椅。在室内环境中，随机取10个任意位置作为待测点进行实验。室内环境如图3所示。

图3 室内环境布局

在实际随机选取的位置分别连续进行10次测量，并使用VSE-MDS算法对目标节点进行定位，对定位误差进行统计分析的结果如图4所示。

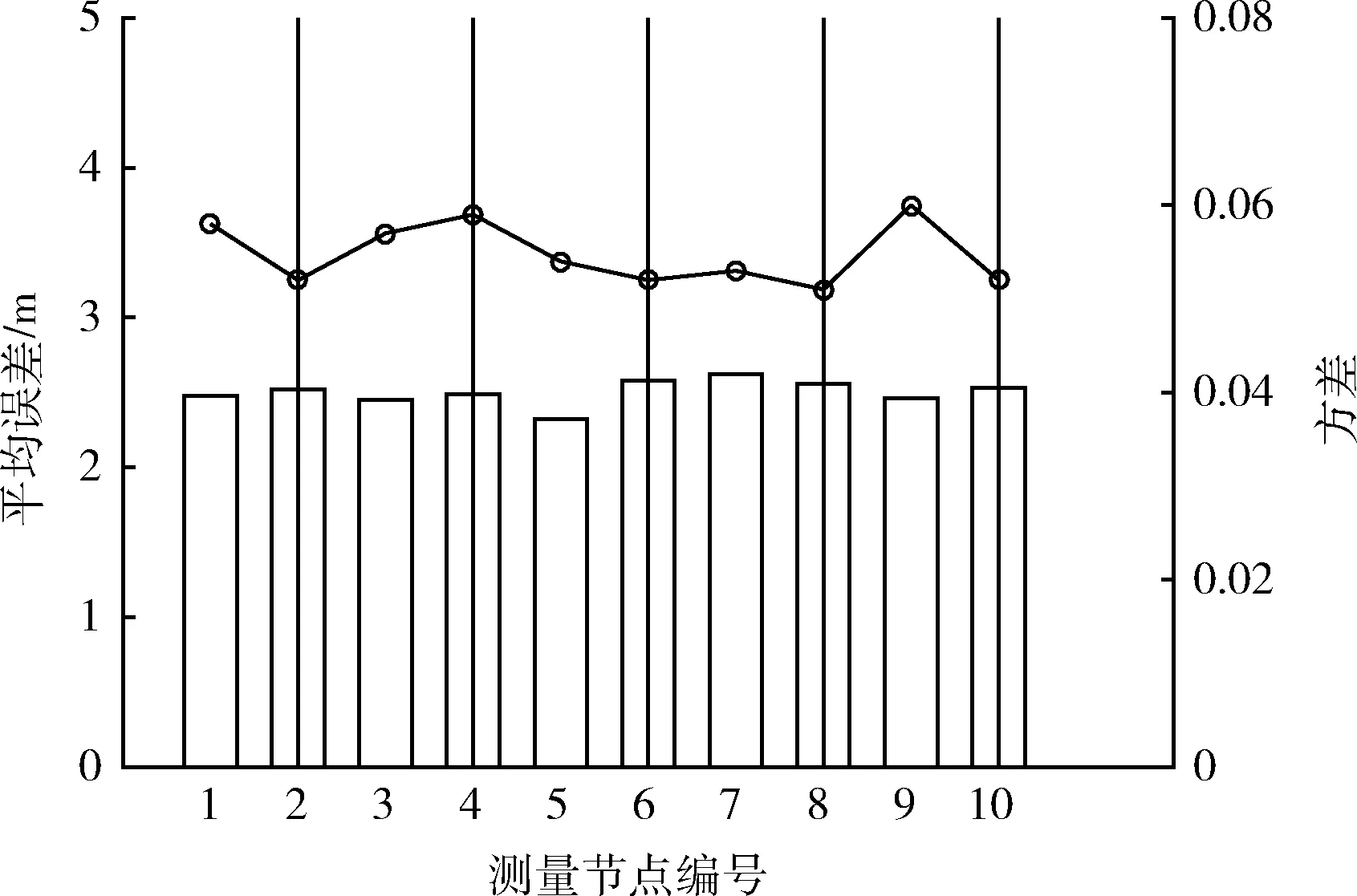
图4 实际测量平均误差及方差

在图4中柱形图表示节点定位的平均误差，折线图表示节点定位误差的方差。根据对各位置定位误差的方差分析可以得出，VSE-MDS算法在同一位置的不同时间段内的定位误差的方差为0.05左右，验证定位误差的波动较小。通过对不同位置的平均定位误差的对比分析可以得出，VSE-MDS算法在不同位置上的定位误差在2.5 m左右，各位置的定位误差较为一致。因此可以得出VSE-MDS算法在实际情况下受复杂环境的影响较小。

3 结束语

提出了一种基于向量相关性的多维标度定位算法VSE-MDS。研究了传统基于RSSI的多维标度的室内定位方法，在传统方法中使用RSSI值构建相异性矩阵会导致定位精度不高、受环境因素影响较大。仿真实验结果表明，基于VSE-MDS的室内定位算法解决了多维标度算法中相关性矩阵优化的问题，同时降低了环境因素对定位结果的影响程度。进一步优化算法定位精度，并将算法引入到移动节点定位中，将是下一步的研究方向。