基于磷虾群算法的并网电动汽车功率优化分配
2021-01-20张丙旭
许 刚,张丙旭
(华北电力大学 电气与电子工程学院,北京 102206)
0 引 言
电动汽车(electric vehicles,EV)作为灵活负荷,在并网时段内,储能电池需要蓄电满足出行需求,但在另一角度,并网的EV集群可以看作一种特殊的分布式储能装置,在配电网负荷高峰时,部分EV在满足离网达到期望电量的前提下,可延缓充电以降低配电网的高峰负荷,甚至可向电网放电进一步削弱配电网负荷高峰。EV集群并网具有巨大平抑负荷波动的潜力,可提高配电网运行可靠性与经济性[1-3]。
文献[4]在微网环境下,考虑EV的移动属性及分时电价机制,采用了改进的遗传算法最小化微网发电成本。文献[5,6]进一步讨论规模化EV并网条件下,以削峰填谷为目标提出了动态电价引导下的EV序充放电策略。文献[7]将EV功率分配分为两个阶段,第一阶段针对单台EV以用户成本最小为目标制定最优功率,第二阶段依据配网的负荷波动指标对第一阶段功率分配结果二次调整。文献[8]建立储能电池迟滞模型,功率增量依据功率计划值与实际值的偏差确定,根据并网EV的状态优先权进行功率分配。文献[9,10]考虑规模化EV并网,采用基于Benders分解的启发式算法,实现并网EV的灵活调度,平衡供需两侧利益。文献[11,12]考虑EV充电需求,采用了改进的粒子群优化算法实现EV的功率分配。
现有研究并未顾及用户的需求差异,且未涉及大规模EV并网的场景。文献[13]虽涉及用户个性化需求,仅浅显考虑了快、慢充两种方式。目前讨论的EV集群并网规模在百辆级,考虑未来EV逐步取代机动车,配电区块内接入EV集群可达千、万辆级。大规模EV集群并网后,在兼顾用户差异需求的前提下,高效的功率分配是亟待解决的问题。
1 需求差异化的EV控制模型
1.1 用户需求差异性
实际场景中,部分用户需求为在最少时段内达到期望电量,表现为EV并网即保持额定功率充电,直到期望电量,此类用户构成不可调度集。其他用户则构成为可调度集,可调度EV在离网可达期望电量的前提下,并网时段内充电功率可被消减甚至储能电池处于放电状态。实际中,供应侧须根据用户差异化需求执行差异化的计价方式且对参与放电的用户提供补偿。
设并网EV全集为S,可调度EV集记为D,不可调度EV集记为G。考虑放电过程会对储能电池性能造成额外损耗,用户对性能损耗具有不同敏感度,将D集进一步细化为子集D1、 D2。 D1中EV并网过程可处于放电状态,D2中EV并网过程不可处于放电状态。依据集合论,上述关系采用式(1)描述
S=D∪G=D1∪D2∪G
D∩G=∅
D=D1∪D2
D1∩D2=∅
(1)
1.2 EV储能电池控制模型
设Rl∶{Tarr,l,Tdep,l,Co,l,Ce,l,El,Pc,l,ηc,l,Pd,l,ηd,l} 为车辆l,l∈S的参数集。Tarr,l,Tdep,l,El分别为l的并网时间、离网时间及储能电池容量;Co,l,Ce,l分别为l的并网、离网时荷电状态(state of charge,SOC),SOC为储能电池电量与El的比值。Pc,l,ηc,l,Pd,l,ηd,l分别为额定充电功率、充电效率、额定放电功率、放电效率。
设车辆l并网功率初值为Pc,l。Pc,l,t,Pd,l,t分别为t时实际充电功率、实际放电功率。设Δt为优化步长,储能电池充放电控制模型如下:
(1)∀l∈D1, 当t∈[Tarr,l,Tdep,l] 时,车辆l的荷电状态SOC由式(2)计算

(2)
[kc]∈rc表示处于充电状态的时段数, [kd]∈rd表示处于放电状态的时段数。Pc,l,t,Pd,l,t,Cl,t分别为车辆l在t时的实际充电功率、放电功率、SOC。式(2)不等式表示充放电功率约束,表示子集D1中EV可充电也可放电。
(2)∀l∈D2, 当t∈[Tarr,l,Tdep,l] 时,SOC由式(3)计算
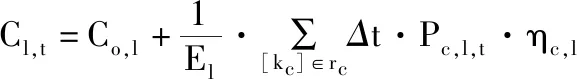
(3)
式(3)不等式约束D2集中EV不可处于放电状态。
(3)∀l∈G, 当Cl,t∈[Co,l,Ce,l] 时,SOC由式(4)计算。
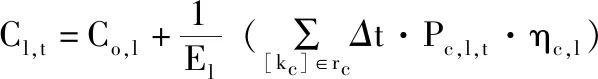
(4)
式(4)约束G集中EV在SOC未达到期望值前,始终保持额定充电功率充电。
为简化运算,本文假设所有车辆的El,Pc,l,ηc,l,Pd,l,ηd,l均取相同值,分别为80 kWh、10 kW/h、0.9、10 kW/h、0.9。
1.3 D集EV调度优先权
定义指标γl,t为车辆l在t时的调度优先权。不可调度集G中EV功率恒定。因此,γl,t指标的计算只针对D集。建立用户诚信度、削减率、反向供电能力3个指标综合评估D集车辆的调度优先权。
(1)信用度Il衡量用户按照约定Tdep,l时刻离网的可信度

(5)
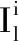
(2)消减率cl,t衡量EV在 [Tarr,l,t] 时段内功率消减程度
(6)
车辆l在并网时段内功率越趋近于额定充电功率,消减率越小。
(3)放电能力dl,t衡量EV在当前时段内进行放电的优先程度
(7)
当前时段距Tdep,l越长,且Cl,t越接近期望值Ce,l, 放电能力越大。
l在t时的调度优先权γl,t为γl,t=(Il+dl,t)/cl,t。
2 优化目标及约束条件
为避免并网EV集群集中式控制面临的“维度灾难”[14]。采用分布式控制方式,电动汽车聚合商(electric vehicles aggregators,EVA)作为EV与配网的中介,可以对配电区块的EV负荷进行聚合,不同的EVA对所辖EV集群实现分布式控制。以EVA总功率波动最小为目标,建立目标函数Fobj
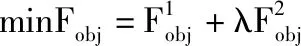
(8)
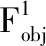
(1)EV离网时需达到期望电量,电量在储能容量范围内,且放电时储能电量不低于限值Cthr
(9)
其中,Cdep,l为车辆l离网时的SOC;Cthr为放电阈值,本文统一设置为0.5。当车辆l处于放电状态时,Cl,t不低于0.5。
(2)EV在同一时段内不可同时处于充电状态和放电状态
Pc,l,t·Pd,l,t=0,∀l,t
(10)
(3)EV并网时长需满足最短并网时长约束
(11)
3 EV并网功率分配策略
3.1 磷虾群(KH)算法
KH算法是由Gandomi和Alavi提出的新型智能算法。文献[15]已验证KH算法较著名的遗传算法(GA)、差分进化(DE)、蚁群优化(ACO)、粒子群优化(PSO)和加速粒子群优化(APSO)等算法更具优势。
磷虾个体的移动由诱导Ni、 觅食Fi、 扩散Di这3类活动主导。磷虾移动方向的拉格朗日模型为
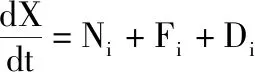
(12)
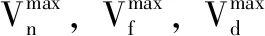
磷虾个体的位置更新公式如下
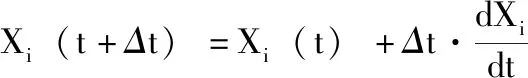
(13)
其中,κ为位置更新步长Δt的控制因子;nv为变量Xi的维度;Ubj,Lbj分别为变量Xi第j维元素取值的上下限。
KH算法具有明显优势,但在全局最优及计算收敛速度仍具有局限性。式(12)中的αi在文献[15]中是由邻域群体诱导及最优个体诱导共同决定。文献[16]及文献[17]分别引入紧邻套索算子及动态压力控制算子,克服了群体诱导及最优个体诱导可能导致的算法陷入局部最优的局限性,提高了KH算法的全局搜索能力。在此基础上,针对并网EV的功率分配,采用动态自适应权重策略及余弦递减步长演进策略对算法进一步改进。
(1)动态自适应权重策略
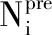
(14)
Ki,r-1,Ki,r分别为磷虾i在第r-1次迭代和第r次迭代的适应度。
(2)余弦递减步长演进策略
式(13)中κ经验取值范围为[0,2][15]。κ的取值对平衡算法的全局开采与局部勘探能力起决定作用。功率分配采用κ逐渐减小的动态调整策略,迭代前期取较大κ值增加全局开采能力,在后期趋近最优值时,缩小κ值增强算法局部勘探能力。κ取值采用式(15)的余弦递减策略
κr=((κmax-κmin)/2)·cos(π·r/rmax)+(κmax+κmin)/2
(15)
当κmin=0,κmax=2时,3类不同策略下κ取值随迭代次数的变化如图1所示。采用线性递减策略,κ值下降速率恒定,局部勘探能力差,算法收敛效率低。采用指数递减策略或余弦递减策略,在一定程度上平衡了全局开采与局部勘探能力,迭代前期,指数递减策略κ值下降速率快,全局开采能力弱于余弦递减策略。
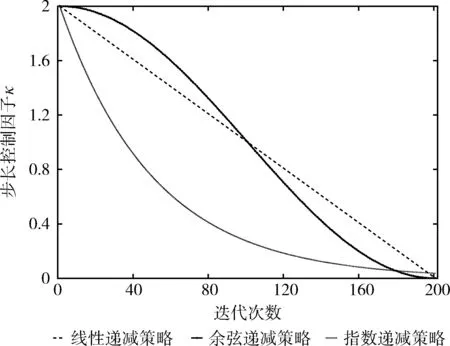
图1 3种策略下的κ值变化
3.2 基于改进KH算法的EV集群功率分配
第一阶段优化:对EVA进行功率分配。此时,磷虾位置对应表示Ne个EVA在NT时段的功率;迭代过程磷虾个体的移动(对应功率变化)采用式(12)~式(15)计算,式(13)中上下限Ubj,Lbj在式(1)~式(4)的约束下求解。
算法1:EVA功率分配算法
输入:NT时段内功率Pb,t;Ubj,Lbj; 最大迭代次数rmax
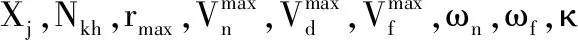
for i=1:rmax
计算每个磷虾个体的目标函数值Fobj
forj=1∶Nkh
依据式 (12) ~式 (15) 计算Ni,Fi,Di, 首次迭代时ωn,ωf,κ均取初始值且λ1=0; 磷虾个体位置通过式 (13) 更新
end for
更新磷虾种群;计算新种群磷虾个体目标函数值Fobj
依据式 (14) 更新ωn,ωf
依据式 (15) 更新κ
end
输出: 每个EVA在NT时段内的功率
第二阶段优化:每个EVA对所辖EV进行功率分配。分配过程需要考虑所辖EV的所属集及调度优先权,充分保证用户差异性需求。EVA之间相互独立,多个EVA同时采用改进KH算法并行优化,优化过程满足约束式(1)~式(4),式(9)~式(11)。
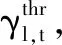
(16)
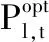
设磷虾个体j在t时位置Xj,t中元素xj,t,y对应车辆l在t时的功率,计算γl,t, 元素xj,t,y的更新步长控制因子采用式(17)计算。因此第二阶段优化中,式(13)中Δt取值不仅具有时变性,且因车辆不同而取值不同,第二阶段优化Δt转换为与Xi等维度的序列,式(13)由式(18)、式(19)代替
(17)
(18)
(19)
其中, [Δt]s表示序列Δt中第s个元素;κl,t为[Δt]s对应的车辆l在当前时段的步长控制因子, []·[]表示对应元素相乘。
算法2: EV功率分配并行算法
输入: 算法1求解的NT时段内EVA的优化功率, 基础功率Pb,t,rmax
EV的所属集标签及车辆参数{Tarr,l,Tdep,l,Co,l,Ce,l,El,Pc,l,ηc,l,Pd,l,ηd,l}
par for k=1∶Ne
for i=1∶rmax
forj=1∶Nkh
求解每辆EV的γl,t; 通过式(17)计算κl,t
依据式 (12)、 式 (14) ~式 (17) 计算Ni,Fi,Di
依据式 (18)、 式 (19) 更新磷虾个体位置
end for
检测任意磷虾个体Xj满足约束式 (9)、 式 (10)
依据式 (14) 更新ωn,ωf
依据式 (15) 更新κ
end for
end par for
输出: 每个EV在NT时段内的功率。
算法1(第一阶段优化)输出每个EVA在NT时段内的功率,算法2(第二阶段优化)每个EVA独立对EV进行功率优化。整体迭代可达到EVA功率与EV功率分配协同最优。设两个优化阶段的整体迭代次数最大为rz, 随着迭代次数增加,两个阶段优化目标函数快速减小,为进一步增强算法全局搜索能力,目标函数中Fobj的惩罚因子λ按式(20)更新
(20)
λr为第r次迭代时的惩罚因子。两阶段交互协同优化步骤如下:
(1)输入每个EVA的EV集群接入数量;输入rz,NT,Ne;
(2)首次迭代(r=1)时,因EV的实际功率未知,置λ1=0,r≠1时,λr采用式(20)计算;
(3)执行算法1及算法2。r=rz时,跳转步骤(4);r≠rz时,令r=r+1, 跳转步骤(2);
(4)输出EVA功率及EV并网功率。
4 算例分析
4.1 实验数据
EV集群规模为5300辆。4个EVA参与,每个EVA最大可接入EV数量分别为600,1100,1600,2000。采用蒙特卡洛模拟的方法生成车辆Tarr,l,Tdep,l,Co,l。 设并网EV所属D1,D2,G集比例为5∶3∶2。在MATLAB 2016a环境下编程仿真,计算机的配置为Intel(R) Core i5-7200U @2.50 GHz,双核,8 G内存。
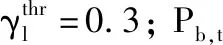
4.2 结果分析
采用蒙特卡洛模拟得到EVA实际接入的EV数量见表1。
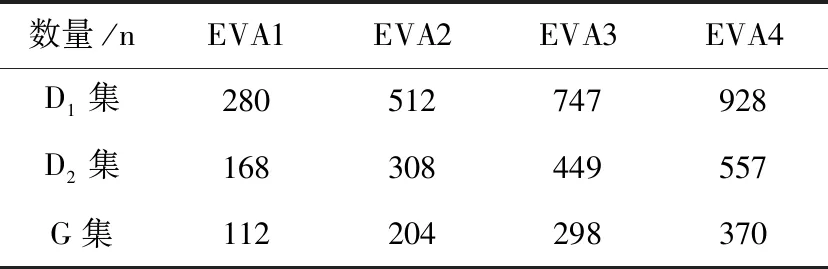
表1 EVA所辖3类EV并网数量
为确定rmax,rz最优值,对算法测试,得到目标函数随迭代次数变化如图2所示。
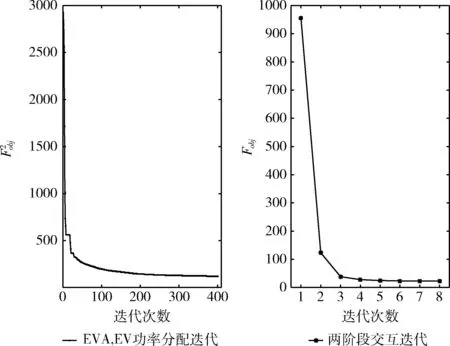
图2 目标函数随迭代次数的变化
如图2可知,采用改进KH算法,EVA功率分配和EV功率分配迭代次数取值rmax=200。 取两阶段交互迭代次数取值rz=6。
设任一EV并网即以额定功率充电为EV集群并网的无序模式。采用本文所提功率优化分配策略确定EV并网功率,为EV集群并网的有序模式。rmax、rz分别取值为200、6时,无序充电模式与本文采用改进KH算法得到的有序模式的结果对比如图3所示。
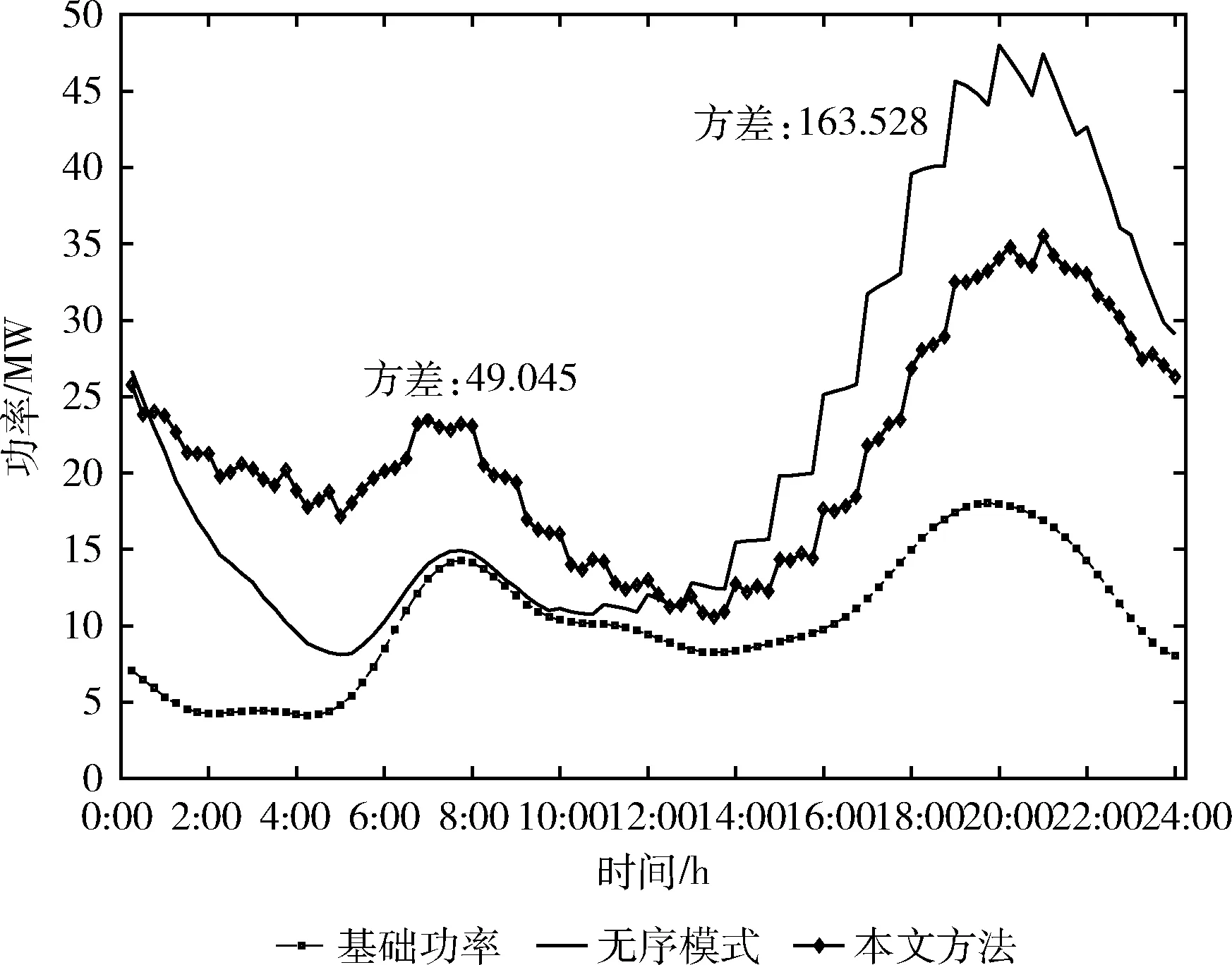
图3 无序模式与有序模式结果对比
无序模式下,总功率在96时段内的方差为163.528。采用改进KH算法得到的有序模式下,总功率方差为49.045,功率波动减小70%,有序模式具有明显的削峰填谷的效果。
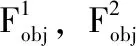
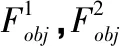
表2 6次迭代下及EVA功率变化
以EVA4为例,跟踪其中3辆EV在并网时段内的功率变化及储能电池电量变化,如图4所示。
如图4所示,L1(12∶00-24∶00,0∶00-9∶00并网)、L2(4∶00-15∶00并网)、L3(13∶15-24∶00,0∶00-8∶00并网)分别属于D2,D1,G集。阶梯图表示对应EV并网功率的变化,相同标记的折线表示对应EV荷电状态SOC变化。L3属于G集,为不可调度EV,虽然并网时段较长但仍以额定功率进行充电,至20:30储能电池蓄满电量,在其余时段,因L3不可调度,L3虽与充电站处于物理连接状态,实际处于中断状态。L2在并网时段内,处于放电状态的时段数为10,最大放电功率在第28时段为9.347 kW,最小放电功率在第56时段为0.781 kW。L1在部分时段内进行了充电功率削减,但并网时段内储能电池均未出现放电状态,在第33时段,L1调度优先权为0.357,小于L2调度优先权为0.813,L2功率由上一时段的充电9.941 kW消减为放电4.308 kW,L1调度优先权较小,当前时段已临近离网时刻,为保证用户用电需求,充电功率较上一时段有所增加。3辆EV离网时SOC分别为0.997,0.9684,1。功率优化分配策略保证用户差异性需求的同时满足了用户的用电需求。
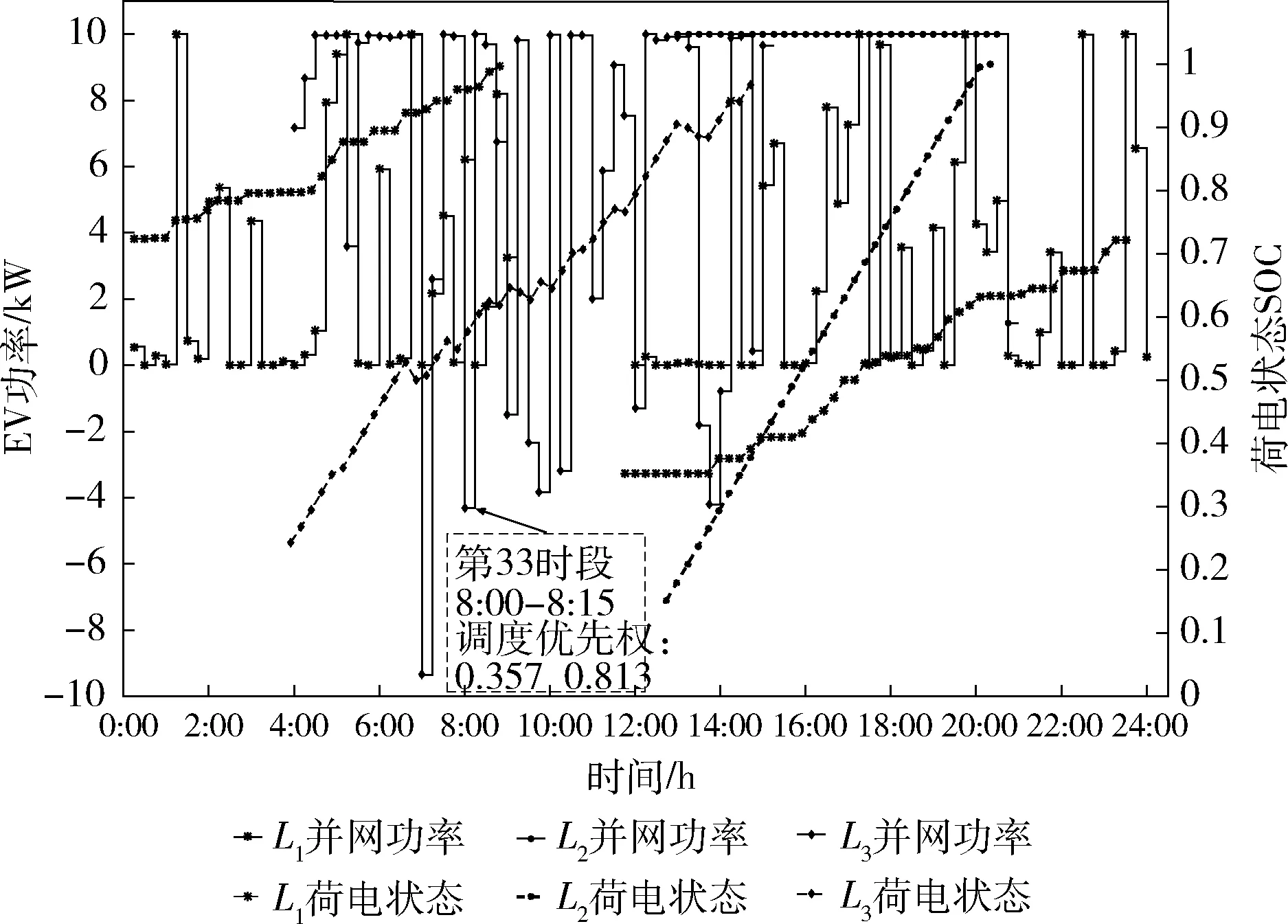
图4 EVA4中3辆EV充电功率及SOC变化
为验证改进算法的性能,以标准的KH算法[15]、引入紧邻套索算子及动态压力控制算子的改进KH算法[16,17]与本文改进算法进行对比。优化算法的参数设置保持一致,第二阶段优化均采用并行计算,得到最优迭代次数、目标函数值及求解时间见表3。

表3 3种KH算法下的求解结果
标准的KH算法求解精度低于文献[16,17]改进KH算法和本文方法,且标准的KH算法求解所需时间分别为改进KH算法和本文方法的2倍、3倍。文献[16,17]改进的KH算法与本文算法具有相似的求解精度,但本文提出的KH改进算法可在更少的迭代次数下收敛,求解效率提高26.9%。
需要指出,优化策略中第二阶段EV功率优化采用并行优化,因此求解效率主要取决于实际并网EV数量最大的EVA4,即EVA1-EVA3可同时扩展到与EVA4相同的EV数量,而不会增加算法的求解时间。此外,本次模拟的计算机环境仅为双核四线程,若提高计算机性能,可进一步降低求解时间。
5 结束语
针对大规模EV并网功率分配,提出基于KH算法的EV集群功率高效分配策略。本文主要完成的工作总结如下:
(1)考虑用户需求差异性,将并网EV细分为3个子集,分别建立需求差异化的EV储能电池控制模型。
(2)设计了两阶段分散式功率分配策略。针对性提出动态自适应权重策略及余弦递减步长演进策略改进KH算法,减少算法中的无效迭代,提高了算法的收敛效率和求解精度。
(3)模拟5300辆并网EV的功率分配,验证了所提策略的高效性,保证用户需求的同时可兼顾用户的差异性需求。
后续研究中,将考虑实际场景中的EV随机并网与离网特征,增强算法的鲁棒性。另一方面将继续优化算法,降低求解时间,实现大规模EV并网实时调度。
