基于双法线跟踪的形状中轴并行提取算法

朱厚盛，鲍宪帅，朱春元，陈明胜

(大连海事大学 信息科学技术学院，辽宁 大连 116026)

0 引 言

作为一种形状描述的工具, 中轴概念[1]是由Blum于1967年首次提出并应用于图像领域, 发展并推广应用于高维情形。中轴可以看成是平面域内边界所有最大内切圆的圆心集合[2],如图1所示。由于中轴的良好特性, 因此被广泛应用于各个领域中,例如形状表示及变换[3]、医学影像[4]、网络规划[5]、形状分割[6]等。

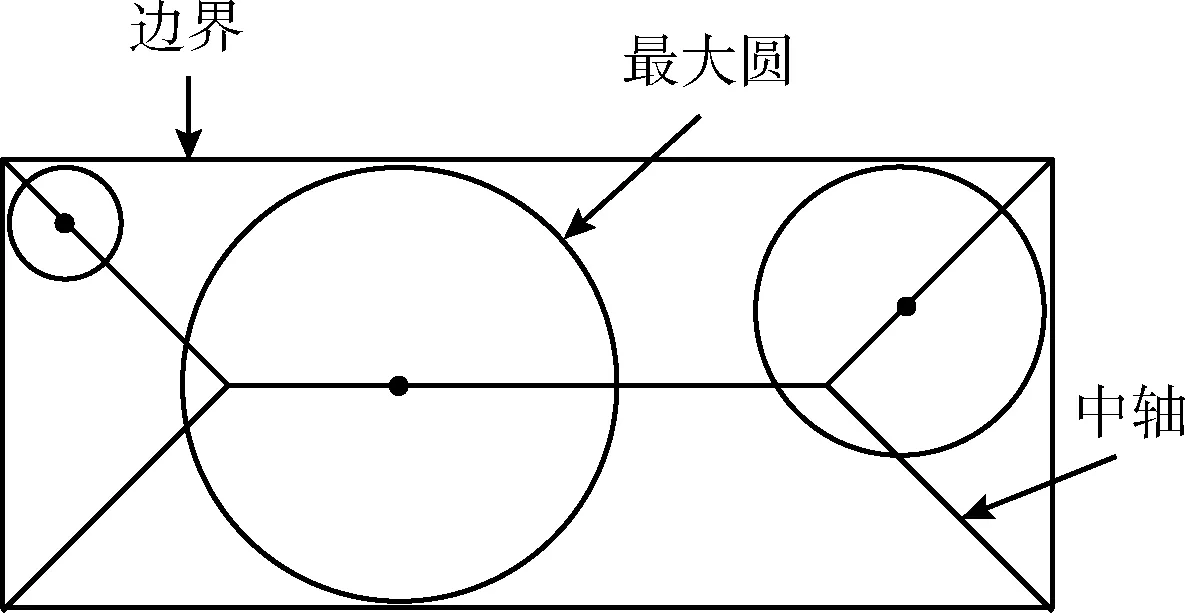
图1 最大圆模型

目前计算形状中轴的方法普遍存在两个缺点,即高时间成本或低中轴质量。首先,目前大多数方法都使用并行度不高的CPU作为主处理器,生成中轴的时间成本较高, 因而可以使用GPU的并行计算来快速计算出形状中轴。其次, 目前中轴的计算方法离散程度较高, 导致求解出的中轴精度不足。

考虑以上因素, 本文提出了一种基于双法线跟踪的形状中轴并行提取算法, 该算法可以高效得到形状的高质量中轴。该算法步骤如下：①将形状的包围盒分割成若干的网格单元, 以便于接下来的并行化处理。②根据精度要求, 将形状的边界离散成由若干采样点连接成的多边形。③估计边界点和边界边的法线方向。④以迭代方式计算每个采样点的相应中轴点。最后,通过样本点的拓扑连通性连接中轴点生成中轴。由于所有边界点的法线方向都是高精度的,而使用这些法线来生成的中轴点是遵循中轴的定义的，因此所生成的中轴也是高质量的。

1 相关工作

按照对对象处理方式的不同, 可以将目前已存在的中轴提取算法划大致分为三大类：中轴变换算法、细化算法和形状分解算法。

中轴变换算法是Blum在1973年所提出的。中轴变换算法的主要原理是利用中轴的最大圆盘的定义, 即物体的中轴是物体内部最大圆盘的圆心组成的点集, 由此可知中轴点与形状边界有两个或两个以上的切点。该算法主要用于处理多边形模型或参数曲线曲面模型等连续模型对象, 通过利用严格的数学方法求解, 得到的结果精度较高, 计算过程较为复杂, 在处理复杂模型时稳定性不高, 所以该方法常用于几何建模和物体重建。Zhu等[7]提出了一种在平面域生成自由曲线边界形状中轴的方法。该方法在边界曲线上采集足够多的样本点,利用这些样本点计算Voronoi图生成初始中轴；然后基于单向Hausdorff 距离对初始中轴进行裁剪, 得到平面域的最终中轴。Li[8]针对中轴变换的不稳定性及冗余性提出了基于二次误差最小化的中轴变换简化算法(Q-MAT)。在此算法中将中轴变换的简化转换为中轴网格合并简化的问题, 并对二次误差度量框架进行了改进, 能够有效的移除中轴变换中不重要的分支, 得到一个简单紧凑且较为准确的中轴变换。而本文则同样是利用网格来求取中轴, 主要是利用中轴定义跟踪法线计算中轴, 并且加入了GPU并行计算, 从而大幅度提高了算法上的高效性。

细化算法一般是以像素为对象进行操作的。在数字图像处理中, 我们通常认为当前像素点(物体图像上的点)为黑色, 而背景像素点为白色。细化算法的主要原理就是利用迭代算法对图像中的边缘像素点进行剥离, 在保证拓扑性和连续性不变的情况下得到只有一个像素宽度的原图像的简化图形的表示。此类算法应用于离散化对象, 如像素形状、体素形状、点云形状等。Brunner等[9]提出了一种获取形状中轴的方法, 该方法是从模型边界开始删除无用的像素点, 并向内部进行删除操作, 直到没有要删除的点为止, 在这个过程中需要一些额外的因素来保持模型的拓扑特征。Hu等[10]在完全并行细化算法的基础上提出了一种面向多孔介质的孔隙网络中轴提取方法, 该方法计算较为简单, 并且可以较好保持模型的全局特征, 但是该方法的重构过程较为复杂。Zhu等[11,12]提出了一种基于边界扩张法的形状中轴生成算法。由于离散方法通常是在离散对象上进行的,其精度低于中轴变换算法。

形状分解算法的主要原理是先将原平面图形进行分解, 再对分解后的小图形求取中轴, 最后将得到的中轴连接起来合成原平面图形的中轴。Wang等[13]提出了一种新的增量聚类算法, 此方法应用于书法字的中轴提取。首先通过K-均值聚类算法对书法字图像进行分割,利用新的增量聚类算法对部分中轴进行提取,最后通过拓扑连接形成完整的书法字中轴。Zhu等[14]提出了一种利用扩张法将形状平均划分为不同部分并生成等分子中轴的方法, 考虑了相邻部件之间的影响, 并结合这些子中轴点生成最终中轴。并行化可以提高算法的效率, 但由于被除数的限制, 并行度不高。

2 方法简介

本文为了获得形状中轴, 首先将形状的包围盒分割成为若干的网格单元, 然后将形状的边界离散为若干样本点连接成的多边形。为了并行计算中轴点, 分别估计样本点和边界边的内法线方向(后文中所提及的法线皆为内法线)。如图2所示, 为了计算样本点Pi的中轴点 (i=1,2,…,5), 需计算它们的内切圆。根据中轴的定义可知, 内切圆的圆心即是样本点Pi的中轴点Mi。这里,内切圆上的另一个边界点Qi被称为样本点Pi的对偶边界点,对偶边界点Qi所在的边界边被称为样本点Pi的对偶边界边,样本点Pi的内切圆半径ri被称为样本点的中轴半径。对于任意一个样本点P,为了计算其内切圆, 需要首先搜索所有的边界边, 以便确定样本点的对偶边界边。样本点P的内切圆可能和边界有多个切点, 从而样本点可以具有多于一个的对偶边界边, 但它们中的任何一个均足以计算出样本点P的内切圆。计算出对偶边界边后, 通过利用样本点P及其对偶边界边的信息求解方程(详情见5.3节), 可以计算出样本点P的中轴点M和中轴半径r。最后, 根据样本点的拓扑关系, 连接所有样本点的中轴点, 即可生成形状中轴。

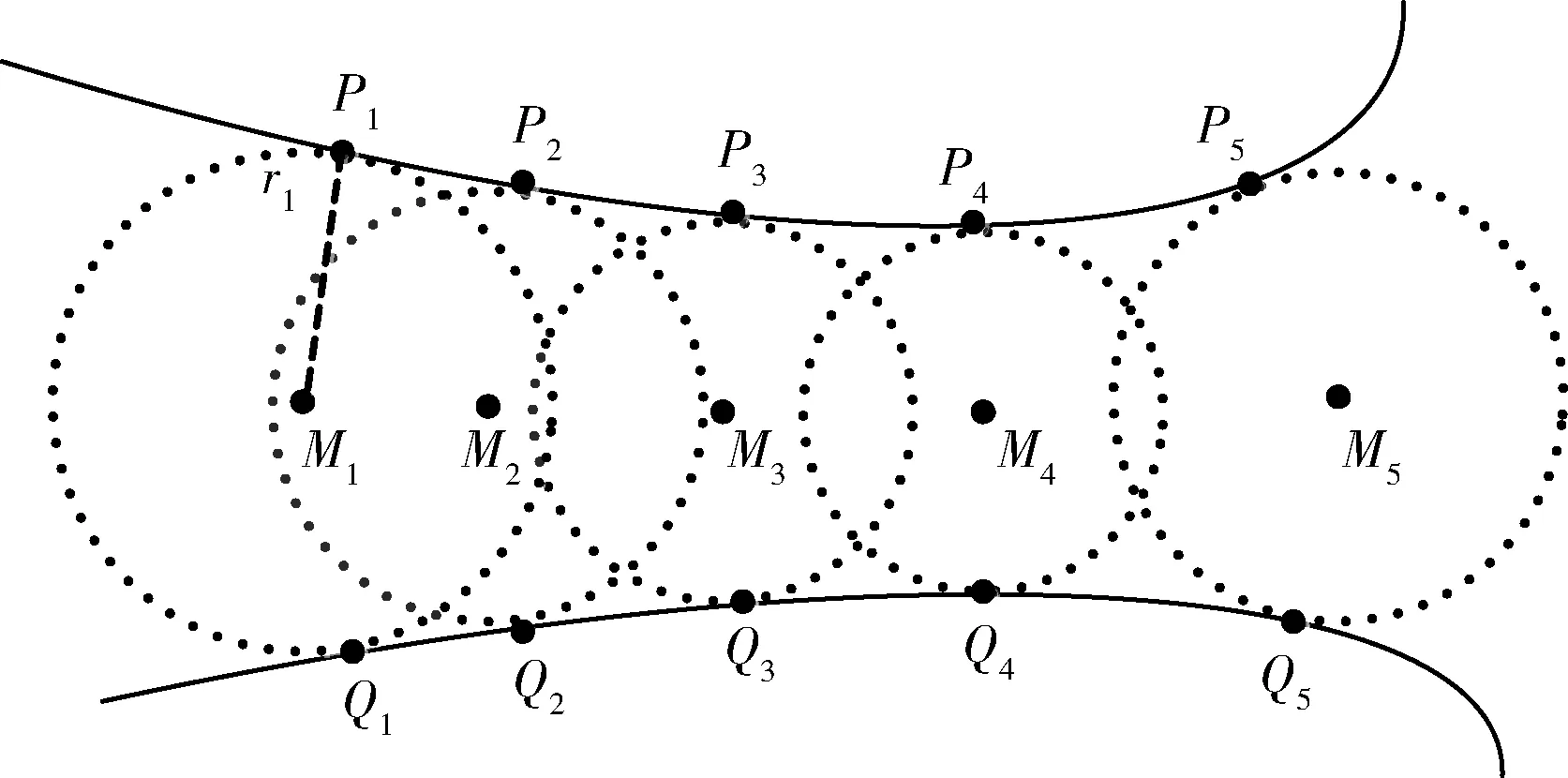
图2 样本点P1-P5的中轴点M1-M5和对偶边界点Q1-Q5

本算法主要分成5个部分, 如图3所示。

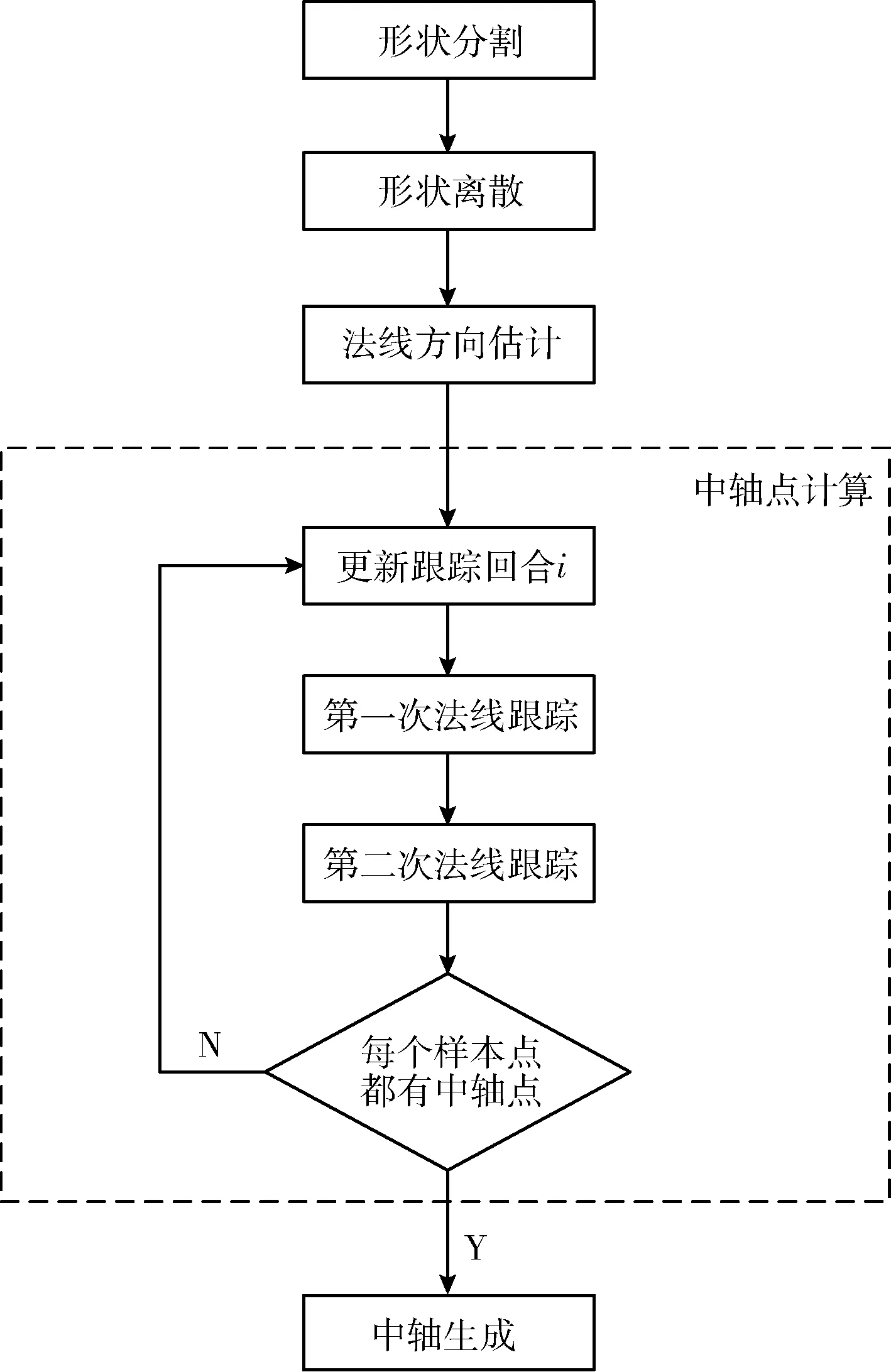
图3 方法概述

(1)形状分割：将形状的包围盒划分成若干的网格单元, 每个网格单元的边长为单元尺寸, 长度为gl。

(2)形状离散：将形状的边界离散为若干样本点连接成的多边形。

(3)法线方向估计：估计边界上所有样本点及边界边的法线方向。

(4)中轴点计算：将所有的样本点先放入待计算的样本点集合中。在每一个追踪回合i, 按照步骤(5)和步骤(6)计算中轴半径在(i×gl,(i+1)×gl)的样本点的中轴点, 并将已经计算出中轴点的样本点从集合中删除。每个回合之后, 待计算的样本点集合中的样本点数量都会减少, 直到计算出所有样本点的中轴点, 则中轴点计算过程结束。这里, 范围(i×gl,(i+1)×gl)称作回合i的当前范围。

(5)样本点的第一次法线跟踪：对于每个未计算出中轴点的样本点, 跟踪它在当前范围的法线段所在的网格单元, 将该样本点存储到网格中, 记录为该网格的候选样本点。每个样本点的跟踪需分配一个GPU线程。

(6)边界边的第二次法线跟踪：对于每个边界边, 跟踪它在当前范围的法线段簇所在的网格单元。对于网格中每对候选样本点和边界边, 计算出样本点的中轴点。每个边界边的跟踪需分配一个GPU线程。

(7)中轴生成：通过样本点的拓扑连接性, 将每个样本点对应中轴点连接起来形成中轴段, 进而形成形状的中轴线。

3 前期工作

3.1 形状分割

为了接下来的并行计算, 形状所在的包围盒需要进行分割成若干网格。通过切割x轴和y轴, 形状的包围盒被分割成多个正方形的网格单元, 其中网格单元的边长被称作单位长度gl。网格单元的数量太少会影响并行度, 太多则会增加跟踪的迭代次数, 因而可根据图形大小适当分割。如图4所示, 模型M在x轴和y轴上分别被分割6块、7块, 最终被分成42个网格单元。

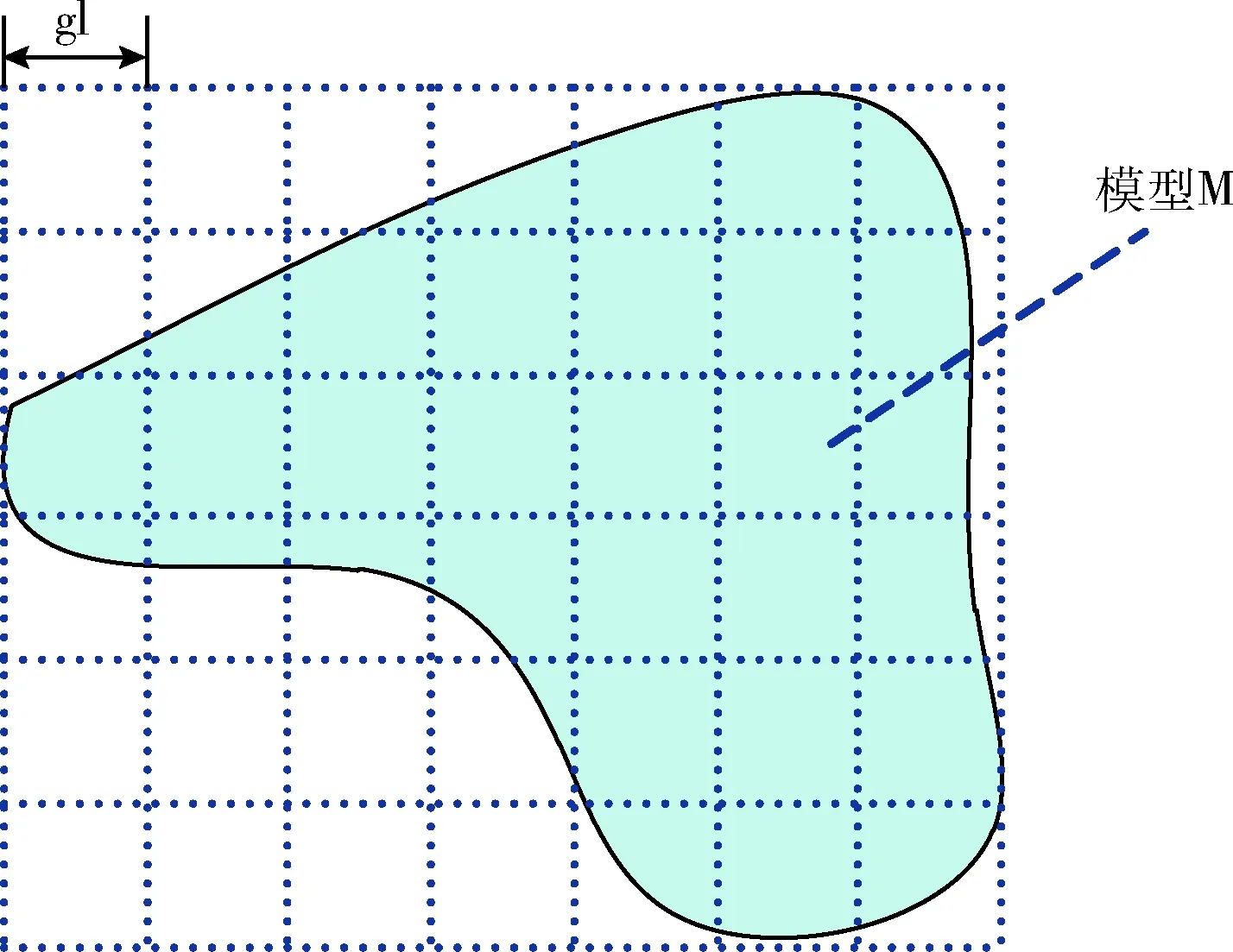
图4 形状分割

将形状分割后, 在后续的算法中, 可以将样本点的搜索范围限制于相应的网格单元中, 通过这种方法可以减少搜索范围, 加快算法速度。同时,也便于引入GPU线程, 对不同网格的中轴点计算进行并行化处理。

3.2 形状离散

在将形状的包围盒分割完成后, 需要对形状的边界进行离散。首先将形状的边界提取出来, 而后将边界离散为若干等距离的样本点, 并将样本点相连接在一起。经过离散操作后, 形状就会离散成由这些样本点连接而成的多边形。可以通过确定离散出的样本点的数量来控制该方法的准确性和复杂性。样本点数量越多, 最终得出的中轴越准确, 但相应的复杂性也会略有提高。

3.3 法向估计

根据中轴的定义, 样本点的内切圆与边界至少有两个切点。其中一个为样本点本身, 另一个在某条边界边上。内切圆的圆心为样本点的中轴点, 中轴点就在两个切点的法线上。为了计算每个样本点的中轴点, 需要获得样本点和各个边界边的法向。

样本点的法向是由和其相邻的边界边的法向决定的。如图5所示, 样本点P点的相邻边界边是AP与BP, 它们的法向NAP与NBP是分别垂直于边界边AP、BP的, 而P的法向NP则是NAP和NBP的中分线。

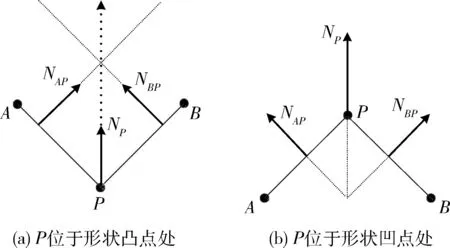
图5 样本点P的法向估计

边界边上的点的法向是由边界边端点的法向与该点在边界边的位置所共同决定的。如图6所示,Q是边界边AB上的点,NA与NB分别是样本点A、B的法向,设AQ∶QB=x∶y, 其中x+y=1, 则Q的坐标为：Q=xB+yA,Q的法向为

NQ=x×NB+y×NA

(1)

根据等式(1)可知, 当Q位于点A或B时,NQ等于NA或NB。当Q′为点Q附近一点时,Q′坐标为：Q′=(x+εx)B+(y+εy)A, 其中εx与εy趋近于0, 此时Q′的法向为

NQ′=(x+εx)×NB+(y+εy)×NA

(2)

比较等式(1)和等式(2)可知,Q′法向是无限接近于Q点法向的, 所以可知边界边上的点的法线方向是连续的。边界边上的点的法线的集合可以看成是该边界边的法线簇。图6中,AS1和BS2长度为i×gl,S1E1和S2E2长度为gl, 那么线段E1S1和E2S2可以看成是点A和B在当前范围的法线段, 而E1S1S2E2可以看成是AB在当前范围的法线段簇。需要说明的是,在实际情况中,边界边AB的长度是较小的, 网格单元gl长度是较大的。文中这样画图是为了方便说明、理解。

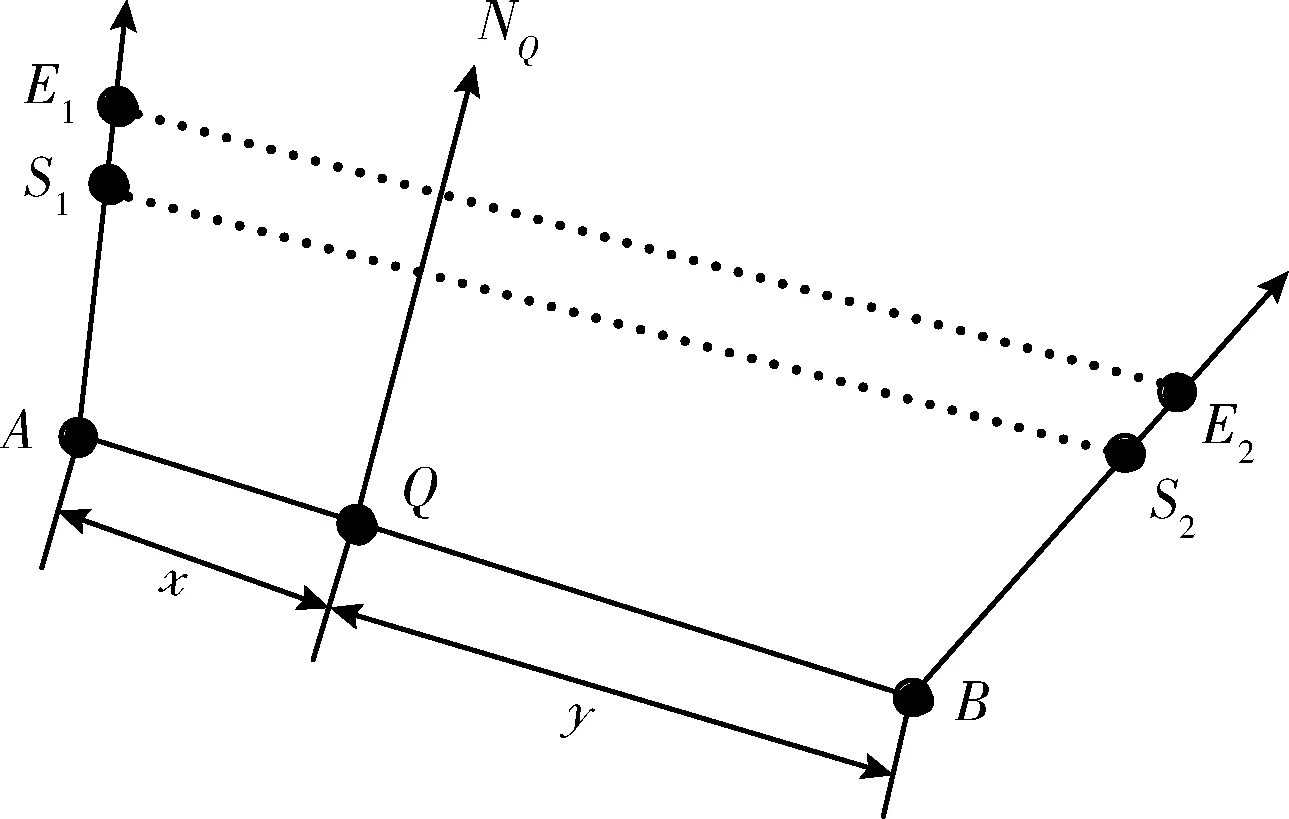
图6 边界边上的点Q的法向估计

4 算法阐述

算法的主要步骤可以分为5个小步骤, 如图7所示。

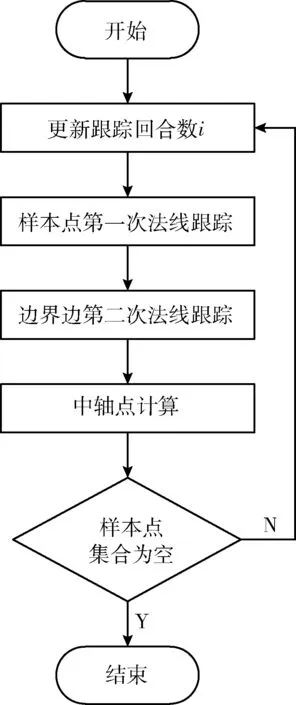
图7 算法流程

(1)更新跟踪的回合数i：在此步骤中对控制迭代的变量i进行加一操作。

(2)第一次法线跟踪：跟踪每一个未计算出中轴点的样本点, 将样本点的中轴点确定在某些网格单元中, 将样本点记录到网格单元中, 详细步骤在5.1中具体描述。

(3)第二次法线跟踪：跟踪每一个边界边在当前范围的法线段簇所在的网格单元, 在网格单元中记录相应的边界边, 详细步骤在5.2中具体描述。

(4)中轴点计算：在两次跟踪之后, 网格单元中会包含一些样本点和边界边, 根据对应关系可计算出中轴点在该网格单元中的样本点的中轴点, 详细计算步骤在5.3中具体描述。

(5)判断迭代结束条件：将已经计算出中轴点的样本点从样本点集合中删除, 如此时样本点集合为空, 则算法迭代完成；如集合不为空, 则算法继续。

5 双法线跟踪算法

根据中轴定义, 本文利用切点法向提出了一种并行双法线跟踪算法。通过该算法,可以迭代地计算出每个样本点的中轴点, 进而得到形状中轴。

双法线跟踪算法是一个迭代过程,涉及多回合跟踪,其中第一次称为第0回合。在第i回合跟踪中,中轴半径在(i×gl,(i+1)×gl)范围内,即在当前范围内的样本点将得到它们的中轴点。在每回合迭代之后,因为已经能够计算出一些样本点对应的中轴点,所以这些样本点不需要参加下一回合的计算,因而待计算的样本点数量变小。经过多回合迭代之后,所有的样本点都得到了它们的中轴点,算法结束。在每一回合计算中,需要两次法线跟踪,即样本点的第一次法线跟踪和边界边的第二次法线跟踪。

5.1 样本点的第一法线跟踪

样本点的第一法线跟踪是通过迭代地跟踪其法向射线来计算它的中轴点。根据中轴定义可知，每个样本点P的中轴点M必定在其法向射线NP上。如图8所示，在第i回合中，设样本点P的中轴半径在当前范围内，则其中轴点M必定在当前范围的法线段SE上。该法线段起始于点S，其中PS是i×gl，并在点E处结束，PE为(i+1)×gl。

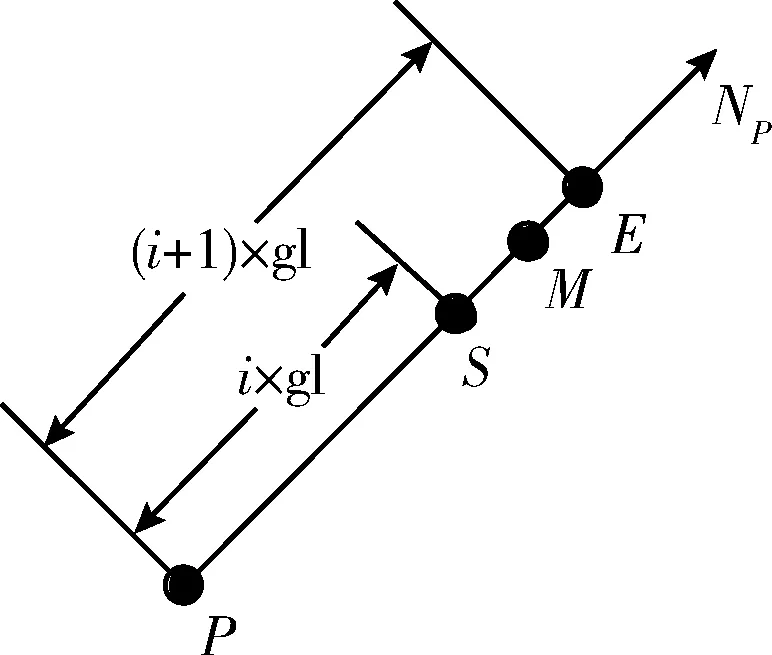
图8 样本点P的法线追踪

为了减少中轴点M的法线段的跟踪区域，使用网格单元来跟踪样本点P的法线段。因为法线段SE包含中轴点M，所以只有与法线段SE相交的网格单元才可能包含中轴点。法线段SE的长度是gl，其起始点S和结束点E必定在同一网格单元或者边相邻或点相邻的网格单元中。对于后两种情况，最多有两个或3个网格单元将分别与法线段SE相交,如图9所示。这些与SE相交的网格单元将样本点P记录为其候选样本点,以用于未来的中轴点计算。这就意味着，只有具有候选样本点的网格单元才可能包含样本点P的中轴点M。我们用链表来存储网格单元的候选样本点，以此最小化网格单元的存储成本。

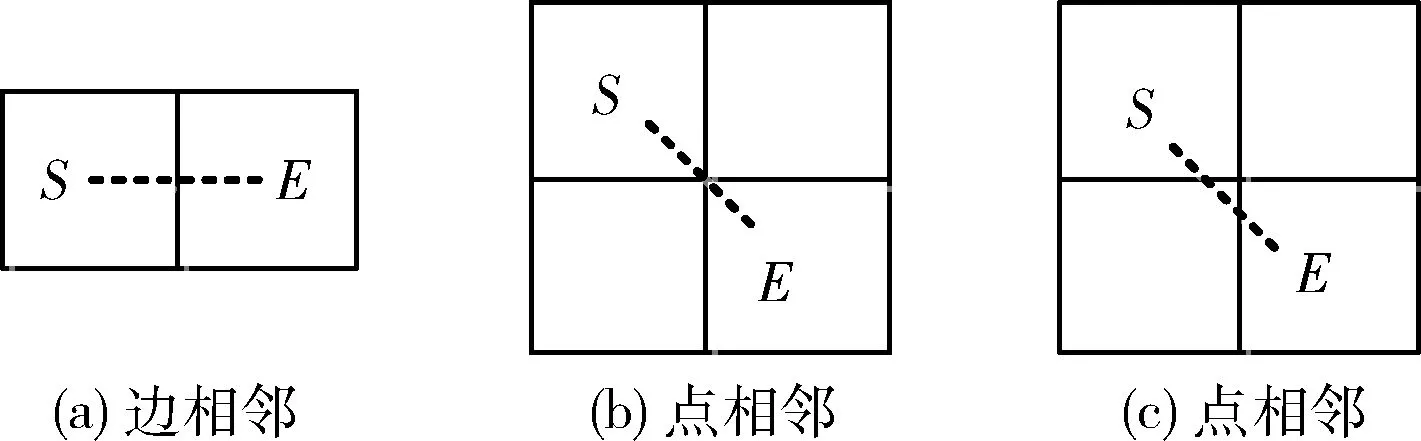
图9 与法线段相交的网络单元格

由于每个样本点的第一次法线跟踪没有相互依赖性，可以独立进行，所以可以充分利用GPU的并行计算特性，为每个样本点分配一个GPU线程来并行实现。

5.2 边界边的第二法线跟踪

在第一回合样本点P的第一次法线跟踪之后，它的中轴点M被锁定在一些网格单元中，这些网格单元将该样本点记录为其候选样本点。为了计算样本点P的中轴点M，还要再计算出样本点P的对偶边界边。由于每个边界边都可能是样本点P的对偶边界边，因而需要检查所有的边界边。

假定样本点P的对偶边界边是T，对偶边界点为Q。由于Q在边界边T上，其中轴点M一定位于边界边T的法线簇中。假设P的中轴半径在(i×gl，(i+1)×gl)中，那么在第i回合中，中轴点M必定位于当前范围的法线段簇中。因而，只有与该法线段簇相交的网格单元才可能包含中轴点M。如图10所示，边界边AB的法线段簇与4个网格单元相交，因而中轴点M一定在这4个网格中，称边界边AB是这些网格的候选边界边。对于每个网格，其可能不含有候选采样点，也可能含有一个或者多个候选采样点，则只有这些采样点有可能与边界边T构成中轴点P。

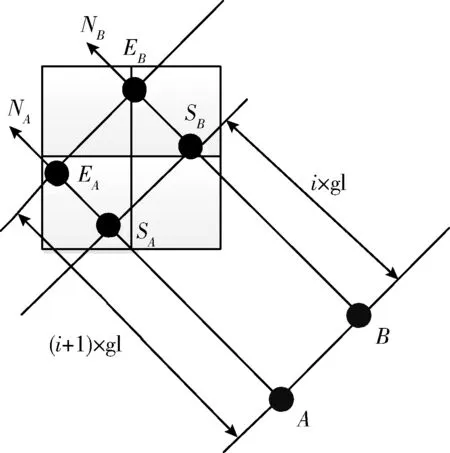
图10 与法线段簇相交的网格单元

在第i回合的两次法线跟踪后，对于每个网格都含有一些候选样本点和候选边界边。如果中轴点M在某个网格单元中，则可以通过该网格单元中的每对候选样本点和候选边界边的信息对，来计算出该中轴点。这个详细过程在5.3节中阐述。

由于不同边界边的第二次法线跟踪之间没有耦合关系,所以也可以通过为每个边界边分配一个GPU线程的方式来并行实现。

5.3 中轴点与中轴生成

在第i回合的第二次法线跟踪之后，一些网格单元中会含有一些候选样本点和候选边界边对。对于某个网格单元，它在样本点的第一次法线跟踪时，记录一些候选样本点P1，P2，…，Pn。同时，它也在边界边的第二次法线跟踪时，记录边界边T1，T2，…，Tm,作为它的候选边界边。对于这些样本点P1，P2，…，Pn,它们可能与边界边T1，T2，…，Tm上的任意一个点生成位于该网格单元中的中轴点M。假设中轴点是由样本点P和边界边T生成出的，则根据中轴定义可知，中轴点M是切点为样本点P和边界边T上的某一点的内切圆的圆心，所以下面的等式成立

M=P+NP×r=Q+NQ×r

(3)

这里，r是中轴半径，而点Q是样本点P在边界边T上的对偶边界点。通过等式(1)代替NQ，可将等式(3)转化成如下的等式

(4)

等式(4)可以转换成带有未知量x，y的如下等式

(5)

这里a1、b1、c1、d1是通过P、A和B的坐标而得出的常量。而x+y=1，此时可以通过等式(5)得到如下等式

(6)

由于等式(6)在x轴和y轴分别成立，因此可以转换成一个含有未知量r和未知量x的含有两个方程的二元方程组，其解可以方便而准确地解出。注意，r的解的数量可能多于一个，但只采纳中轴半径在当前范围的r。如果x、y和r都是非负的，则说明样本点P的对偶边界点Q在边界边T上，也可以确定采样点P的中轴点M。这里，一个样本点P可能通过不同的解得出多于一个中轴点，但是只采纳中轴半径最小的中轴点。

每回合迭代后，都有部分样本点计算出其中轴点，则下一回合无需这些采样点参与。通过多回合的迭代，最终可以计算出所有样本点的中轴点。根据样本点的拓扑连通性，可以对相应中轴点进行连接。如样本点A、B是相连的，则其对应中轴点M1和M2也需要相连。通过中轴点的连接，可以形成形状的中轴线。

6 实验与分析

为了验证算法的有效性，采取了多种不同类型的形状进行实验。实验的平台是Visual Studio2010，电脑处理器是英特尔i7-8700，显卡是英伟达GTX1050Ti。

实验共分成8组：实验1是计算由简单直线构成的凹多边形的中轴；实验2是计算由圆弧和直线构成的规则多边形的中轴；实验3是计算由直线和圆弧构成的带孔的规则多边形的中轴；实验4是计算由不规则的曲线构成的随机不规则图形的中轴；实验5～实验8则是计算较为复杂的图形的中轴。实验结果如图11所示。

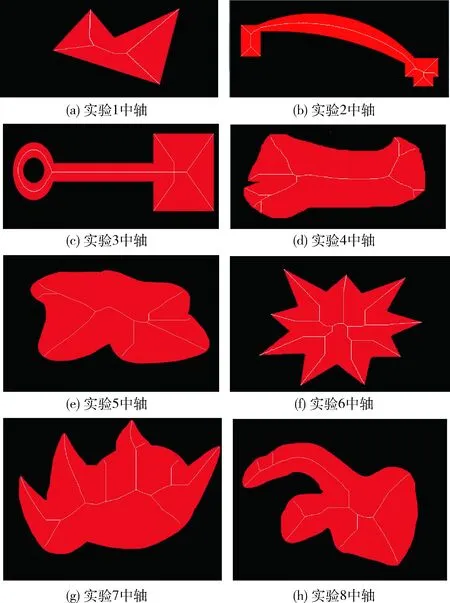
图11 形状中轴显示

经过多次的实验，可以得知，对于不同类型的形状来说，该方法都能准确找到其中轴，并有效地显示出来，可以得知该方法是有效的、精确的。

将传统的细化算法和形状分解算法与本文的算法进行比较实验，并将本文算法分别通过CPU和GPU进行比对实验，实验时间对比见表1。

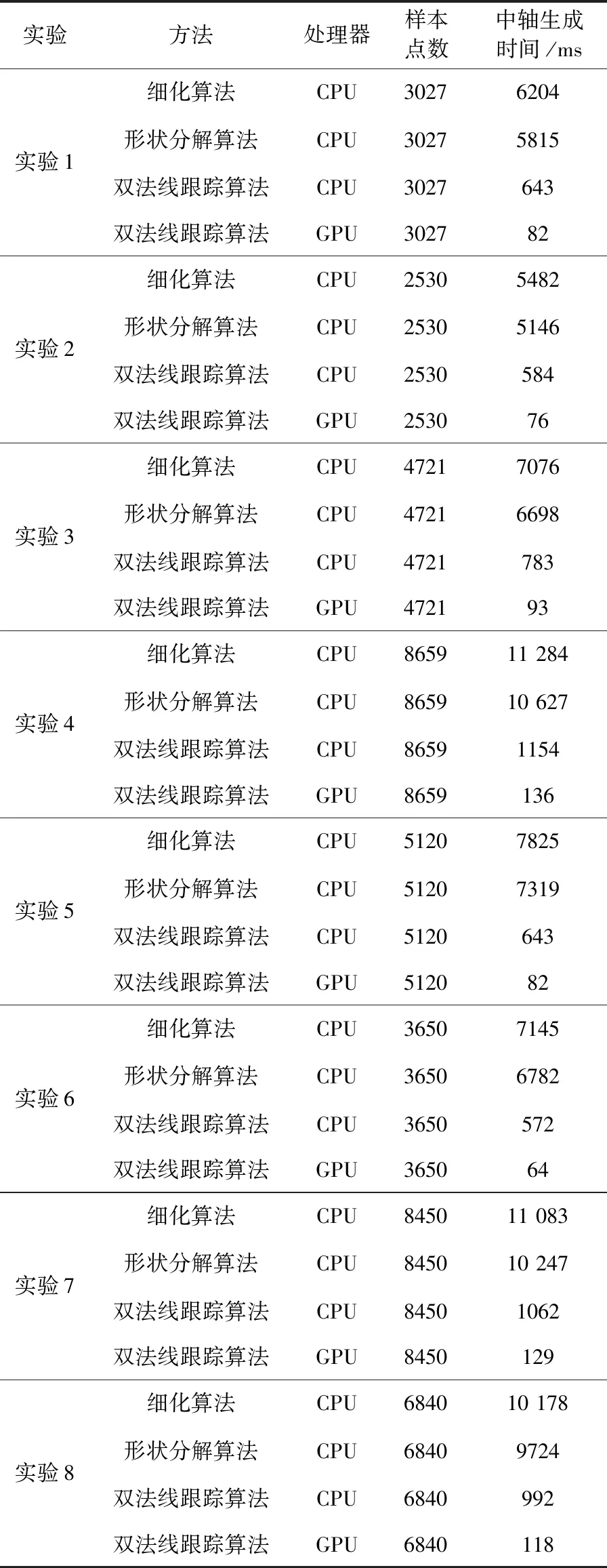
表1 实验数据

通过上面的表格,我们可以很明显看到，本文的算法比其它的算法在运行时间上有很大的提升。并且在利用GPU进行并行计算时，由于两次的法线跟踪都是并行计算的，所以花费的时间比较少。虽然理论上GPU线程多达数百个，但由于CPU线程运行速度实际比GPU线程快得多，所以GPU实际提升的效率大概在10倍左右。由此可知本文的方法是高效的。

本算法适用范围广泛，不仅可以计算规则形状的中轴，也可以计算不规则形状的中轴。在样本点较多的情况下，其离散后的多边形与原图形相似，因而其生成的中轴与真实中轴非常接近。对于只有直线段的规则图形，离散后的多边形与原始图形完全一致，边界边的法线簇和样本点的法线簇也与原始图形完全一致。由于本文的中轴点是严格按照中轴定义生成的，因而这种情况下生成的中轴即是精确中轴。由此可知本文生成的中轴是高质量的。

7 结束语

在本文中，提出了一种利用双法线跟踪来并行计算形状中轴的算法。首先，将模型分割成网格模型，并将形状边界进行离散化，估计样本点及边界边的法向。然后，对于模型的每个样本点，使用并行双法线跟踪算法生成其对应中轴点。最后，根据其对应样本点的连接性连接中轴点来生成形状中轴。本文的主要贡献在于：①利用GPU来对样本点的第一次法线跟踪和边界边的第二次法线跟踪进行并行计算，计算效率显著提高。②通过将模型的包装盒划分成网格单元，来减少并行计算中每个网格单元中候选样本点和候选边界边对的平均数量，降低了算法的时间复杂度。③将样本点按照其中轴半径来分组，在每回合迭代中，仅中轴半径在当前范围内的样本点参与中轴点计算，减少了并行计算中每个样本点的相交网格单元的平均数量，提高了算法效率。

未来的工作将会集中在将该方法合理地拓展到三维空间中，并进一步研究如何高效地将中轴线生成中轴面。