双曲螺线的副法线曲面的相关性质研究*
2015-06-19胡文丽
胡文丽,梁 林,包 弘
(楚雄师范学院数学与统计学院,云南楚雄675000)
双曲螺线的副法线曲面的相关性质研究*
胡文丽,梁 林*,包 弘
(楚雄师范学院数学与统计学院,云南楚雄675000)
本文以双曲螺线生成的曲面为研究对象,讨论了三维欧氏空间中双曲螺线的副法线曲面的几何性质,获得了双曲螺线的副法线曲面的渐近曲线、曲率线、法曲率、主曲率、高斯曲率、平均曲率、常高斯曲率曲线、极小轨迹等,并给出了简单应用。
双曲螺线;副法线曲面;第一基本形式;第二基本形式;主曲率
微分几何是以数学分析的方法为基础来研究曲线、曲面的学科,主要讨论曲线或曲面上某一点邻域的几何性质。副法线曲面的性质是近年来新的研究热点[1-3].袁媛、刘会立在文[2]中讨论了特殊曲线的副法线曲面以及由此特殊性而得到的相关结论。受此启发,本文讨论了双曲螺线的副法线曲面,给出了双曲螺线的副法线曲面的相关几何性质.
1.预备知识
副法线曲面是由曲线r→(t)的副法线生成的直纹面.设γ→(t)为曲线r→(t)上任意一点P的副法向量,则曲线r→(t)的副法线曲面∑为

相应地,曲面r→=r→(u,v)的第一基本形式、单位法向量、第二基本形式分别为
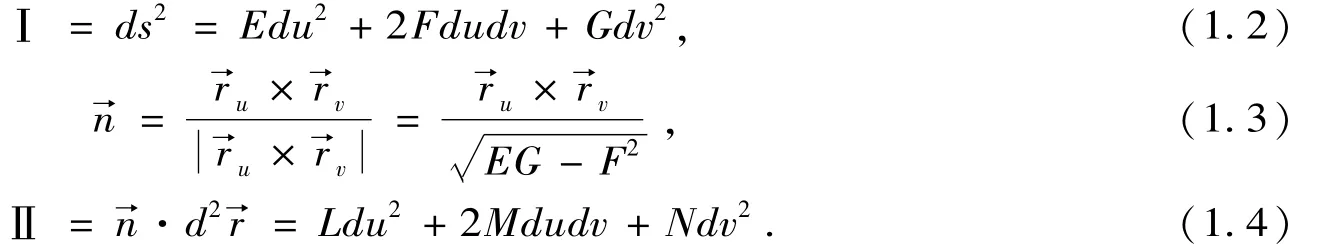
2.主要结论
定理1 双曲螺线r→(t)={a cosh t,a sinh t,at},a>0的副法线曲面的微分方程为
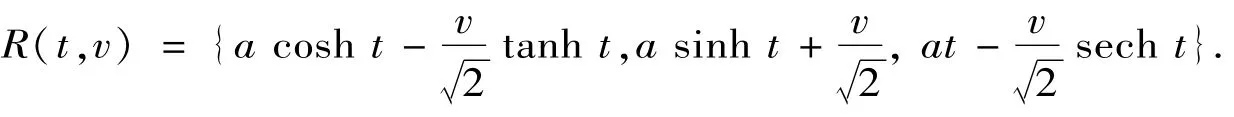
证明 由r→(t)={a cosh t,a sinh t,at}得
r→′={a sinh t,a cosh t,a},r→″={a cosh t,a sinh t,0},r→′×r→″={-a2sinh t,a2cosh t,-a2},
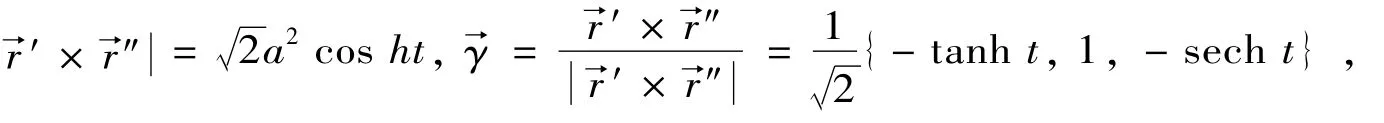
证明 由r→(t)={a cosh t,a sinh t,at}得

定理3 双曲螺线的副法线曲面的第一基本形式为


定理4 双曲螺线的副法线曲面的第二基本形式为
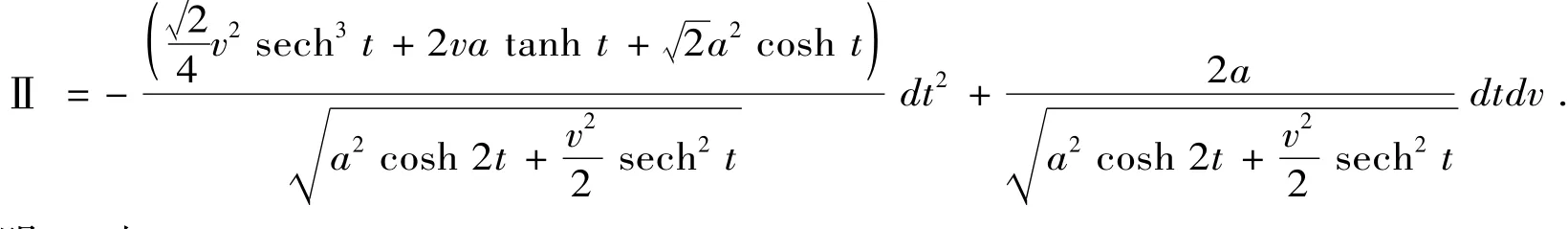
证明 由

定理5 双曲螺线的副法线曲面的渐近曲线的方程为
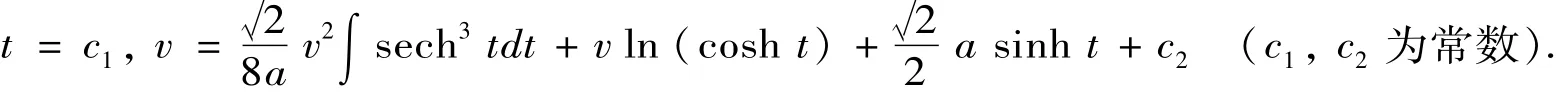
证明 双曲螺线的副法线曲面的渐近曲线为
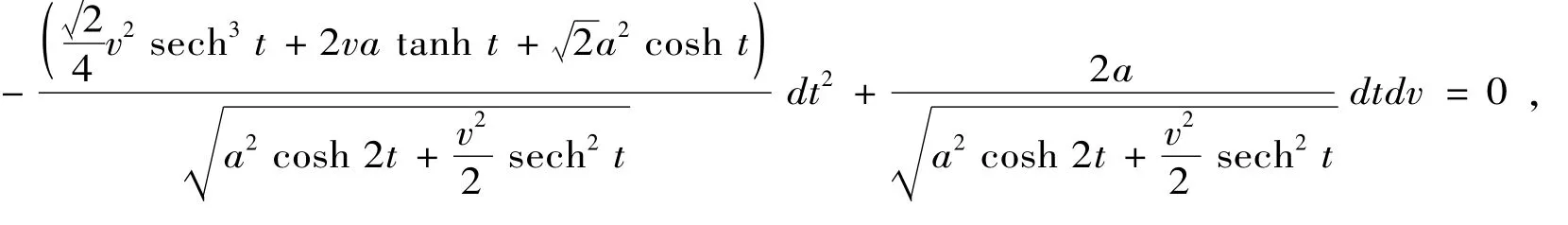
定理6 双曲螺线的副法线曲面的曲率线的微分方程为
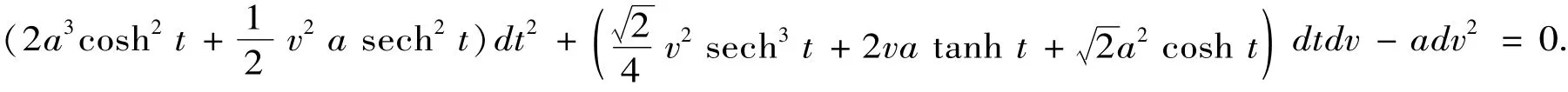
证明 双曲螺线的副法线曲面的曲率线所满足的微分方程为
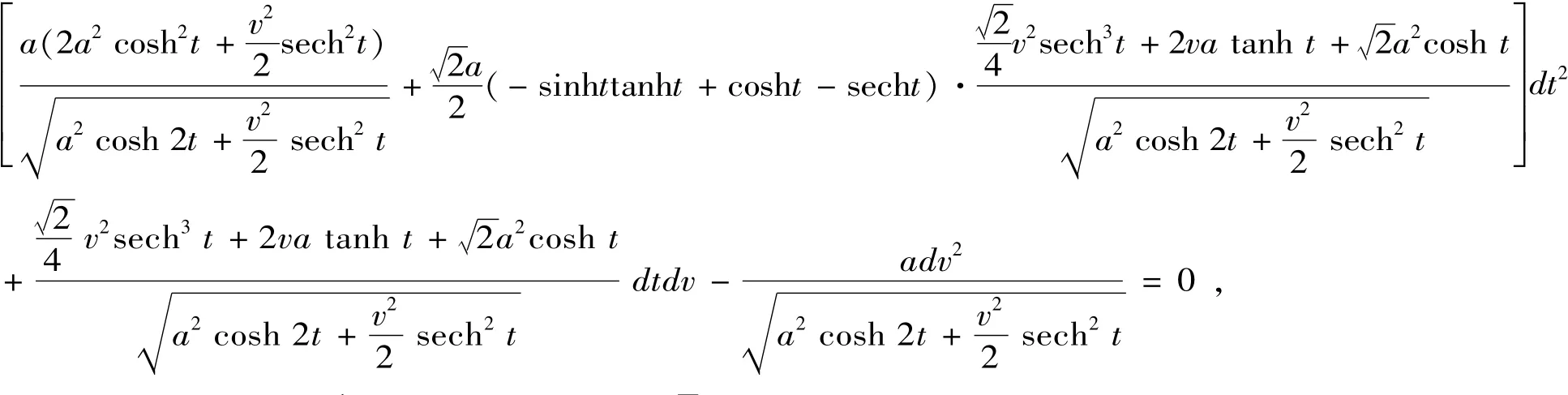
定理7 双曲螺线的副法线曲面的法曲率为
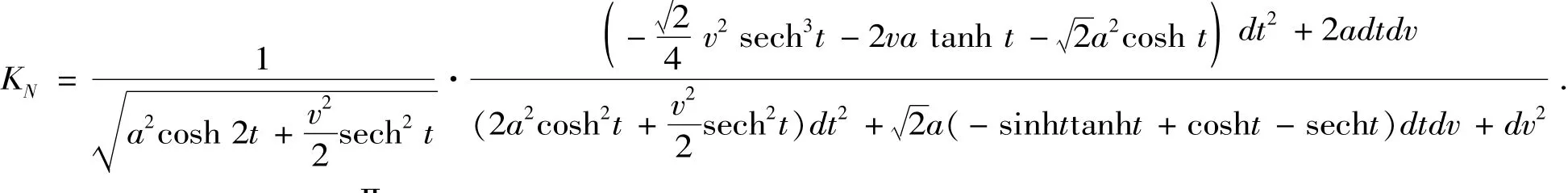
定理8 双曲螺线的副法线曲面的主曲率为
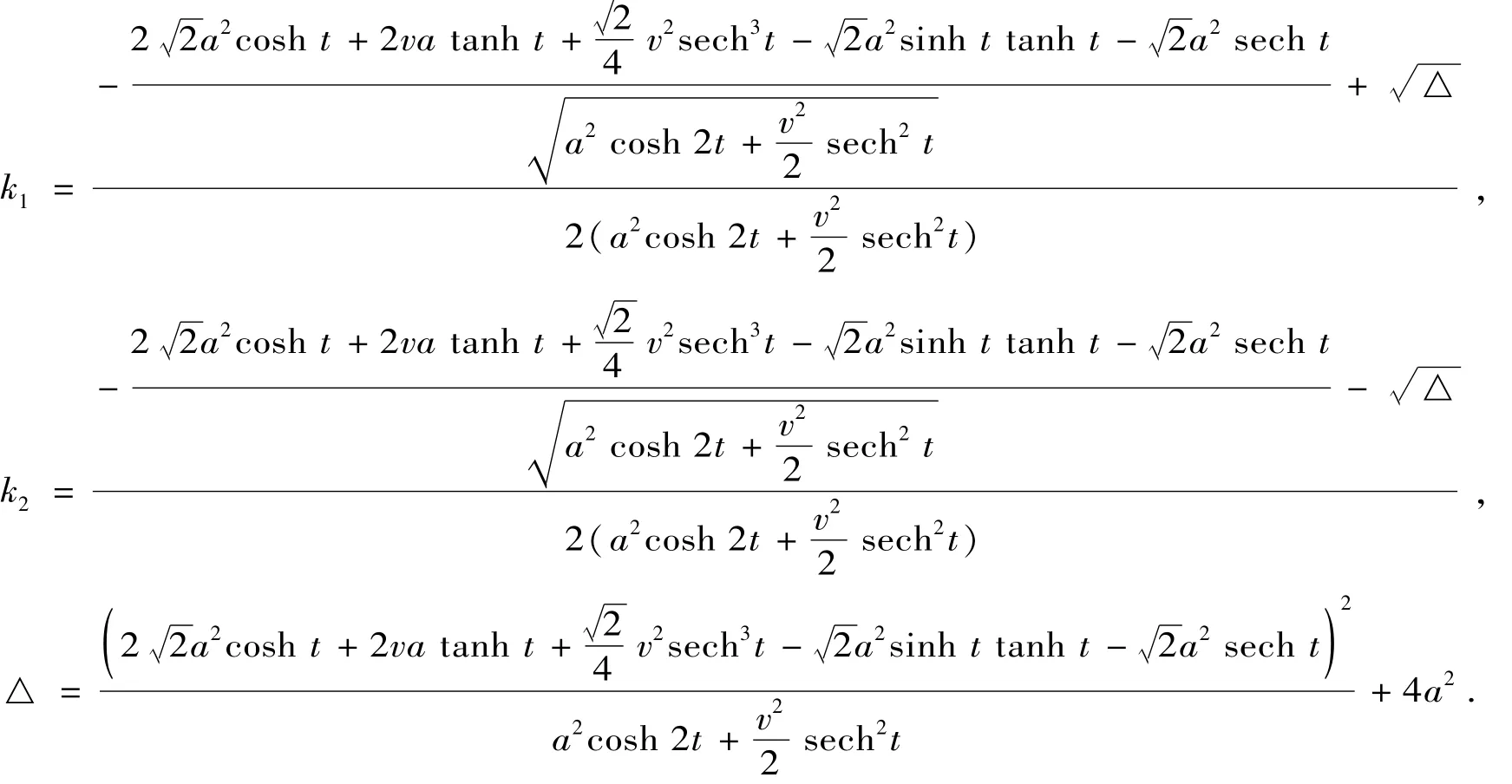
证明 由主曲率的计算公式有
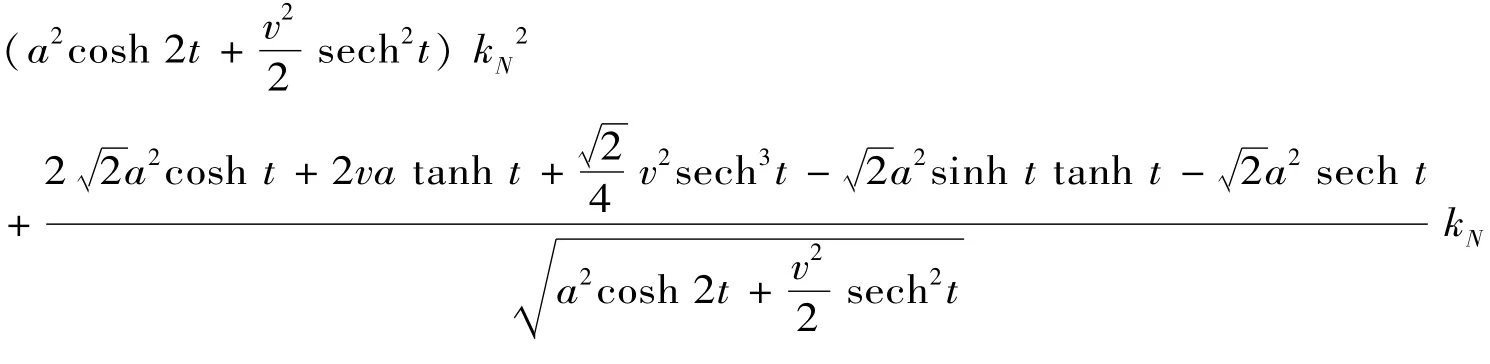
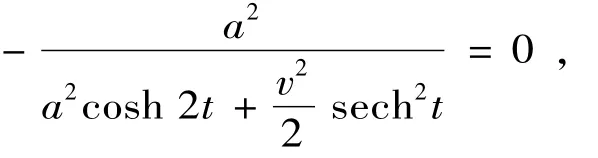
记曲面的主曲率为k1和k2,由求根公式即得.
定理9 双曲螺线的副法线曲面的高斯曲率为
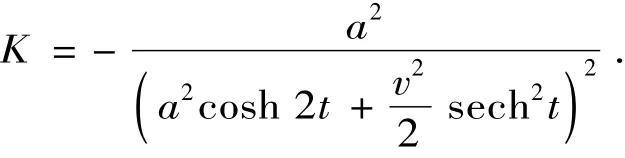
证明 双曲螺线的副法线曲面的高斯曲率K=k1k2,由定理8和韦达定理即得结论。
定理10 双曲螺线的副法线曲面的平均曲率为

定理11 双曲螺线的副法线曲面的常高斯曲率曲线为
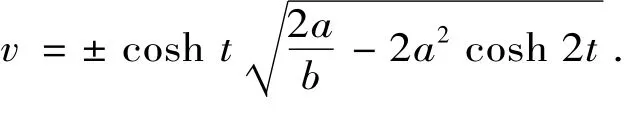
证明 设高斯曲率K=-b2,由定理9有

定理12 双曲螺线的副法线曲面的极小轨迹为
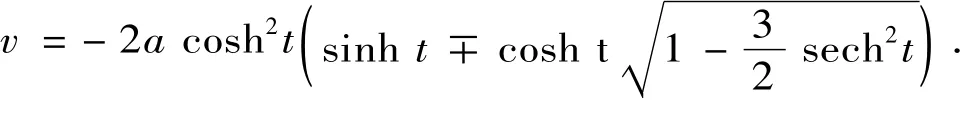
[1]梅向明,黄敬之.微分几何[M].高等教育出版社,2008.
[2]袁媛,刘会立.空间曲线的副法线曲面[J].东北大学学报,2012,33(10):1517—1520.
[3]崔风午.双曲螺线在一点的邻近结构[J].吉林师范大学学报,2014,28(3):1—5.
(责任编辑 李艳梅)
Binormal Surface Hyperbolic Spiral
HU Wenli,LIANG Lin&BAO Hong
(School of Mathematics and Statistics,Chuxiong Normal University,Chuxiong,675000,Yunnan Province)
The hyperbolic spiral as the background,surface generation as the research object,discusses the geometric properties of the Euclidean space of hyperbolic spiral binormal surface.The hyperbolic spiral binormal surface asymptotic curves,lines of curvature,curvature method,principal curvature,Gaussian curvature,mean curvature,constant Gaussian curvature,minimal path,and gives a simple application.
Hyperbolic spiral;binormal surface;First basic form;Second basic form;principal curvature
O186.1
A
1671-7406(2015)09-0009-04
2015-07-10
梁 林(1967—),男,教授,研究方向:微分几何。
