基于自适应分数阶扩展卡尔曼的锂电池SOC估算

余 鹏，王顺利，于春梅

（西南科技大学信息工程学院，四川 绵阳621010）

随着环保意识的日益增强，无污染、可循环利用的清洁能源越来越受到推广。在汽车行业，锂电池驱动的纯电动汽车将逐渐取代以汽油为燃料的传统汽车[1]。然而，精确地估算电池荷电状态(SOC)是很困难的，因为电池本身是一个高度非线性的系统，并且电池参数会随着SOC值、温度、电池老化程度等变化[2]。文献[3]提出一种基于二阶RC 模型的SOC辨识方法，未考虑模型参数随电池充放电变化的情况。文献[4]中提出基于分数阶模型的分数阶扩展卡尔曼算法估算SOC，估算结果展示了分数阶算法具有快速收敛的特性，但由于分数阶算法特性，随着历史数据的增多而造成计算负荷增大。文献[5-6]利用扩展卡尔曼算法估算电池SOC，再建立仿真模型进行精度验证，由于传统扩展卡尔曼算法(EKF)在进行非线性变换时会造成较大误差，验证结果在SOC较低时误差更大。针对电池参数的时变特性、分数阶算法计算量大以及传统EKF估算精度低的问题，本文作者提出了一种改进分数阶扩展卡尔曼算法(FEKF)，充分考虑锂电池充放电特性，采用时变参数等效电路模型表征电池充放电特性。加入记忆长度因子精简分数阶算法复杂度，考虑噪声的实时更新特性提出滑窗模型自适应噪声因子，提高了SOC估算的鲁棒性与精度

1 锂电池模型建立及参数辨识

1.1 等效电路模型

等效电路模型可用于表征锂电池外部特性和内部参数之间的关系。建立准确的电池模型是SOC估算的基础，等效电路模型的准确性将直接影响SOC估算的准确性。目前，常用的等效电路模型有Rint模 型、Thevenin 模 型 和PNGV 模 型[7]。Thevenin 模型参数相对较少，曲线拟合时为单指数数学模型，与PNGV 模型相比，后续估算过程需要较少的计算，更适合嵌入式系统的SOC估算[8]。同时，在传统Thevenin模型基础上采用时变函数刻画模型参数随SOC 的变化，它能在各个SOC 阶段为SOC 估算提供准确的模型，估算效果有很高的精度保证。Thevenin模型如图1所示。

图1 Thevenin等效电路模型Fig.1 Thevenin equivalent circuit model

图1 中，Ro为欧姆内阻；Cp和Rp分别为极化电容和极化电阻；Up是极化电容上的极化电压；Uo是电池的开路电压；UL是电池的负载电压；IL是负载电流。负载电压UL的物理方程可以结合Thevenin等效电路模型求得，如式(1)所示。

利用该电路模型能采用数学方法描述锂电池对外特征，考虑电池的充放电效率的情况下根据安时积分法和基尔霍夫定律可以分别列出SOC计算式和Thevenin电路方程[9]。

式中，η 为充放电效率；Q0为电池容量，安时积分法采用的是开环方法估算电池SOC，没有考虑对估算结果的有效修正。

1.2 模型参数辨识

利用HPPC(hybrid pulsepower characteristic)实验数据辨识出Thevenin模型中的参数值，从而使得采用该模型能有效、准确地表征实际锂充放电特征。通过HPPC实验可以获得不同SOC下的脉冲充放电电压数据，计算得到参数值见表1。

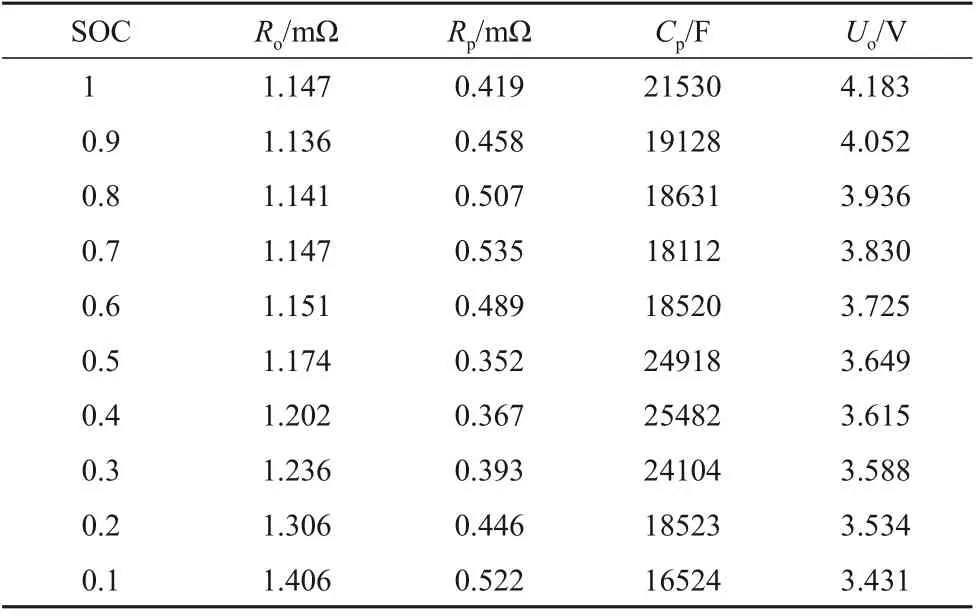
表1 参数与SOC对应值Table1 The parameter corresponding SOC

根据以上辨识结果可以拟合各参数随SOC变化的多项式曲线。

各参数与SOC的多项式关系可以表征电池使用过程中，随SOC 变化，锂电池内部结构会发生变化，从而表现出对外电气特性的变化。与利用各SOC点参数平均值建立的等效电路模型相比，考虑了电池特征的时变性，能更加精确地体现锂电池的对外物理特性。图2为开路电压Uo与SOC的多项式拟合关系图以及拟合误差。

图2(a)中蓝色曲线Uo-SOC1 是通过HPPC 实验测得的实际开路电压Uo与SOC的函数关系曲线图，红色曲线Uo-SOC2是采用四阶多项式函数关系拟合得到的Uo与SOC关系曲线。图2(b)为拟合曲线与实验结果的误差曲线，从图中可以看出通过四阶多项式拟合结果误差不超过0.03 V，说明Thevenin模型能很好地表征锂电池外特性并且四阶多项式也能准确地数学描述Uo随SOC的变化过程。

图2 Uo-SOC拟合结果Fig.2 Uo-SOC fitting results

2 改进分数阶算法理论

2.1 EKF理论

EKF算法是对经典卡尔曼算法的改进，在该方法中，将非线性空间方程在xk处进行泰勒级数展开，并且消除二阶及以上的高阶项，以获得近似线性空间方程[10]。然后将卡尔曼滤波算法应用于线性空间方程，估计当前状态值。离散非线性系统空间的状态方程和观测方程如式(4)所示。

式中，xk代表k时刻的系统状态变量；yk是k时刻观测变量；uk作为系统控制变量；A 是状态变量的状态转化矩阵；B 是输入矩阵；C 是测量矩阵；ωk是系统的过程噪声；νk是测量噪声[11]。采用EKF估算电池SOC时，上述状态方程和观测方程可以写为式(5)。

观测方程中的观测值为电池两端的端电压UL，根据Thevenin 模型中开路电压Uo、极化电压Up和内阻Ro上电压的关系求得观测方程中端电压表达式。与式(4)对比可以得出A、B、C的表达式。

然后利用分数阶导数公式对算法后续工作进行变形处理。

2.2 分数阶导数

早在1994年就有学者提出，当t=0时，将恒定的直流电压U加载在电容两端，产生一个电流i(t)=V/(htn)，其中，0＜n＜1，t＞0，h 是和电容容量有关的恒定值，这意味着电容本质是分数阶的[12]。分数阶导数实际是对整数导数的推广，常见的分数阶导数 有： Riemann-Liouville (R-L)、 Caputo 以 及Grunwald-Letnikov(G-L)分数阶导数，本文结合G-L定义设计分数阶算法做估算。G-L 定义如式(7)所示。

分数导数相较于整数导数，具有更好的全局相关性。式中，h 为位移距离；n 是导数阶数，可以扩展到任意分数导数。

2.3 改进的FEKF算法

使用G-L分数阶导数定义对EKF状态变量求分数阶导数并取采样时间为1(h=1)。

Δ 为差分算子，n 为差分阶数，结合状态方程(4)可以得到分数阶线性离散状态方程

式中，Ad=A-I(I 为单位矩阵)，式(8)和式(9)是对一维状态变量的分数阶表述，由于传统EKF状态方程式(5)采用二维状态变量所以将其推广到高维分数阶状态空间方程如式(10)所示。

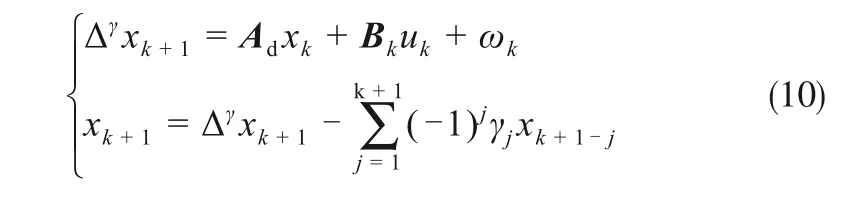
其中

γ为分数阶；n1，…，nk是分数阶的阶数；N为状态变量的维度。由传统卡尔曼滤波器定义并结合式(10)可以得到状态变量xk的一步最佳线性预测如式(12)所示。

由于经典FEKF 算法对历史数据有很强的依赖性，虽然保证了迭代算法的全局性，但在历史数据过多的情况下会出现数据饱和的情况，考虑到实验采样时间与实验时长造成的数据冗余，加入记忆长度因子M(当数据超过M时遗忘“过时”的老数据，保留离当前时刻最近的M 个数据)。同时考虑相应的自适应过程噪声与观测噪声，先对其进行数学定义。

采用滑窗思想对固定长度的输出电压误差求取均方误差，当新数据到来则替换窗口停留时间最长的老数据。根据记忆长度M=20，取窗口长度也为20，输出端电压误差计算式见式(14)。

式中，dk为噪声自适应过程中权值因子；ek是端电压的新息序列，通过定长度的历史数据计算与分数阶微分历史数据相对应的平均误差。然后计算预测协方差矩阵Pk|k-1并根据最小均方差原则计算卡尔曼增益Kk。

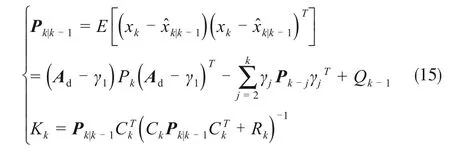
根据状态变量xk和一步最佳线性预测x^k|k-1，在获得协方差矩阵预测值和卡尔曼增益之后，更新状态变量以获得最佳状态变量值即最小均方误差估计值，同时加入自适应因子对协方差矩阵进行更新，如式(16)所示。

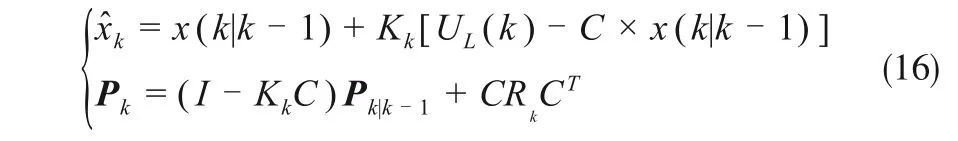
用分数阶算法实现电池SOC估计能使用观测值和状态变量的预测值不断更新系统状态变量，并通过迭代计算方法获得最优状态变量，同时加入自适应噪声因子达到噪声滤波的效果，图3为该算法流程图。

图3 算法流程图Fig.3 Algorithm flow chart

算法以扩展卡尔曼为基础，利用分数阶导数具有记忆性的特点对状态预测方程进行分数阶积分增加状态预测的全局相关性，提高状态预测的准确度。同时利用滑窗模型思想计算自适应因子Rk，将自适应因子转化到协方差矩阵以及卡尔曼增益中，提高算法精度。

3 实验验证

3.1 等效电路模型精度验证

在Matlab/Simulink 中，将模型和算法相结合，建立Thevenin 等效电路模型和SOC 估算算法，将参数数据代入算法，通过自适应迭代运算求解SOC值。图4 是对提出的Thenvenin 模型进行DST(dynamic stress test)工况验证。

图4(a)是在DST工况下模型输出电压和电池两端实际电压的对比，其中U1是实际端电压，U2是模型仿真电压。图4(b)是模型电压和真实电压的差值，从图中可以看出在DST工况中该Thevenin模型的电压误差不超过0.03 V，在电池放电末期，由于电池本身化学特性会出现较大的压降，所以电压差达到0.04 V。结果表明提出的Thevenin模型和参数辨识的结果对锂电池的表征有很高的准确度和可靠性。

3.2 算法精度验证

以上构建的时变等效电路模型可以为算法提供精确的模型基础，有效避免由于模型精度误差引起的算法估算误差。图5 是改进的FEKF 算法和EKF算法在锂电池环境温度为25 ℃时的恒流工况和DST工况下的SOC估算结果。

图4 等效模型验证Fig.4 Equivalent model verification

图5(a)、5(c)分别是恒流工况和DST 工况下使用两种算法对SOC进行估算的结果，SOC_Re是标准参考SOC 值。图5(b)、5(d)分别是两种工况下SOC 估算的误差，可以看出两种工况下改进的FEKF 算法相较于EKF 算法的估计精度更高，误差在2%以下。并且由于改进算法加入了自适应噪声，误差波动更加平滑，可以看出，该算法对SOC估算精度很高噪声滤波效果更好，对移动端的电池SOC估算具有积极意义。

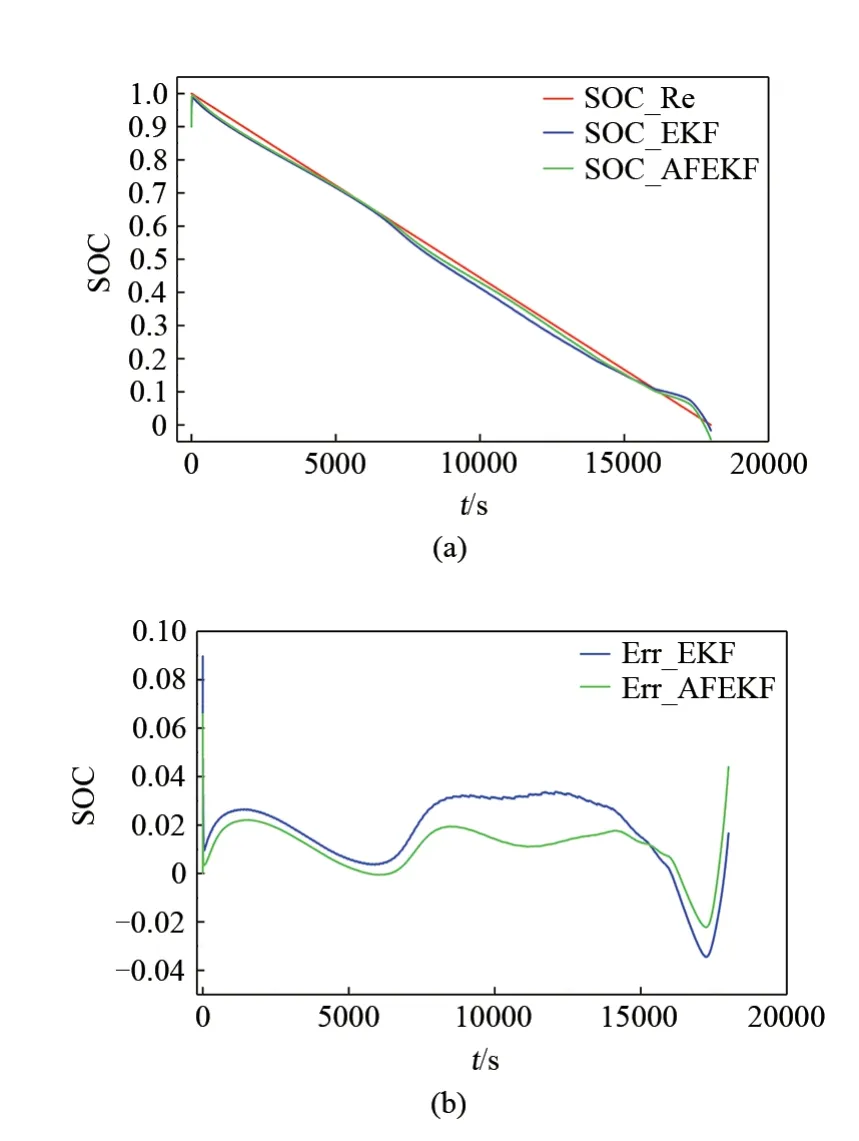
图5 不同工况下FEKF估算结果Fig.5 FEKF Estimation Results under differrent Condition

4 结 论

为了建立更精确的等效电路模型，保证SOC估计的准确性，本文提出了一种改进的参数辨识方法，采用时变的参数值表征实际锂电池特性时变的化学本质，利用参数值与SOC的多项式关系建立精确的等效电路模型。实验表明，该方法得到的等效电路模型与实际电路之间的误差小于0.03 V。采用改进FEKF 方法估算SOC，在复杂工况下的估计误差不超过2%。由于加入了记忆长度因子M 和滑窗模型，不仅计算量小而且具有较高的鲁棒性，对于锂电池状态精确估算有指导意义。