一个特殊拟算术平均的两个精确不等式*

钱 伟 茂

(湖州职业技术学院 继续教育学院, 浙江 湖州 313000)

一、研究背景

设r∈(0,1)，第一类和第二类完全椭圆积分κ(r)和ε(r)分别定义为：

一直以来，完全椭圆积分得到了比较深入的研究.关于特殊情形，国内外学者证明了许多关于第一类和第二类完全椭圆积分的重要性质和不等式.

1998年，Toader介绍了一个关于两个正数a和b的经典拟算术平均Mp,n(a,b)[2]358-368：

其中，rn(θ)=(ancos2θ+bnsin2θ)1/n.当n≠0和r0(θ)=acos2θbsin2θ时，p是一个严格单调函数.

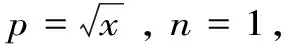
(1)

两个正数a和b的几何平均G(a,b)、算术平均A(a,b) 和反调和平均C(a,b) 分别定义如下：

(2)

并且有熟知不等式

G(a,b)

(3)

对所有a,b>0且a≠b成立.

关于特殊的拟算术平均E(a,b)的其他二元平均和其组合的比较研究，目前已取得了一定进展.钱伟茂等证明了双向不等式[3]1-10

Gp[λa+(1-λ)b,λb+(1-λ)a]A1-p(a,b)

袁琴等证明了双向不等式[4]12-16

Cα1(a,b)H1-α1(a,b)

对所有a,b>0且a≠b成立，当且仅当α1≤7/16，β1=1，α2≤4/π2，β2≥7/16，其中H(a,b)=2ab/(a+b)是两个正数a和b的调和平均.

赵铁洪等证明了双向不等式[5]1-12

对所有a,b>0且a≠b成立，当且仅当α1≤3/16，β1≥64/π2-6=0.484 5L,α2≤3/16，β2≥(5ln2-ln3-2lnπ)/(ln7-ln6)=0.503 8L.

王淼坤等证明了双向不等式[6]821-841

α1A(a,b)+(1-α1)G(a,b)

(4)

α2A(a,b)+(1-α2)H(a,b)

对所有a,b>0且a≠b成立，当且仅当α1≤3/4，β1≥8/π2，α2≤8/π2,β2≥7/8.

从不等式(3)和(4)使得

G(a,b)

(5)

对所有a,b>0且a≠b成立.

根据不等式(5)，本研究发现最佳参数λ1,λ2,μ1,μ2∈,使得双向不等式

λ1C(a,b)+(1-λ1)G(a,b)

对所有a,b>0且a≠b成立.

二、主要结果

为证明本文的主要结果，需要以下4个引理：

也是单调递增(递减)的.如果f′(x)/g′(x)是严格单调的，则上述结论的单调性也是严格的[1]10.

引理3函数

在区间(0,1)内是严格单调递增的且值域为(1/4,4/π2).

证明函数f(r)可以分解为：

(6)

其中，

设g1(r)=(2/π)2[2ε(r)-r′2κ(r)]2-r′2，g2(r)=r2.简单计算可得：

g1(0+)=g2(0)=0,g(r)=g1(r)/g2(r)，

(7)

(8)

(9)

所以，引理3容易从等式(9)和函数f(r)的单调性得到.

引理4函数

在区间(0,1)内是严格单调递增的且值域为(1/6,32/π4).

证明设h1(r)=(2/π)4[2ε(r)-r′2κ(r)]4-(1-r4)，h2(r)=2r2(3+r2).简单计算可得：

h1(0+)=h2(0)=0,h(r)=h1(r)/h2(r)，

(10)

(11)

其中，

对J(r)关于r求导可得：

(12)

其中，

(13)

从引理2(1)、2(2)、2(3)和等式(13)使得：

(14)

对所有r∈(0,1)成立.

(15)

下面给出本文的主要结果及其证明.

定理1双向不等式

λ1C(a,b)+(1-λ1)G(a,b)

对所有a,b>0且a≠b成立，当且仅当λ1≤1/4，μ1≥4/π2=0.405 2L.

证明根据G(a,b)、C(a,b)和E(a,b)是关于正数a和b对称且一阶齐次的，不失一般性，假设a>b>0.设a=1,b=[(1-r)/(1+r)]2∈(0,1).从等式(1)和(2)得到：

(16)

(17)

从等式(16)和(17)得到：

(18)

其中，函数f(r)定义在引理3.所以，定理1容易从引理3和等式(18)得到.

定理2双向不等式

对所有a,b>0且a≠b成立，当且仅当λ2≤1/6和μ2≥32/π4=0.328 5L.

证明不失一般性，假设a>b>0.设a=1,b=[(1-r)/(1+r)]2∈(0,1).从等式(16)和(17)可得：

(19)

其中，函数h(r)定义在引理4.所以，定理2容易从引理4和等式(19)得到.

从定理1和定理2可以给出如下推论：

推论设r∈(0,1)，a=1和b=r′2，则双向不等式

对所有r′∈(0,1)成立.