算术与Toader平均凸组合的单参数平均确界*
2021-01-15马春琳徐会作
马春琳, 徐会作
(1.昌吉广播电视大学 教务处, 新疆 昌吉 831100; 2.温州广播电视大学 教师教学发展中心, 浙江 温州 325000)
一、研究背景
设a,b>0且a≠b,p∈(0,1),q∈,M(a,b)是一个二元平均,则单参数平均M(a,b;p) 、q阶幂平均Mq(a,b) 、算术平均A(a,b) 、反调和平均C(a,b) 、形心平均E(a,b) 、二次平均Q(a,b)、Toader平均TD(a,b)[1]358-368分别定义如下:
M(a,b;p)=M[pa+(1-p)b,pb+(1-p)a],
(1)
(2)
(3)
(4)
近年来,国内外数学工作者得到了许多关于Toader平均与其他二元平均的重要不等式.
Barnard和Pearce等证明了λ=3/2,μ=log 2/log(π/2)=1.534 9L是使得双向不等式
Mλ(a,b) 对所有a,b>0且a≠b成立的最佳参数[2]693-699[3]289-312. 褚玉明等证明了双向不等式 C(a,b;λ) (5) 华云等证明了双向不等式 E(a,b;α) (6) 姜卫东等找到了最大值λ和最小值μ使得双向不等式 C(a,b;λ)<αA(a,b)+(1-α)TD(a,b) 对所有a,b>0且a≠b和所有α∈(0,1)成立[7]237-242. E(a,b;1/2)=A(a,b) (7) Q(a,b;1/2)=A(a,b) (8) 对所有a,b>0且a≠b成立. 根据不等式(7)和(8)可以发现最大值λ1,λ2∈[1/2,1]和最小值μ1,μ2∈[1/2,1]使得双向不等式 E(a,b;λ1)<αA(a,b)+(1-α)TD(a,b) Q(a,b;λ2)<αA(a,b)+(1-α)TD(a,b) 对a,b>0且a≠b和所有α∈(0,1)成立. 为证明本文的主要结果,需要给出相关基础知识与几个引理. 对r∈(0,1),第一类和第二类椭圆积分分别定义为: 并有: κ(r)和ε(r)满足以下等式[8]474-475: 也是单调递增(递减)的.如果f′(x)/g′(x)是严格单调的,那么上述两式也是严格单调的[8]10. 引理3函数 在(0,1)上严格单调递增且值域是(1/4,4/π-1). f2(r)=r2,f(r)=f1(r)/f2(r). 有: f1(0+)=f2(0)=0, (9) (10) 简单计算可得: (11) (12) 引理4函数 在(0,1)上严格单调递增且值域是(0,(4/π-1)2). g2(r)=r2和g(r)=g1(r)/g2(r). 有: g1(0+)=g2(0)=0, (13) (14) 简单计算可得: (15) (16) 定理1设α∈(0,1)和λ1,μ1∈[1/2,1],则双向不等式 E(a,b;λ1)<αA(a,b)+(1-α)TD(a,b) 证明根据二元平均A(a,b),E(a,b) 和TD(a,b) 是对称且一阶齐次的,不失一般性,设a>b>0. 令r=(a-b)/(a+b)∈(0,1),p∈[1/2,1],则由式(1)(2)(4)可得: (17) (18) 由等式(17)和(18)得: [αA(a,b)+(1-α)TD(a,b)]-E(a,b;p)= (19) 其中,函数f(r)定义在引理3.因此,定理1可由引理3和等式(19)得到. 定理2设α∈(0,1)和λ2,μ2∈[1/2,1],则双向不等式 Q(a,b;λ2)<αA(a,b)+(1-α)TD(a,b) 对a,b>0且a≠b成立,当且仅当 证明根据二元平均A(a,b),Q(a,b)和TD(a,b)是对称且一阶齐次的,不失一般性,设a>b>0. 令r=(a-b)/(a+b)∈(0,1)p∈[1/2,1],则由等式(1)和(3)可得: (20) 由等式(18)和(20)可得: [αA(a,b)+(1-α)TD(a,b)]-Q(a,b;p)= [2(1-α)f(r)+(1-α)2g(r)-(1-2p)2], (21) 其中,函数g(r)定义在引理4.因此,定理2可由引理4和等式(21)得到. 注:不等式(5)和(6)是定理1和定理2在α=0时的特殊情况.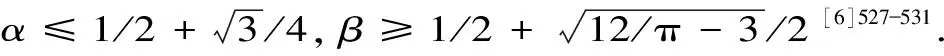

二、基础知识与引理
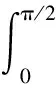




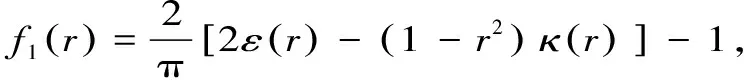
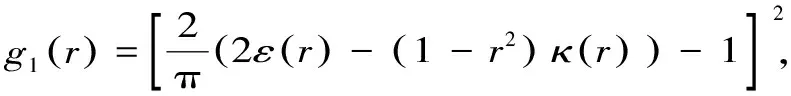
三、主要结果

