求解对称正定线性代数方程组的一个代数预处理器

刘海峰, 李正光

(1. 中山大学 数学学院(珠海), 广东 珠海 519082; 2. 吉林大学 数学学院, 长春 130012)

科学与工程中的许多计算问题最终都涉及对称正定线性代数方程组的求解. 预处理共轭梯度法是求解这类方程组的最有效迭代法, 其关键是预处理器的构造. 目前人们已构造出多种预处理器, 主要分为两类： 基于问题的预处理器和代数预处理器[1]. 一般情况下, 基于问题的预处理器比代数预处理器更有效, 但构造基于问题的预处理器需深入了解问题的背景, 利用问题的特点构造预处理器, 因此, 这类预处理器的使用范围较窄, 不具有通用性[2-6]. 代数预处理器只根据方程组的系数矩阵构造预处理器, 因此具有一定的通用性. 常见的代数预处理器有对角预处理器、 分块对角预处理器、 逼近逆预处理器及不完全Cholesky分解预处理器等[7]. 本文提出一种新的代数预处理器, 用Weyl不等式对该预处理器和分块对角预处理器进行理论分析, 并用数值算例验证所提出预处理器的有效性.

1 主要结果

考虑用预处理共轭梯度法求解如下对称正定线性代数方程组:

Kx=b,

(1)

其中K∈n×n是对称正定矩阵，b∈n是给定向量，x∈n是待求向量. 关于预处理共轭梯度法的执行过程参见文献[8].

1.1 预处理器的构造

将系数矩阵K进行如下分块:

(2)

其中A∈m×m是方阵. 受文献[9]中构造预处理器方法的启发, 本文构造如下代数预处理器W求解线性代数方程组(1):

(3)

可证明预处理器W是对称正定的[9].

1.2 本文提出预处理器的理论分析

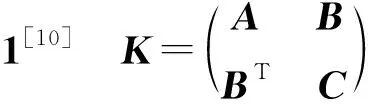
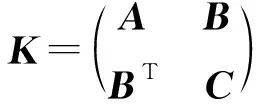
(4)

由方程(4), 有

(5)

由方程(5), 若用W作为求解方程组(1)的预处理器, 则预处理后的系数矩阵为

由Weyl不等式[11], 并结合方程(6), 有

(7)

由式(8)并结合不等式(7), 有

证毕.

1.3 分块对角预处理器的理论分析

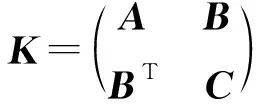
其中

若用M作为求解方程组(1)的预处理器, 则预处理后的系数矩阵为

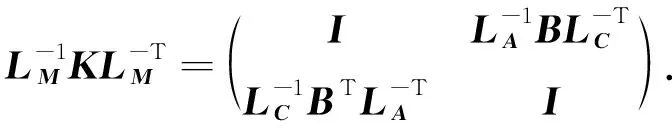
(9)

即

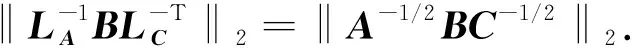
(10)

由式(9),(10)并结合引理2知结论成立, 证毕.

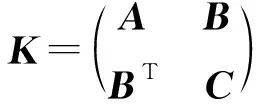
2 数值算例

考虑如图1所示的某款轿车门结构的有限元模型, 该模型刚度矩阵的维数为192 732. 用预处理共轭梯度法对该车门进行静力分析, 迭代终止条件为残量的2-范数小于10-6. 表1列出了用本文提出的预处理器、 分块对角预处理器和不完全Cholesky分解预处理器IC(0)的迭代步数和计算时间比较结果. 由表1可见, 本文提出预处理器的迭代步数和计算时间均最少, 用本文提出预处理器的计算时间约是用分块对角预处理器计算时间的77%, 是用IC(0)计算时间的20%.

图1 某款轿车门结构的有限元模型Fig.1 Finite element model of a car door structure

表1 3种不同预处理器迭代步数和计算时间的比较Table 1 Comparison of iteration numbers and computational time of three different preconditioners

综上, 本文提出了一种新的代数预处理器, 理论分析表明, 用该预处理器预处理后的谱条件数小于用分块对角预处理器预处理后的谱条件数. 数值算例表明, 用该预处理器的计算时间和迭代步数均少于用分块对角预处理器和不完全Cholesky分解预处理器IC(0)的计算时间和迭代步数.