基于出行偏好和路径长度的路径规划方法

李建伏, 王思博, 宋国平

(中国民航大学 计算机科学与技术学院, 天津 300300)

路径规划是指从道路网络中寻找从起始节点到目的节点的最优路径. 传统路径规划算法通常利用经典的图搜索算法(如Dijkstra, Floyd和A*算法)在道路网络中寻找最短路径. 但在实际应用中, 路径长度不是人们选择出行路径的唯一标准. 为使规划的路径能满足用户的实际需求, 路径规划被进一步形式化为多目标最短路径问题[1]或多约束最短路径问题[2-3], 即将用户的出行偏好建模为多个目标或约束. 但用户的出行偏好受多种因素影响, 而这些因素如何影响用户偏好未知, 甚至用户自己也无法准确地表达其出行偏好. 因此, 不能准确地描述用户出行偏好已成为限制多目标路径规划或多约束路径规划发展的瓶颈.

近年来, 随着全球定位系统(global positioning system, GPS)技术的发展及移动设备的普及, 已产生并收集了大量用户出行的轨迹数据. 轨迹数据中蕴含用户的出行偏好, 从而为获得用户的出行偏好并进一步制定最优路径规划提供了可行性. 基于轨迹的路径规划目前已成为该领域广泛关注的问题. 理想情况下, 连接任意两点的每条路径均被足够多的历史轨迹覆盖, 此时, 基于轨迹的路径规划算法只需计算每条路径的出现频次并返回频次最多的路径即可. 实际上, 大量轨迹都集中在某些局部区域, 在很多节点对之间未被历史轨迹覆盖. 因此, 现有基于轨迹的路径规划算法的基本策略是先根据历史轨迹数据中蕴含的用户偏好对道路网络重新建模, 然后再在新网络中寻找最优路径. Cui等[4]根据用户的历史轨迹数据和矩阵分解方法先构建行为-频率矩阵, 然后使用朴素Bayes模型计算路径; Jia等[5]根据用户的历史出行数据, 用深度神经网络学习用户对每条边的偏好权重向量; Chen等[6]用Markov链模型先计算出道路网络中每对节点之间的转移概率, 然后在搜索阶段将其作为流行度指标找出两节点之间的最大概率路线； Luo等[7]在文献[6]的基础上, 在指定时间区间内综合考虑后缀最优、 长度不敏感等关键属性, 提出了一种基于时间周期的频繁路径查询算法. 但上述研究均依赖于历史轨迹数据, 只适用于在被历史轨迹覆盖的区域做路径规划. 为实现在任何区域都能做路径规划, Guo等[8]提出了一种称为L2R的路径规划方法, L2R通过迁移学习将轨迹连通区域中的路由偏好转移到非连通区域, 虽能实现任意两点之间的路径规划, 但对于历史轨迹稀疏或不被历史轨迹覆盖的区域准确性较差.

由上述分析可见, 基于最短路径的路径规划算法只考虑了道路网络的拓扑结构, 而未考虑用户的出行偏好； 基于轨迹的路径规划方法则过度依赖于用户的历史出行轨迹, 当历史轨迹数据不充分时, 算法性能较差. 为充分利用历史轨迹中用户的出行偏好并更合理地规划路径, 本文将现有基于轨迹的路径规划和基于最短路径的路径规划相结合, 提出一种新的路径规划方法——2P++算法. 2P++算法与基于最短路径的路径规划相同, 即利用图搜索算法在道路网络中寻求最优路径. 2P++算法采用的图搜索算法是A*算法. 不同于现有基于最短路径的规划方法, 2P++路径规划算法的目的是能规划出一条不仅距离较短且更符合用户出行偏好的路径. 实际上, 找到满足以上两个目标的路径是一个双目标优化问题, 解决该优化问题非常耗时. 为快速找到满足上述两个目标的路径, 2P++算法使用MCMC(Markov Chain Monte Carlo)采样技术将用户的出行偏好加入到A*算法中. 此外, 2P++算法中获取用户出行偏好的方法不同于现有基于轨迹的路径规划方法, 本文采用长短期记忆模型(long short term memory, LSTM)获取历史轨迹中蕴含的用户出行偏好.

1 预备知识

1.1 基本定义

在路径规划中, 道路网络通常表示为有向图G=(V,E), 其中:V={v1,v2,…,vn}表示n个节点的集合,vi为道路交叉点或道路终点, 本文混淆使用i或vi表示节点；E={e1,e2,…,em}表示m条边的集合,ek=(i,j)(i,j∈V)表示从节点vi到vj的有向路段,ek的权重记为cost(i,j). 路径规划的目的是寻找网络G中从起始节点O到目标节点D的最优路径. 从O到D的路径PO→D是节点序列, 其中两个相邻节点通过一条边连接. 路径P的长度记为len(P). 轨迹T是移动对象的行进过程在地理空间中生成的GPS序列, 通常由一系列按时间顺序排列的位置点表示, 即T={(x1,t1),(x2,t2),…,(xl,tl)}, 其中xj(1≤j≤l)是移动对象在tj(1≤j≤l)时刻的位置.

1.2 长短期记忆模型

循环神经网络(recurrent neural network, RNN)[9]是一种前馈神经网络, 适用于对序列数据建模, 并已广泛应用于自然语言处理、 语音识别、 车辆路线预测[10]等领域. 在RNN中, 一个节点在当前时刻的输出不仅受当前输入的影响, 而且还受先前时刻输出的影响, 历史决策信息被保留在网络的隐藏状态中. 从网络结构看, RNN非常适于学习序列之间的长期依赖关系, 但由于训练过程中梯度消失和梯度爆炸问题, 传统RNN无法捕获序列中的长期依赖关系.

为解决梯度消失或梯度爆炸问题, 目前已提出了许多改进算法, 其中LSTM[11]应用最广泛. LSTM和RNN具有相同的链式结构, 不同之处在于LSTM在RNN基本单元中增加了输入门it、 遗忘门ft、 输出门ot和记忆单元ct. 门控制单元通过打开和关闭门结构决定存储什么及何时允许读、 写和擦除操作. LSTM单元各部分状态更新公式为

其中Wi,Wf,Wo,Wc为权重矩阵，bi,bf,bo,bc表示偏置向量，tanh和σ为标准激活函数，xt表示t时刻的输入向量，ht表示t时刻隐藏层的输出向量.

1.3 A*算法

A*算法[12]是基于启发式的图搜索算法. A*算法的基本思想是从起始节点开始, 优先扩展当前最有希望最快到达目的节点的节点, 直到得到目的节点或所有节点都已扩展. A*算法定义了一个评估函数f(x)=g(x)+h(x)衡量节点x的“有希望”程度, 其中g(x)表示从起始节点到节点x实际路径的代价值,h(x)表示从节点x到目的节点最优路径的代价估计值. 当被搜索图中的节点数为n时, A*算法中每次扩展节点的时间复杂度为O(n2), 最差情形下, 整个A*算法的时间复杂度为O(n3)[13].

1.4 MCMC采样技术

MCMC主要用于对复杂数据采样, 常用的MCMC采样技术是Metropolis-Hastings. Metropolis-Hastings的基本思想是先从样本空间S中随机选择一个样本作为初始状态s0, 然后根据下列迭代过程构造一个Markov链： 在第i次迭代中, 随机选择一个样本x作为候选采样点, 并根据下式计算x的接受概率π, 即x将以概率π被接受为下一个采样点si，表示为

π=min{1,p(x)/p(si-1)},

(6)

其中p(x)和p(si-1)分别表示x和si-1的出现概率. 当Markov链的长度设为a时, 将重复上述过程a次后获得的sa作为最终采样点. 接受概率π的定义决定了采样点的特点,π通常根据实际应用采用不同的定义.

2 2P++算法

2P++算法主要包括以下两个模块：

1) 用LSTM模型从轨迹数据中获取用户的出行偏好；

2) 借助MCMC采样技术将用户的出行偏好引入A*算法中, 在道路网络中寻找一条既短又符合用户出行偏好的路径. 为方便, 在2P++算法中将利用A*和MCMC搜索最优路径的过程称为A*_MCMC. 2P++算法的框架结构如图1所示.

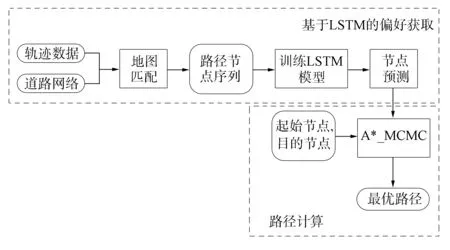
图1 2P++算法的框架结构Fig.1 Framework of 2P++ algorithm

2.1 基于LSTM的出行偏好提取

在路径规划中, 下一个节点的选择不仅取决于当前节点, 还取决于先前节点, 即路径上节点之间存在长期依赖关系. 受LSTM的启发, 本文提出一种基于LSTM的从历史轨迹数据提取偏好的方法.

构建该LSTM偏好提取过程如下：

1) 选用HMM地图匹配算法[14], 将车辆轨迹T={(x1,t1),(x2,t2),…,(xl,tl)}匹配到道路网络G中相应的路段上, 得到路径P={v1,v2,…,vt};

2) 将G中的每个节点均编码为n维独热编码, 其中n是G中节点个数, 并将匹配好的路径表示为编码序列;

3) 将与路径相对应的编码序列输入到LSTM模型中, 用以训练LSTM模型. 本文将softmax层作为LSTM模型的输出层, 输出层中有n个神经元, 每个神经元对应于道路网络G中的一个节点, 因此, LSTM模型的输出是n维向量(Pr(v1),Pr(v2),…,Pr(vn)), 其中Pr(vi)表示节点vi选为局部路径P下一个节点的概率.

训练结束后, 根据Pr(x)=Pr(vi+1|vo→vi), 使用LSTM模型预测每个节点x作为局部路径P(v0→vi)下一个节点vi+1的概率. 在LSTM中, 循环网络中一个循环单元前向传播的时间开销[15]为O(n2), 其中n是输入的维数, 即本文道路网络中的节点数. 对于包含t个节点(t≪n)的局部路径P, 使用LSTM预测局部路径P下一个节点的时间复杂度为O(n2).

2.2 基于A*和MCMC的路径搜索算法

A*_MCMC遵循基本A*算法的框架, 即从当前所有待扩展节点中不断选择节点x进行扩展, 直至找到目的节点或所有节点都已扩展为止. A*和A*_MCMC的主要区别在于选择下一个要扩展节点的方法: A*算法直接选择具有最小f(x)值的节点x; 而A*_MCMC使用Metropolis-Hastings根据接受概率π选择扩展节点x, 使节点x不仅有较小的f(x)值, 并且被LSTM预测作为当前路径下一个节点的概率值Pr(x)较高.

在Metropolis-Hastings中, 接受概率π决定了采样点的特征. A*_MCMC接受概率π定义为

(7)

其中，Pr(x)和Pr(si-1)分别表示x和si-1节点被LSTM预测作为当前路径下一个节点的概率，f(x)和f(si-1)分别表示按A*算法计算的节点x和si-1的评估函数值. 当节点x具有更低的f(x)值、 更高的Pr(x)值时,x被选择作为下一个扩展节点的概率增加.

算法1MCMC(OPEN,a).

输入： OPEN表, 采样次数a;

输出： 扩展节点;

步骤1) if (OPEN表长度为1)

步骤2) return OPEN表中节点;

步骤3) if (OPEN表长度≥2)

步骤4) 选取OPEN表中f值最小节点s0;

步骤5) fori=1 toa

步骤6) 在OPEN表中随机选取节点x；

步骤7) 根据式(7)计算接受概率π；

步骤8) if (π>rand(0,1));

步骤9)si←x;

步骤10) elsesi←si-1;

步骤11) End for;

步骤12) returnsi.

算法1给出了通过Metropolis-Hastings选择下一个扩展节点的过程, 其中所有待扩展节点均存储在OPEN表中,a为Markov链的长度. 根据算法1, 时间开销主要为从OPEN表中选择f(x)最小的节点(步骤4))和节点采样过程(步骤5)～11)). 在步骤4)中, 最坏情形下, 在OPEN表中找到具有最小f的节点的时间复杂度为O(n), 其中n是G中节点的数量. 在步骤5)～11)中, 使用LSTM预测节点x作为局部路径PO→x下一个节点的概率Pr(x)的时间复杂度为O(n2). 经过a次采样, 计算接受概率并获取采样点的时间复杂度为O(an2), 通常a≪n. 因此, 通过MCMC选择下一个要扩展的节点的时间开销为O(n2).

算法2A*_MCMC.

输入： 道路网络G, 起始点O, 目标点D,采样次数a;

输出： 路径PO→D;

步骤1)f(O)←g(O)+h(O);

步骤2) OPEN←{O};

步骤3) CLOSE←{ };

步骤4) while OPEN表不为空do

步骤5)x←MCMC(OPEN,a);

步骤6) OPEN表中删除x节点并放入CLOSE表中;

步骤7) for eachxc∈Neighbor (x)/*扩展x的邻接节点*/

步骤8) if (xc==D)转步骤19);

步骤9) elseg_t←g(x)+cost(x,xc);h_t=h(xc);

步骤10) if (xc∉OPEN)

步骤11)g(xc)←g_t;h(xc)←h_t;f(xc)←g_t+h_t;

步骤12) 将xc加入到OPEN表中;

步骤13) 根据LSTM计算Pr(xc);

步骤14) if (xc∈OPEN)

步骤15) if (g_t

步骤16)g(xc)←g_t;h(xc)←h_t;f(xc)←g_t+h_t;

步骤17) 根据LSTM计算Pr(xc);

步骤18) End for

步骤19) 从D沿父节点回溯直至O，得到路径PO→D;

步骤20) returnPO→D.

算法2给出了A*_MCMC的伪代码. 首先, 计算起始节点O的代价值f(O)(步骤1)); 然后, 将O置于OPEN表中, 并将CLOSE表初始化为一个空列表(步骤2),3)). 步骤4)～18)是路径搜索的迭代过程, 整个搜索过程分为两部分: 第一部分根据算法1从OPEN表中利用MCMC采样选择下一个扩展节点x(步骤5),6)); 第二部分是扩展节点x, 即生成x的邻接节点xc(步骤7)～18)). 根据算法1, 通过MCMC选择下一个扩展节点的时间开销为O(n2). 对于x的邻接节点xc, 生成xc的时间开销是OPEN表的遍历过程(步骤10)～17)). A*算法每次扩展节点的时间复杂度为O(n2), 则最差情形下, 扩展x节点的时间复杂度为O(n2). 最多可进行n次节点扩展, 因此, 整个A*_MCMC的时间复杂度为O(n3), 与A*算法具有相同的时间复杂度.

3 实验分析

3.1 基本数据

为检验本文算法的有效性, 下面通过实验将2P++算法与L2R算法[8](经验路径算法)和基于A*算法的最短路径规划算法(简称A*)进行比较.

实验中使用的数据主要为北京市某区域的电子地图及该地区2012-04的23 800条出租车轨迹. 该道路网络包括302个节点和586条边. 在不同时间段, 城市道路网络中的交通状况不同, 驾驶员将根据其驾驶经验相应地调整出行路线. 因此, 规划路径时需考虑时间这一重要因素. 根据北京市道路交通的特点, 将一天分为高峰时间段和非高峰时间段. 高峰时间段包括7:00—10:00和16：00—20:00, 其余时间为非高峰时间段. 历史轨迹数据分为两部分： 一部分包括在高峰时间段出现的9 500条轨迹； 另一部分包括在非高峰时间段出现的14 300条轨迹. 实验中分别对比在高峰和非高峰时间段3种算法的性能.

为测试算法在历史轨迹密集和稀疏情形下的性能, 本文根据车辆轨迹分布先将路网分为轨迹密集区域和轨迹稀疏区域, 再分别从轨迹密集和稀疏区域中各选择10对起始节点和目标节点对(简称OD对). 对来自轨迹密集区域的10个OD对按它们之间距离从短到长的顺序依次进行1～10编号, 对来自轨迹稀疏区域的另外10个OD对按距离从短到长的顺序依次进行11～20编号. 实验中, 将20个OD对作为3种路径规划算法的输入, 然后分别比较每种算法对每个OD对返回路径的准确度、 长度和行程时间.

3.2 路径准确度对比

规划路径P的准确度定义为P与真实路径P*的相似度. 相似度越高, 路径规划算法的准确性越好. 用文献[16]中定义的路径相似度函数pSim(P,P*)计算规划路径P与真实路径P*之间的相似度, 计算公式为

(8)

3种算法针对20个OD对得到的路径准确度如图2所示, 其中: (A)为算法规划高峰时间段路径的准确度； (B)为算法规划非高峰时间段的准确度.

图2 3种算法在不同时间段的准确度对比Fig.2 Comparison of accuracy of three algorithms in different time periods

由图2可见: 1) 无论是高峰时间段还是非高峰时间段, 2P++算法在轨迹密集区域(前10个OD对)与轨迹稀疏区域(后10个OD对)的准确度基本相同, A*算法结果类似. 表明A*和2P++算法相对稳定, 不易受历史轨迹数据分布的影响. 2) L2R算法在轨迹密集区域的准确度明显高于其在轨迹稀疏区域的准确度, 表明L2R算法高度依赖于历史轨迹的分布, 与L2R算法的本质一致, 即当一对节点之间存在轨迹时, 返回最流行轨迹中包含的路径. 此时, L2R算法获得的路径必然与流行路径最相似. 因此, L2R具有最高的精度. 当节点之间的一些轨迹不是流行轨迹或它们之间没有轨迹时, L2R通过偏好迁移学习方法推断它们之间的路径, 并与它们之间的部分最短路径进行拼接, 从而降低了L2R算法的在轨迹稀疏区域的准确性. 3) 在整体上, 无论是高峰时段还是非高峰时段, 对于所有20个OD对, L2R和2P++算法的准确度均高于A*算法, 表明从历史轨迹中提取的驾驶经验有效地指导了路径规划； 对于来自轨迹密集区域的节点, L2R算法比2P++算法更准确； 对于来自轨迹稀疏区域的节点, 2P++算法比L2R算法更准确.

3.3 路径长度对比

表1列出了A*,L2R和2P++ 3种算法针对20个OD对在高峰时间段和非高峰时间段返回路径的平均长度.

表1 3种算法在不同时段的平均路径长度(m)Table 1 Average path lengths (m) of three algorithms in different time periods

由表1可见： 1) 由于未考虑历史经验信息, 所以A*算法在高峰时间段和非高峰时间段的路径距离相同; L2R和2P++算法在高峰时段规划的路径比非高峰时段更长, 与人们倾向于在高峰时间段选择绕路行驶以避免道路拥堵的事实相符. 2) 相对于2P++和L2R算法, A*算法的路径最短, L2R算法在高峰时段和非高峰时段计算的路径长度相对于A*算法计算的路径长度分别延长了12%和7.6%, 2P++算法在高峰和非高峰时段计算的路径长度相对于A*算法计算的路径长度分别延长了7.4%和4.1%. 这是由于L2R和2P++算法通常选择经验路段, 因此路径较长. 但2P++算法规划出的路径比L2R算法更短, 与L2R算法计算的路径相比, 2P++算法在高峰时间段和非高峰时间段的路径长度分别缩短了4.2%和3.4%.

3.4 行程时间对比

3种算法对20个OD对规划路径的行程时间如图3所示, 其中: (A)为3种算法在高峰时间段规划路径的行程时间； (B)为3种算法在非高峰时间段规划路径的行程时间. 路径的行程时间越短, 算法越好.

图3 3种算法在不同时段的路径行程时间对比Fig.3 Comparison of route travel time of three algorithms in different time periods

由图3可见： 1) 无论是高峰时间段还是非高峰时间段, 3种算法规划路径的行程时间均随起始点和目的点之间距离的增加而增加. 2) 对于非高峰时间段(图3(B)), 无论是轨迹密集区域的节点还是轨迹稀疏区域的节点, 在起始点与目的点距离较短时(OD对1～5), A*算法规划路径的行程时间少于L2R算法和2P++算法. 但随着路径长度的增加, A*算法趋于花费更多的行程时间, 这是由于在非高峰时段, 道路上车辆较少且相对畅通, 当行驶距离较短时行程时间更具优势. 3) 对于高峰时间段(图3(A)), 无论是轨迹密集区域节点还是轨迹稀疏区域节点, 除编号为1,2,11的OD对外, 在其他17个OD对上, L2R和2P++算法的行程时间均远优于A*算法, 2P++与L2R算法返回路径的行程时间相近.

为更准确地展现3种算法得到规划路径的行程时间, 表2列出了3种算法得到20条规划路径的总行程时间. 由表2可见, 无论在高峰时段还是非高峰时段, 2P++和L2R算法均比A*算法好, 且2P++算法略优于L2R算法. 比较表1和表2可见, 最短路径不一定具有更快的行程时间, 这主要是因为在日常出行时, 人们倾向于选择道路条件更快捷的路线, 而不是最短的路径.

表2 3种算法在不同时段的总行程时间(min)Table 2 Total travel time (min) of three algorithms in different time periods

上述结果表明： 在轨迹数据稀疏的区域, 2P++算法的路径准确度优于L2R算法和A*算法； 在轨迹数据密集的区域, 2P++算法的路径准确度低于L2R算法, 高于A*算法; 对于平均路径长度, 无论在高峰时段还是非高峰时段, 2P++算法性能均优于L2R算法, 而低于A*算法; 对于总行程时间, 2P++算法均优于A*和L2R算法. 因此, 2P++算法更稳定, 并且其规划路径具有较高的准确度、 较短的行驶距离和行程时间.

综上所述, 针对现有路径规划方法不能同时考虑路径长度和用户偏好的问题, 本文将基于轨迹的路径规划方法和基于最短路径的路径规划方法相结合, 提出了一种新路径规划方法——2P++算法. 2P++算法首先使用LSTM模型训练轨迹数据并获取用户的出行偏好, 然后使用MCMC采样技术将获取的出行偏好加入到A*算法的搜索过程中, 使规划的路线能在距离较短的基础上更符合用户的出行偏好. 理论分析表明, 2P++算法与A*算法的时间复杂度相同. 实验结果表明, 2P++算法更稳定, 且其规划的路径具有较高的准确度、 较短的行驶距离和行程时间.