人行悬索桥地震响应分析

刘小会，许 杨，陈思甜，徐略勤

(重庆交通大学 土木工程学院，重庆 400074)

0 引 言

人行悬索桥构造简单、自重轻，但结构柔性大、非线性突出，地震作用下各构件的受力情况复杂。薛晓峰等[1]通过在大跨径人行悬索桥上设置中央扣和抗风缆来提高静风失稳临界风速；刘朝福等[2]和熊耀清等[3]研究了大跨径人行悬索桥的自振特性，发现小跨窄悬索桥的自振频率比大跨悬索桥的高。目前，国内的研究大多为对悬索桥自振特性、静风稳定性和人致振动[4]等的分析，而对抗震的分析较少。笔者以重庆市城口县人行悬索桥为对象，研究其抗震特点及规律，找出最不利位置，提出优化方案。研究结果可为此类悬索桥的抗震设计提供参考依据。

1 工程概况

重庆市城口人行悬索桥结构立面布置如图1。桥梁总长389 m，单跨跨径布置7 m搭接平台 + 382 m钢管桁架加劲梁，主缆成桥矢高23.04 m，矢跨比1/18.05，吊索间距7.20 m；加劲梁采用钢管桁架结构体系，标准节段长度均为7.2 m，桥面宽度从跨中3.6 m按线性变化到桥头5.2 m，跨中桥面与桥头桥面高差为0.6 m，纵坡坡度为0.3%。抗风索采用钢丝绳；西侧布置型钢钢骨架隧道式锚碇，东侧布置型钢钢骨架锚碇；主缆通过主索鞍座后经过散索套固定到锚碇上。

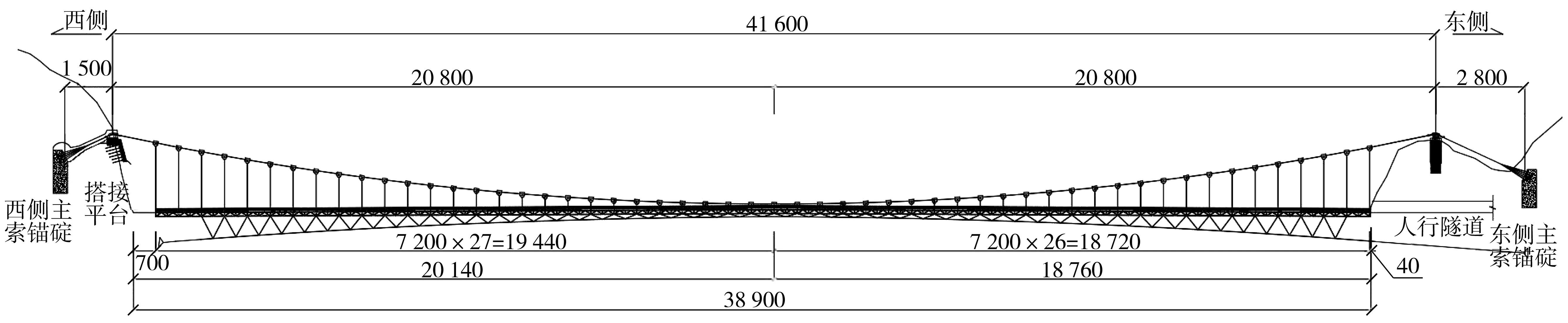
图1 城口人行悬索桥立面布置(单位：cm)Fig. 1 Layout of Chengkou pedestrian suspension bridge

2 结构动力特性分析

结构动力特性分析是后续进行地震响应分析的基础，通过结构动力特性分析可以得到结构的自振频率和振型。笔者采用子空间迭代法对城口人行悬索桥进行动力特性分析。结构前20阶的频率和振型特征见表1，前6阶振型如图2。

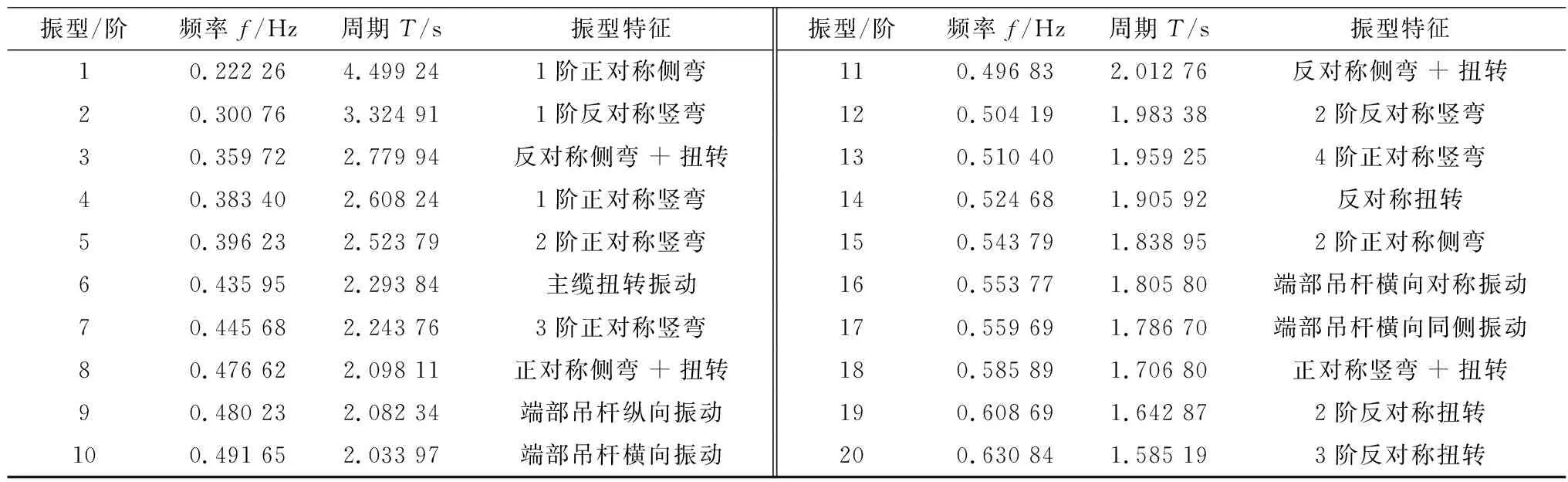
表1 城口人行悬索桥动力特性Table 1 Dynamic characteristics of Chengkou pedestrian suspension bridge

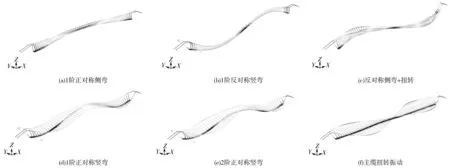
图2 城口人行悬索桥前6阶振型Fig. 2 First six vibration modes of Chengkou pedestrian suspension bridge

由图2及表1可见：

1)城口人行悬索桥整体结构柔软，各阶振型对应的频率较为接近，且频率分布密集。表明各振型之间发生耦合的概率较大。

2)第3阶振型出现了弯扭耦合振动，扭转振型出现较早，前20阶扭转振型出现频率较高，说明城口人行悬索桥的抗扭刚度较低。分析原因，加劲梁采用的是半径远大于壁厚的薄壁圆钢管结构，这种等效截面较小的细长圆钢管结构，其抗扭刚度也较小。

3)前5阶振型中，侧弯出现2次，竖弯出现3次，且以桥面系加劲梁振动为主。表明城口人行悬索桥对横向振动和竖向振动都比较敏感。因此，抗震分析中应充分考虑横向、竖向地震作用对结构的影响。

3 地震反应谱分析

3.1 城口人行悬索桥桥址设计反应谱

反应谱法即利用结构模态的正交性，将多个自由度结构体系的复杂振动分解为各个单自由度振动的叠加，从而将复杂的动力学问题转化为拟静力问题，最终求得地震动反应最大值。

由于在0.222 26～0.630 84 Hz的狭窄频率范围内激起了20阶振型，振型分布密集，因此，笔者选用完整二次项组合法(即CQC法)进行振型组合，取前300阶振型进行振型叠加计算，以考虑高阶振型对计算精度的影响。

根据国家地震烈度区划分，重庆地区抗震设防烈度为6度，地震动加速度峰值为0.05g，因此笔者在分析时，城口人行悬索桥按7度设防，地震动加速度峰值A=0.1g，桥梁类型属C类，桥址处于I类场地第二组，结构阻尼比取0.02。按照JTG/TB 02-01—2008《公路桥梁抗震设计细则》确定城口人行悬索桥的设计反应谱参数，见表2。

表2 设计反应谱参数Table 2 Design response spectrum parameters

笔者选用50年3%超越概率(E2)的地震动对结构进行地震响应分析计算。由表2设计反应谱参数计算得到E2地震设计加速度反应谱曲线，如图3。

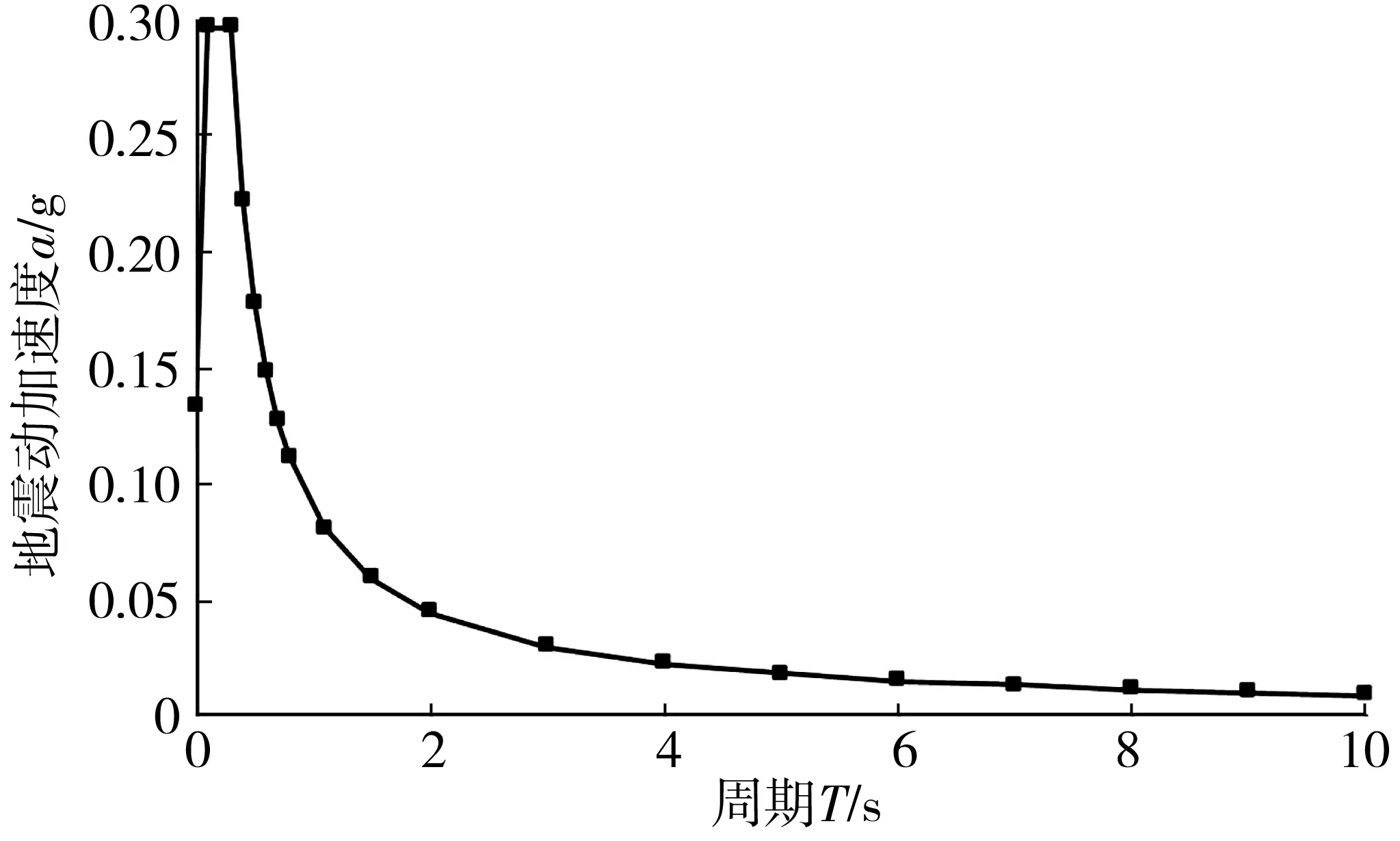
图3 E2地震动设计加速度反应谱曲线Fig. 3 Curve of E2 seismic design acceleration response spectrum

3.2 城口人行悬索桥建模

主缆、吊杆、抗风主索及抗风拉索均采用T3D2杆单元模拟，桥体桁架结构采用B31梁单元模拟，对主缆与抗风拉索分别施加200、150 MPa初始张力。边界约束条件：主缆在索塔处固结，约束X，Y，Z三个方向的线位移和角位移；主索塔根部、风缆主索和主缆采取相同约束边界条件，加劲梁两端约束横向和竖向，另外4个方向自由。城口人行悬索桥三维有限元模型如图4。

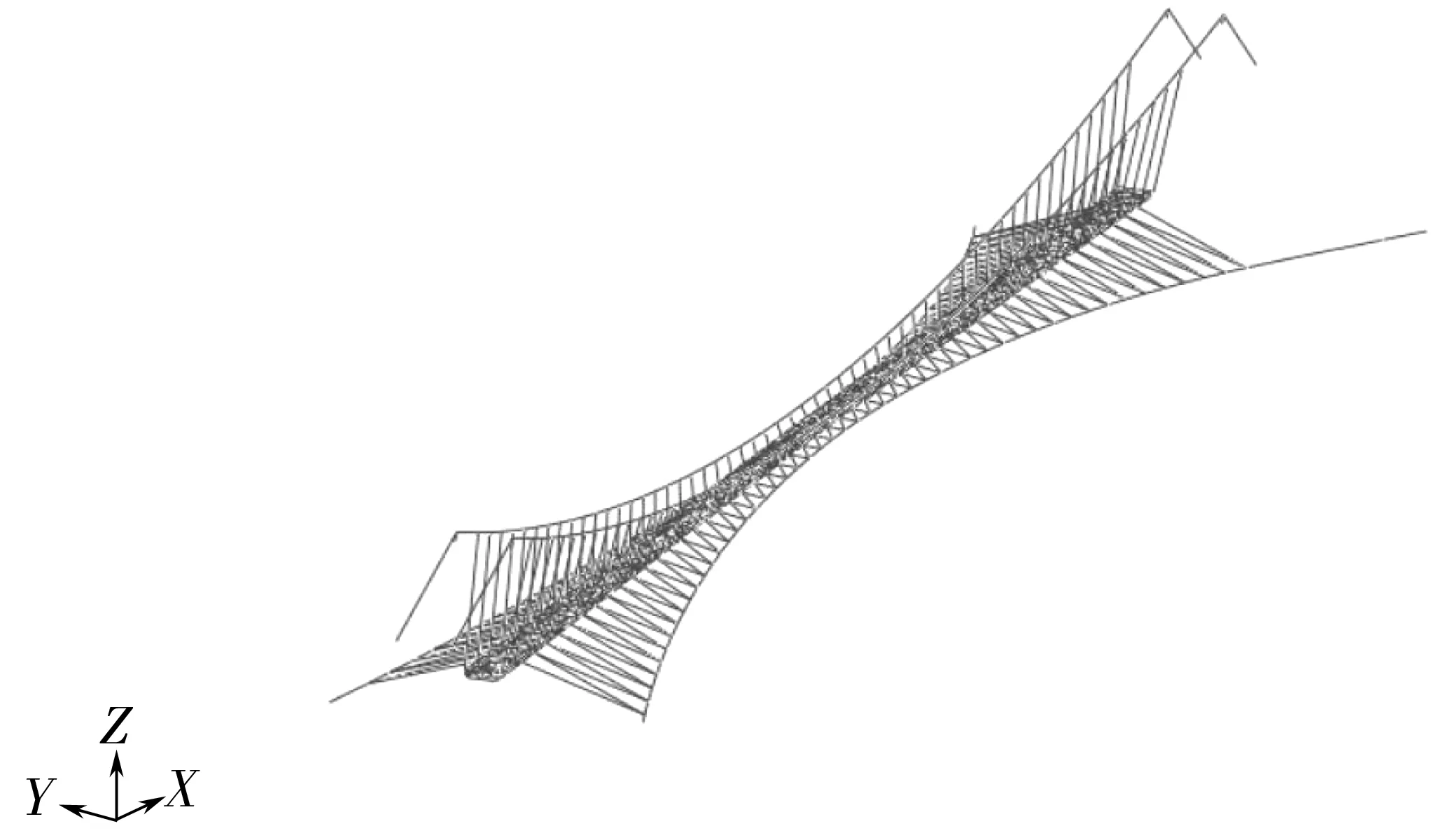
图4 城口人行悬索桥三维有限元模型Fig. 4 3D FEM of Chengkou pedestrian suspension bridge

3.3 城口人行悬索桥反应谱计算

根据对结构动力特性图2的分析，城口人行悬索桥对竖向激励非常敏感，因此，在反应谱计算时仅考虑“纵+竖”及“横+竖”2种工况。E2地震作用下城口人行悬索桥主缆轴力Fcable、主梁弯矩M和位移U如图5。由图5可见，在“纵+竖”及“横+竖”2种工况下：

1)西侧端部吊杆的横向位移较大，如图5(i)、(j)。原因可能是由于端部约束的作用，地震激励下主缆索向下移动，造成西侧端部吊杆承受较大压力所致。可将端部主索换成柔性索或增大端部吊杆初始张力进行改善。

2)主缆最不利位置均发生在东侧端索塔处，如图5(c)、(g)；主梁的最不利位置发生在跨中，如图5(b)、(d)、(f)、(h)。说明地震作用下主缆东侧索塔处与主梁跨中是结构抗震设计的最不利位置，可通过增大抗风索初始张力来提高结构整体刚度，以避免跨中出现最不利内力和位移。

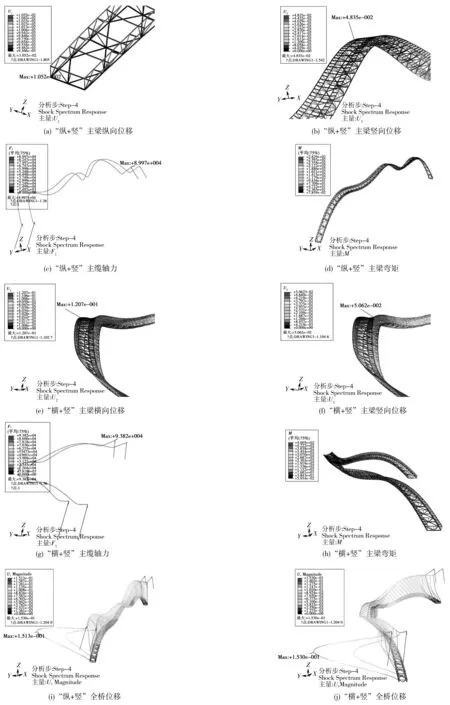
图5 主缆轴力F1、主梁弯矩M和位移U冲击反应谱Fig. 5 Shock spectrum response of main cable axial force F1, main girder bending moment M and displacement U

地震作用下主缆和主梁跨中响应峰值如表3。

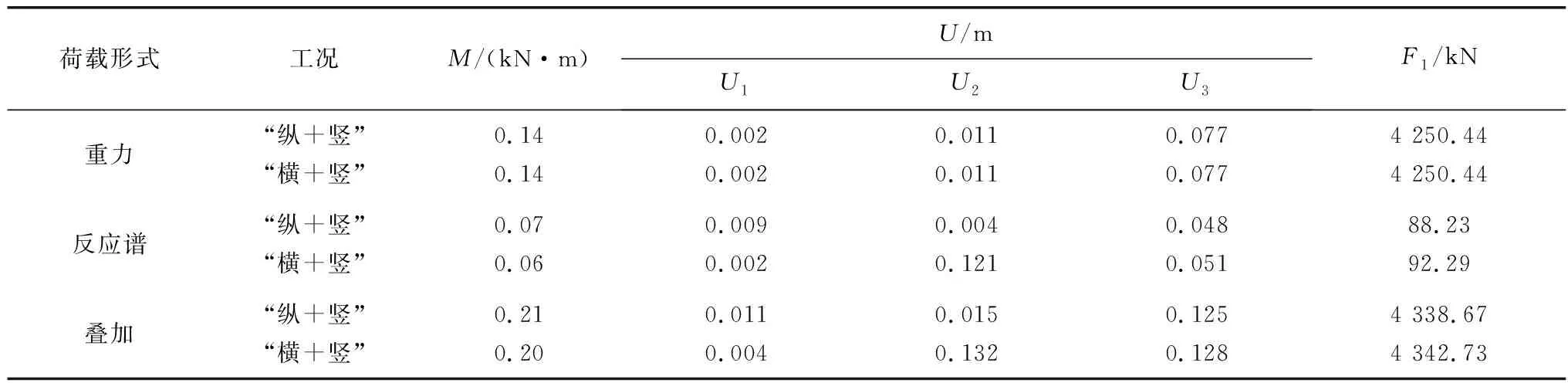
表3 “纵+竖”及“横+竖”地震作用下主缆轴力F1、主梁跨中弯矩M及位移U响应峰值Table 3 Peak values of F1 of main cable, and M and U of main girder under longitudinal-vertical and horizontal-vertical seismic actions

由表3可知：

1)“横+竖”组合地震的内力响应峰值略大，主要激起城口人行悬索桥较大的横向振动和竖向振动；“纵+竖”组合地震内力响应峰值偏小，仅仅引起结构明显的竖向振动，纵向振动不明显。综合分析，“横+竖”组合地震对城口人行悬索桥的影响更大。因此，双向地震作用分析时应重点考虑“横+竖”这种组合地震。

2)城口人行悬索桥结构柔软，在反应谱上又处于长周期范围内，地震激励反应较小，但其自重荷载的反应很大。因此，在输出结构的真实反应峰值时，应将反应谱的计算结果与自重荷载计算的结果相叠加，以叠加的反应谱分析结果与时程分析结果进行对比。

4 一致激励下的动态时程分析

动态时程分析法是分析非线性结构体系普遍适用的方法，其原理是将人工地震波或地震记录作用在结构上，把结构参与振动的整个时间历程划分为微小的时间间隔，对每一段时间间隔按照线性体系来计算。由初始状态开始，逐步对整个时间历程内的地震反应进行积分，从而求出结构在任意时刻的地震反应。这样非线性分析就可近似为一系列线性体系的分析。非线性结构体系振动响应的基础是增量平衡方程[5]：

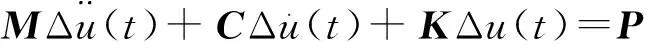
(1)

式中：M、C和K分别为结构的质量矩阵、阻尼矩阵和刚度矩阵；Δu(t)为节点相对于地面的位移增量；P为荷载矩阵。

图6为采用三角级数法[6,7]模拟的人工地震波和拟合反应谱。

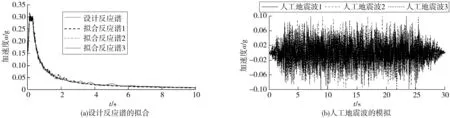
图6 人工地震波与反应谱的拟合Fig. 6 Fitting of artificial seismic waves and response spectra

根据JTG/TB 02-01—2008《公路桥梁抗震设计细则》要求，笔者选用最大的一组地震时程即“人工地震波3”对城口人行悬索桥在E2地震作用下的抗震性能进行分析。地震输入方向为“纵+竖”及“横+竖”双向地震作用下主缆轴力-时程(F1-t)曲线、主梁跨中弯矩-时程(M-t)曲线、及主梁跨中位移-时程(U-t)曲线(纵向位移U1、横向位移U2、竖向位移U3)如图7。

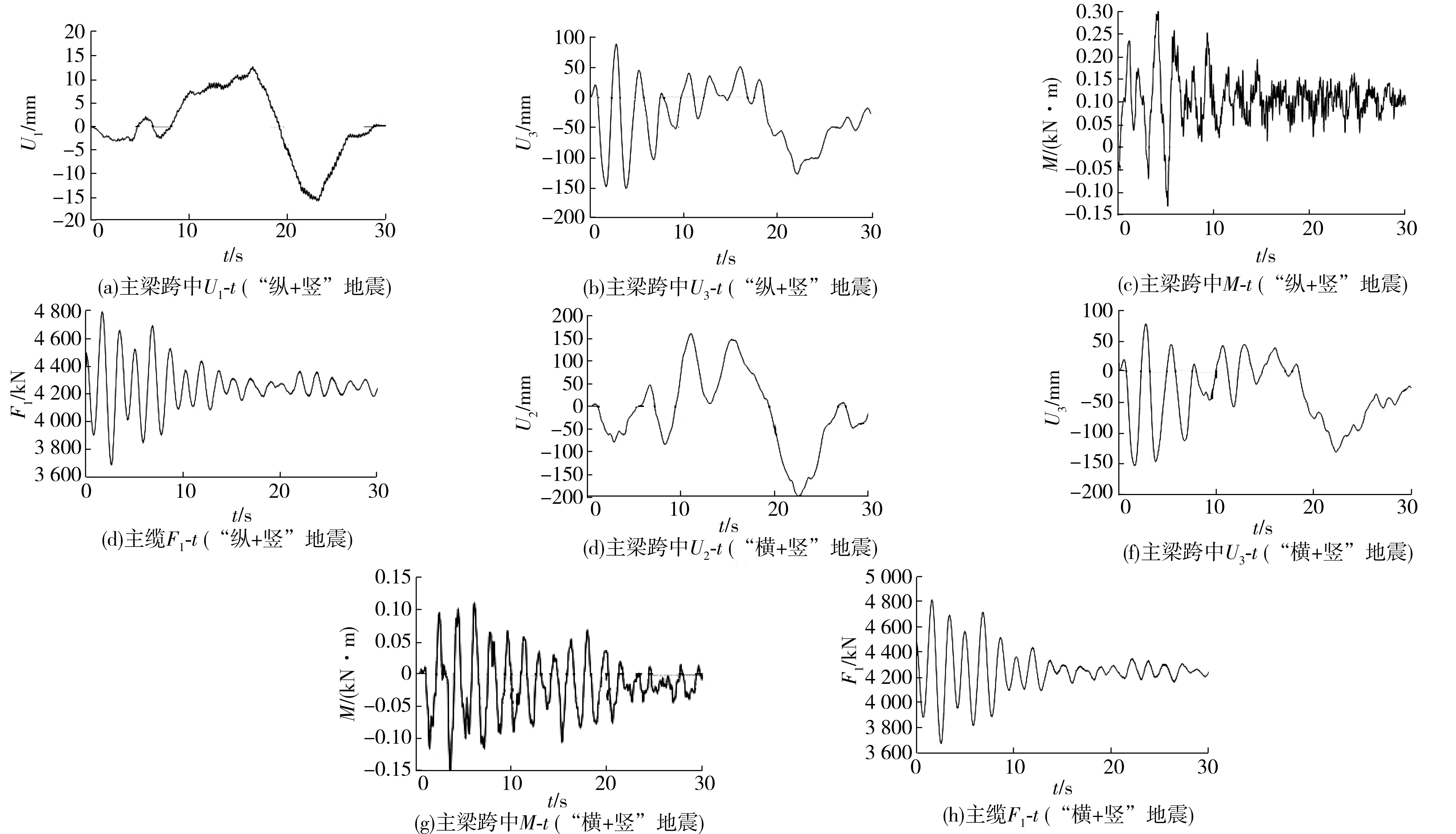
图7 “纵+竖”及“横+竖”地震作用下主缆轴力F1-t、主梁跨中弯矩M-t和位移U-t曲线Fig. 7 Curves of F1-t of main cable, and curves of M-t, U-t of main girder under longitudinal-vertical and horizontal-vertical seismic action

由图7可见：

1)“纵+竖”组合地震作用下，主梁跨中纵向位移大约23 s达到峰值17 mm，竖向位移大约3 s达到峰值160 mm。“横+竖”组合地震下，主梁跨中横向位移和竖向位移在大约23 s分别达到峰值200 mm和16 mm，说明结构主要表现为横向振动和竖向振动，表明城口人行悬索桥对横向激励和竖向激励非常敏感。这与结构动力特性分析中的结论3相同。

2)“横+竖”组合地震内力响应峰值比“纵+竖”组合地震内力响应峰值大，且“横+竖”组合地震的横向位移响应峰值也较大。表明“横+竖”组合地震对城口人行悬索桥的影响更大，这与表3得出的结论是一致的。

采用反应谱分析与时程分析2种方法进行分析，得到主缆及主梁跨中处力学参数响应峰值，如表4。从表4可知：

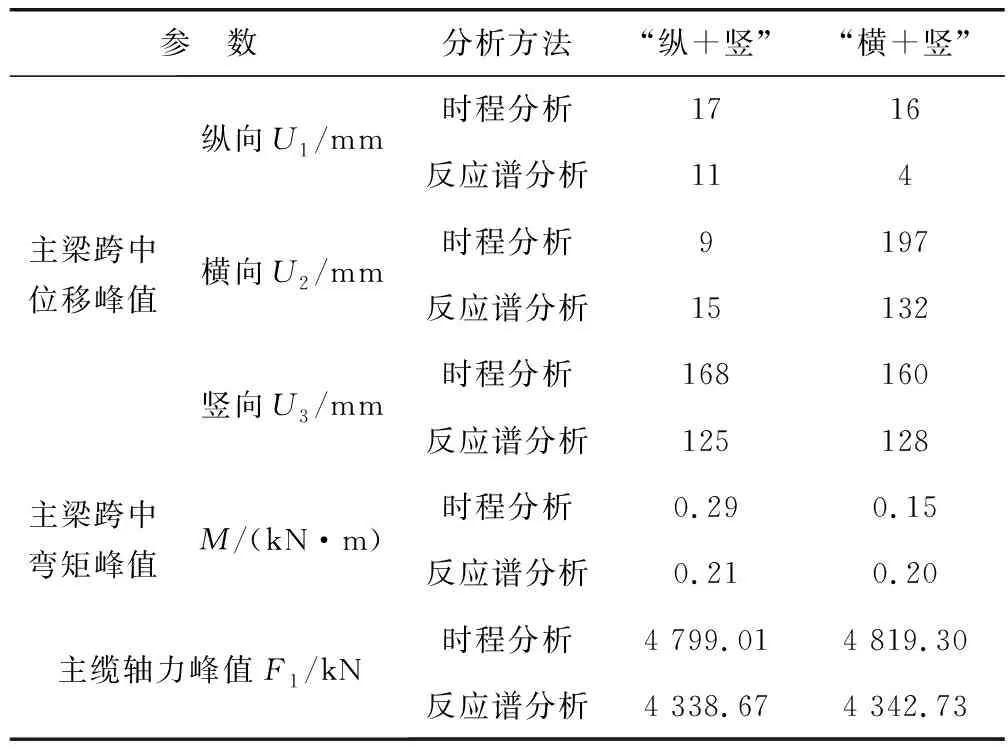
表4 主缆、主梁跨中处力学参数响应峰值Table 4 Response peak values of mechanical parameters of main cable and girder at midspan

1)时程分析结果普遍比反应谱分析结果大，这点与常规悬索桥的规律相反。对城口人行悬索桥这种柔性结构而言，高阶振型的影响显著，高阶振型通常处于反应谱的平台段(高频段)，采用时程分析时在此高频段的地震响应峰值可能就会比反应谱分析的结果要大。

2)对比反应谱分析与时程分析2种方法的分析结果，内力响应峰值吻合较好，位移响应峰值偏差在10%～30%，少数较大，原因可能是单个反应谱与单条人工地震波(影响最大的)进行的计算比较，所以有误差。整体上，2种分析方法的吻合度满足抗震规范要求。

5 结 论

1)城口人行悬索桥整体结构柔软，加劲梁抗扭刚度低，对横向和竖向激励比较敏感。因此，抗震分析时要特别关注这2个方向地震对结构的影响。

2)在“纵+竖”与“横+竖”2种组合地震作用下，主缆最不利位置均出现在东侧端索塔处；主梁的最不利位置均出现在跨中。因此，双向地震分析要重视这2个位置的抗震设计。

3)城口人行悬索桥结构柔性大，在反应谱上又处于长周期范围内，地震作用反应较小，但其自重荷载的反应很大。因此，在输出真实的反应峰值时，应将反应谱的计算结果与自重荷载的计算结果相叠加，否则与时程分析法的校核没有意义。

4)时程分析结果普遍比反应谱分析结果大。2种分析方法的分析结果，内力响应值吻合较好，位移响应峰值偏差大部分在10%～30%，少数较大，吻合度基本上满足抗震规范要求。“纵+竖”与“横+竖”2种地震作用对比，“横+竖”组合地震对城口人行悬索桥的影响比“纵+竖”组合地震要大，因此，抗震分析时要重点关注“横+竖”工况。