考虑大型车因素的城市路网交通流速度预测

闫佳庆，邵 鹏，张立立，王 力

(1. 北方工业大学 电气与控制工程学院，北京 100144； 2. 北京石油化工学院 信息工程学院，北京 102617)

0 引 言

交通流速度预测可以为交通管理和控制提供重要数据基础，是智能交通领域研究的重点和热点。随着机器学习研究的发展，部分学者基于该理论在交通流速度预测领域进行了研究。屈莉等[1]在基于浮动车数据，使用非参数回归方法对路段的交通流速度进行了预测，并将误差反馈考虑到了预测模型中，相对于无反馈的非参数回归法，该方法提升了预测精度；B.YAO等[2]采用了支持向量机(support vector machine, SVM)进行了交通流速度预测，预测模型中考虑了时空特征，相对于人工神经网络和K近邻模型有着较好的预测效果;J.WANG等[3]提出了一种基于循环卷积神经网络 (recurrent convolutional neural networks, RCNN)的时空特征预测方法，在时、空维度上分别采用循环神经网络和卷积神经网络处理，两种模型结合预测效果好于两种模型单独使用;王祥雪等[4]采用了长短时记忆 (long short-term memory, LSTM)神经网络进行交通流速度预测，LSTM在处理时序数据方面有着良好的优势，降低了样本的依赖性提升了运算效率。相关研究表明，机器学习方法在交通流速度预测中具有良好的性能，然而大型车对交通流速度有着重要的影响，但上述研究中并未将其作为物理因素考虑到预测模型中。U.AHMED等[5]在分析了大型车辆与跟驰车辆车头间距和车头时距的影响，研究表明大型车辆对道路通行能力存在较大影响;D.NGODUY等[6]分析了大型车辆对跟驰车队速度的影响，研究表明卡车破坏了交通流的稳定性；S.MORIDPOUR等[7]分析了大型车辆对周围交通特征的影响，道路中随着大型车辆比例的增加，会增加小客车的换道频率和交通事故率，使交通流稳定性下降。

综上所述，大型车对交通流速度的稳定性有着较大影响，基于此，有必要将其引入到基于机器学习的预测模型中，针对路网时空特性对预测时长指数和车辆特征进行分析，并用深度神经网络进行交通流速度预测。

1 研究对象

根据交通流流量和密度基本图可知，以路段流量最大值为界限，将交通流状态分为非拥挤和拥挤两种。拥挤部分作为排队流，非拥挤部分作为行驶流，即二流理论[8]，如图1。笔者将行驶流路段作为研究路段。

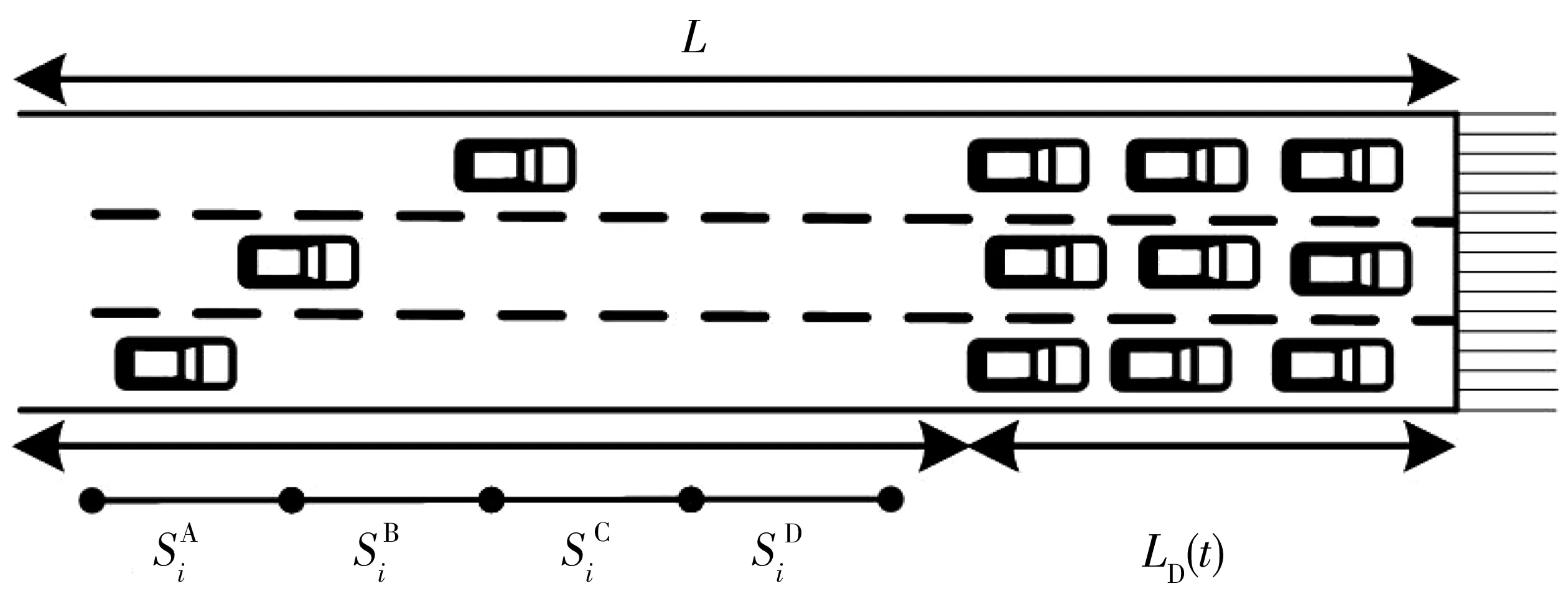
图1 二流理论Fig. 1 Two-fluid theory

路段流量的守恒公式[9]如式(1)：

Nj+Qj,in(t)=Qj,out(t)+Nj(t)

(1)

根据二流理论公式[9]，Nj(t)如式(2)：

Nj(t)=kjLD(t)+km(L-LD(t))

(2)

根据式(1)、(2)，单车道排队长度如式(3)：

(3)

考虑到城市道路的多路段特性，所以扩展公式(3)，得到多车道路段平均当量排队长度模型[9]，如式(4)：

(4)

式中：LD(t)为t时刻上下游路口之间的当量排队长度；Qj,in(t)和Qj,out(t)为t时刻路段上下游路口的流量；Nj(t)为t时刻路段的车辆数；Nj为起始时刻路段的车辆数；L为上下游路口之间的距离；km为上下游路口之间的平均单车道流量最大值对应的密度；kj为上下游路口之间的平均单车道交通流阻塞密度；M为路段单向车道数[9]。

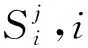
图2 路段单元Fig. 2 Road section unit

2 分析方法

根据路网的时空特性[10]，确定预测时长指数；然后根据大型车特征与路段交通流速度的相关性，引入大型车因素；再建立考虑大型车因素的车辆特征集合；最后根据不同预测时长指数，将车辆的时空特征集合作为GRU神经网络的输入，分别预测目标路段未来时刻的交通流速度。预测时长指数是路网中某路段车辆到达目标路段的旅行时间；目标路段为拟预测的路段。

2.1 预测时长指数

2.1.1 路段相关性

根据到达率计算各路段与目标路段的相关性，到达率定义为到达目标路段的车辆数与各路段中车辆总数的比值，到达率的计算如式(5)：

(5)

式中：Ncar,t为路段到目标路段的车辆数；Ncar,all是路段中车辆总数。依据显著性指标，将不考虑到达率排在5%以下的路段。

2.1.2 预测时长指数确定

根据2.1.1中结果，计算筛选后路段到目标路段的旅行时间。根据短时交通流速度预测经验和考虑到信号控制最大周期原则[11]，不考虑旅行时间在5 min以下的路段。K-Means是经典的聚类算法，它可将旅行时间相近的路段进行聚类，预测时长指数集合C中的各元素为各类的平均旅行时间，见式(6):

C={C1,C2,…,Cm}

(6)

2.2 大型车特征与交通流速度相关性

Cov(X,Y)=E(X-E(X))(Y-E(Y))

(7)

式中：X为目标路段大型车特征时间序列；Y为目标路段交通流速度时间序列；E(X)和E(Y)分别为两时间序列的期望值；Cov(X,Y)>0代表X与Y为正相关关系，Cov(X,Y)<0代表X与Y为负相关关系，Cov(X,Y)=0代表X与Y无相关性。

大型车的车辆数与车辆速度在真实数据采集中较易获得。经协方差公式计算，路段大型车速度时间序列、大型车数量序列与交通流速度时间序列的协方差值分别为0.74和-0.82。协方差在0.5～1和-0.5～-1范围内，可看作对交通流速度有重要影响，因此，作为预测模型的重要输入。

2.3 车辆特征集合建立

车辆特征包括所有种类车辆的平均速度时间序列、小汽车数量的时间序列、大型车数量的时间序列，分别用Vavg(t),Nc(t),Nb(t)表示。根据2.1中路段的聚类结果，km(t)为第m类路段集合，Rlp(t)为路段的车辆特征信息，将车辆的特征集合A(t)作为预测模型的输入，如式(8)-(10)。

A(t)={k1(t),k2(t),…,km(t)}

(8)

km(t)={Rl1(t),Rl2(t),…,Rlp(t)}

(9)

Rlp(t)={Vavg(t),Nc(t),Nb(t)}

对单词进行测试，采用哪种测试形式得根据测试目的选择测试的依据，即测试词汇知识的哪个方面。如果想要调查学习者词汇量的大小或衡量词汇量是否有大量增长，可以考察其接受性词汇（Receptive vocabulary）量的大小。接受性词汇指学习者能认识的、并知道其词意的词汇，即考察学习者是否能根据单词的接受性书写形式（receptive form）知道其词义，这较之考察其他词汇知识更为恰当。

(10)

2.4 交通流速度预测框架

首先进行数据预处理，使用箱线图法进行异常值处理；使用样条拟合方式进行缺失值处理；使用归一化方式进行数据无量纲处理；使用有限冲激响应(finite impulse response, FIR)滤波器进行数据的平滑处理。

笔者选择门限递归单元(gated recurrent unit，GRU)神经网络作为深度学习模型。GRU为发展迅速的一种神经网络[12-13]，该模型相对于RNN模型[14]、BP神经网络模型[15]和ARIMA模型[16]，具有准确性高、鲁棒性强和收敛速度快的优点。基于GRU神经网络的交通流速度预测框架如图3。神经网络框架包括：数据分割、滤波层、输入层、隐藏层、GRU层、输出层；输入层维度包括：车辆平均速度、大型车数量、小型车数量，输出的标签对应为目标路段速度值；数据的训练方式采用小批量梯度下降算法(mini-batch gradient descent，MGD)；时间步长表示利用若干历史输入值预测未来时刻的速度值。

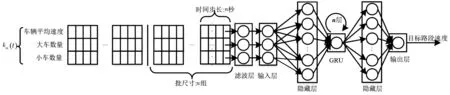
图3 交通流速度预测框架Fig. 3 Traffic flow velocity prediction frame

3 实例分析

实验场景为北京市昌平区部分路网，路网区域内交通较为拥堵，且有着较多公交车线路。根据历史调研数据，建立VISSIM路网仿真，VISSIM路网拓扑如图4。图4中数字为路段标号,有向线段为路段单元。

图4 路网拓扑与分割Fig. 4 Road network topology and segmentation

浮动车数据来源于VISSIM软件仿真数据，假设路网车辆均为浮动车。车辆信息包括车辆编号、种类、速度和位置，依据浮动车最大采样间隔经验，设定采样间隔为3 s，时间为 16:30—17:30，共采集5 d的数据。

根据公式(3)，得到路段排队流平均长度为100 m；经实验证明，当路段单元长度设为100 m时，既能较好表征微观路段的交通流速度特征，又可一定程度上抑制在路段单元之间速度的过度波动。

将路段21作为目标路段，目标路段到达率在5%以下的路段共有12条，分别为29，37，39，36，26，6，14，2，7，40，25，24，这些路段与目标路段的相关性较低，将不作为研究路段。

剩余路段的旅行时间分布聚类如图5，横坐标为路段编号，共有27条路段，纵坐标为各路段到目标路段所有车辆的平均旅行时间。路段3、23、1、31、9、33、15、27、19、34、11、8、5、12、35、13为类别1，路段32、28、38、30为类别2，路段20为类别3。根据各类的平均旅行时间得到了类别1至类别3的平均预测时长，分别为407,619,920 s。由于采样频率较高，末两个路段单元的车辆特征信息可代表整路段的车辆特征信息，作为GRU神经网络的输入，三类路段的车辆特征集合如式 (11)～(15)：

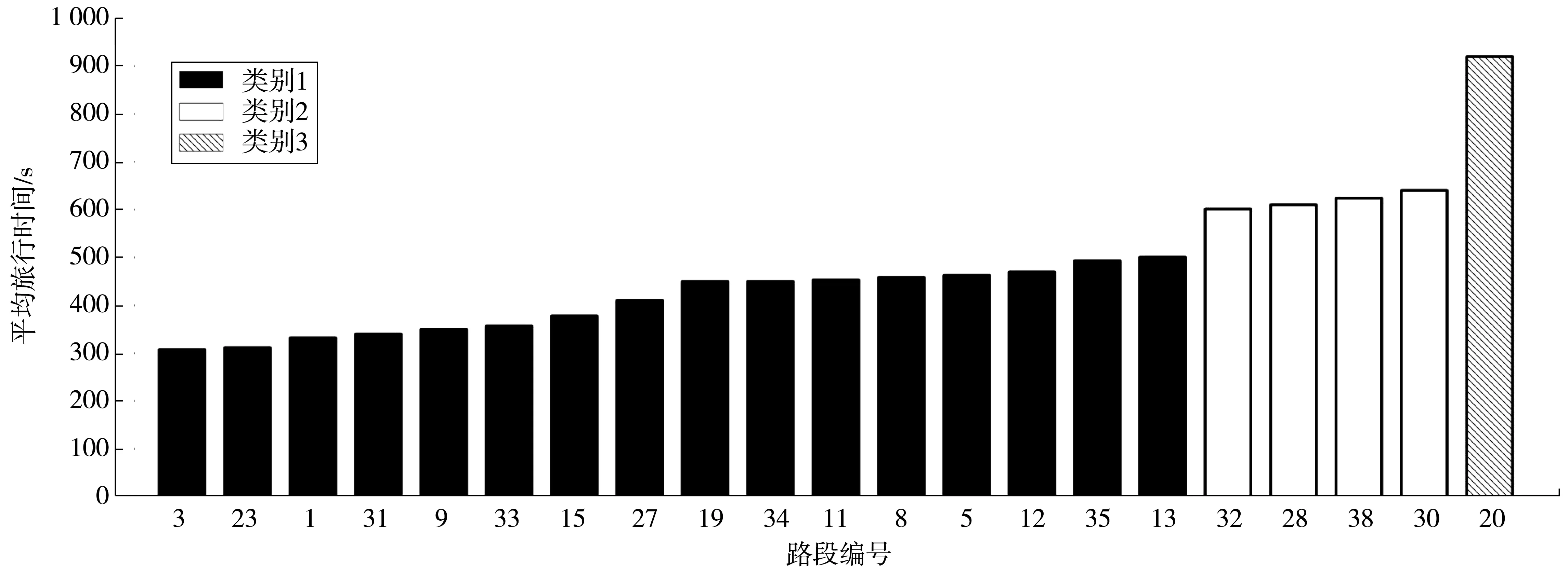
图5 各路段到目标路段的平均旅行时间聚类Fig. 5 The clustering of average travel time from each road section to the target road section

A(t)={k1(t),k2(t),k3(t)}

(11)

k1(t)={Rl3(t),Rl23(t),…,Rl13(t)}

(12)

k2(t)={Rl32(t),Rl28(t),Rl38(t),Rl30(t)}

(13)

k3(t)={Rl20(t)}

(14)

Rl(t)={Vavg(t),Nc(t),Nb(t)}

(15)

通过对GRU进行参数调优[17]，将隐藏层神经元设置为28个，GRU层神经元设置为30个，批尺寸设置为200组，GRU层数设置为8层，时间步长设置为45 s，输入为各类路段的车辆特征信息，训练标签为目标路段对应此类预测时长指数的速度值。前4 d数据作为训练数据，第5 d数据作为测试数据。

以类别1为例，交通流速度预测结果如图6。图6(a)表示预测时长指数为407 s的目标路段预测结果，图6(b)表示38～42 min的预测细节，随着时间的发展，在30 min后，速度值逐渐变小，同时曲线的拟合率有所下降。有无大型车因素的GRU神经网络预测效果对比如表1，评价的指标分别为回归率(R2)、均方根误差(RMSE)和平均百分比误差(MAE)[3-4]，该指标为交通流预测结果评价的常用指标。从实验结果中可以得出，考虑大型车因素的预测结果稳定性与精度优于不考虑大型车因素的预测精度。

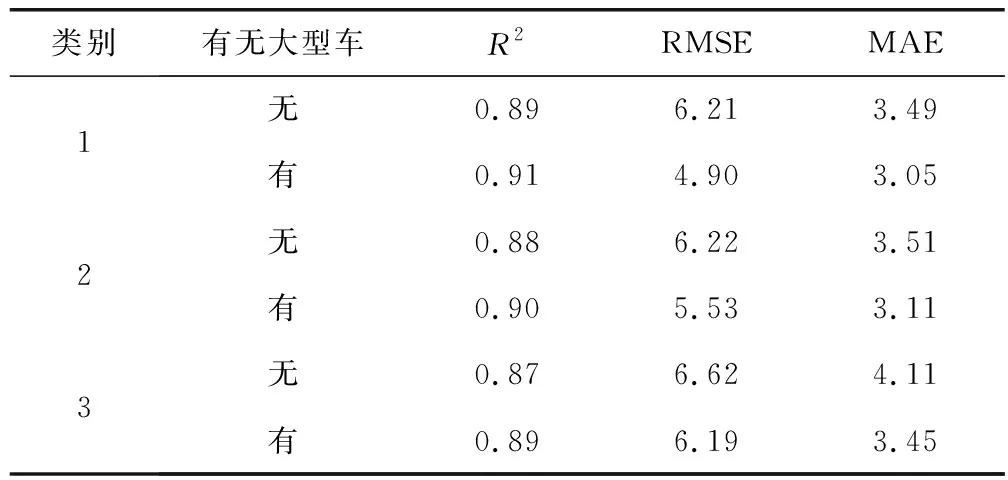
表1 有无大型车预测误差对比Table 1 Prediction error comparison with and without large-scale vehicles

图6 交通流速度预测结果Fig. 6 Traffic flow velocity prediction results

4 结 语

大型车是影响交通流速度的重要因素，针对该问题论文提出了考虑大型车因素的城市路网交通流速度预测方法。首先将行驶流路段作为研究对象，并将其划分为若干路段单元，每个单元包含路段的局部平均速度、大型车数量、小型车数量；然后通过K-Means聚类算法和协方差，分析了预测时长指数和大型车对交通流速度的影响，并将大型车因素引入到预测模型中；最后使用基于GRU的深度神经网络对目标路段进行交通流速度预测。实例分析表明，从类别1至类别3的预测结果可知，大型车因素的引入，使得预测精度提高2%，由此可知本文所提方法具有较好的预测性能。