基于视频的城市道路超车行为影响因素模型
2021-01-18秦雅琴郑号染李剑仕
秦雅琴,郑号染,2,李剑仕
(1. 昆明理工大学 交通工程学院,云南 昆明 650504; 2. 武汉理工大学 交通学院,湖北 武汉 430063)
0 引 言
近年来,机动车拥有量及驾驶人数量迅速增长,人们在享受着机动化程度不断提高带来的便利之外,也承受着随之而来的交通事故频发、拥堵严重等负面效应的影响。相较于高速公路和普通公路,城市道路机动车出行次数更高,发生交通事故的可能性也更大。截至2018年初,我国城市道路总里程占全国道路总里程的7.5%,而城市道路交通事故量及伤亡人数却分别占到全国的45.8%和38.8%,城市道路百公里交通事故率是高速公路的4倍、普通公路的10倍[1]。可见,相较于其他公路,城市道路交通形势更加严峻,相关人员需要加强对城市交通安全问题的重视。在城市道路上,超车行为对交通安全有重要影响,超车不当是造成通行效率低下、甚至导致交通事故的重要因素[2]。关于超车行为的研究,已经引起了相关学者的关注。
国内外相关学者围绕超车现象展开了一系列研究,取得了一定成果。E. I. VLAHOGIANNI等[3]基于贝叶斯网络,构建了超车行为不确定性模型,揭示了超车行为的微观影响因素,并指出男性司机做出超车决策的概率更高;G. HEGEMAN等[4]利用模拟实验检验了超车辅助设备在双车道公路上的效果,发现超车概率与冒险性驾驶行为正相关;J. E. NARANJO等[5]基于仿真分析,设计出了可自主实现路径跟踪及车道变换的超车系统;Z. C. HE等[6]基于最优速度构建了超车期望影响模型;J. X. WANG等[7]基于空间模型,构建了动态和准静态背景下的超车检测模型;H.FARAH等[8]利用模拟实验研究了IGT与超车行为的关系;柏伟等[9]开创性地在将超车过程分为换道、超越、并道3个阶段的基础上,结合车辆跟驰行驶时的安全距离,构建了新型超车判断及辅助模型,并以算例验证了该模型的实用性;单晓峰等[10]通过分析双车道公路超车行为两难区,发现两难区出现的概率随着交通量及车速的增加而增加;陈小龙[11]基于交通流理论及概率论,构建了山区双车道公路超车模型;朱秀娟[12]基于模拟实验得到了双车道公路超车行为安全评价模型。
研究表明,超车行为受多种因素影响,是影响道路安全及通行能力的重要因素。但是,目前此方面的研究主要集中在双车道公路上,关于城市多车道公路超车行为的研究较为匮乏。而城市道路超车行为发生的概率更高,安全形势也更严峻。2018年1月7日,中共中央办公厅、国务院办公厅印发了《关于推进城市安全发展的意见》,交通安全是城市安全的重要组成部分,而工作日和非工作日的交通差异及工作日高峰时段集中出行是城市交通的显著特点。笔者利用视频检测法,开创性地从城市多车道公路超车特性出发,对工作日、非工作日及工作日高峰时段的超车行为影响因素进行分析,分别构建了各自的超车次率影响因素回归模型;分别对工作日与非工作日、工作日与其高峰时段的超车次率模型进行了对比分析,进一步充实了超车行为的相关研究,对推进交通安全管理、强化城市安全基础、提高城市交通安全性有重大现实意义。
1 超车特性评价指标
1.1 超车判定标准
超车是解决车速差异较大的重要手段,但同时也是导致交通事故的关键风险因素[13]。笔者在K. TIAPRASERT等[14]研究的基础上,以车辆通过指定点的顺序变化判定其是否超车。
以x1、x2分别表示上下游断面,定义n辆车为研究对象(n=1,2,3,…,N),t(n,x1)、z(n,x1)表示车辆n通过x1的时间和顺序,t(n,x2)、z(n,x2)表示车辆n通过x2的时间和顺序。以车辆通过上下游的顺序变化判定其是否超车,判定方法如下:
1)当z(n,x1)>z(n,x2),超车数大于被超车数,序号减小(存在只超车的情况,被超车数为0)。
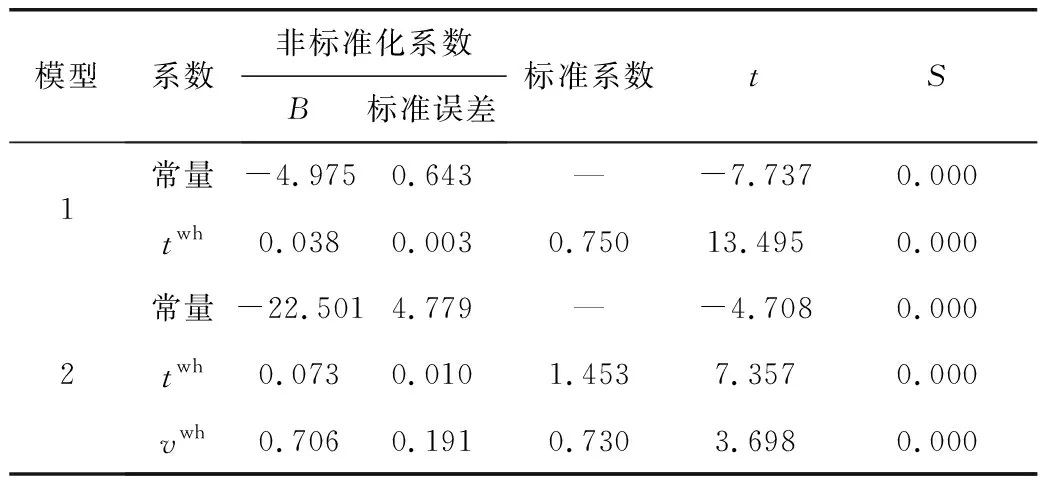
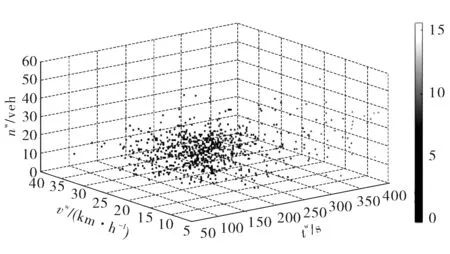
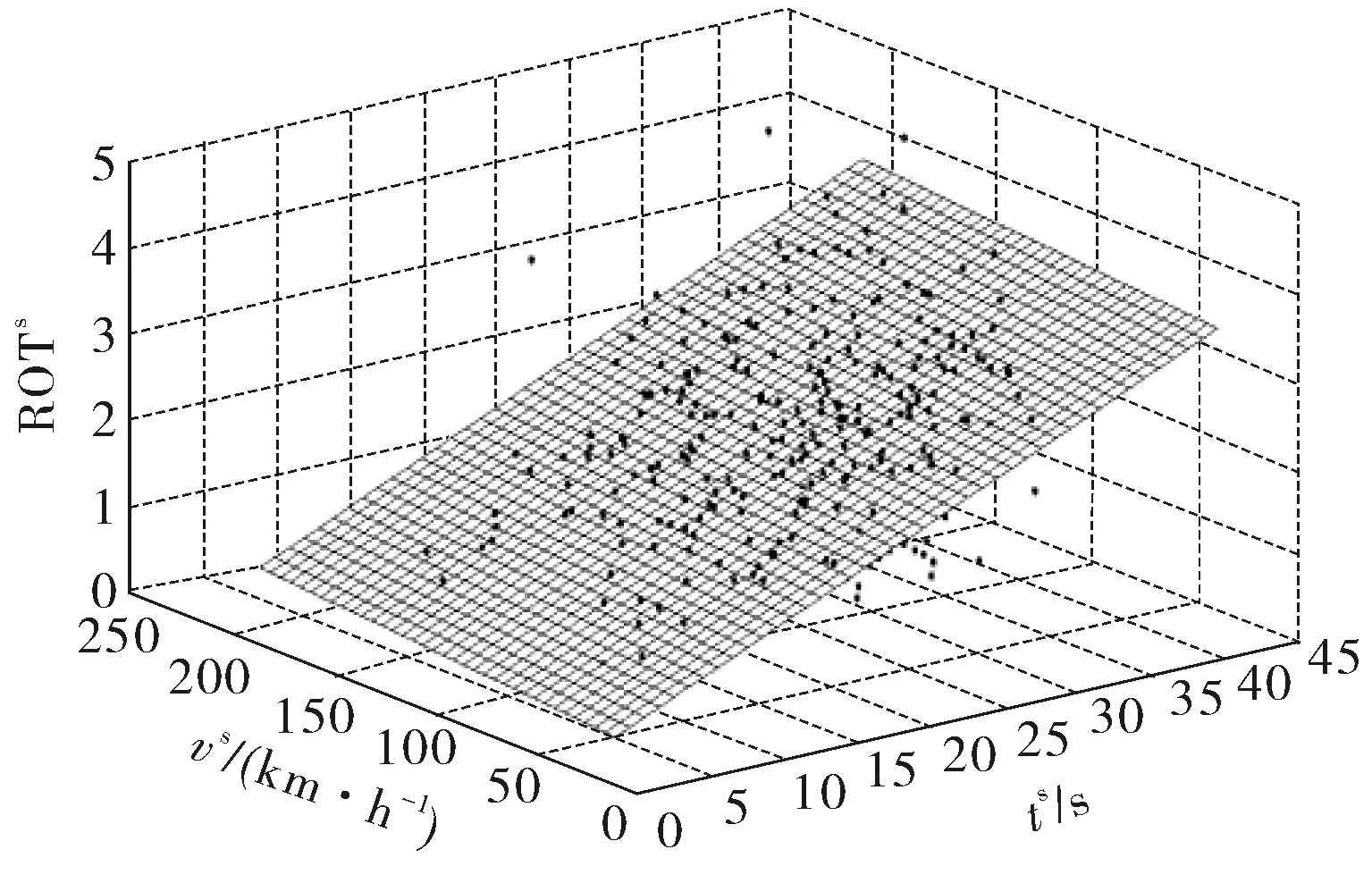
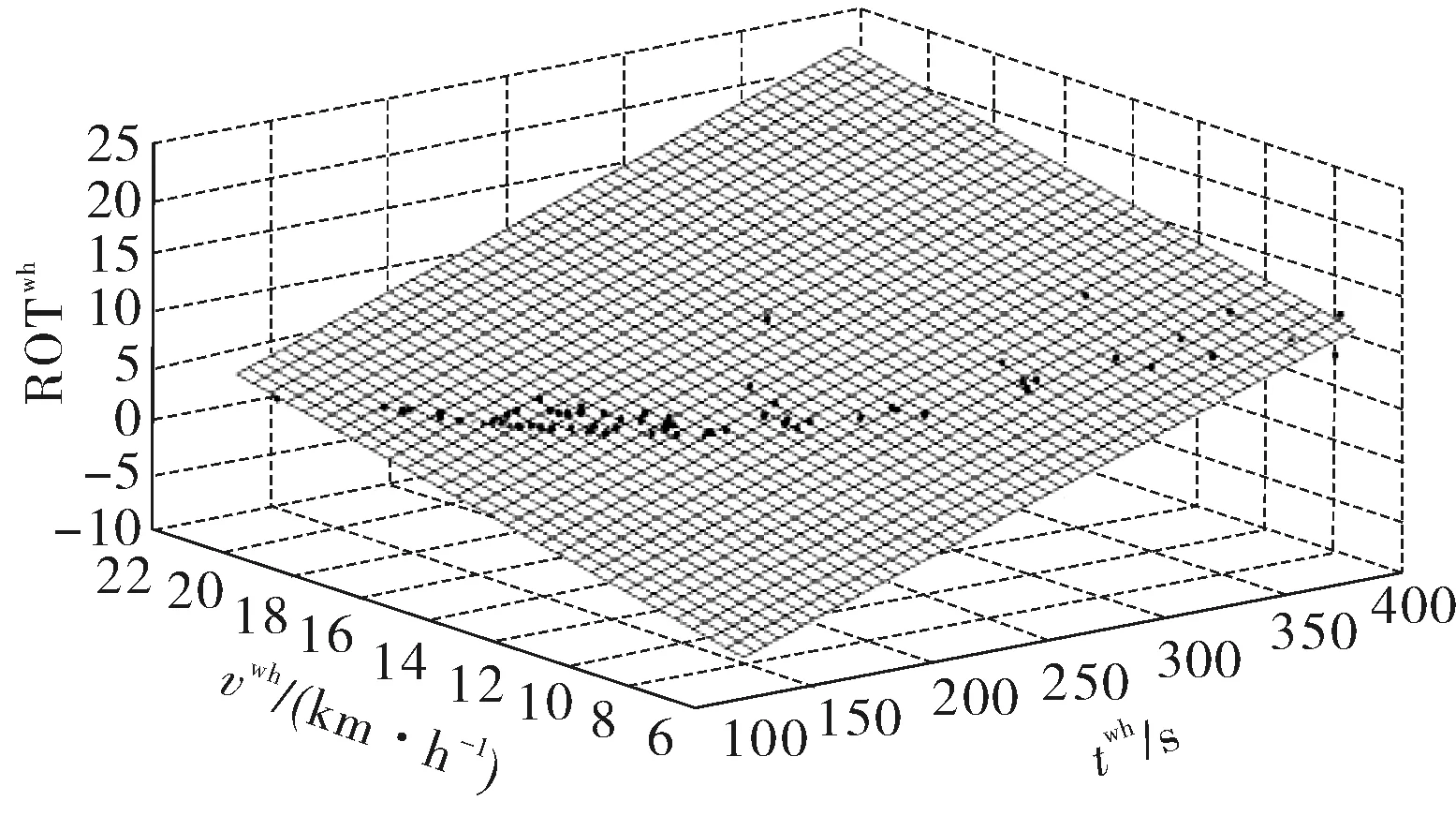
2)当z(n,x1) 3)当z(n,x1)=z(n,x2),有两种情况:①所有车辆均未超车;②超车数与被超车数相等。 超车次率ROT(rate of overtaking vehicle times)表示某时段内路段上超车总次数与全部车辆数的比值,是评价超车现象的绝对性指标,如式(1): (1) 在车辆数为n的车队中,若所有车辆均按“先入先出”规则行驶,则未发生超车行为,ROT=0;若所有车辆均按“先入后出”规则行驶,则ROT达到最大值(n-1)/2。即,ROT取值范围为[0,(n-1)/2]。 数据采集点为秦皇岛市的两个交叉口(分别为采集点1、2)。两采集点间路段单向直行车道数为3,左右转车道数均为1,车辆驶经该路段,两采集点均记录同一车辆的车牌信息,从而得到各车的通过时刻及顺序。设备布置如图1。 图1 视频检测布置Fig. 1 Layout of video detection equipment 2.2.1 预处理 视频设备全天检测,得到海量数据。此外,通信故障、环境因素等均将影响数据质量,因此,需进行数据预处理。 数据质量问题主要包括无效和冗余数据两类:①无效数据主要是由于车辆跟车过近或不按规定车道行驶造成系统无法识别车牌信息,导致回传数据无法与上下游检测点车辆信息进行匹配,进而无法确定车辆的轨迹及其它信息;②冗余数据主要是指同一辆车在极短的时间内先后被摄像机记录两次,并且不在同一车道,此种重复数据将造成部分车辆信息的重叠,不利于数据存储及相关处理。 除数据质量问题外,原始数据中的时间格式为日期时间型,不利于后续时间加减的直接运算。因此,需将日期时间型数据格式转换为类数值型数据格式(Unix时间戳格式:从格林威治时间起至现在的总秒数)。 因此,数据预处理过程涉及到删除无效数据、数据格式转换和删除冗余数据3方面,结合MYSQL与VBA进行数据预处理。预处理后,采集点1、2有效数据分别为216 735条、173 905条。 2.2.2 分周期统计 如图2,车辆运行受信号灯控制,灯态转换前后车辆出发时间差明显增大,故基于预处理结果,对数据进行分周期统计,匹配上下游数据并判断顺序变化,得到各周期超车数据,步骤如下: 图2 灯态转换示意Fig. 2 Schematic diagram of signal light conversion 步骤1:人工确定某周期绿灯始亮时刻t1。 步骤2:t1加上周期间隔值(受车辆性能、司机反应时间等影响,各周期间隔值存在小幅度波动,故以周期时长为标准周期间隔值)得到下一周期绿灯始亮时刻t2。 步骤3:以t2为新的绿灯始亮时刻,进行步骤2的计算。 步骤4:利用VBA依次循环,完成数据分周期统计。 超车行为受车辆数、速度、行程时间、驾驶员素质等多种因素影响[15]。笔者基于视频数据特征,从交通流特性角度考察超车次率影响因素,如表1(上标s、w、wh用于区分非工作日、工作日及其高峰时段的交通参数)。 表1 超车次率影响因素Table 1 Influence factors of ROT 为表征各种因素对超车行为的影响程度,采用回归分析法构建模型。设y为因变量,x1,x2,…xk为自变量,当自变量与因变量线性相关时,模型为: y=b0+b1x1+b2x2+…+bkxk+e (2) 式中:b0为常数项;bi为xi(1≤i≤k)对y的偏回归系数;y为因变量;x1,x2,…xk为k个自变量;e为随机误差。因变量为超车次率,自变量为影响因素,对于n个周期的样本数据,式(2)的矩阵形式为: y=Xb+e (3) 采用多元线性逐步回归得最优方程。回归过程中,每一步均计算已引入变量的偏回归平方和,选取偏回归平方和最小的变量,在给定的F水平下作显著性检验,然后按偏回归平方和递增的顺序依次对其它变量作F检验,仅保留对y影响显著的变量。接着分别计算未引人变量的偏回归平方和,对偏回归平方和最大的变量,在给定F水平下作显著性检验,若显著则将该变量引入方程,循环该过程,直到方程中变量均不能剔除而又无新变量时为止。最后保留的均为对y有显著影响的因素。 分别建立工作日、工作日高峰时段及非工作日的超车次率影响因素回归模型。表2~表7为回归结果,图3~图5为数据拟合结果,其中,ROTw、ROTwh、ROTs分别为工作日、工作日高峰时段及非工作日的超车次率。 3.2.1 工作日超车次率 表2、表3为工作日超车次率模型回归结果。表2、表3中:模型1以tv为预测变量;模型2以tw、vw为预测变量;模型3以tw、vw和nw为预测变量。R为相关系数,df为自由度,F为统计量值,S为显著性,B为非标准化回归系数,t为统计检验值。工作日超车次率影响因素模型如式(4): 表2 工作日超车次率模型汇总及方差分析Table 2 Summary and variance analysis of ROT model on workdays 表3 工作日超车次率模型系数Table 3 Coefficients of ROT model on workdays ROTw=-10.852+0.045tw+0.286vw+0.017nw (4) 式中:nw、tw、vw分别为工作日单周期车辆数、平均行程时间及速度。 可见,工作日超车次率与车辆数、速度及行程时间呈正相关,其中,速度对超车次率的影响最大,行程时间次之,车辆数对超车次率的影响最小。 3.2.2 非工作日超车次率 非工作日超车次率影响因素回归结果如表4~表5。表4、表5中:模型1以ns为预测变量;模型2以ns、ts为预测变量。 表4 非工作日超车次率模型汇总及方差分析Table 4 Summary and variance analysis of ROT model on nonworking days 表5 非工作日超车次率模型系数Table 5 Coefficients of ROT model on nonworking days 非工作日超车次率影响因素模型如式(5): ROTs=-0.243+0.076ns+0.002ts (5) 式中:ns、ts分别为非工作日单周期车辆数及平均行程时间。 由式(5)可见,非工作日超车次率与车辆数及行程时间呈正相关,且相较于行程时间,车辆数对超车次率的影响更大。 3.2.3 工作日高峰时段超车次率 表6、表7为工作日高峰时段超车次率回归过程及结果。表6、表7中:模型1以twh为预测变量;模型2以twh、vwh为预测变量。模型如式(6): 表6 工作日高峰时段超车次率模型汇总及方差分析Table 6 Summary and variance analysis of ROT model in the peak hours of workdays 表7 工作日高峰时段超车次率模型系数Table 7 Coefficients of ROT model in the peak hours of workdays ROTwh=-22.501+0.073twh+0.706vwh (6) 式中:twh、vwh分别为工作日高峰时段单周期平均行程时间及速度。由式(6)可知,工作日高峰时段超车次率与行程时间及速度均呈正相关,且相较于行程时间,速度对超车次率的影响更大。 3.2.4 数据拟合 基于回归结果,得工作日、非工作日及工作日高峰时段数据拟合结果如图3~图5。 图3 工作日超车次率与主要影响因素之间的关系Fig. 3 Relationship between ROT and main influencing factors of working days 图4 非工作日超车次率与主要影响因素之间的关系Fig. 4 Relationship between ROT and main influencing factors of nonworking days 图5 工作日高峰时段超车次率与主要影响因素之间的关系Fig. 5 Relationship between ROT and main influencing factors in the peak hours of workdays 对比工作日及其高峰时段超车次率回归模型可知:行程时间及速度均对超车行为有显著影响,并且在高峰时段,超车行为受两者影响的程度更高,这可能与高峰时段人们的出行目的及时间要求相关。但是,车辆数在高峰时段对超车行为的影响并不明显,这可能与高峰时段交通量较大,超车难度系数提高相关。通过对比工作日及非工作日的超车次率回归模型,发现:行程时间及速度在工作日对超车行为的影响更大,而车辆数在非工作日对超车行为的影响更加明显。交通状态过饱和时,无法正常完成超车。鉴于数据覆盖范围有限,笔者所提模型适用于交通状态未达过饱和时的情况。 以往多为基于模拟实验或实车实验对双车道公路上的超车行为展开研究,数据量较小。此外,超车是驾驶人主观意识的反映,受驾驶人心理因素影响很大,实验中被试往往容易采取与平时驾驶习惯不同的措施,对结果影响很大,难以得到客观全面的超车行为参数,影响结果的可靠性。笔者利用视频法,基于正常驾驶状态下的海量数据对城市多车道公路上的超车特性进行分析,结果可靠。基于城市交通特点,开创性地对工作日全天、高峰时段及非工作日的超车行为影响因素进行了定量分析,对不同交通状态下的超车行为进行了更加细致化分析,对改善城市交通环境、促进交通安全具有实际意义。 笔者基于视频车牌识别技术得到海量交通数据,分析了城市多车道公路上超车行为,得出以下结论: 1)结合MYSQL及VBA对海量数据进行了提取与优化,完成了数据分周期统计。 2)以ROT作为超车特性宏观量化指标,得到了不同交通状态下的超车行为参数。 3)对比工作日与非工作日超车次率模型,发现:相较于非工作日,工作日超车次率受速度及行程时间的影响更大,而车辆数在非工作日对超车行为的影响更明显。 4)对比工作日及其高峰时段的超车次率模型,发现:在工作日及高峰时段,行程时间及速度均对超车行为影响显著,并且,在高峰时段,行程时间及速度对超车行为的影响更大。但是,车辆数在高峰时段对超车行为的影响并不明显,这可能与高峰时段内交通量大,超车难度系数高有关。 相应交通管理部门应着重加强对工作日期间(尤其是高峰时段)的车速管控,鼓励市民(尤其是通行距离较远、行程时间较长的出行者)选择公共交通方式出行,在保障通行效率的同时达到对超车次率进行控制的目标,提高交通安全系数。1.2 超车次率ROT
2 数据来源
2.1 数据采集
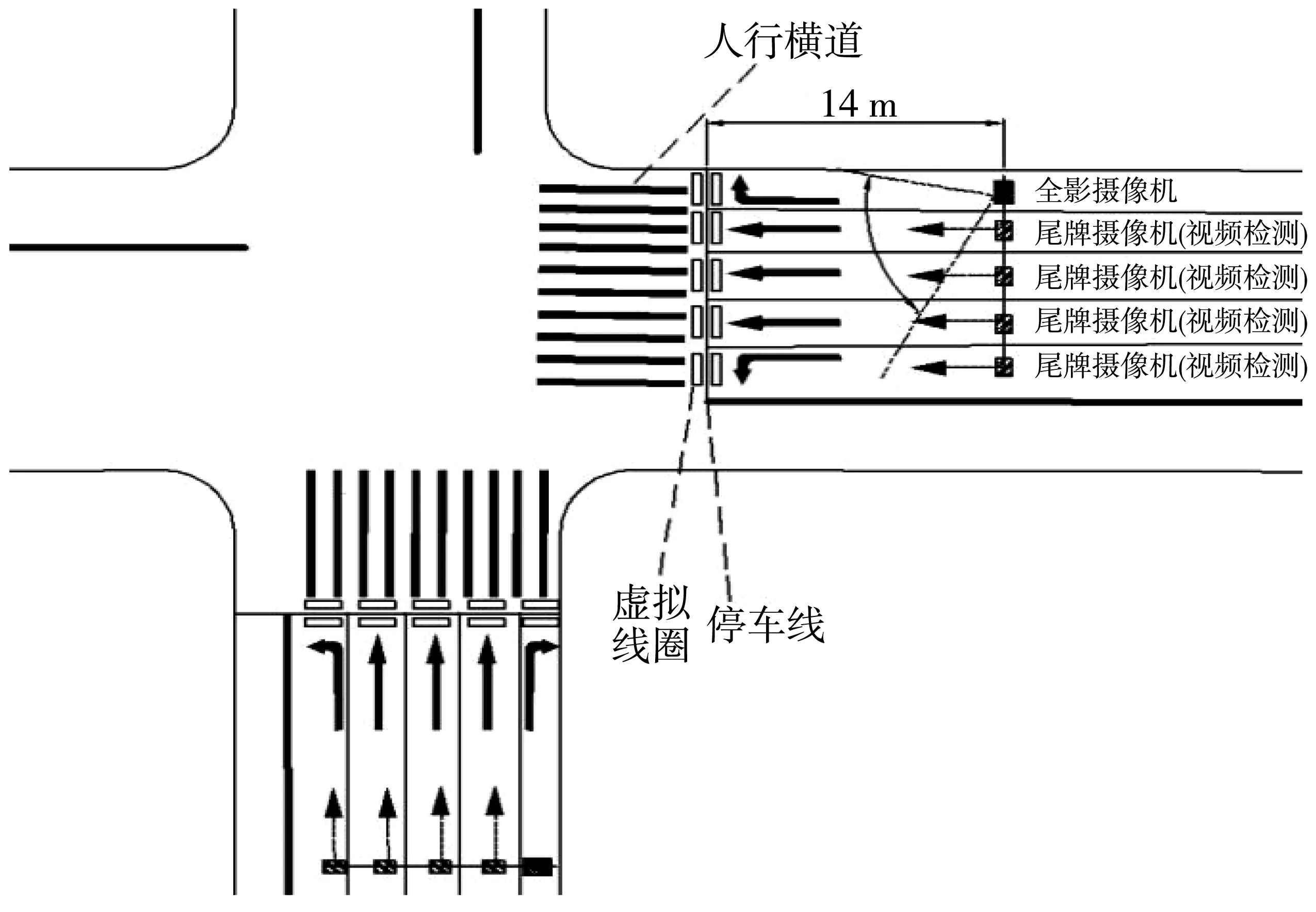
2.2 数据处理
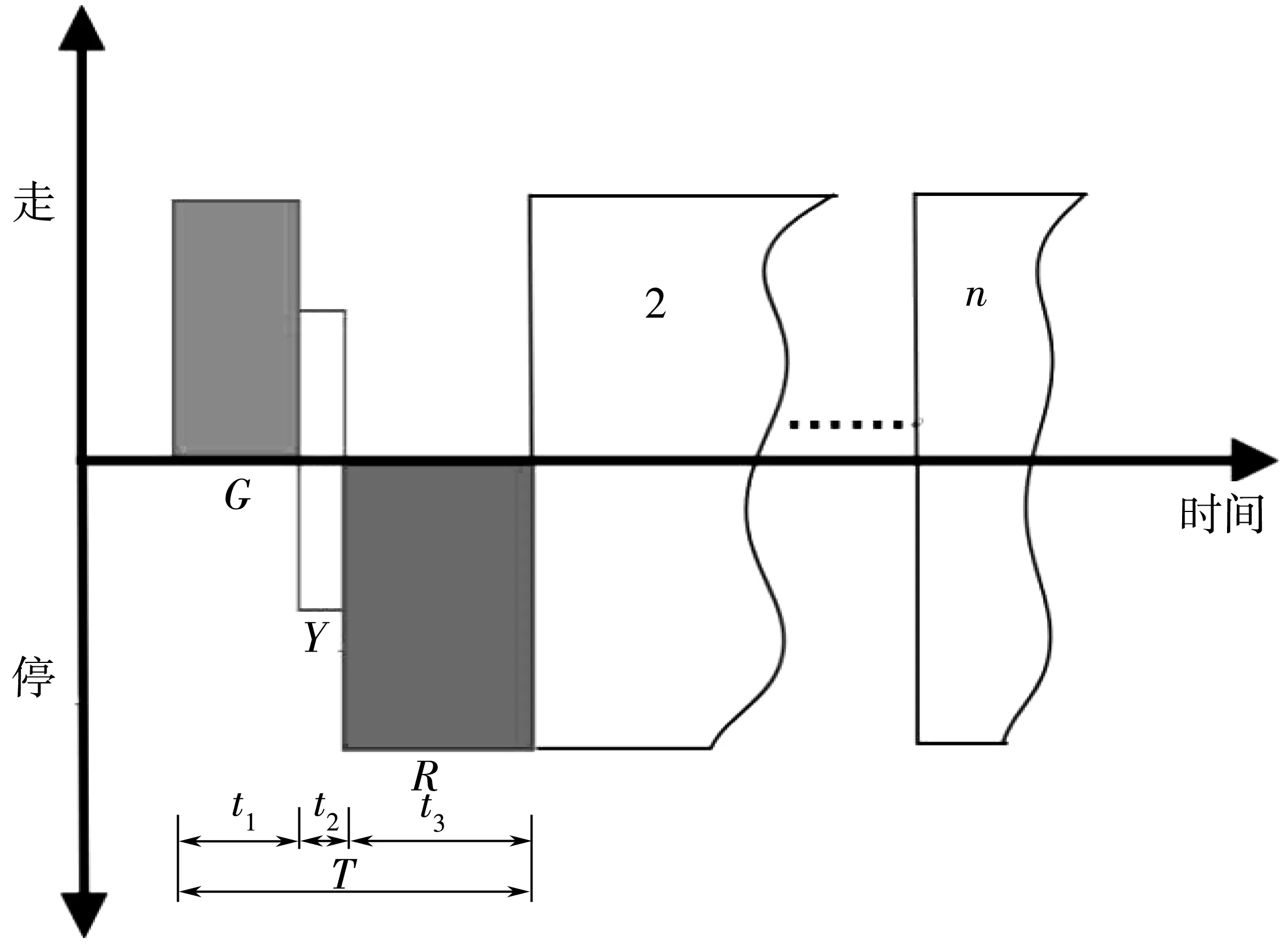
3 超车次率影响因素模型构建
3.1 影响因素

3.2 超车次率影响因素模型
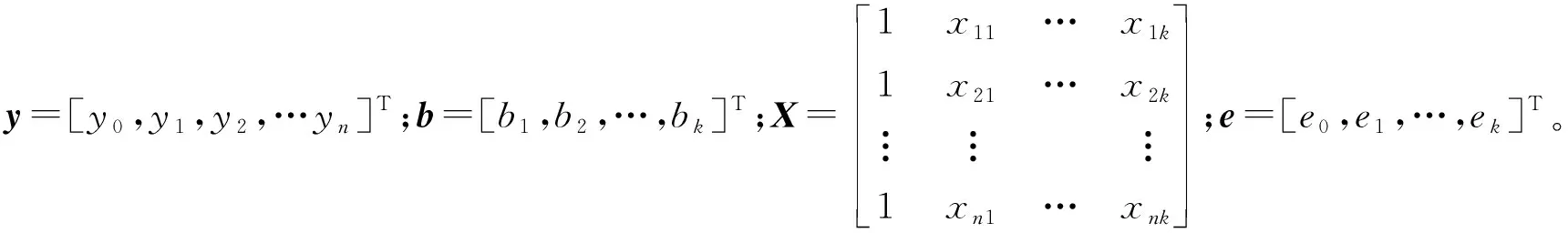
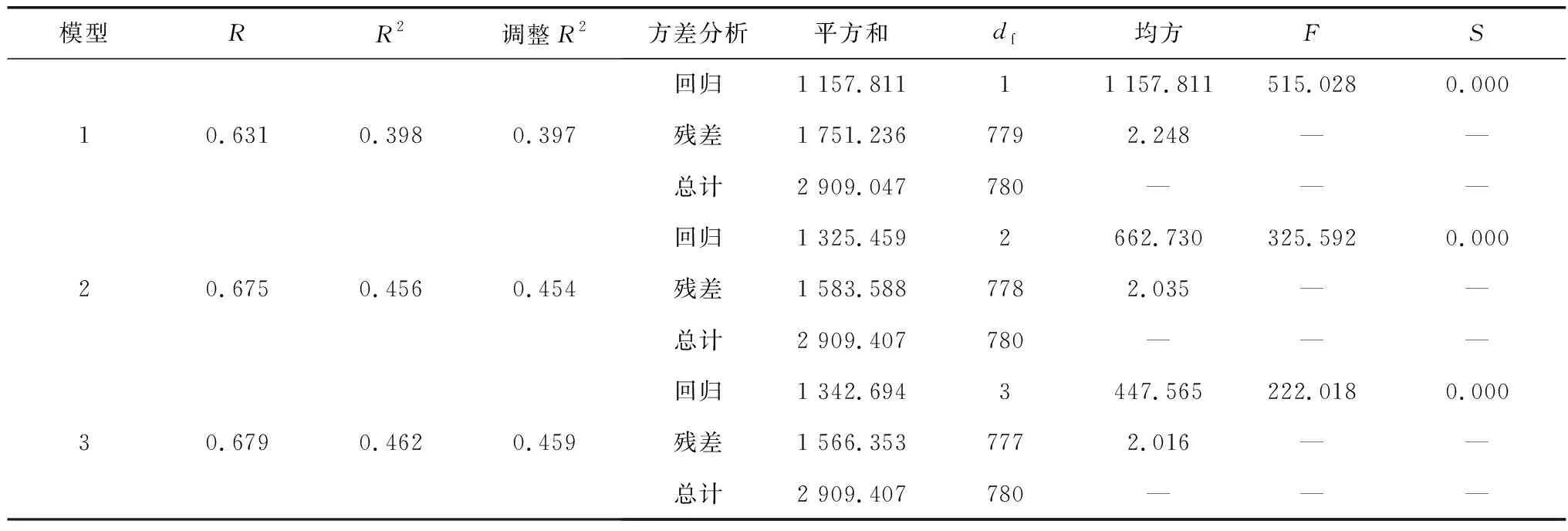
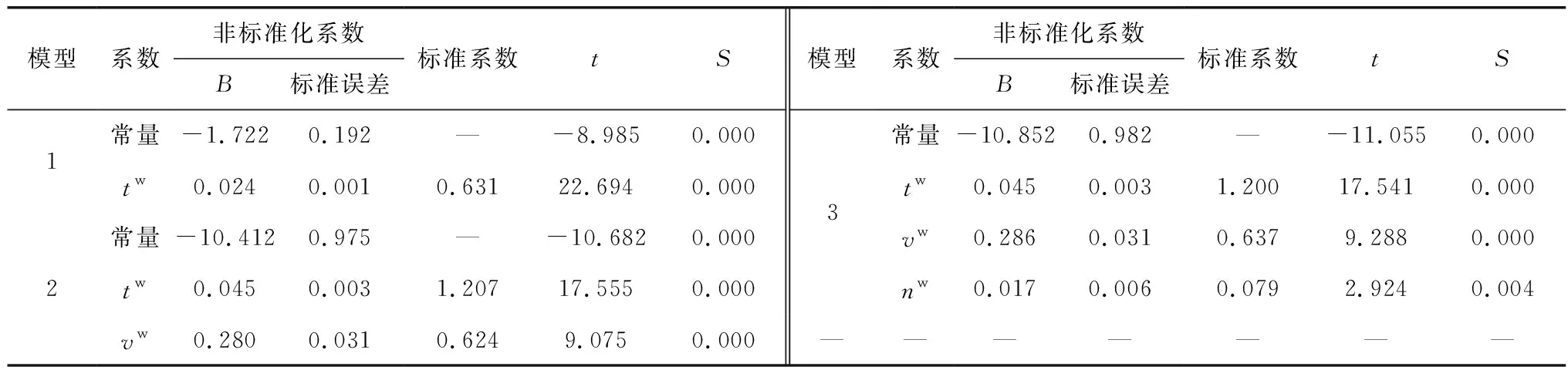
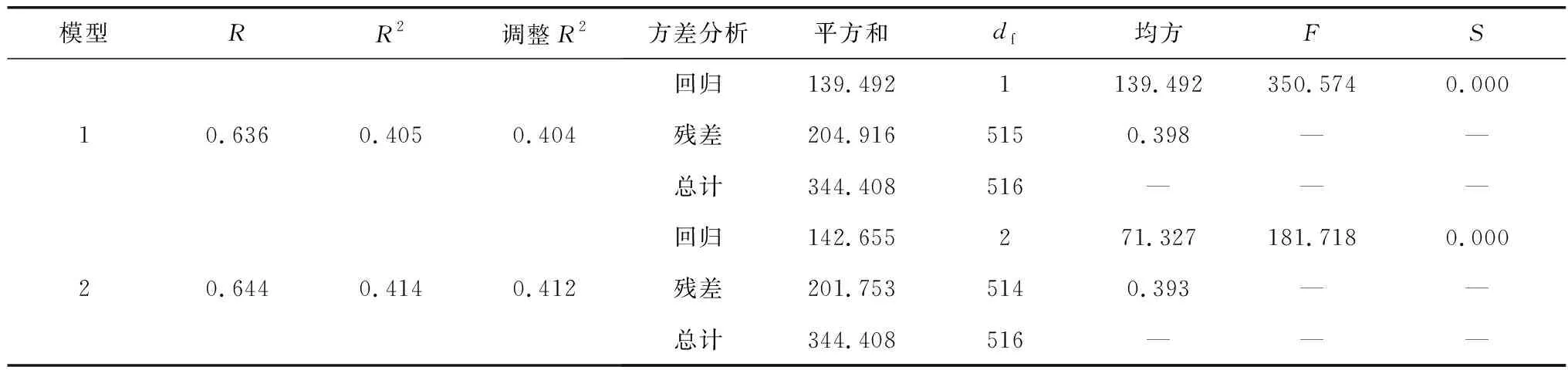
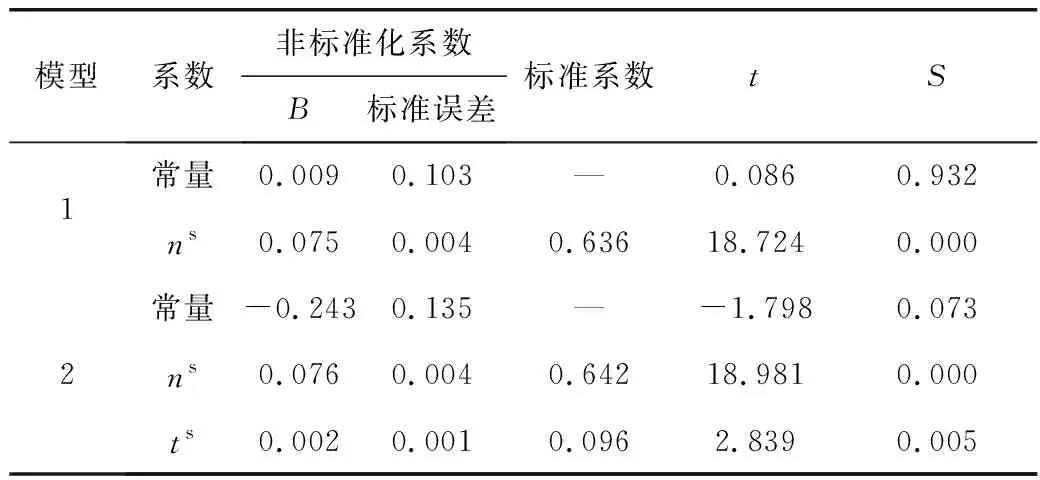
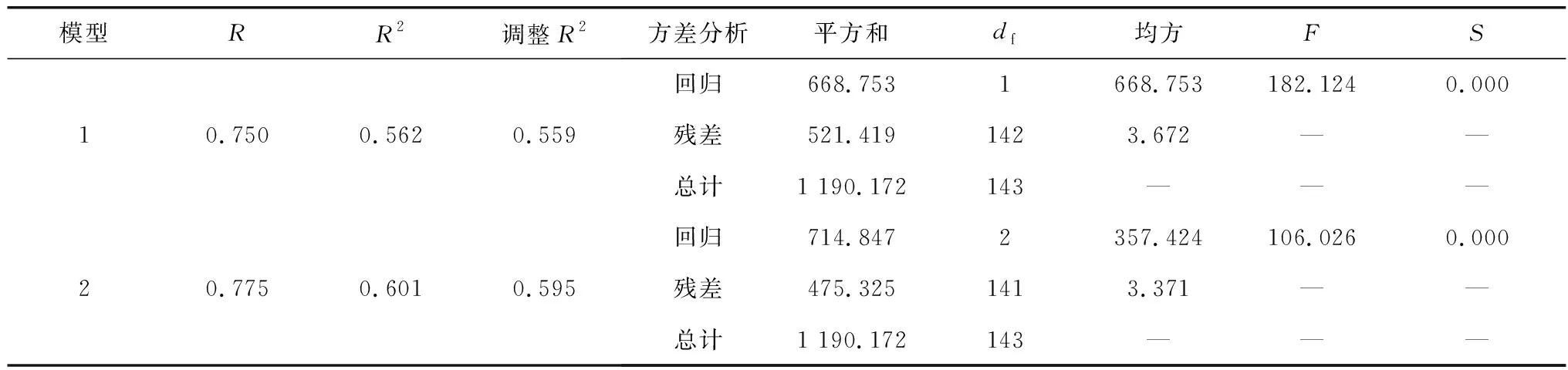
4 结 论
