基于Ring-Barrie相位的交叉口信号配时优化模型

林 丽，蒋帅捷

(南京林业大学 汽车与交通工程学院，江苏 南京 210037)

0 引 言

随着城市规模的扩张，城市居民生活水平的提高，城市内机动车保有量呈上升趋势。同时，人民对交通需求量的日益增强，城市中交通拥堵[1]、滞留问题日益严重。交叉口是一个城市最容易产生交通问题的地方，交叉口信号控制不合理将会导致车辆在交叉口滞留从而导致拥堵。作为整个城市路网通行能力的瓶颈，交叉口运行质量的高低能够直接影响到路网疏解能力的大小。通过针对交叉口实际情况，进行合理的信号配时，来适应不同交叉口不同的车流特点，从而缓解拥堵不失为一种有效的手段。

国内外学者均对信号配时的优化模型进行了大量的研究。如：A. M. ROSHANDEH等[2]选取交叉口内机动车和行人延误为优化目标，建立有关模型以优化交叉口信号配时；张鹏等[3]通过建立判断交叉口各个进口车道的功能划分的数学模型，通过求解模型得到模型中变量周期时长和绿灯时长，以获得优化后控制方案；王逸等[4]选取各相位绿灯时长为优化参数，并采用自适应遗传算法进行求解；张邻等[5]根据周期时长、相位绿信比等特征，建立了周期波动动态信号配时的非线性规划模型；张萌萌等[6]根据各时段的平均流量建立了车辆延误标准差的优化模型，并用遗传算法进行求解。这些信号配时优化模型均针对单环非搭接相位，关于Ring-Barrier相位的优化模型较少。同时，我国交叉口多采用对称相位控制，当交叉口中相对的两个进口车流量不近似时，会明显浪费交叉口的时空资源[7-10]。

以Ring-Barrier相位运行规则为基础，建立了一种基于交叉口平均延误最小的信号配时优化模型；然后采用分支定界法进行此整数非线性规划模型的求解；最后，通过选取以实际交叉口观测车流数据进行实践，并与对称相位和Webster法进行对比分析，验证了文中模型的有效性。

1 Ring-Barrier相位概述

Ring-Barrier相位源于美国国家电气制造商协会(national electronic manufacturers association，NEMA)中提出的交通控制指标，通过为各个车流分别设置控制相位，并互相组合，是一种具有广泛通用性的相位结构[11]。

常见的Ring-Barrier相位控制方案如图1，相位的搭接设置用环(ring)和屏障(barrier)进行描述，环用来描述一系列按照特定顺序执行的冲突相位； 屏障是组织冲突的一种结构。双环搭接相位设置有以下规则：①同一屏障内处于相同环的相位可以同时运行，而处于相同环的相位不能同时运行；②不同屏障内的相位不能同时运行，即使处于不同的环内也不能同时运行，并且同一屏障内不同环的相位运行时间总和必须是相同的[12]。

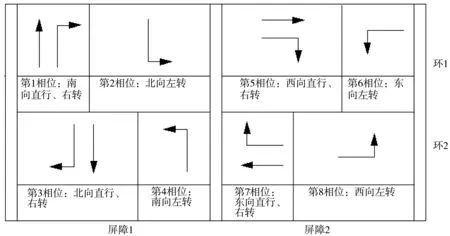
图1 双环搭接相位结构示意Fig. 1 Phase structure scheme of Ring-Barrier

同时，Ring-barrier相位可以有多种相序，拥有多种配时方法，具有一定的灵活性。相较于传统四相位控制方案，Ring-Barrier相位具有更高的车流放行效率，在交叉口管控中有一定的优势。

2 信号配时优化模型建立

评价一个交叉口通行效率的指标一般有通行能力、排队长度、停车次数和延误等。一个交叉口平均延误的大小可以最直观的体现以交叉口的运行效率。

延误指车辆在行驶中，由于受到驾驶人无法控制的或意外的其他车辆的干扰或交通控制设施等的阻碍所损失的时间。笔者选取美国道路通行能力手册(highway capacity manual, HCM)中推荐的公式[13]，由于笔者仅考虑单个交叉口总体延误情况，因此，忽略原公式中由上游信号联动产生的延误。故交叉口中单个车道的平均延误di计算公式为：

(1)

式中：C为信号周期长度，s；ci为车道组通行能力，pcu/h；gei为车道组有效绿灯时间，s；xi为车道组饱和度；t为分析持续时间，一般取0.25；k为感应控制的增量延误修正，定时控制交叉口取0.5；u为上游信号灯车辆增量延误修正，研究对象为独立交叉口取1。

考虑文中研究对象为采用Ring-Barrier的交叉口(图2)，使用1、2、3、4分别表示各个进口道，用L表示左转车道，S表示直行车道，R表示右转车道。

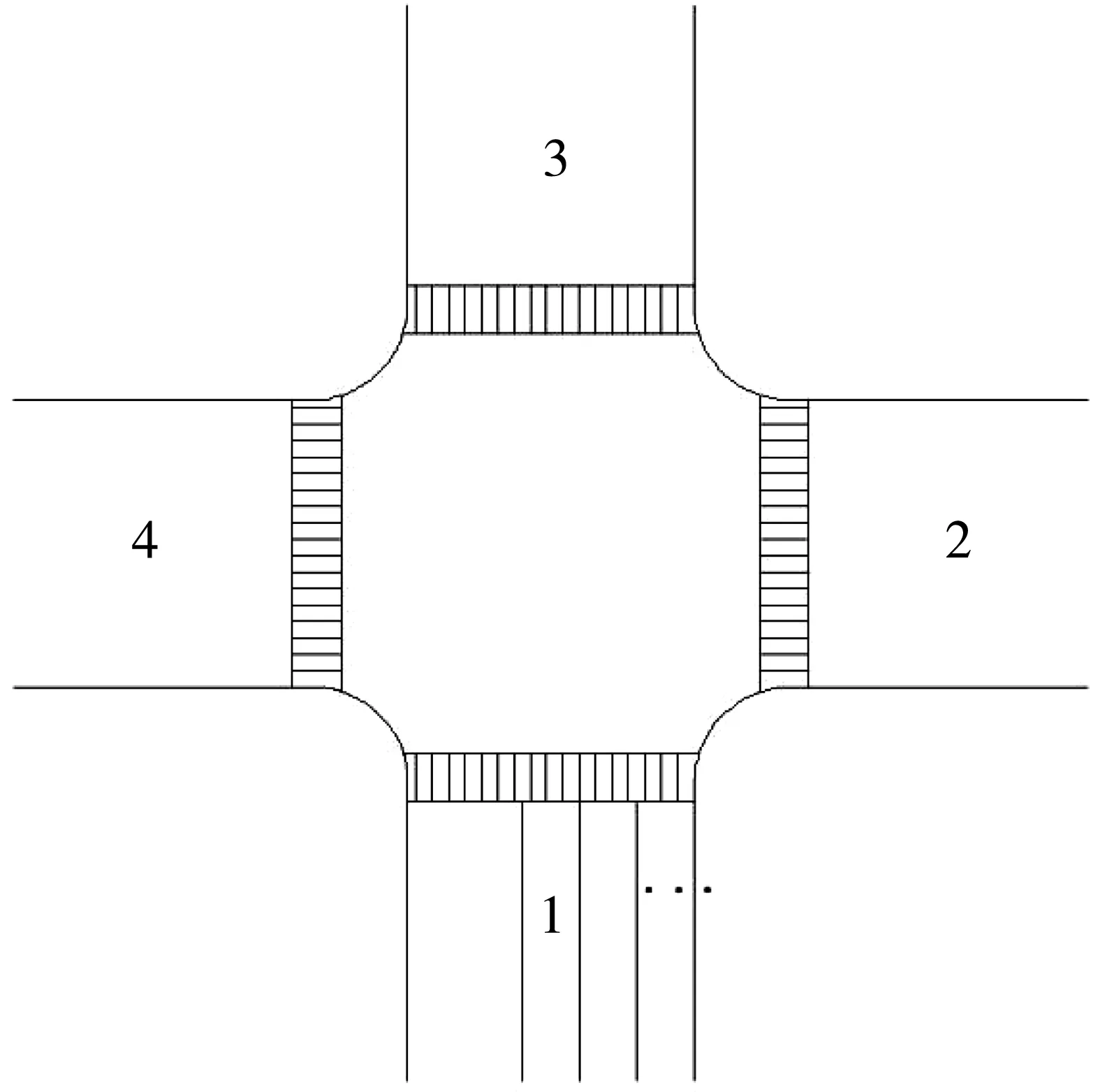
图2 交叉口各进口编号示意Fig. 2 The schematic diagram of each entrance number at the intersection

则交叉口整体延误最小目标函数为：

(2)

式中：qi为各车道流量。

则根据上文所述Ring-Barrier运行规则，各相位绿灯时间满足等式(3)：

(3)

式中：C为信号周期时长。

由于行人随直行车流一起通行，故直行车流绿灯时间须大于等于行人最短过街时间，同时一个相位的绿灯时间不宜过长，以免造成整体信号周期过长[14]，即：

(4)

同时，在交叉口实际应用中，各相位绿灯时间须为正整数[15]，即：

gi∈N*

(5)

式中：Li为i进口直行车流右侧人行横道长度；Vp为行人过街平均速度；I为相位间隔时间。

综上所述，交叉口基于延误最小的Ring-Barrier相位配时优化模型为：

(6)

3 求解模型

上述模型选取交叉口平均延误最小为总体优化函数，并选取各相位绿灯时间作为模型的优化参数，是一个常规的整数非线性规划问题[16-17]。分支定界法作为一种求解整数规划问题的最常用算法，不但可以求解纯整数规划，还可以求解混合整数规划问题。选择分支定界法来进行模型的求解。分支定界法描述如下。

Step1：将上文中建立的非线性规划问题(不考虑整数要求)进行求解，当有最优解时，记此时对应的延误值为Dbottom。

Step2：使用常规Webster法求解各相位绿灯时间，得到延误的值，记为Dtop，若问题的上限值与下限值相等，即Dtop=Dbottom，结束算法，输出各相位绿灯时间对应值；否则，进入Step3。

Step3：在Dbottom对应的各个分支中选择一个不是整数的变量，重新构造约束条件，从而得到两个新分支出来的节点，分别求解两个新分支出的节点(不考虑整数要求)。

Step4：在求解得到的各个节点中，分别选择符合整数要求D的最大值和最小值作为新的Dtop和Dbottom，若此时有Dtop=Dbottom，结束算法，输出各位绿灯时间对应值；否则进入Step5。

Step5：判断各节点的目标函数值，如果有存在大于Dtop，则减掉此分支节点，重复Step3，直到Dtop=Dbottom，即演算停止，并得到此非线性规划问题最优解Dtop。

4 算例分析

Ring-Barrier相位具有一定灵活性，且当交叉口各进口流量不均匀时，使用Ring-Barrier相位配时可以有效减少由于各进口流量不均匀导致的交叉口时空资源的浪费，以达到增加交叉口通行效率的目的。

为验证所建模型的有效性及适用条件的特殊性，选取南京市城区一符合条件的交叉口为例。通过实地调查获取高峰时段(18:00—19:00)1小时交叉口交通量。将车流量转换为标准小汽车当量，各进口车流量如表1。

表1 交叉口各进口流量Table 1 Traffic flow at each entrance of intersection pcu/h

使用上文提出的模型对交叉口信号控制进行优化计算，经过39次求解，得到了最终优化方案。原路口配时方案，Webster法配时方案和新配时方案如表2。

表2 算法优化结果对比Table 2 Comparison of algorithm optimization results

根据表2可知，相比与对称相位，优化方案平均延误减少了10.2 s，减少率为16.5%；相比与Webster Ring-Barrier配时模型，优化方案平均延误减少了21.11 s，减少率为29.1%。由此可见，文中优化模型效果较好。

5 结 论

在Ring-Barrier相位规则的基础上，选取延误最小为优化参数，建立交叉口信号配时的优化模型。并选取一实际交叉口为例，分别使用传统Webster法和Ring-Barrier优化模型分别配时，得出以下结论：

1)相比于传统Webster配时方法，Ring-Barrier相位具有一定的优越性，并有着更高的放行效率，能够有效减少交叉口延误。

2)所提出的基于平均延误最小值的优化模型是一种整数非线性规划模型，可以借助常规工具软件进行求解，易用于实际。