基于轨迹压缩的航空器飞行轨迹聚类研究
2021-01-18强懿耕
李 楠,强懿耕,樊 瑞
(中国民航大学 空中交通管理学院,天津 300300)
0 引 言
近年来随着我国民航业的高速发展,复杂机场已陆续实施基于性能导航(PBN)的导航技术来提高运行和指挥效率,因此需要设计新的PBN程序来简化传统的标准飞行程序。笔者针对飞行密度大、飞行情况比较复杂的终端区空域,通过聚类算法分析航空器历史轨迹,挖掘航空器潜在的飞行模式,其中所蕴含的管制员指挥模式可作为评估、优化进离场程序的重要参考。
轨迹聚类分析是目标轨迹模式挖掘过程中常用的方法,用以探究隐藏在海量轨迹信息中目标的运动特征与规律,在探索人类的移动模式、飓风的运动模式和城市交通结构智能划分等[1-3]诸多领域已经得到了广泛的应用。目前,在航空领域中,国内外学者对航空器飞行轨迹的聚类分析多集中于两个方面。一是借助经典的聚类方法(K-means,FCM等)来分析整条轨迹或轨迹段,挖掘轨迹的运行模式,如C. WANG等[4]针对具体的一类航迹簇,采用基于K-Means算法对航迹相似性矩阵进行聚类分析得到该类簇的中心航迹,计算中心轨迹与标准进场飞行程序(STAR)的偏差来为重新设计飞行程序提供参考;R. FRANK等[5]采用轨迹点比对的方法计算出轨迹间的相似性距离,再针对相似性距离矩阵进行聚类分析;Q. Y. YU等[6]提出了一种基于多特征轨迹相似性度量的新轨迹聚类算法,可以最大化同一聚类轨迹的相似性;A. SALAPOUR等[7]采用时间扭转匹配的方法来度量轨迹间的相似性,提出了一种基于方向的轨迹聚类相似性度量;李楠等[8]建立了基于速度修正系数的轨迹相似性模型,再应用谱聚类实现了航空器飞行轨迹的合理分类;郭威等[9]沿用传统的最小描述长度方法划分轨迹,再结合密度聚类和扫描线算法得出表征目标物体运动的特征轨迹;徐涛等[10]引入惩罚弧形面积改进了在计算轨迹间相似度时轨迹航向的影响,再利用聚类方法准确地挖掘出了飞行程序轨迹。二是通过借助几何模型或其他机器学习算法对轨迹重采样,使重采样后每条轨迹的轨迹点数和维度均保持一致,直接进行聚类分析,避免了使用相似性度量方法计算轨迹间的距离,如赵元棣等[11]在保持较低失真率的前提下使用主成分分析法降低数据维度,再运用均值漂移聚类算法实现飞行轨迹聚类分析并提取出异常轨迹;王涛波等[12]在采用模糊减法聚类提取轨迹特征点后,运用改进后的模糊聚类方法直接对航迹特征点进行聚类并构建相应的中心航迹,更好的反映了真实飞行中航空器的飞行模式。以上研究存在有待改进的地方,仅仅考虑轨迹间的空间距离对航空器进行聚类划分是不够的,时间是影响聚类结果的一个重要因素;由于轨迹点自身包含位置、速度和航向等多维特征,建立相似性模型时可以在考虑位置特征的前提下引入速度和航向等动态特征;当轨迹规模较大且噪声点较多时,常用的聚类算法容易受初始点对噪声敏感、多个参数输入且需要先验知识等因素影响,陷入局部最优搜索,导致聚类效果变差。
1 航空器飞行轨迹数据处理
1.1 航空器飞行基准轨迹
在监视数据库中,航空器飞行轨迹是由离散的数据点依时间顺序连接而成的点序列。采用某机场终端区ADS-B监视数据作为原始数据。考虑到原始轨迹中包含大量不完整轨迹、飞越航班和临近机场起降航班的轨迹,需要进行轨迹预处理。
根据航空器飞行特点筛选出进场航班,删除轨迹点严重缺失的轨迹,采用时间间隔为3 s的线性插值更新剩余轨迹。鉴于ADS-B接收机受地形和传输损耗的影响,导致测量值与真实值存在一定的误差,所以结合CV卡尔曼滤波算法平滑处理轨迹,最大限度地接近飞机的真实位置,建立航空器飞行基准轨迹。
1.2 基于时间比的自顶向下飞行轨迹压缩算法
经线性插值和平滑处理后的轨迹包含大量的轨迹点,采用Top-Down Time Ratio算法压缩轨迹,以减小计算开销,从根本上提高轨迹大数据分析能力。Top-Down Time Ratio算法是Douglas-Pecuker(DP)算法的扩展。与传统DP算法不同的是,DP算法在考虑空间特性的前提下还考虑了时间特性,判断是否为轨迹关键点的依据也由DP算法中的垂直距离变成了同步欧氏距离 (SED)[13]。同步欧氏距离指原始轨迹中真实轨迹点与其在轨迹首尾连接线上按时间比例所求得的欧氏距离。
如图1,A到K为原始轨迹中相邻的轨迹点,具体的轨迹压缩步骤为:
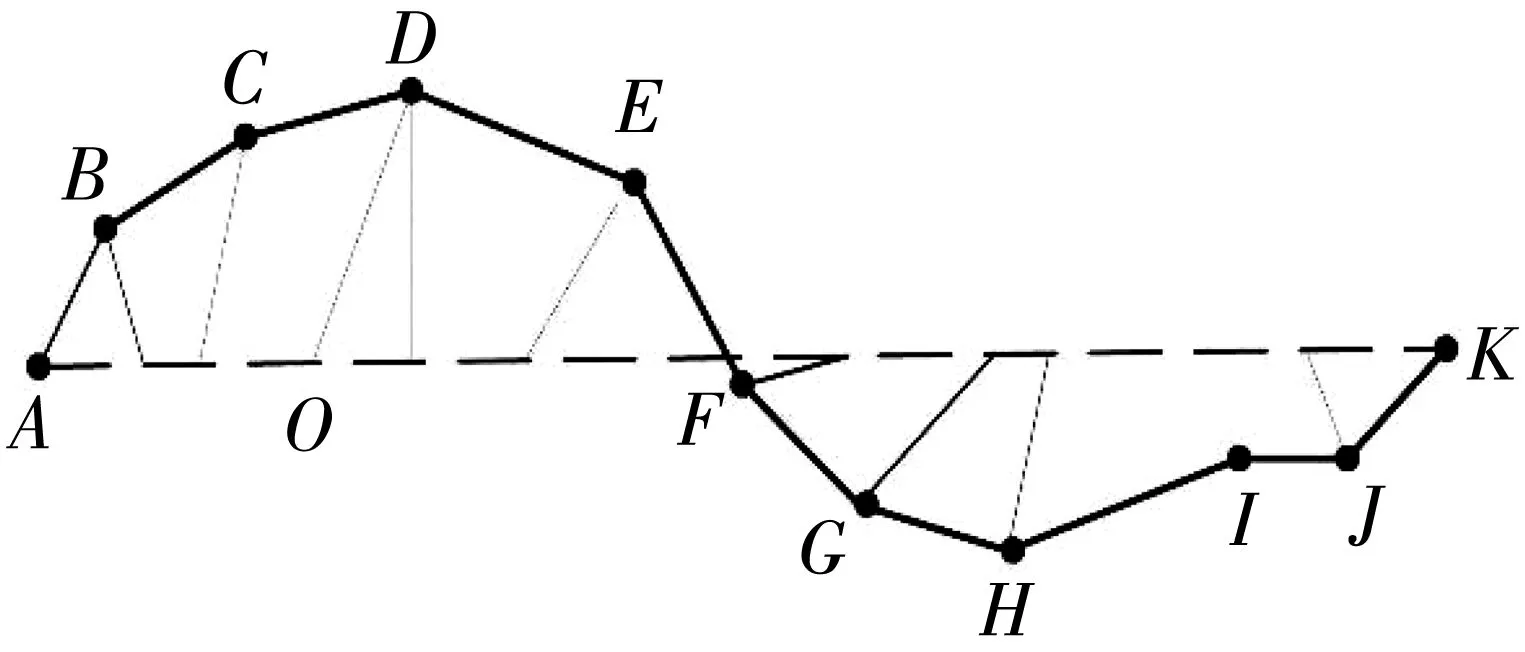
图1 Top-Down Time Ratio轨迹压缩算法Fig. 1 Top-Down Time Ratio trajectory compression algorithm
步骤1:将轨迹首尾两点A,K连接成一条直线,该直线称为轨迹的弦。
步骤2:应用同步欧氏距离(如图1中DO),计算离弦距离最远的点及其距离,比较该轨迹点距离与误差阈值距离D的大小。
步骤3:若该轨迹点距离小于误差阈值距离D,则舍弃该点,以弦作为该轨迹的近似轨迹;若大于误差阈值距离,则以此关键点将曲线划分成两段,并对分割后的两段轨迹分别重复步骤1~3操作。
如此循环,直到所有距离均小于误差阈值距离,则保存这些关键点构成轨迹,即为压缩后的轨迹。轨迹压缩后的压缩率(compression ratio,RC)计算公式如式(1):
(1)
式中:M0和M1分别为原始轨迹压缩前后的轨迹点数目。同时,为了表征原始轨迹与压缩后轨迹之间的差距,引入平均距离误差S来衡量,计算公式如式(2):
(2)
式中:dist(pi)为原始轨迹中的第i个点距其压缩后对应的关键点的欧氏距离;n为原始轨迹的轨迹点数目。
2 航空器飞行轨迹聚类方法的改进
2.1 建立多维特征的轨迹相似性模型
设航空器飞行轨迹可表示为TR,则某条飞行轨迹i可表示TRi={TRi1,TRi2,…,TRij,…,TRin},其中n为该条轨迹的轨迹点数,且对于不同的飞行轨迹,压缩后每条轨迹的轨迹点数不一定相同。考虑到两轨迹点之间的位置、速度和航向属性,定义轨迹TRx内任一点TRxa到另一条轨迹TRy内任一点TRyb的多因素距离如式(3):
multidist(TRxa,TRyb)=wd·dist(TRxa,TRyb)+wv·dist(Vxa,Vyb)+wθ·dist(θxa,θyb)
(3)
式中:Vxa,Vyb,θxa和θyb分别为轨迹点TRxa和TRyb的速度和航向;dist(Vxa,Vyb)和dist(θxa,θyb)分别为两点之间速度属性和航向属性的欧式距离;wd,wv和wθ分别为位置、速度和航向属性的权重,权重因子的选择主要依赖于各机场的不同标准进离场程序,满足wd≥0,wv≥0,wθ≥0和wd+wv+wθ=1。为了消除各特征属性之间,不同量纲会对多因素距离结果产生影响,采用归一化处理各特征属性,再进行距离的度量。
同样,定义基于Hausdorff距离的轨迹相似性度量方法,计算两条轨迹之间的距离,计算公式如式(4):
(4)
同理,求出r(TRy,TRx),再利用公式R(TRx,TRy)=max{r(TRx,TRy),r(TRy,TRx)},得到两条轨迹间的相似性距离,最后求出所有轨迹间的相似性矩阵。
2.2 模糊C-均值聚类的实现
模糊C-均值聚类算法(FCM)[14]是用隶属度确定每个数据点属于某个聚类程度的一种聚类算法,其聚类准则是求U,V,使得J(U,V)取得最小值。应用FCM将给定的样本空间X={x1,x2,…,xn}划分为c类,分类结果用隶属度矩阵U=(μij)c×n表示;μij表示第i个样本属于第j类的隶属度,μij满足式(5):
(5)
定义目标函数:
(6)
式中:m为幂指数,且m>1;vj(j=1,2,…,c)是聚类中心。
2.3 改进的模糊C-均值聚类
由于FCM采用的梯度法搜索方向总是沿着能量减小的方向,使得算法本身对初始值敏感。针对FCM存在的问题,采用将粒子群(PSO)算法和禁忌搜索(TS)算法相结合的组合优化算法,通过PSO算法的全局寻优能力和TS算法跳出局部极值的能力得到最优初始聚类中心,从而更加快速、有效地收敛到全局最优解。具体步骤如下:
步骤1:输入待聚类数据,给定FCM算法和组合优化算法的初始参数,如幂指数m,最大迭代次数Tmax,学习因子c1、c2,速度上下界vmax、vmin,惯性权重w,邻域解、候选解个数及禁忌表长。
步骤2: 初始化粒子群规模n,随机选择s个聚类中心组成n×s个粒子。设初始位置为Xi,并随机产生此n个粒子的随机速度,t=0。
步骤3: 按照式(6)计算每个粒子个体的适应度值fit(i),并找出个体极值pbest(i)和全局极值gbest(i)。再比较当前粒子群的局部和全局最优位置和每个粒子的适应度值,最后决定是否替换。
步骤4:根据式(7)和式(8)更新每个粒子的速度和位置,如果满足误差阈值要求或算法的迭代次数则继续下一步,否则返回步骤3。
V′i=w·Vi+c1·r1·[pbest(i)-Xi]+c2·r2·(gbest-Xi)
(7)
X′i=Xi+Vi
(8)
步骤5:以PSO算法的输出解作为TS算法的初始解,置空禁忌表。
步骤6:如果满足收敛准则直接输出最优初始中心;如果不满足,根据领域函数的定义得到当前解的所有(或若干)邻域解,并从中确定若干候选解。
步骤7:根据藐视规则来判断每个候选解是否均满足,若满足,则将此候选解认定为当前解,同时将最早放入禁忌表的对象用当前解的对象替换;若不满足,则判断候选解的禁忌属性,此时当前解为非禁忌对象对应的最佳解,同时将最早放入禁忌表的对象用与之对应的禁忌对象替换。
步骤8:判断是否满足收敛准则,如果满足则直接输出FCM的最优初始中心;如果不满足,返回步骤6。
3 算例仿真
3.1 飞行轨迹的压缩处理
以华北地区某机场终端区第16R号跑道的679条进场历史轨迹为研究对象,共有694 239个原始轨迹点。应用Top-Down Time Ratio算法压缩飞行轨迹,误差阈值距离D是一个很关键的参数指标,直接决定了是否保留某些关键特征点。试验取一条轨迹点数目为941个的飞行轨迹为研究对象,选择5个不同的误差阈值距离来衡量其对轨迹特征点提取的影响,从而确定可以更好反映轨迹分布的轨迹特征点数目,结果如表1和图2。
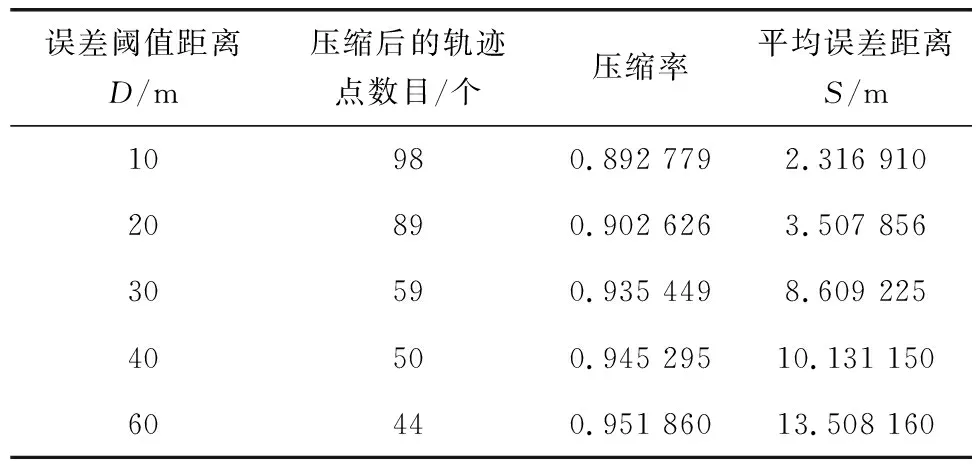
表1 轨迹压缩算法的误差阈值对比Table 1 Error threshold comparison of trajectory compression algorithm
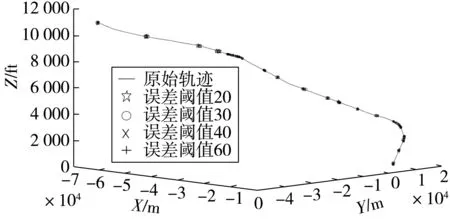
图2 不同误差阈值距离对应的轨迹压缩Fig. 2 Trajectory compression corresponding to different error threshold distances
由表1可以看出,随着误差阈值距离D的不断增加,轨迹压缩效果越来越好,但平均误差距离也进一步增大。同时由图2明显地看到,轨迹的关键点多集中在曲线转弯处,近似直线段用较少的点来表征,且随着误差阈值距离的减小,更多的特征点被提取出来用来描述近似直线段特征。同时为了检验笔者算法在轨迹压缩时的精确性和稳定性,同现有的DP算法进行对比,以平均距离误差S作为误差指标,结果如图3。
由图3可知,在相同的压缩率下,Top-Down Time Ratio算法的平均距离误差更小些,能较好地还原原始轨迹。此外,随着压缩率的不断增加,两者的误差均呈上升趋势。因此,在保证飞行特征和有效降低数据规模的前提下,此处暂取误差阈值距离为30 m来压缩轨迹。
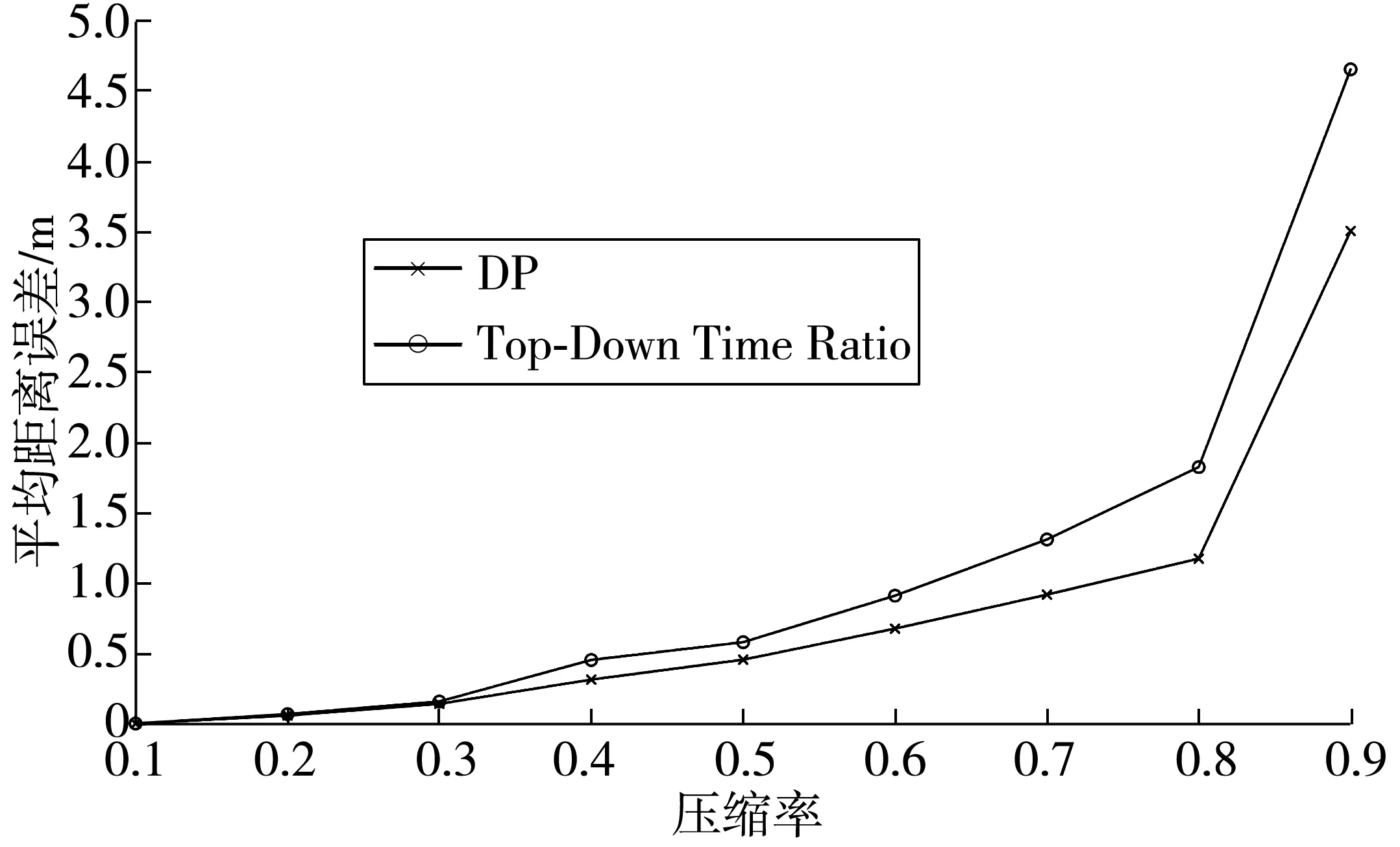
图3 不同压缩率下的平均距离误差Fig. 3 Average distance error under different compression ratios
3.2 飞行轨迹聚类分析
在不同的飞行阶段,要均衡体现出位置、速度和航向对轨迹的影响,需要选取不同的权重值。经试验,取w1=0.7,w2=0.2,w3=0.1。利用式(3)计算出所有轨迹间的相似性距离,得到轨迹间的相似性矩阵。
设置FCM算法参数。取聚类数c=60,即飞行轨迹的聚类中心数;幂指数m=2;目标函数的终止容限为1×10-6;最大迭代次数Tmax=100。
设置PSO算法参数。取粒子群规模N=50;学习因子c1=2,c2=2;最大速度Vmax=2,最小速度Vmin=-2;惯性权重w=0.6;最大迭代次数Tmax=100。
设置TS算法参数。取禁忌表长为25;邻域解和候选解均取20个;终止判据是最大迭代次数为100。
应用FCM和TSPSO_FCM算法对轨迹间的相似性距离进行聚类,已知该机场至少有3条传统的标准进场程序,此处暂取聚类数为3类,聚类结果如图4。
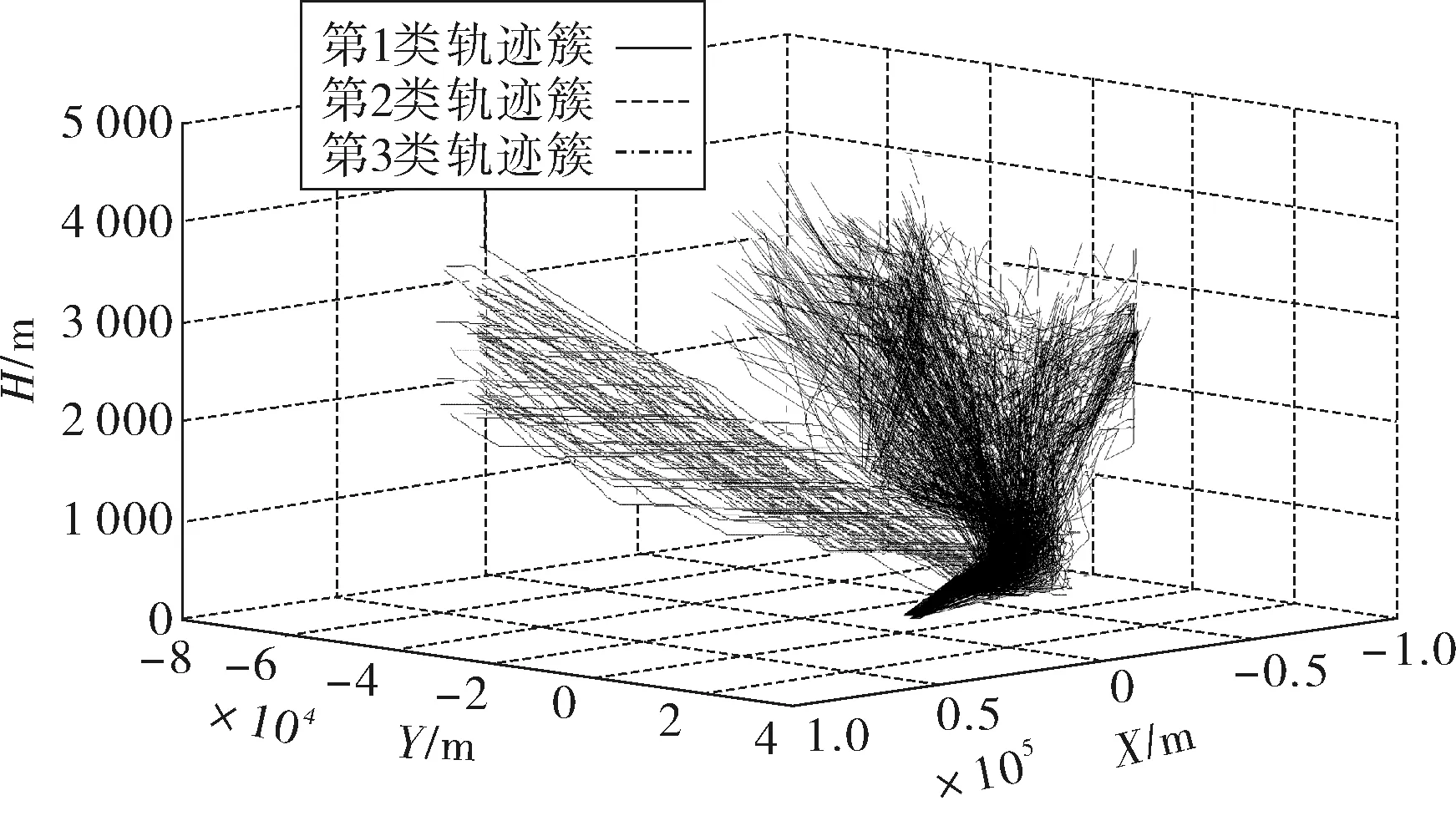
图4 TSPSO_FCM算法的飞行轨迹聚类Fig. 4 Flight trajectory clustering of TSPSO_FCM
由于聚类算法是以最终保证组内相似度最高,组间相似度最低为聚类原则,结合FCM聚类原理及式(7)知可用目标函数值来衡量聚类效果,FCM与TSPSO_FCM算法各自的聚类性能结果如图5。
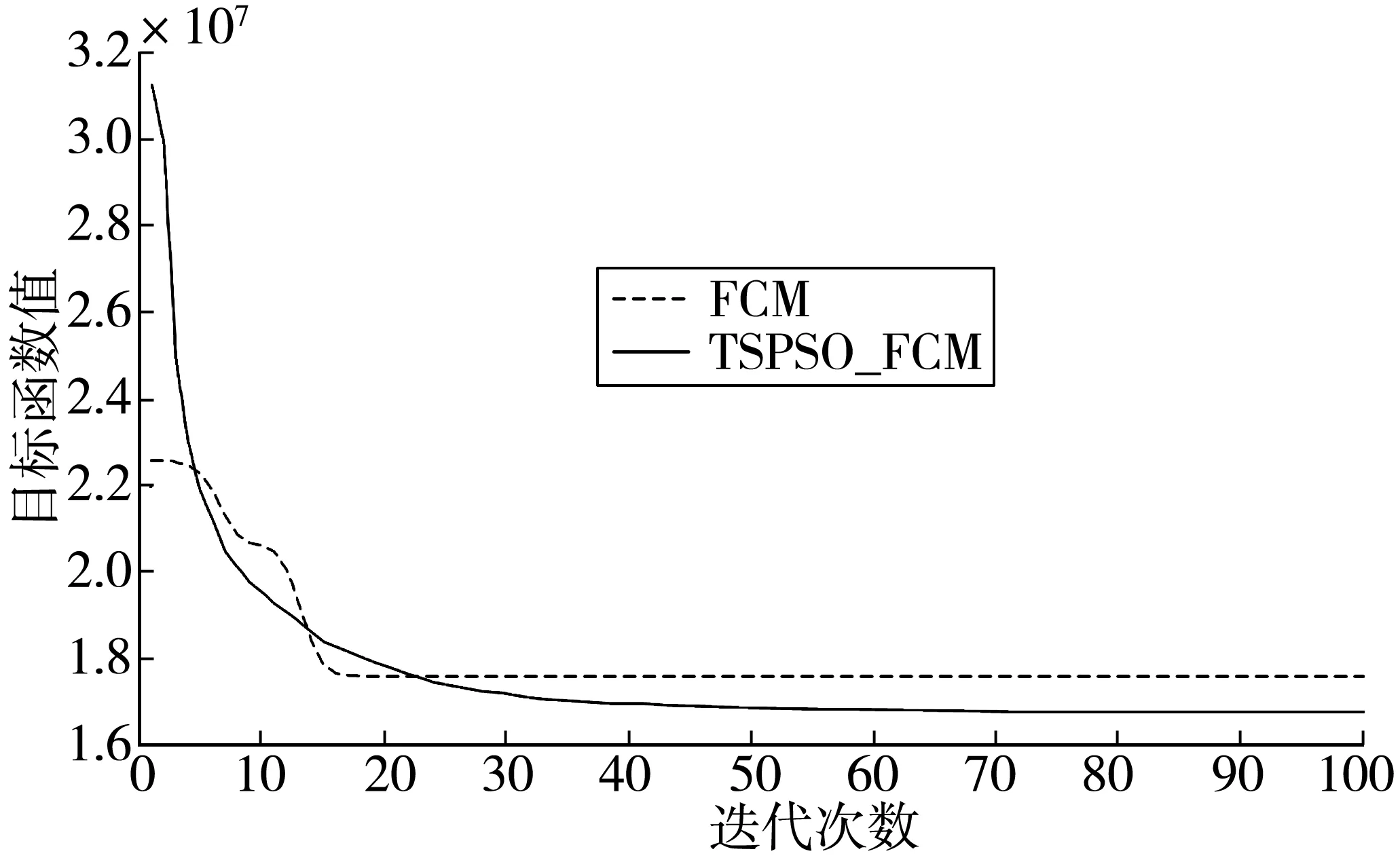
图5 基于目标函数值的聚类性能比较Fig. 5 Comparison of clustering performance based on objective function values
由图4可以看出,TSPSO_FCM 算法逐渐减小并且趋于稳定。单独 FCM 算法的目标函数值在逐步减小的过程中没有出现反复情形,这也说明基于梯度下降的 FCM 算法在样本空间进行聚类时就有可能陷入局部极小且目标函数值较大。
3.3 参数变化对聚类效果的影响
针对在飞行轨迹压缩过程中不同的误差阈值、聚类数会直接影响最终的聚类结果。因此,在其他各类参数不变的情况下,取不同的误差阈值距离和聚类数进行试验,结果如表2。
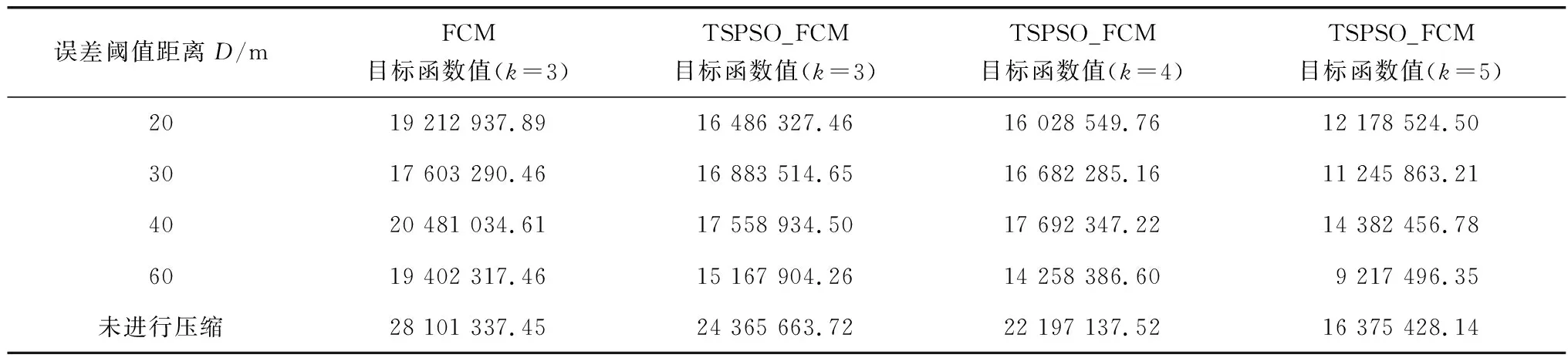
表2 误差阈值距离和聚类数的影响Table 2 Influence of error threshold distance and number of clusters
由表2可以看出,当误差阈值距离逐步增大时且对比未进行轨迹压缩时,使用 TSPSO_FCM算法得到的目标函数值相比FCM算法更优,聚类效果更好。将飞行轨迹簇k取4类和5类进行聚类时,TSPSO_FCM算法得到的的目标函数值均小于k取3类时,这是因为随着聚类个数的增多,各类间的紧凑性变大,导致目标函数值变小。由图6可知,当轨迹簇分为4类时,从东南方向进场的航空器飞行轨迹分为两簇,符合该终端区的标准进场程序;当轨迹簇分为5类时,很明显地看到识别出了一种不同于机场传统进场程序的新的飞行模式。经验证可知,该飞行模式下的航空器飞行为繁忙时段需调配航空器安全间隔,由管制员直接引导航空器进场所形成。
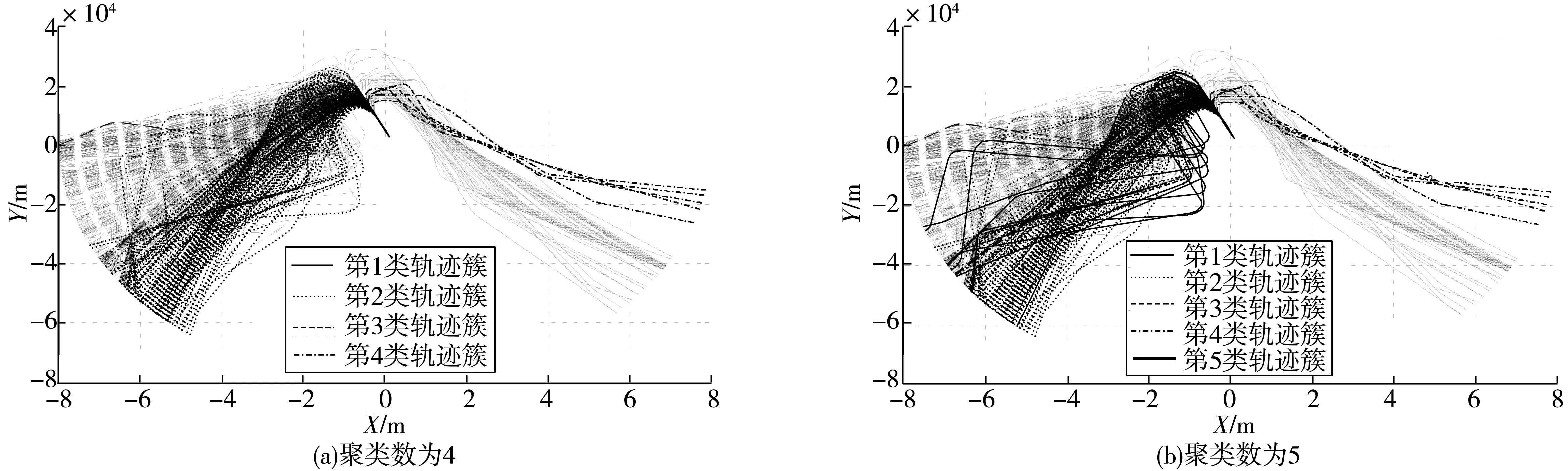
图6 不同聚类数对应的飞行轨迹簇Fig. 6 Flight trajectory cluster corresponding to different cluster numbers
因此,该方法通过分析参数的变化对聚类结果的影响,有效地挖掘出了该机场终端区的航空器进场飞行模式,为该机场由传统程序向基于性能导航(PBN)程序转变提供重要参考。
4 结 论
1)在保持较低失真率的情况下,采用基于时间比的自顶向下算法压缩飞行轨迹降低了计算开销,提高了轨迹数据分析能力。
2)建立基于多维特征属性的相似性模型,并结合组合优化算法改进FCM算法,避免了单独使用FCM聚类易于陷入局部最优的缺陷。试验结果表明,改进的FCM算法具有很强的全局搜索能力,降低了FCM算法对初始值的敏感度,可以得到较优的满意解。
3)飞行轨迹聚类时参数的变化会直接影响聚类算法对航空器飞行模式的挖掘能力,对于重新设计和优化传统飞行程序具有重要参考价值。
