冰棱对三维覆冰导线气动力特性影响研究

祝 贺， 王 刚， 郭 鑫

(东北电力大学 研究生院，吉林 吉林 132000)

高压输电导线覆冰通常是由于空气中的过冷却水滴撞击在导线上冻结，过冷水撞击导线瞬间没有将水滴完全冻结，部分水滴在重力和风速作用下流向导线下部并出现二次冻结，形成了独特覆冰形态——冰棱。冰棱的产生改变了覆冰导线横截面形状，由稳定截面变成非稳定截面。这种横变截面冰棱覆冰导线在风荷载作用下产生的升力和阻力可能引起导线出现低频、大幅度舞动。输电导线舞动会引起线路倒塔、断线、掉串以及短路、跳闸和大面积停电等事故，给电力系统带来重大损失，威胁电网的安全稳定运行和供电系统运行的可靠性[1-2]。

目前很多国内外学者对覆冰导线气动失稳引起导线舞动的基本特性进行了研究，王琼等对D形覆冰四分裂导线气动力进行了风洞试验研究，分析了不同导线型号、分裂间距下分裂导线的气动力特性[3]；楼文娟等[4-5]利用风洞试验分析了不同厚度和不同初凝角下D形覆冰分裂导线的气动力特性；文献[3-5]都是从导线D形覆冰角度进行研究，分析了覆冰厚度、风攻角、分裂间距等因素下覆冰导线气动力。马文勇等[6-7]对新月形覆冰导线进行气动力研究，分析了覆冰导线驰振稳定性；王琼等[8-10]通过数值模拟对新月形四分裂覆冰导线舞动特性进行研究；严波等[11]对新月形偏心覆冰导线进行了升力和阻力系数进行了试验；文献[6-11]选择了新月形覆冰类型进行研究，通过分析分裂导线气动力特性研究覆冰导线驰振稳定性。陈友慧等[12]对扇形覆冰导线气动力特性进行研究，分析了扇形覆冰导线舞动特性；李新民等[13]对扇形覆冰导线进行了空气动力学试验研究，分析了影响覆冰导线舞动因素；文献[12-13]考虑了扇形覆冰导线气动力特性，分析了扇形覆冰导线发生舞动概率。以上研究都关注稳定截面覆冰导线气动力及舞动特性，并分析了覆冰厚度、风攻角、分裂数等对其产生的影响，而忽略了非均匀横截面覆冰导线气动力及其相互影响对导线舞动影响。为此利用ANSYS软件，建立三维五冰棱覆冰导线绕流场模型并进行数值模拟分析，监控冰棱覆冰导线的阻力系数、升力系数，根据Den Hartog理论计算驰振力系数，研究覆冰导线驰振稳定性。

1 流场数学模型

1.1 流体运动方程

任何流体流动都要受到物理定律的约束，连续介质模型条件下，质量守恒定律在流体流动力学中的表现形式为连续性方程，同时在模型中物质的速度和密度都可用三维坐标函数表示。其控制方程为连续性方程[14]

(1)

式中:u，v，w为速度矢量;对于不可压缩流体，ρ为常数。

湍流现象是高度复杂，目前没有一种模型能对所有湍流现象进行模拟，本文拟选用Fluent提供的湍流黏度考虑了湍流剪应力的SSTk-w湍流模型，其流动方程[15]

Gk-Yk+Sk

Gw-Yw+Dw+Sw

(2)

式中:Gk为湍流动能;Gw为w方程;Γk,Γw分别为k与w的有效扩散项;Yk,Yw分别为k与w的发散项。

1.2 气动力参数计算

覆冰导线气动力参数主要由两方面表示，其一，覆冰导线阻力和升力；其二，无量纲参数阻力系数和升力系数。阻力系数和升力系数分别可由下式表示为[16]

CD=2FD/(ρU2LB)

(3)

CL=2FL/(ρU2LB)

(4)

式中:CD、CL分别为阻力系数和升力系数；FD为覆冰导线阻力，阻力方向以来流方向为正；FL为覆冰导线升力，升力方向以来流方向顺势针旋转90°为正；ρ为环境空气密度，其取值为1.225 kg/m3；U为来流风速均值，m/s；B为横截面覆冰导线模型特征长度；L为横截面覆冰导线模型长度。

1.3 覆冰导线横向驰振分析

非均匀横截面覆冰导线在风荷载作用下，产生升力和阻力导致横截面覆冰导线出现驰振现象。由Den Hartog驰振机理，在相同风攻角下，升力系数对风攻角倒数与阻力系数的和值大于零时，振动系统不发生驰振；升力系数对风攻角倒数与阻力系数的和值小于零时，振动系统出现失稳驰振，该驰振机理可表达为[17]

(5)

式中，α为非均匀横截面覆冰导线风攻角。

2 三维冰棱覆冰导线数值模拟分析

2.1 建立冰棱覆冰导线模型

传统二维流场对沿导线方向均匀覆冰导线是适用的，但对于非均匀横截面冰棱覆冰导线具有局限性，不能充分表达非均匀横截面覆冰导线流场特性。构建三维五冰棱覆冰导线计算流场，流场长为4 m、高为4 m、宽为0.125 m，冰棱覆冰导线中心点位于三维流场中心，其xy坐标为(2,2)，距离左侧边界2 m，距离右侧边界2 m，距离上下流场壁面均为2 m，将x轴正方向设置为水平风速来流方向，将x轴正方向逆时针旋转90°即为y轴正方向，z轴为导线长度方向即导线展向方向，三维五冰棱计算流域尺寸和坐标图见图1。三维五冰棱覆冰导线模型覆冰后直径为50 mm，导线长125 mm[18]，将覆冰导线模型等长度划分为5部分，每部分有且只有一个冰棱存在，冰凌三维形状为圆锥形(水平切掉尖端一小部分)，相邻冰棱间距为25 mm，冰棱长度为60 mm，冰棱覆冰导线模型尺寸图见图2。

2.2 数值模拟计算

利用ANSYS ICEM CFD软件对三维五冰棱覆冰导线流场进行结构化网格划分，流场网格总数量为1 526 846，覆冰导线周围边界层采用外O形网格划分[19]；同时为保证模拟精确度，对边界层网格进行局部加密，边界层相邻网格距离不大于1 mm，网格划分见图3。

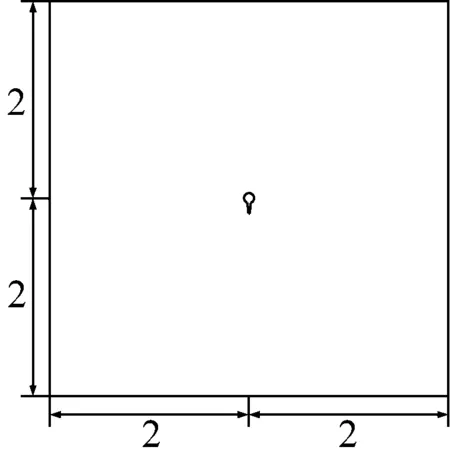
(a) 三维流域正视尺寸(m)

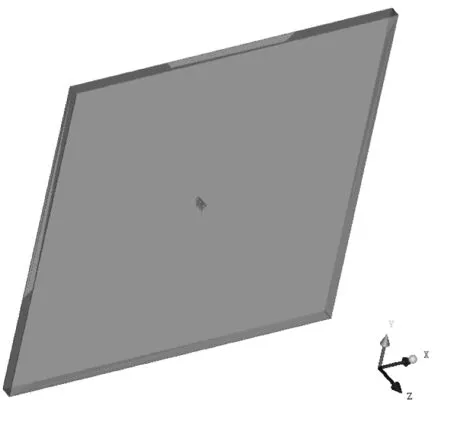
(b) 三维流域坐标

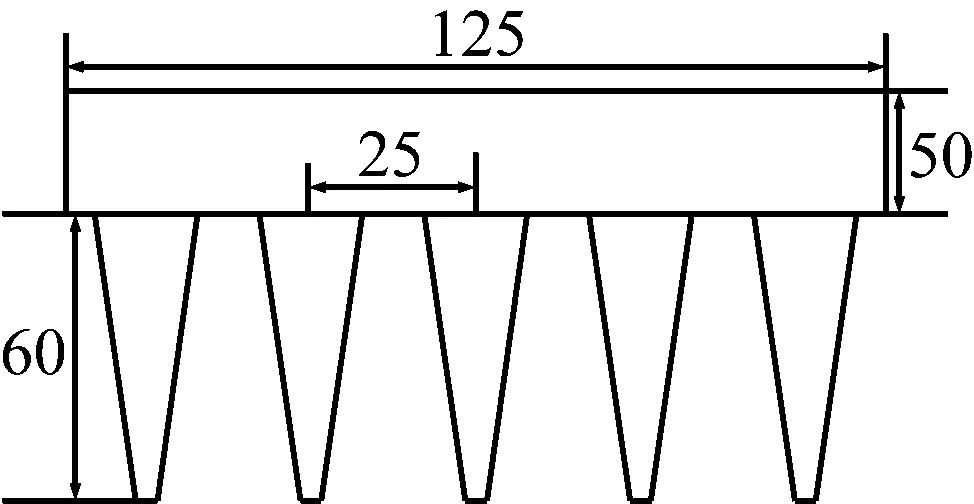
图2 三维五冰棱覆冰导线尺寸(mm)

(a) 整体网格

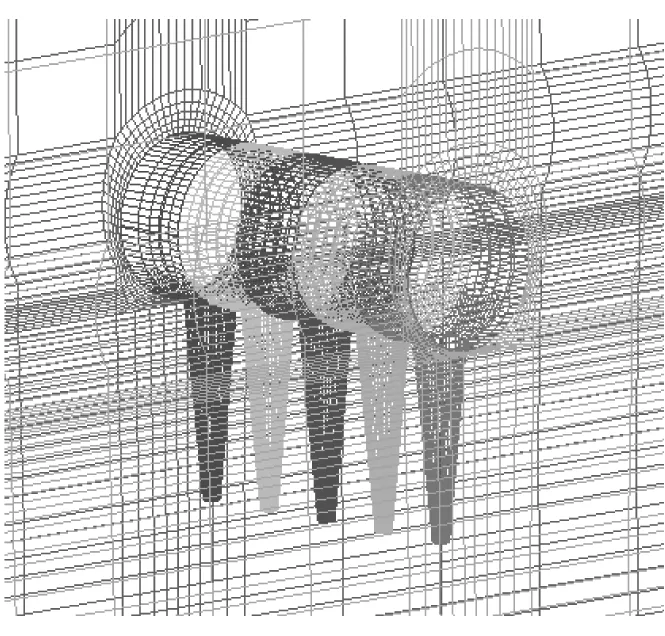
(b) 局部加密网格

为分析研究三维五冰棱覆冰导线在风场作用下气动力及舞动特性，将冰棱覆冰导线沿z轴正方向等长度进行划分，长为125 mm冰棱覆冰导线模型被分为5部分；每部分长为25 mm，沿z轴正方向分别编号定义为1～5[20]。为研究相邻冰棱之间相互影响关系，在ANSYS FLUENT中选取编号为3冰棱覆冰导线节段进行气动力参数监视，其节段划分见图4。

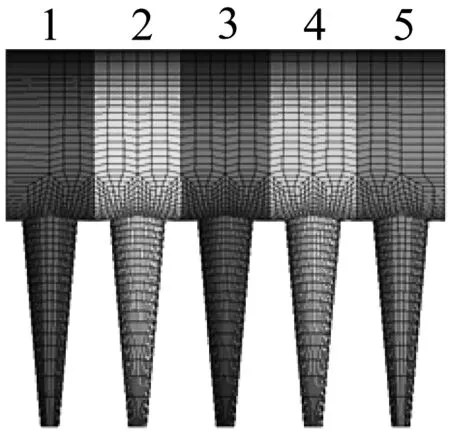
图4 三维五冰棱覆冰导线节段

计算流域边界条件设置：当0<α<45°时，左边界和上边界为风速入口，右边界和下边界为压力出口；当α=45°时，左边界为风速入口，右边界为压力出口；当45°<α<135°时，左边界和下边界为风速入口，右边界和上边界为压力出口；当α=135°时，下边界为风速入口，上边界为压力出口；当135°<α<180°时，右边界和下边界为风速入口，左边界和上边界为压力出口。左右壁面均设定为对称面(symmetry)，其余未定义壁面均默认为无滑移固面(no slip wall)，流域边界条件设置见图5。

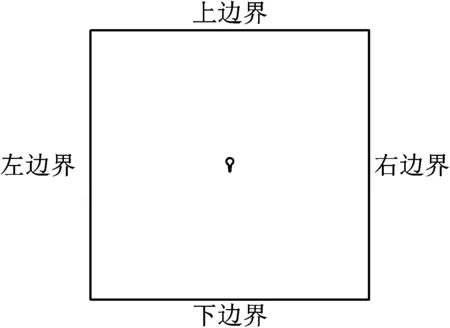
图5 计算流域边界条件

计算流域风攻角范围为0°～180°，设定x轴正方向顺时针旋转45°为0°风攻角，风攻角以逆时针方向每隔10°进行一次调整。相同风攻角下分别取10 m/s、15 m/s、20 m/s、25 m/s风速进行模拟计算，时间步长为0.05，计算100步，计算流场风攻角见图6。

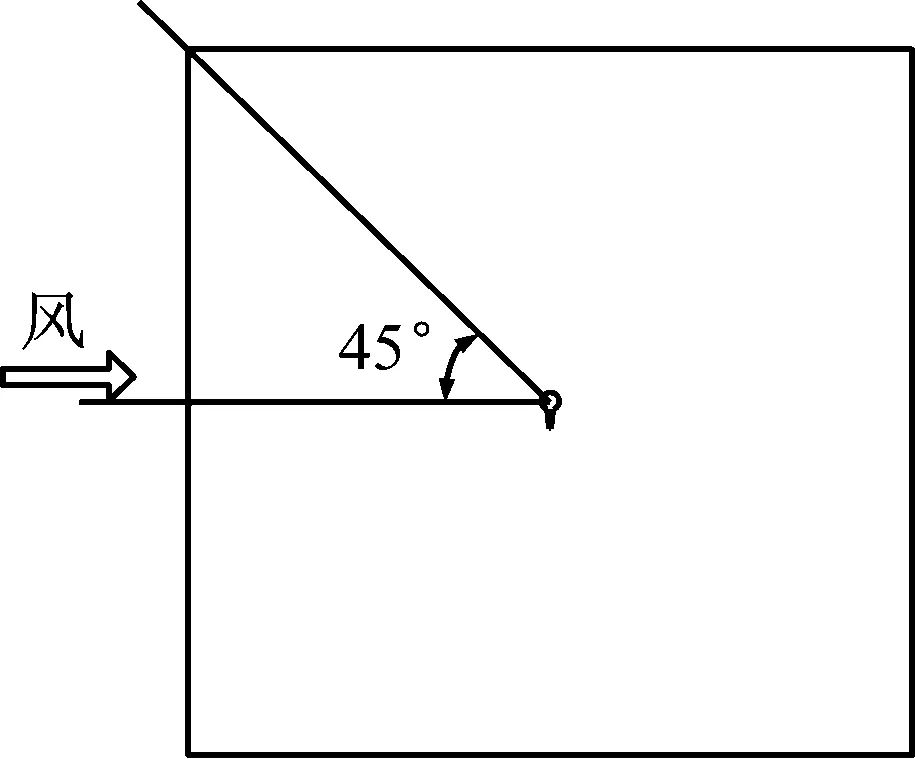
图6 流场风攻角

3 冰棱覆冰导线气动力数值模拟结果

3.1 冰棱覆冰导线流场特性

为研究冰棱覆冰导线表面不同位置处压力及周围速度特性。选取45°风攻角，来流风速为15 m/s时，不同时刻冰棱覆冰导线迎风侧压力和覆冰导线周围速度进行分析。图7为三维流场在45°风攻角，来流风速为15 m/s时，不同时刻覆冰导线压力分布云图。

由图7可知，不同时刻迎风侧压力分布存在差异，最大压力主要分布在圆柱迎风面下半部分和覆冰导线冰棱上半部分，最小压力分布于覆冰导线圆柱顶部。同时可知，不同时刻圆柱与冰棱连接处压力大小有明显变化，在2.25 s、2.5 s时刻圆柱与冰棱连接处压力处于最大值，其值为，在2.75～3.5 s期间连接处压力由变为。

2.25

2.5

2.75

3.0

3.25

3.5

冰棱迎风侧压力分布呈周期性变化，在2.25～3.0 s期间，最大压力覆盖面积逐渐减小，在3.0～3.5 s期间，最大压力覆盖面积逐渐增大，在3.5 s后覆盖面积又逐渐减小。同时最大压力变化时冰棱迎风侧压力分布始终呈现为“圆锥面”分层分布。

图8为三维流场在45°风攻角，来流风速为15 m/s时，节段3中心点截面不同时刻速度云图。

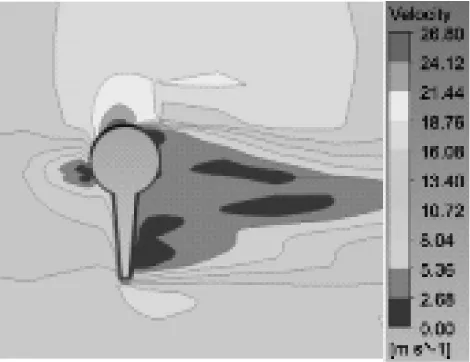
2.75

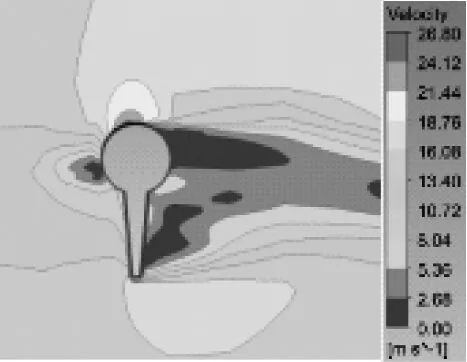
3.25

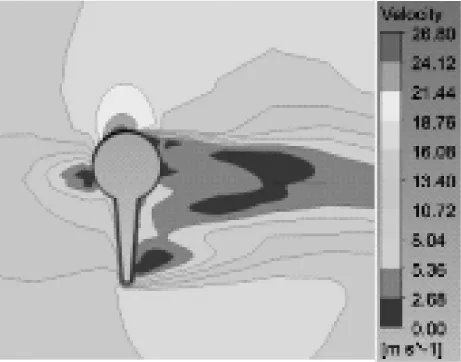
3.5

由图8可知，不同时刻节段3截面速度分布有明显差异，随着时间推移冰棱底端对速度加速影响范围逐渐增大，对背风侧低速区域有明显挤压效应。

3.2 全攻角下冰棱覆冰导线气动力特性分析

选取位于三维五冰棱覆冰导线模型中间节段3作为对象分析研究，图9为节段3在不同风速和攻角下的升力和阻力系数。

由图9可知，阻力系数随着攻角增大，趋势表现为先增大、后减小、再增大。在风攻角50°～60°区间取得阻力系数最大值，在风攻角130°～140°区间取得阻力系数最小值。随着风速增加，阻力系数最大和最小值均减小，但变化幅度小。升力系数总体呈现为先减后增。在风攻角为20°时，升力系数取得最大值，且随着风速增加，升力系数最大值增加；在风攻角为100°和170°时，升力系数取得最小值，并随着风速增加，升力系数最小值增加。

3.3 不同因素影响冰棱覆冰导线气动力特性

三维冰棱覆冰导线在风荷载作用下表现出来的气动力参数特性与多种影响因素有关，考虑三维冰棱覆冰导线自身结构，分析其对覆冰导线气动力的影响有助于分析研究冰棱覆冰导线气动力特性。

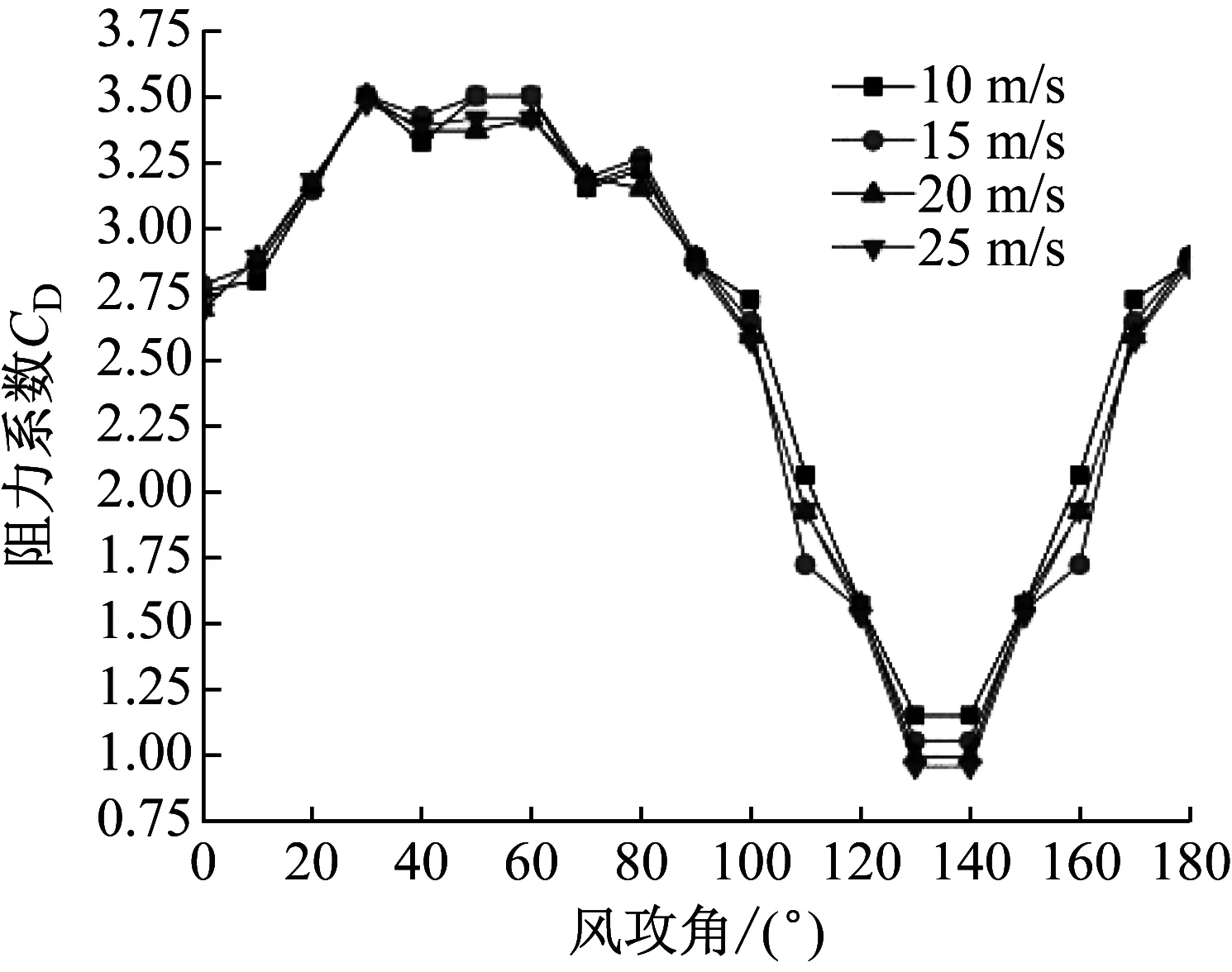
(a) 阻力系数

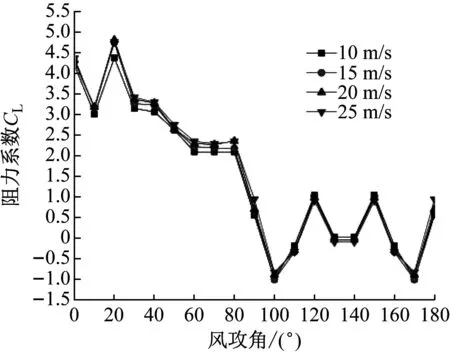
(b) 升力系数

3.3.1 冰棱长度对气动力的影响

选取冰棱长度分别为60 mm、80 mm、100 mm，风速为15 m/s时进行分析，图10为不同冰棱长度下覆冰导线气动力参数。

由图10可知，随着冰棱长度增加，在任意风攻角下覆冰导线阻力系数均增大。冰棱长度增加没有改变阻力系数最大值和最小值出现风攻角，在风攻角为40°时取最大值，在风攻角为130°～140°区间取最小值。升力系数受冰棱长度影响并不像阻力系数那样明显，整体趋势表现为先减小再增加。由于不同冰棱长度风场相互影响存在差异，导致升力系数变化复杂。在风攻角为10°时，取得最大值且冰棱长度100 mm值最大；在风攻角为100°和170°时，取得最小值且冰棱长度60 mm值最小。

3.3.2 冰棱间距对气动力的影响

考虑冰棱间距对覆冰导线气动力的影响，选取冰棱间距分别为25 mm、30 mm、35 mm，风速为15 m/s时进行分析，图11为不同冰棱间距下覆冰导线气动力参数。

由图11可知，阻力系数在风攻角40°时，取得最大值且冰棱间距25 mm值最大；在风攻角130°～140°区间时，取得最小值且冰棱间距30 mm值最小。升力系数受相邻冰棱间距影响较大，随着攻角增加，升力系数先减小再增加。相邻冰棱间距为25 mm时，随着攻角增加，升力系数变化幅度最大。

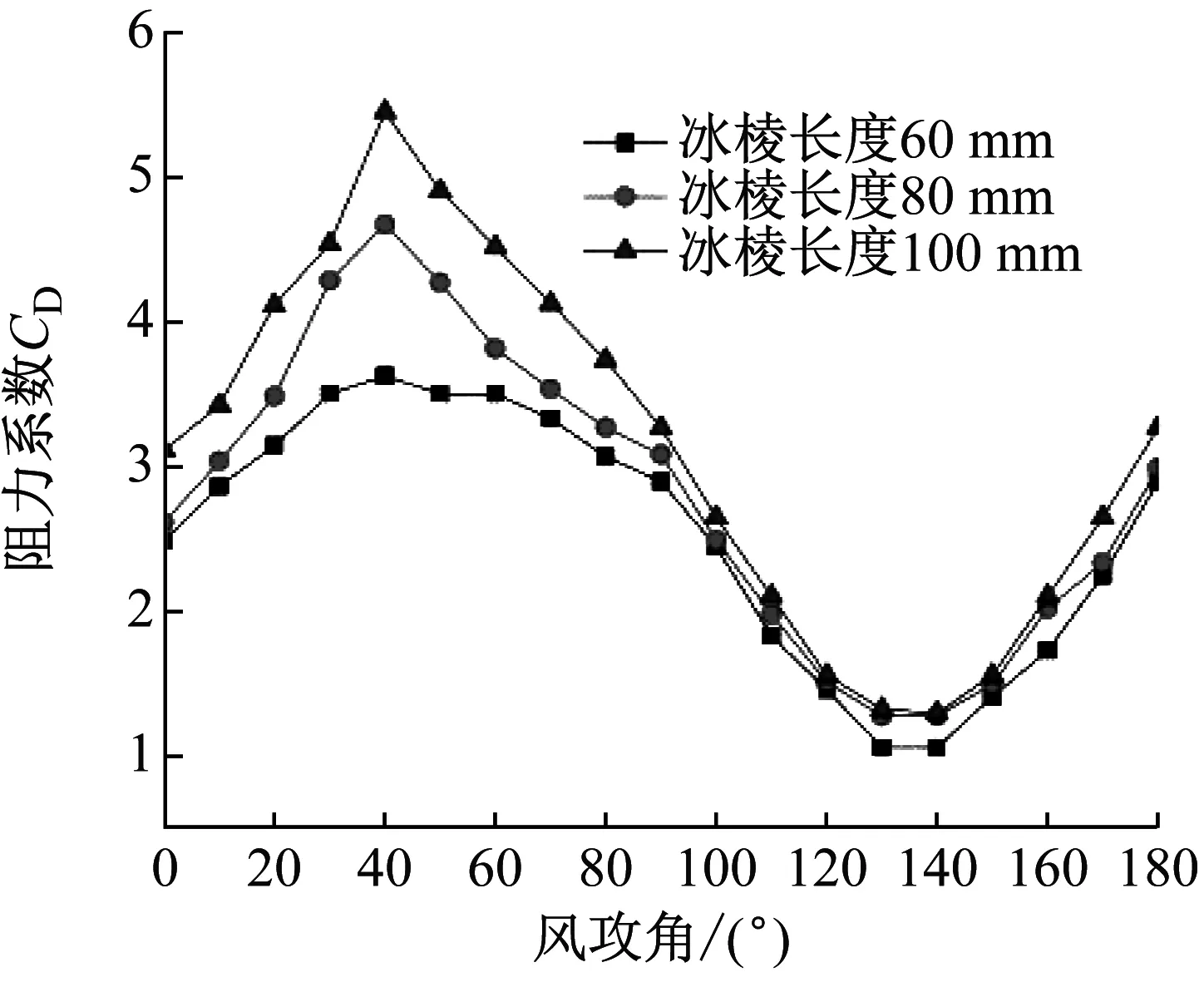
(a) 阻力系数

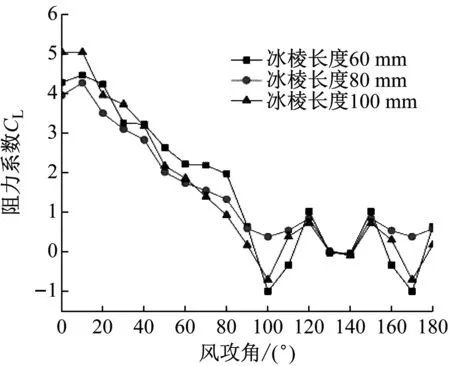
(b) 升力系数

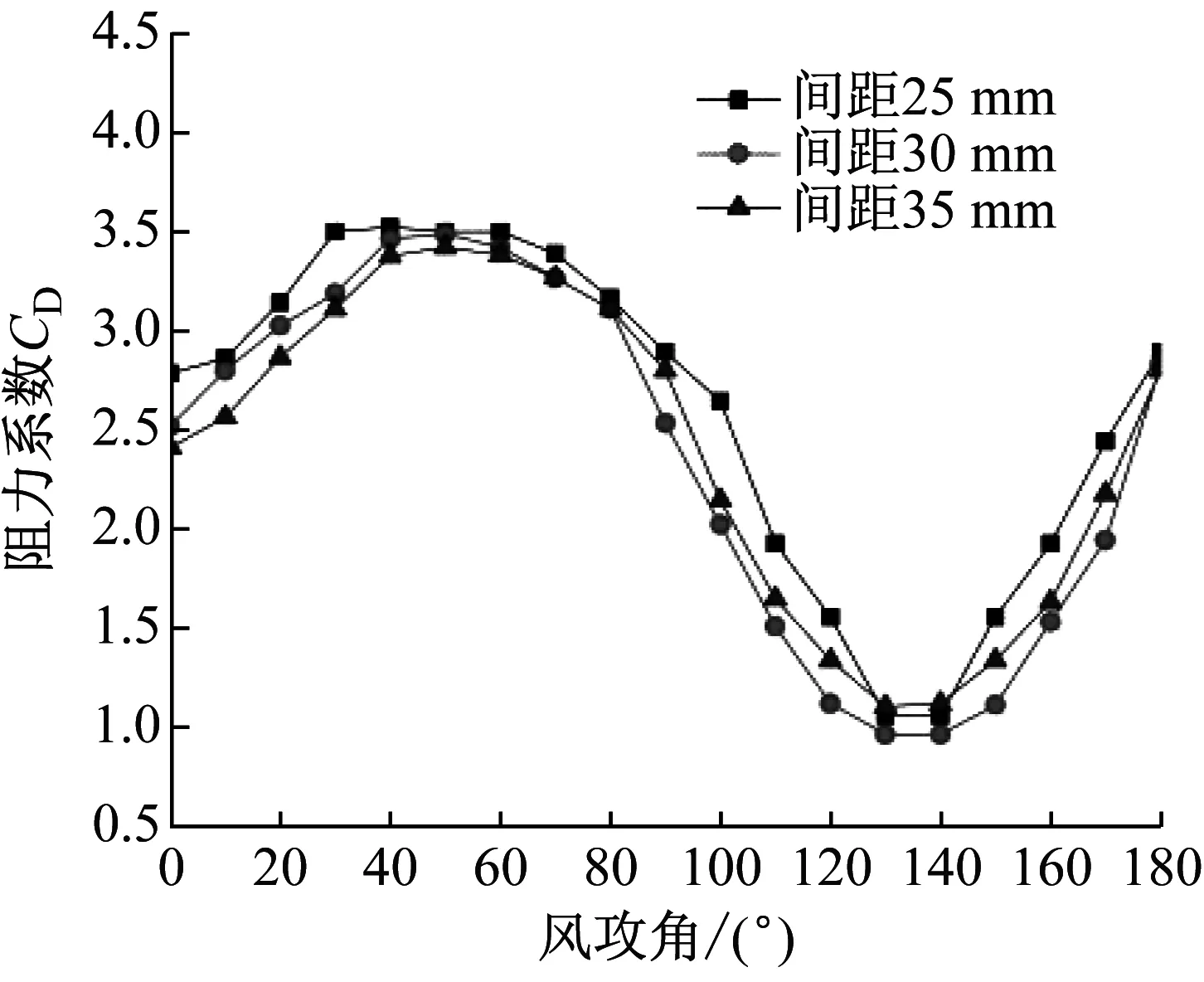
(a) 阻力系数

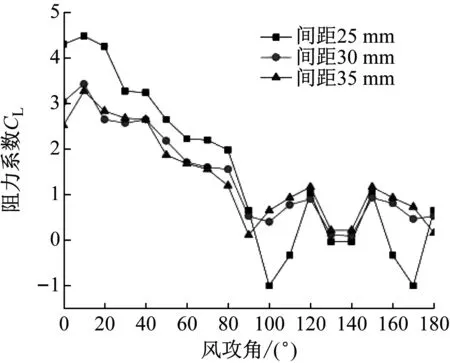
(b) 升力系数

3.4 全攻角下三维冰棱覆冰导线驰振力系数

通过式(5)计算可得到平均升力系数随风攻角变化曲线的斜率值与平均阻力系数的和值，即驰振力系数。对于一个特定风攻角而言，∂CL/∂α可能取CL-α曲线的左侧曲线斜率或者右侧曲线斜率。两种情况下计算驰振力系数随风攻角变化的数值见图12，当任意风攻角处左侧驰振力系数和右侧驰振力系数均小于零(<0)时，认为冰棱覆冰导线出现驰振舞动。

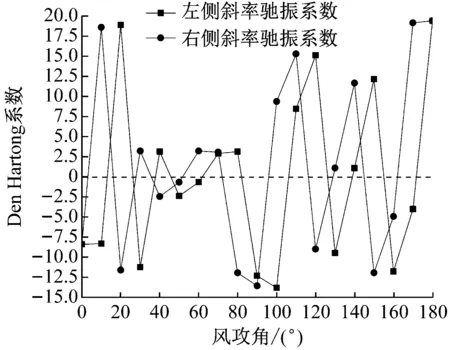
图12 三维冰棱覆冰导线驰振力系数(风速：15 m/s，间距：25 mm，棱长：60 mm)

由图12可知，当风攻角为50°、90°、160°时，通过式(5)计算得到的驰振力系数均为负值，表明在这些风攻角下冰棱覆冰导线处于非稳定状态，极易发生覆冰驰振舞动。

4 结 论

(1) 三维五冰棱覆冰导线迎风侧最大压力分布呈现周期性变化，主要分布在覆冰圆柱下半部分和冰棱上半部分；分布面积由大及小再由小及大，周期时间为1.25 s。说明覆冰导线上冰棱存在对覆冰导线流体绕流特性有极大的影响。

(2) 冰棱覆冰导线在风攻角50°～60°区间取得阻力系数最大值，在风攻角130°～140°区间取得阻力系数最小值；升力系数出现最大值和最小值风攻角分别为20°和100°、170°，且随着风速增加，升力系数最大值和最小值均有所增加。

(3) 随着冰棱长度增加，覆冰导线阻力系数最大值由3.42增长到5.47，升力系数在风攻角10°时，取得最大值且冰棱长度100 mm最大；在风攻角100°和170°时，取得最小值且冰棱长度60 mm最小。

(4) 根据Den Hartong覆冰舞动理论计算，三维五冰棱覆冰导线在50°、90°、160°风攻角时对应风攻角计算得左侧驰振力系数和右侧驰振力系数均小于零(<0)，表明冰棱覆冰导线处于非稳定状态，冰棱覆冰导线出现驰振舞动概率极大。