π型开口截面斜拉桥弯扭耦合涡激共振及气动减振措施研究

汪志雄， 张志田,2， 郄 凯， 吴长青

(1.湖南大学 土木工程学院风工程试验研究中心，长沙 410082； 2.海南大学 土木建筑工程学院，海口 570228)

随着经济和社会的发展，我国高速公路网的建设快速完善，斜拉桥成为跨越山谷、河流、湖泊等的主要桥型，随着其跨径的增大，主梁的自重对桥梁的影响就越大。π型组合梁具有自重轻、施工方便、造价低等特点，成为了众多大跨径斜拉桥的首选断面。但由于其扭转刚度低及气动稳定性差的特点，工程实践中这类桥更容易出现风致振动[1]。在桥梁可能发生的各类气弹现象中，涡激共振是低风速下很容易出现的一种，其原理是由钝体尾流中旋涡的交替脱落所致。这类风振具有自激限幅性质且对结构阻尼以及桥梁断面外形的微小变化较为敏感[2]。通常情况下，钝体断面漩涡脱落的特性可以用一个无量纲参数斯托罗哈数表示[3]。对于给定的钝体断面，其斯托罗哈数通常是一定的，意味着涡脱频率随风速线性增加。当涡脱频率接近结构某一阶固有频率时，会引起结构发生大幅振动，并形成风速锁定区间。涡激共振不会对结构造成毁灭性的损害，但能引起结构的疲劳损伤、降低结构使用的舒适度，从而受到了众多学者的关注[4-6]。

常用的结构风振抑制措施可分为空气动力学措施和机械阻尼措施[7]。空气动力学措施是通过改变结构的气动外形来达到减小风致振动的目的。Koga[8]针对π形断面端部的气动措施进行了系统的试验研究；钱国伟等[9]通过改变检修道截面形式及风嘴角度来控制π型叠合梁的涡振；杨光辉等[10]通过改变π型截面梁底部中央稳定板长度及栏杆的透风率来研究对涡振性能的影响；李欢等[11]分析了下稳定板及隔流板等气动措施对施工阶段π性主梁涡激振动性能的影响；Irwin[12]则针对π形断面底部稳定板的气动控制效果进行了介绍。机械阻尼措施主要通过外加阻尼器来提高结构阻尼，从而达到抑制风致振动的目的，实际工程应用中由于其造价昂贵、且维护困难而很少采用。

旋涡脱落即可引起桥梁弯曲振动，也可引起扭转振动。通常情况下，大跨桥梁的弯曲与扭转频率存在明显的差异，扭弯频率比一般达到1.4以上，因此一般不存在弯曲与扭转同时发生的涡激共振。已有涡激共振相关文献均针对单自由度的振动进行研究，即竖弯和扭转涡振之间是相互独立的。

本文针对一拟建开口截面钢-混π型叠合梁斜拉桥主梁断面，通过节段模型风洞试验，揭示了该桥的耦合涡激共振特性，探讨耦合涡激共振的成因与有效的涡激振动气动抑制措施。

1 研究背景

设计中的某大桥位于山区峡谷地带，大桥主桥结构为(60+130+420+130+60)m五跨π型开口断面钢混叠合梁斜拉桥，主梁采用“工”字型钢纵梁、横梁、小纵梁通过节点板及高强螺栓连接形成钢构架，构架上架设预制桥面板，梁宽29 m，梁高3 m，两“工”字钢纵梁梁肋间距26.5 m，跨中点到正常水位的距离达205 m，桥塔最大高度达250 m，在相同类型的桥梁中，比同跨径的东海大桥桥塔高出100余米，即使跟主跨926 m的鄂东长江大桥的塔高相比仍高出12 m。开口断面具有扭转刚度小、气动外形复杂、易出现涡旋脱离等特点，为了保证大桥在施工和运营阶段的安全性及舒适性，必须对其开展风洞试验研究。整个桥的布置及主梁断面分别如图1和图2所示。

图1 立面图和平面图(m)

图2 主梁标准断面图(m)

2 节段模型风洞试验

2.1 模型设计参数

根据实桥主梁截面尺寸和风洞试验段尺寸及试验要求，选取节段模型的缩尺比λL为1∶50。刚性模型桥面板由6061T硬铝板和ABS板贴合而成，以保证外形的几何相似性，边主梁采用不锈钢薄板焊接而成，确保模型的整体刚度，成桥状态防撞栏杆及检修道栏杆用ABS板由电脑雕刻制成。试验时所采用的参数如表1所示，图3为悬挂于风洞中的刚性节段模型。

表1 节段模型试验参数

图3 节段模型风洞试验悬挂

2.2 涡振性能分析

针对图2所示的标准断面，首先进行风攻角为+3°与0°时测试，对应的竖弯阻尼比为0.52%、扭转阻尼比为0.53%。模型试验结果计算实桥涡振幅值，除了考虑断面几何缩尺比的变换，还需要引入幅值修正系数，来考虑全桥参振的影响，修正的理论和计算公式见参考文献[13]。计算该大桥的竖向涡振位移最大幅值修正系数CV为1.572，对应扭转涡振最大幅值修正系数CT为2.028。弹性悬挂系统的竖向刚度采用8根等刚度的弹簧模拟；扭转刚度通过设置弹簧悬挂点距模型截面剪心顺风向间距0.174 m来模拟。模型安装完成后，实测节段模型竖向频率fh为4.172 Hz，扭转频率fα为4.300 Hz，与理论设计节段模型竖弯频率fv为4.160 Hz以及扭转频率ft为4.321 Hz分别相差0.29%和0.49%，满足试验要求。

由规范[14]计算的竖向涡振允许振幅为

[ha]=0.04/fv=0.04/0.416=0.096 2 m

(1)

扭转涡振允许振幅为

[θa]=4.56/Bft=4.56/(29×0.432)=0.364°

(2)

图4为模型试验结果换算到实桥的主梁振动幅值随风速变化曲线，从图4中可以看出，+3°攻角与0°攻角在低阻尼比(竖弯阻尼比为0.52%、扭转阻尼比为0.53%)下有明显的扭转涡激共振现象，此外，+3°攻角下主梁竖向幅值和扭转幅值从风速20 m/s开始就一直增大。在桥梁的风洞试验测试过程中，涡激振动对节段模型阻尼比的变化十分敏感，因此，首先把竖弯阻尼比提高到1.04%同时扭转阻尼比提高到0.96%，从图 4中可知，虽然没有观察到+3°攻角下幅值一直增大的现象，但+3°攻角和0°攻角依然存在明显的涡激共振现象，且+3°攻角下竖弯和扭转涡振幅值超过了规范限值，因此有必要通过气动措施来改善断面的气动性能。由于模型竖弯和扭转固有频率仅相差2.98%，竖弯和扭转涡振同时存在，同时消失，其具有明显的耦合特性。

(a) 竖向位移振动幅值风速曲线

(b) 扭转位移振动幅值风速曲线

通过对最大幅值位移时程做傅里叶变换，得到+3°与0°攻角在两种阻尼比下的幅值谱。从图 5中可以看出，在最大幅值的风速下，断面在每种工况下的竖弯和扭转涡激共振的频率是相同的，由此也可知不同于绝大部分桥梁断面竖弯和扭转涡激振动是相互独立的情况，该主梁断面的竖弯和扭转是耦合振动，至于竖弯和扭转涡激振动之间相互的影响有多大还有待进一步研究。从图 5中还可以发现竖弯和扭转涡激共振锁定频率都处在竖弯振动频率之前，和竖弯频率(图 5(b)图中靠前的虚竖线)很接近，也就是说扭转涡振频率没有真正意义上达到扭转固有频率，这和在后续加气动措施的情况下结论是一致的。因此，竖弯和扭转涡振相互耦合。从理论上来讲，扭转涡振最大振幅处的振动频率应该和扭转固有频率接近的。初步可以认为是由于竖弯频率比扭转频率稍低，当风速逐渐增大时，涡脱频率首先接近竖弯频率，然后发生锁定，恰好扭转固有频率处在竖弯涡振的锁定区间内，因此，当风速继续增大时，涡脱频率并没有增大，因而达不到扭转的固有频率，这抑制了扭转涡振振幅的增大，当风速再增大时，涡脱频率直接跳过了扭转固有频率，最后竖弯和扭转涡振振幅都减小，涡振现象消失。

(a) 竖向位移频谱图

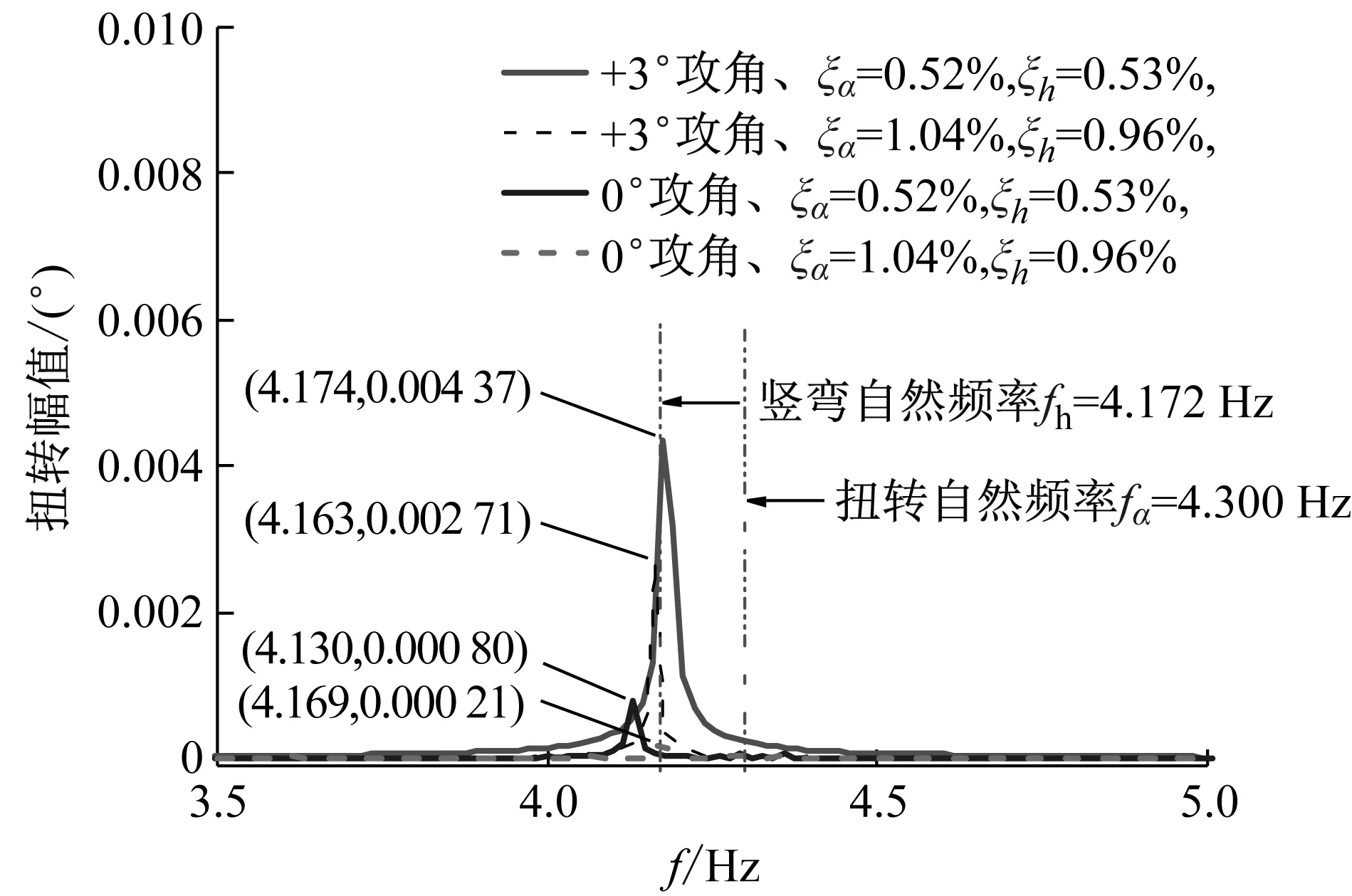
(b) 扭转位移频率图

发生耦合涡振时，竖向扭转振动的频率是一致的。为了研究耦合涡振时扭转和竖弯的相位差的演变特性，定义如下的相位差表达式

φ=(tαmax-thmax)ω

(3)

式中:φ为扭转和竖弯相位差；tαmax和thmax为相邻扭转和竖向峰值对应的时间；ω为竖弯和扭转耦合频率。

由于数据采集频率为200 Hz，式(3)算出来的相位差会产生±7.5°左右的误差。从图6中可以看出，0°攻角下扭转和竖弯相位差越接近对应响应幅值最大，+3°攻角下扭转和竖弯相位差为0的风速对应扭转涡振幅值最小。当来流风速大于20 m/s后，扭转和竖弯的相位差都减小。

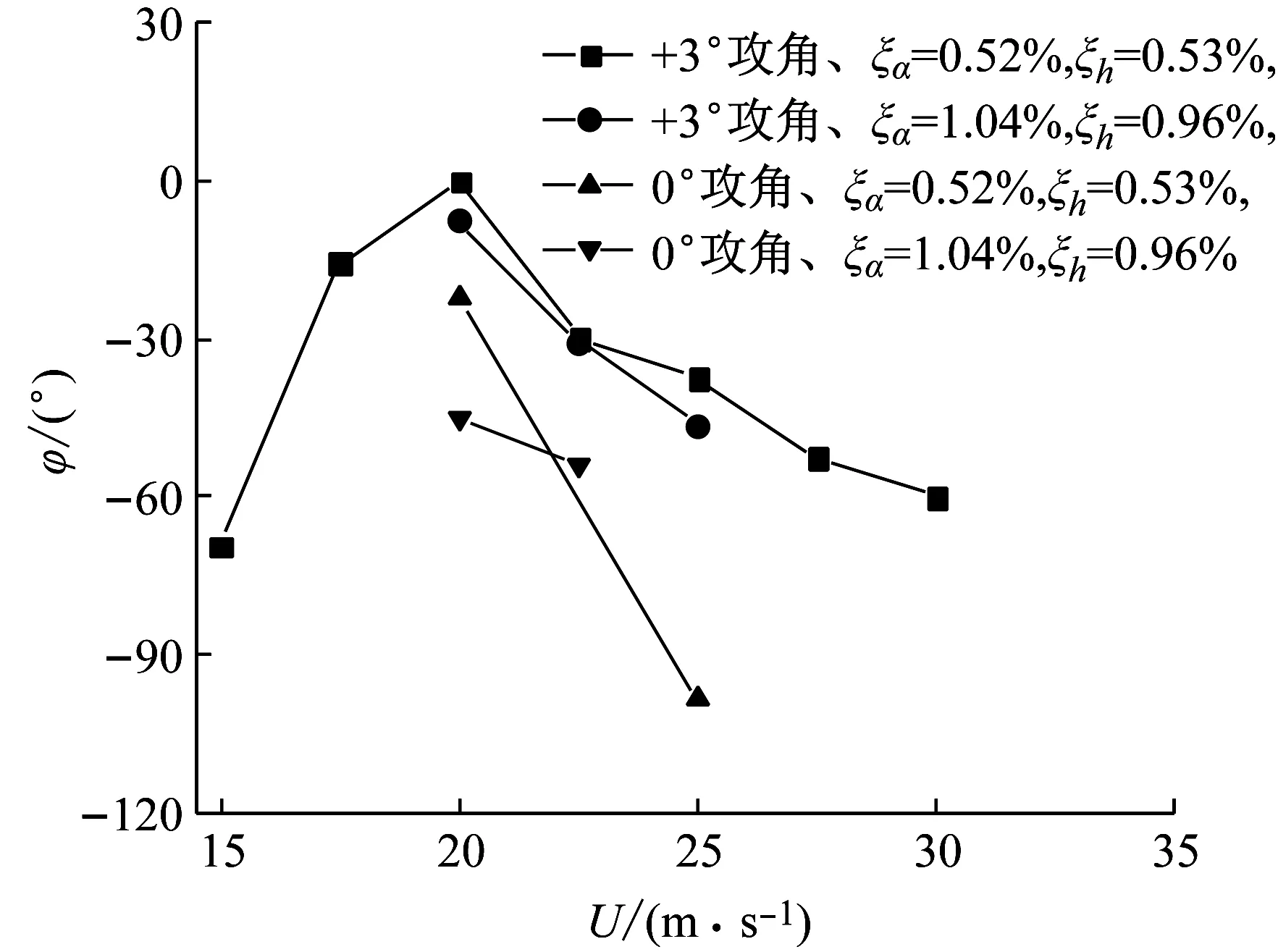
图6 扭转相对于竖向相位差

3 气动控制措施

针对主梁断面出现明显涡激共振的现象，通过试验测试设计了六种不同的减振措施方案如图7所示，相应的测试工况如表2所示。在所有减振措施方案中，试验条件均是在+3°攻角下且竖弯和扭转阻尼比分别为1.04%与0.96%。

图7 涡振气动措施示意图(m)

3.1 气动措施减振效果分析

在+3°攻角且来流为均匀流的情况下，相对于该桥的标准断面，涡振试验结果表明所有的气动措施方案均能降低涡振的幅值，具体如图8所示，其中工况三和工况四的减振效果最佳。工况四相对于工况三少了2道3.07 m高的下稳定板，且前者在涡振试验过程中基本观察不到明显的涡振且工程经济性也更好。比较工况二和工况三可以看出，下稳定板不透风的效果比透风的效果更佳，后者涡激共振现象不明显。工况三与工况五及工况四与工况六从抗风措施来看仅多了2道1.11 m高的上稳定板，反而引起了较大的涡振振幅，说明上稳定板在此断面并没有起到抑制涡振的作用。工况一相对于其它工况来说锁定区间最长，且在六种气动措施方案中控制涡振的效果是最差的，可见下导流板在此π型断面没能起到较好的控制效果。综合所有方案，工况三和工况四都能使竖向与扭转耦合涡振基本消失，而前一种有轻微扭转涡振现象的存在，同时后一种方案相对于前面一种方案的工程造价要低，因此在标准断面的基础上加上一道3.17 m高的下中央稳定板措施为最优的气动控制方案。同时也可以观察到所有工况中竖弯和扭转涡激共振并不是独立的而是相互影响的，它们同时存在，同时消失，这也间接的证明了竖弯和扭转涡激共振的频率的一致性。

表2 气动措施测试工况统计表

(a) 竖向振动位移幅值

(b) 扭转振动位移幅值

从图9中可以得知，施加气动措施的断面的竖弯和扭转涡振最大幅值处的振动频率是一致的， 而并没有出现竖弯和扭转振动频率不相同的情况，前面+3°和0°攻角下的标准断面也存在这种现象。所有幅值最大处的振动频率和竖向固有频率接近，仅相差在2.48%以内，这种偏差可能是试验测试点不够密及数据采集频率过低引起的。图8中的虚竖线表示模型的固有频率界线。

(a) 竖向位移频谱图

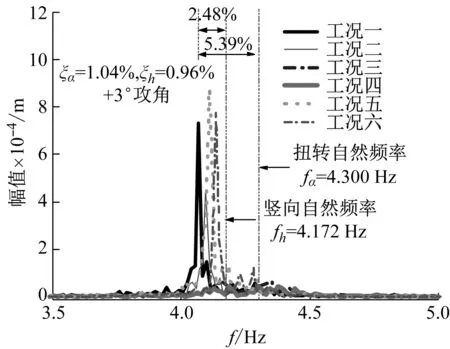
(b) 扭转位移频谱图

如图10所示，模型竖向固有频率和扭转固有频率仅相差2.97%。假使竖向涡激共振的锁定起始风速为4.500 m/s，根据涡脱频率与来流风速成线性的关系可知扭转涡振的锁定起始风速为4.638 m/s，仅比竖向涡振锁定起始风速大0.138 m/s。由此可知，扭转固有频率处于竖向涡激锁定区间内，因此标准断面及施加气动措施的试验观察不到扭转固有频率“锁定”现象的存在，这也证明了第2章中初步设想。

图10 结构涡激共振的“锁定”现象

3.2 作用效果评价

为了评价气动措施对π型叠合梁断面弯扭耦合涡振的控制效果。本文定义了用于评价气动措施控制效果指标最大幅值抑制率ξ，其表达式定义如式(4)

(4)

式中,Amp0、Amp分别为原始断面涡振最大幅值和施加了气动措施的最大幅值。对于完全抑制到的气动措施，上述的抑制率取1。

从工程实际来看，抑制率大于零则表示该措施有一定的抑制作用。如图11中所示，工况四的气动措施控制效果最好，竖弯和扭转的抑制率分别达97.9%和97.5%。竖弯涡激共振和扭转涡激共振的幅值抑制率基本一致，可以看出气动措施对竖弯和扭转涡振抑制的机理是相同的，也就是说竖弯和扭转涡激共振是由同一个振动频率驱动。从图 8中也可以看出竖向和扭转的幅值随风速演变规律基本一致，进一步验证了此π型断面是竖弯和扭转耦合涡激共振。

图11 气动控制措施最大涡振幅值抑制效率

4 结 论

通过对某π型开口断面斜拉桥主梁刚性节段模型进行风洞试验，本文系统研究了该断面成桥状态的涡振性能。研究结果表明该桥在不采取任何抗风措施的条件下，主梁断面出现了明显弯扭耦合涡激振动现象，通过采取设计下中央稳定板措施，达到了抑制该桥耦合涡激振动的目的，主要结论如下：

(1) 本文的研究再次表明，开口断面桥梁容易出现大幅涡激共振。本文研究的桥梁断面在+3°攻角下出现明显扭转涡激振动，且幅值超过规范允许值。

(2) 所有气动措施方案中，单独加3.17 m高下中央稳定板的方案是最优的，竖弯和扭转的涡振最大振幅的抑制率分别达97.9%与97.5%，基本消除了涡激共振。结合已有的文献，本文的研究再次表明中央稳定板是一种有效的气动减振措施。

(3) 所有方案的竖弯和扭转涡激共振的频率一致，即竖弯和扭转耦合涡激共振，且振动的频率锁定在竖向固有频率附近；气动措施对竖弯和扭转涡激振动抑制的机理相同；竖向和扭转涡振幅值随风速演变的规律一致，都由同一个振动频率驱动。