一个具有多翼吸引子的四维多稳态超混沌系统

鲜永菊， 扶坤荣， 徐昌彪,2

(1.重庆邮电大学 通信与信息工程学院，重庆 400065； 2.重庆邮电大学 光电工程学院，重庆 400065)

混沌是非线性系统所特有的一种现象，表现出丰富的动力学行为，在信息、生物、经济等领域有广泛的应用前景，近年来已成为人们研究的热点[1-5]。

混沌系统中的多稳态是指系统在给定参数下存在两个或多个吸引子共存，反映了系统的状态多样性[6-8]。混沌系统中的多翼即为吸引子具有两个或多个翅膀，体现了系统的结构多样性[9-11]。显然，存在多翼吸引子的多稳态混沌系统表现出更加复杂的动力学行为，具有更为重要的理论研究意义和工程应用价值[12-15]。譬如，把这种系统应用于信息加密时，密钥的选取可以基于多稳态下的不同吸引子，也可以基于不同参数取值下的不同吸引子或者多翼吸引子中的不同翅膀，从而使系统获得更好的保密性能[16]。

目前，只有少量文献报道了具有多翼吸引子的四维多稳态混沌系统。Lai等[17]通过引入Signum函数，构造了一个具有至少7种吸引子共存类型(不同运动状态和拓扑结构的吸引子共存视为不同类型)的四维混沌系统。随着参数的变化，四翼混沌吸引子可分解为两个共存的双翼混沌吸引子。Zhang等[18]提出了一个具有至少10种吸引子共存类型的四维混沌系统。随着参数的变化，此系统可以产生从单翼到四翼的混沌吸引子。

本文构造了一个只有1个平衡点的四维超混沌系统，此系统具有至少12种吸引子共存类型。在多组参数值下，系统均存在不同类型的吸引子共存，譬如：两个周期吸引共存，周期与拟周期吸引子共存，双翼混沌与超混沌吸引子共存，两个双翼混沌吸引子共存，双翼与四翼混沌吸引子共存，两个双翼超混沌吸引子共存，两个双翼拟周期吸引子共存，两个双翼超混沌、四翼混沌、四翼超混沌等四个吸引子共存。特别地，在给定参数值下，四翼超混沌吸引子可分解为两个共存的双翼超混沌吸引子。

1 系统模型与基本特性分析

1.1 系统模型

系统的数学模型如式(1)所示。其中，x，y，z，w为系统状态变量，a，b，c，d为系统参数。取a=6，b=4，c=8，d=2，初始值为[1,2,3,4]时，系统存在一个典型的四翼蝶形超混沌吸引子，如图1所示。此时系统的四个Lyapunov指数(LE)为1.657，0.117，0，-37.324。显然，系统有两个正的Lyapunov指数，表明其为一个超混沌系统。Lyapunov维数DL=3+(LE1+LE2+LE3)/|LE4|=3.048，即为分数维，从而验证了系统是分形的。

(a) x-y

(b) x-z

(c) x-w

(d) y-z

(1)

1.2 平衡点及其稳定性

令非线性方程(1)的左边等于0，即

(2)

求解方程可得唯一平衡点，即S0=(0,0,0,0)。在平衡点处线性化系统，得其Jacobi矩阵为

(3)

令det(λI-J)=0，得到多项式

f(λ)=λ4+(a-c)λ3+(-ac+d)λ2+adλ

(4)

1.3 时域波形图和Poincaré截面

取a=6，b=4，c=8，d=2，初始值为[1,2,3,4]时，采用四阶龙格-库塔算法对式(1)进行求解，可得x的时序图，如图2所示。显然，系统作非周期运动。z=0上的Poincaré截面如图3所示。可以看出，Poincaré截面上形成了具有分形结构的密集点，表明了图1所示的四翼超混沌吸引子的存在。

图2 状态变量x的时序图

图3 z=0上系统的Poincaré截面

1.4 Lyapunov指数

取b=4，c=8，d=2，初始值为[1,2,3,4]时，Lyapunov指数和x随a变化的分岔图分别如图4(a)和图5(a)所示。可知，a由0增加到10时，系统运动状态变化过程为：周期→拟周期→混沌→超混沌→混沌。

取a=6，c=8，d=2，初始值为[1,2,3,4]时，Lyapunov指数和x随b变化的分岔图分别如图4(b)和图5(b)所示。可知，b由0增加到20时，系统运动状态变化过程为：混沌→超混沌→混沌→拟周期→周期。

取a=6，b=4，d=2，初始值为[1,2,3,4]时，Lyapunov指数和y随c变化的分岔图分别如图4(c)和图5(c)所示。可知，c由0增加到30时，系统运动状态变化过程为：周期→拟周期→混沌→超混沌→混沌。

(a) 参数a变化

(b) 参数b变化

(c) 参数c变化

(d) 参数d变化

(a) 参数a变化

(b) 参数b变化

(c) 参数c变化

(d) 参数d变化

取a=6，b=4，c=8，初始值为[1,2,3,4]时，Lyapunov指数和x随d变化的分岔图分别如图4(d)和图5(d)所示。可知，d由0增加到30时，系统运动状态变化过程为：混沌→超混沌→混沌。

2 多稳态特性和多翼拓扑结构

2.1 多稳态特性

情形1：参数a变化

取a∈[0,5]，b=4，c=8，d=2，初始值为[1,±2,3,4]时，x随a变化的分岔图如图6(a)所示。可知，随着a的变化，系统存在多种类型的吸引子共存：当a=2时，两个周期吸引子共存；当a=2.9时，拟周期和周期吸引子共存；当a=3.2时，两个混沌吸引子共存。Lyapunov指数如表1所示，x-y平面相图如图7(a)～图7(c)所示，表明当a∈[0,5]时系统的多稳态特性由x来体现。

(a) a∈[0,5]

(b) a∈[8.8,10]

(a) a=2

(b) a=2.9

(c) a=3.2

(e) a=8.9

取a∈[8.8,10]，b=4，c=8，d=2，初始值为[1,2,±3,4]时，z随a变化的分岔图如图6(b)所示。可知，随着a的变化，系统存在多种类型的吸引子共存：当a=10时，两个双翼混沌吸引子共存；当a=8.9时，双翼混沌和四翼混沌吸引子共存。Lyapunov指数如表1所示，共存吸引子如图7(d)～图7(e)所示，表明当a∈[8.8,10]时系统的多稳态特性由z来体现。

情形2：参数b变化

取b∈[9,18]，a=6，c=8，d=2，初始值为[±1,2,3,4]时，x随b变化的分岔图如图8(a)所示。可知，随着b的变化，系统存在多种类型的吸引子共存：当b=9.9时，两个超混沌吸引子共存；当b=14时，两个拟周期吸引子共存；当b=18时，两个周期吸引子共存。Lyapunov指数如表1所示，x-y平面相图如图8(b)～图8(d)所示，表明当b∈[9,18]时系统的多稳态特性由x来体现。

(a) 分岔图

(b) b=9.9的共存吸引子

(c) b=14的共存吸引子

(d) b=18的共存吸引子

情形3：参数c变化

取c∈[0,4]，a=6，b=4，d=2，初始值为[1,±2,3,4]时，y随c变化的分岔图如图9(a)所示。可知，随着c的变化，系统存在多种类型的吸引子共存：当c=0.4时，两个周期吸引子共存；当c=1.25时，两个拟周期吸引子共存；当c=2时，两个混沌吸引子共存。Lyapunov指数如表1所示，y-z平面相图如图9(b)～图9(d)所示，表明当c∈[0,4]时系统的多稳态特性由y来体现。

情形4：参数a=6，b=4，d=2，c=21

取a=6，b=4，c=21，d=2，初始值为[±1,2,3,4]、[1,-2,3,4]和[-1,2,-3,4]，有2个孤立的双翼超混沌吸引子、1个四翼蝶形超混沌吸引子和1个四翼蝶形混沌吸引子共存。Lyapunov指数如表1所示，相图和时序图分别如图10(a)～图10(c)所示，表明了共存吸引子的存在，且系统的多稳态特性由x来体现。

(a) 分岔图

(b) c=0.4的共存吸引子

(c) c=1.25的共存吸引子

(d) c=2的共存吸引子

(a) [1,2,3,4]和[-1,2,-3,4]

(b) [-1,2,3,4]

(c) [1,-2,3,4]

2.2 多翼拓扑结构

情形1：相同参数取值，不同初始值下的多翼变化

如图10(a)～图10(c)所示，在同一组参数取值下，取不同的初始值时，系统的四翼蝶形超混沌吸引子可以分解为两个孤立的双翼超混沌吸引子，也可以演变为一个四翼蝶形混沌吸引子。

表1 不同参数和初始值下的共存吸引子

情形2：相同初始值，不同参数取值下的多翼变化

初始值取[1,2,3,4]，固定a=6，c=8，d=2，b的取值由10.1→8→6→1.45时，系统行为的演变过程为：双翼混沌吸引子→双翼超混沌吸引子→四翼蝶形超混沌吸引子→四翼蝶形混沌吸引子。相图如图11(a)～图11(d)所示，Lyapunov指数如表2所示。可知，在初始值相同时，取不同的参数值，系统出现处于不同运动状态的双翼吸引子和四翼蝶形吸引子。

(a) b=10.1 (b) b=8 (c) b=6 (d) b=1.45

表2 不同参数下的吸引子拓扑结构

3 系统的电路仿真

3.1 模拟电路仿真

利用Multisim电路仿真软件，采用线性电阻、电容、LM2924N运算放大器、AD633模拟乘法器，实现混沌系统的电路设计与模拟。根据系统的动力学方程，设计电路原理图如图12所示，其中乘法器的输出增益为0.1。改变不同电容和电阻的值，以实现耗散超混沌系统电路的模拟。根据电路原理图以及电路理论，得自激振荡电路方程如式(5)所示。其中R1～R15为线性电阻，C1～C4为电容。取电容C1=C2=C3=C4=1 μF，电阻R7=R8=R11=R12=R14=R15=1 kΩ。

(5)

当a=6，b=4，c=8，d=2时，对比式(1)和式(5)，可以得到电阻值如式(6)。根据初始值[1,2,3,4]，可得Vx=1，Vy=2，Vz=3，Vw=4。仿真结果如图13所示，表明模拟电路仿真结果与数值仿真结果一致。

(6)

图12 电路原理图

(a) x-y

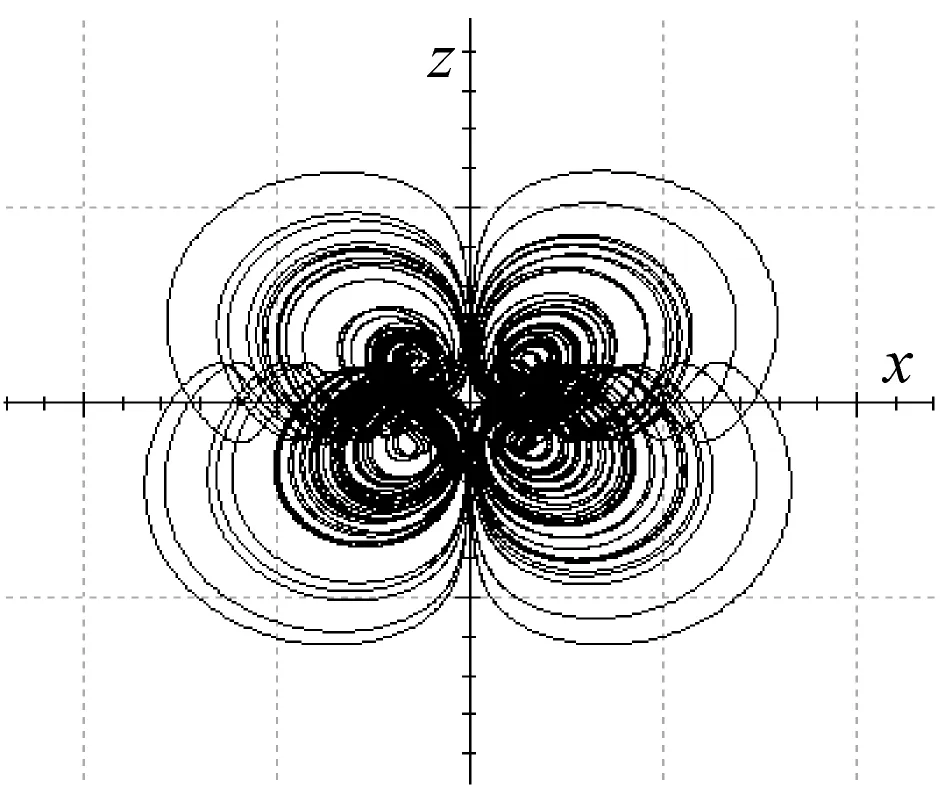
(b) x-z

(c) x-w

(d) y-z

3.2 数字电路仿真

由于模拟器件的性能容易受到环境温度、湿度以及器件老化的影响，故模拟电路实现混沌系统会严重影响系统的动力学特性，限制了模拟混沌电路在工程中的应用。采用FPGA数字电路技术实现混沌系统可以很好地避免这些问题，保证了混沌吸引子的稳定可靠。由于系统是一个连续时间系统，FPGA无法直接处理，本文采用Euler算法将系统(1)离散化，得到的差分方程为

(7)

式中:a=6，b=4，c=8，d=2;迭代步长Δt=0.001。

Xilinx RTL原理图如图14所示，FPGA硬件及其实验效果如图15所示。当初始值为[1,2,3,4]时，由示波器随机捕获的系统相位图如图16所示。可知，数字电路仿真结果与模拟电路仿真以及数值仿真结果一致。

图14 Xilinx RTL原理图

图15 FPGA硬件及其实验效果

(a) x-y

(b) x-z

(c) x-w

(d) y-z

4 系统复杂度分析及超混沌序列的随机性测试

4.1 系统复杂度分析

复杂度测度是描述混沌系统复杂行为的一种重要方法。混沌系统的复杂度是指采用相关算法衡量混沌序列接近随机序列的程度。复杂度值越大，序列越接近随机序列[19]。

混沌序列的复杂度分为行为复杂度和结构复杂度，前者测量短时间窗口内序列产生新模式的概率大小，后者通过变换域内的频率特性和能量谱特性来分析序列的复杂程度。与行为复杂性相比，结构复杂性具有全局统计意义，因为其针对的是序列的全部而不是局部。目前评价结构复杂度的算法主要有谱熵(SE)算法和C0算法。

以a和b为变量，初始值为[1,2,3,4]时系统随参数变化的谱熵(SE)复杂度和C0复杂度分别如图17和图18所示。

(a) 参数a

(b) 参数b

(1) 参数a变化，b=4，c=8，d=2时，系统运动状态从周期变到拟周期，SE和C0较小；从拟周期向混沌、超混沌状态转变时，SE和C0逐渐增加到最高值；维持超混沌状态时，SE和C0在最高值附近波动；最终系统处于混沌状态时，SE和C0减小至较高值。

(a) 参数a

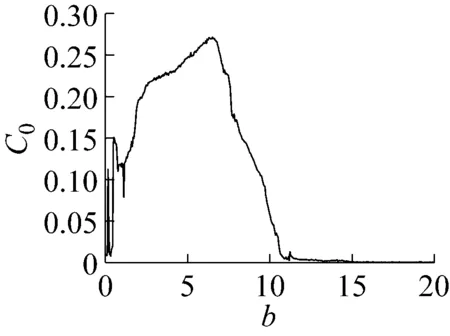
(b) 参数b

(2) 参数b变化，a=6，c=8，d=2时，系统运动状态从混沌变到超混沌状态时，SE和C0由较高值上升到最高值；从超混沌变到混沌状态时，SE和C0逐渐减小至较高值；从混沌逐渐变到拟周期、周期状态时，SE和C0进一步减小，最终维持在一个较低值。

4.2 超混沌序列的随机性测试

取a=6，b=4，c=8，d=2，初始值为[1,2,3,4]时，采用四阶龙格-库塔法求解系统得到超混沌序列。利用美国国家标准技术研究所(NIST)的SP800-22 Revla的15种测试方法[20]检验此超混沌序列的随机特性(P-value≥0.01表示测试的比特序列是随机的，否则认为序列是非随机的)，测试结果如表3所示。可知，超混沌序列通过了15项随机测试。

表3 基于SP800-22 Revla的15项测试结果

5 结 论

本文构建了一个新型的四维超混沌系统，数值分析了系统的基本动力学特性，仿真了系统的模拟电路和数字电路，探讨了系统的动态复杂度，测试了系统超混沌序列的随机性，得出如结论：

(1) 系统只有一个平衡点，且为不稳定平衡点。

(2) 系统表现出丰富的多稳态特性，即在多组参数值下，系统均存在不同类型的吸引子共存，譬如：两个周期吸引共存，周期与拟周期吸引子共存，双翼混沌与超混沌吸引子共存，两个双翼混沌吸引子共存，双翼与四翼混沌吸引子共存，两个双翼超混沌吸引子共存，两个双翼拟周期吸引子共存，两个双翼超混沌、四翼混沌、四翼超混沌等四个吸引子共存。

(3) 在给定参数值下，四翼超混沌吸引子可分解为两个共存的双翼超混沌吸引子。

(4) 数字电路和模拟电路的仿真结果均与数值分析结果一致，表明了系统的可实现性。

(5) 在混沌和超混沌状态下系统复杂度高，且超混沌序列通过了SP800-22 Revla的15项随机测试。