翼型凹变对风轮旋转噪声影响特性分析
2021-01-16吕文春汪建文段亚范马剑龙孟克其劳陈金霞
吕文春, 汪建文, 段亚范, 马剑龙, 孟克其劳, 陈金霞
(1.内蒙古工业大学 能源与动力工程学院,呼和浩特 010051;2.内蒙古机电职业技术学院 科技与职教研究中心,呼和浩特 010070;3.内蒙古自治区高等学校 可再生能源工程研究中心,呼和浩特 010051;4.风能太阳能利用技术教育部重点实验室,呼和浩特 010051)
随着分散式风电的快速发展,越来越多的风力机安装在离负荷中心区域较近且风能密度较高的地区。然而风力机在运行中产生的噪声问题则严重影响了当地居民的正常生活,成为阻碍分散式风电发展的一个重要因素。风力机在运行中的噪声主要分为机械噪声和气动噪声,其中机械噪声已经得到很好的控制。因此,如何降低风力机的气动噪声问题则变的尤为重要。
目前,国内外学者为解决风力机的气动噪声问题进行了大量研究。其中,研究的方向多集中在叶片翼型自噪声和旋转噪声等方面。翼型自噪声主要包含尾缘噪声、失速噪声和层流涡噪声等[1]。其中,对于尾缘噪声的研究相对较多。尾缘噪声是由叶片表面的湍流边界层流经尾缘并相互作用而产生[2]。因此,针对尾缘噪声常用的降噪方法就是控制叶片吸力面湍流边界层的生成或对翼型尾缘进行结构优化等。而对于湍流边界层的控制,主要是通过扰流实验探究湍流强度、攻角及来流雷诺数等对湍流边界层生成的影响[3-5],并通过改变翼型厚度或在吸力面采用抽吸孔、脊状结构及添加粗糙元等方式延迟翼型吸力面湍流边界层的生成[6-8]。相关典型研究有:王松岭等通过在翼型吸力面增加脊状结构有效改善边界层分离状况,并减小了翼型表面的压力脉动;Jelinek等探究了平面粗糙元对边界层的转捩现象的影响。对于叶片尾缘结构优化方面,主要是通过改变叶片尾缘的形状从而破坏脱落涡结构,起到降噪效果。目前对尾缘的结构优化方式有很多种,比如锯齿状、波浪形,钝尾缘或添加襟翼等[9-12]。典型研究有:Arce Leon等探究了锯齿尾缘对叶片气动噪声的影响;苏彩虹发现波浪形尾缘可以有效降低叶片的宽频噪声。
在风轮旋转噪声方面,风轮旋转噪声是由于叶片经过流体时产生周期性涨缩作用和叶片上载荷力的作用形成,且噪声频率与风轮转速相关[13]。相关研究有:Wasala等[14]发现水平轴风力机风轮旋转产生的噪声为主要噪声,且声压级较高;李运志等[15]发现风轮的旋转噪声频率主要集中在200 Hz以下,并确定了声源位置。陆贇韬[16]发现旋转噪声的强度与叶片对流场的扰动有关,随着振动幅值的增大而增强。
综合国内外文献可知,目前对风力机气动噪声的降噪方法多集中在翼型自噪声方面,而针对风轮旋转噪声的降噪方法研究还相对较少。在以往研究中发现翼型凹变可以提升叶片的结构特性并且有效延迟叶片吸力面气流的转捩位置,提高叶片的气动性能[17],然而翼型凹变对风轮气动噪声的影响以及影响原因还未揭示。因此,本文针对声压级较高的旋转噪声进行分析,探究了翼型凹变对风轮旋转噪声的影响。并从结构场出发解析了翼型凹变对风轮旋转噪声影响的原因。
1 旋转噪声测试及分析
1.1 测试系统及方法
测试对象为某S翼型水平轴风力机三叶片风轮,风轮直径为1.4 m。实验在内蒙古工业大学B1/K2式风洞开口实验段进行,声数据的采集及处理由B&K公司的60通道圆形声阵列系统完成。其中,声阵列直径为0.78 m,传声器的灵敏度为12.5 mV/Pa,测量范围为10~20 000 Hz。风轮转速通过直流电子负载调节,其精度为0.1%+0.1%FS,并利用Fluke实时监测功率和转速等参数。在测试中,声阵列盘平行风轮放置,并放置在风轮下风向的后方0.2 m处,实验采用SONAH算法进行处理分析,测试设备安装如图1所示。

图1 测试设备安装图
1.2 凹变叶片形式确定
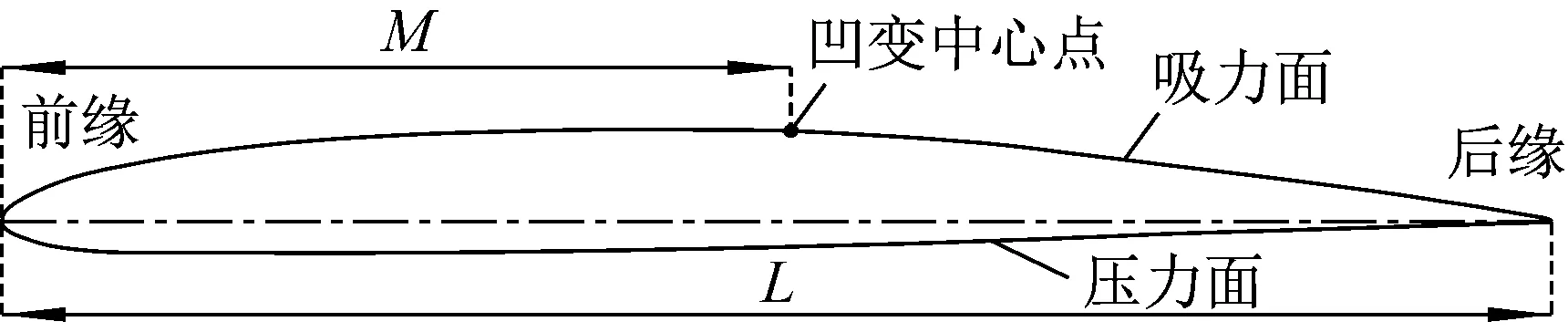
翼型凹变叶片是在原翼型的基础上,通过翼型绕流实验确定吸力面的转捩位置而进行凹变得到。凹变的方式及长度则通过功率实验确定。经过测试发现凹变位置在其吸力面0.8倍弦长处,凹槽长度为350 mm时风轮输出功率最高[18]。以图2(a)中某翼型为例,假设流动的分离点常常出现在M处,则选定M处为翼型凹变中心。考虑到翼型弦长显著大于其最大厚度,尝试将翼型凹变的几何结构采用椭圆形。
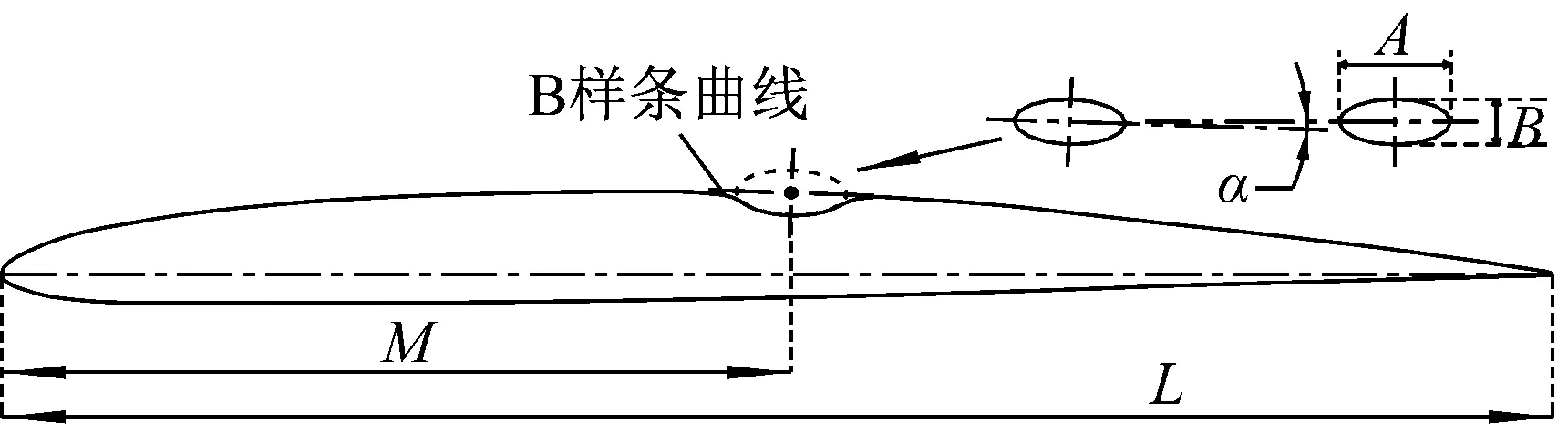
令椭圆中心为M位置,椭圆长轴为弦长的7.2%、短轴为弦长的3.6%,并使椭圆长轴与M处原翼型曲线相切,凹变部分与非凹变部分之间采用样条曲线连接,具体过程如图2(b)所示。
(a) 原翼型
(b) 凹变翼型
图2中:L为翼型弦长;M为凹变中心点到翼型前缘点的距离;A为椭圆长轴;B为椭圆短轴。
原翼型叶片和翼型凹变叶片实物如图3所示(其中原翼型叶片表示为A,翼型凹变叶片表示为B)。
1.3 对旋转噪声测试结果分析
1.3.1 背景噪声分析
声信号在测量中有包括风洞运行在内的环境背景噪声,会对风轮旋转噪声的准确获取产生干扰,因此在测试前需进行背景噪声测试。背景噪声测试中,不安装风力机,阵列盘的测量位置与安装风力机的测试位置相同。

图3 叶片实拍图
风轮的旋转噪声采用SONAH算法进行分析,声信号处理中不做常规计权处理,并在处理过程中采用恒定频域(1 Hz)分析,以确保达到细化频谱的目的。
以来流风速为9 m/s为例,近场背景噪声测试如图4所示。由图4可知,风洞在低频(200 Hz)以内的主要噪声是由风洞入口处轴流式引风机叶片的旋转噪声(77 Hz)及其谐波构成。
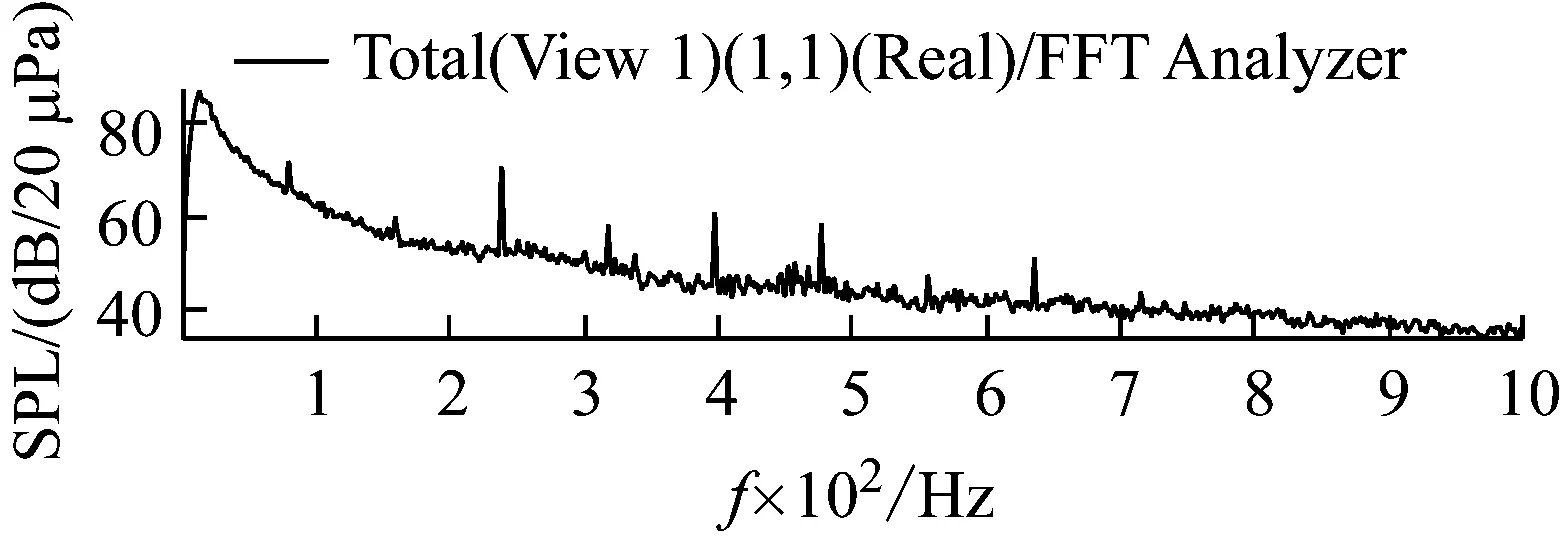
图4 近场背景声频谱分布图
1.3.2 对旋转噪声分析
以风速为9 m/s,转速为600 r/min的工况为例,得到风轮旋转噪声声压级频谱图,如图5所示(其中f为旋转基频,2f为旋转2倍频,3f为旋转3倍频,4f为旋转4倍频)。
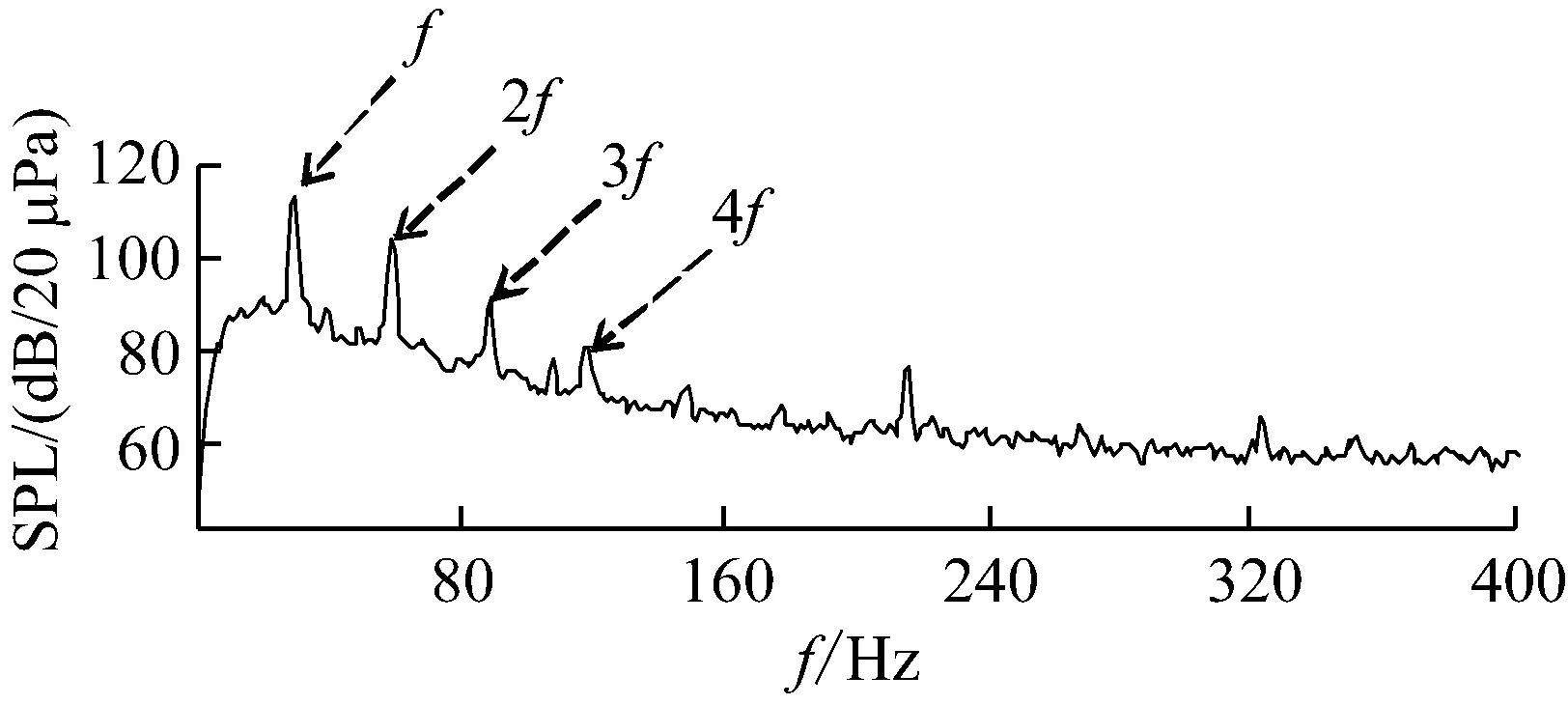
(a) A 叶片
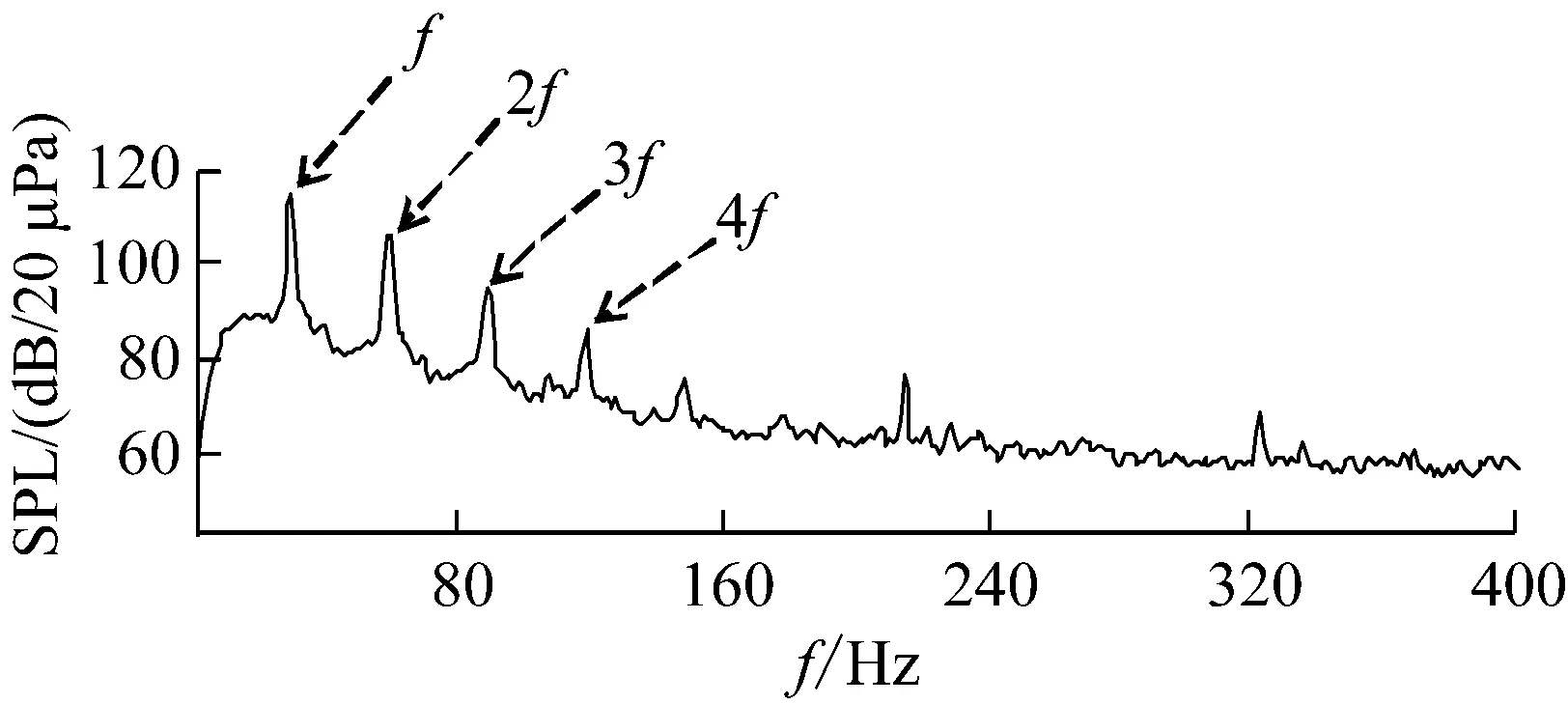
(b) B 叶片
通过对图5分析发现,旋转噪声主要由基频及其倍频谐波组成,且频率主要位于200 Hz以内。另外,在声频谱图中除旋转噪声外还有其它噪声峰值,通过声源识别发现此处的噪声峰值为电机机舱噪声,因此不对其进行分析。
为了探究翼型凹变对旋转基频及其倍频谐波声压级的影响,本文提取不同工况下倍频谐波的声压级进行分析,如表1、2所示(以转速600 r/min和风速9 m/s为例)。
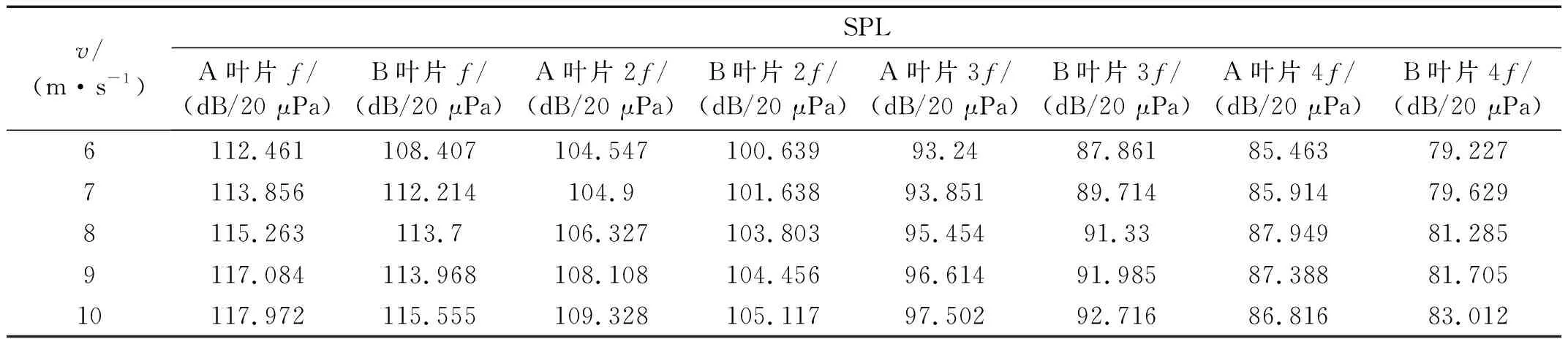
表1 风速变化对叶片旋转噪声的影响
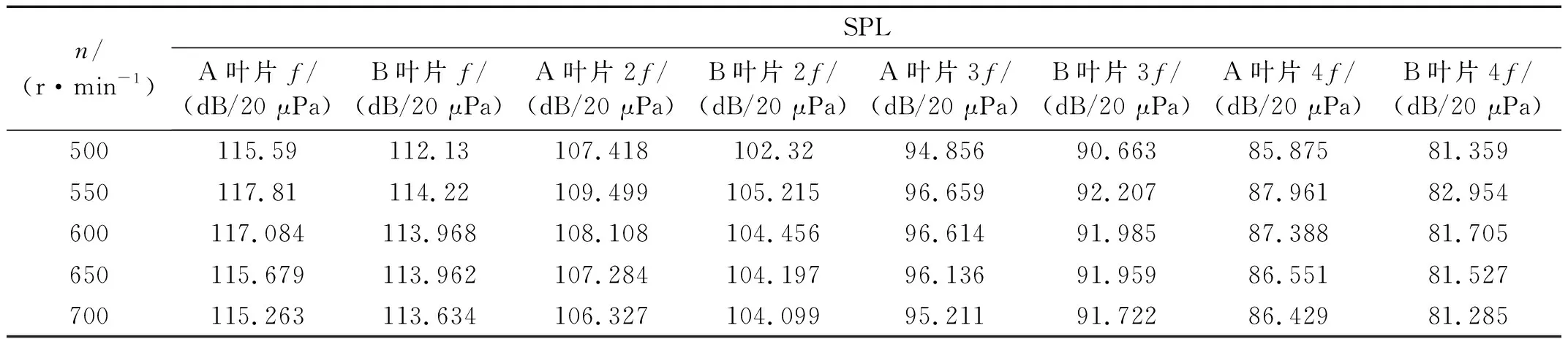
表2 转速变化对叶片旋转噪声的影响
通过对叶片旋转噪声随工况变化分布表分析发现,在相同工况时,B叶片旋转噪声的声压级均明显低于A叶片,说明翼型凹变后可以明显降低叶片的旋转噪声。另外发现,旋转基频的噪声声压级最大,其倍频声压级随着倍频次数的增加而逐渐减小。同时,当转速相同时,旋转噪声的声压级随着风速的增加而逐渐增大,而当风速相同时,旋转噪声的声压级随着转速的增加呈现出先升高后降低的趋势。
为了探究在相同工况下,翼型凹变对叶片旋转基频及其倍频噪声的影响变化。本文以式(1)来表示在相同工作条件下,翼型凹变引起声压级的变化值。
φi=SPLA叶片,i-SPLB叶片,i
(1)
其中(i=1、2、3、4)分别表示旋转基频和第二、三和四次倍频谐波。为了分析翼型凹变对不同倍频谐波声压级影响的敏感性,本文在相同工况下用式(2)定义参数ψ,如图6所示(以风速9 m/s,转速600 r/min为例)。
(2)
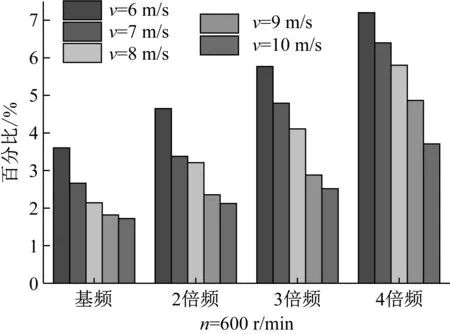
(a) 风速变化对不同倍频声压级的敏感性影响
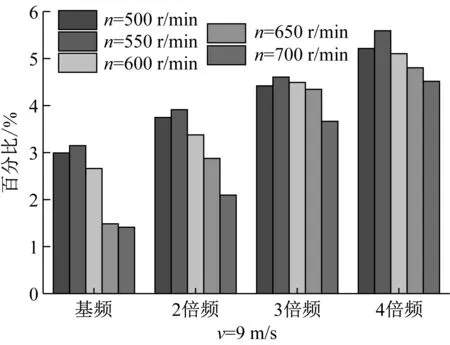
(b) 转速变化对不同倍频声压级的敏感性影响
通过对图6分析发现,在相同工况下,翼型凹变对叶片不同倍频谐波噪声的敏感性随着倍频次数的增加而逐渐增强,最高可达7.2%。另外,当转速相同时,翼型凹变对不同倍频谐波噪声的敏感性随着风速的增加而逐渐减弱。而当风速相同时,翼型凹变对叶片不同倍频谐波噪声的敏感性随着转速的增加呈现出先增强后减弱的趋势,且当n=550 r/min时,翼型凹变对叶片不同倍频谐波噪声影响的敏感性最强。
通过以上分析发现,不同倍频谐波噪声受翼型凹变影响的变化趋势相似,只是影响的敏感性不同。由于在叶片旋转噪声中旋转基频噪声的声压级最高,因此本文重点对叶片旋转基频噪声进行分析。
1.3.3 对旋转基频噪声分析
以风速为8 m/s、9 m/s、10 m/s和转速600 r/min、650 r/min、700 r/min等工况为例,对其旋转基频噪声进行分析,如图7所示。
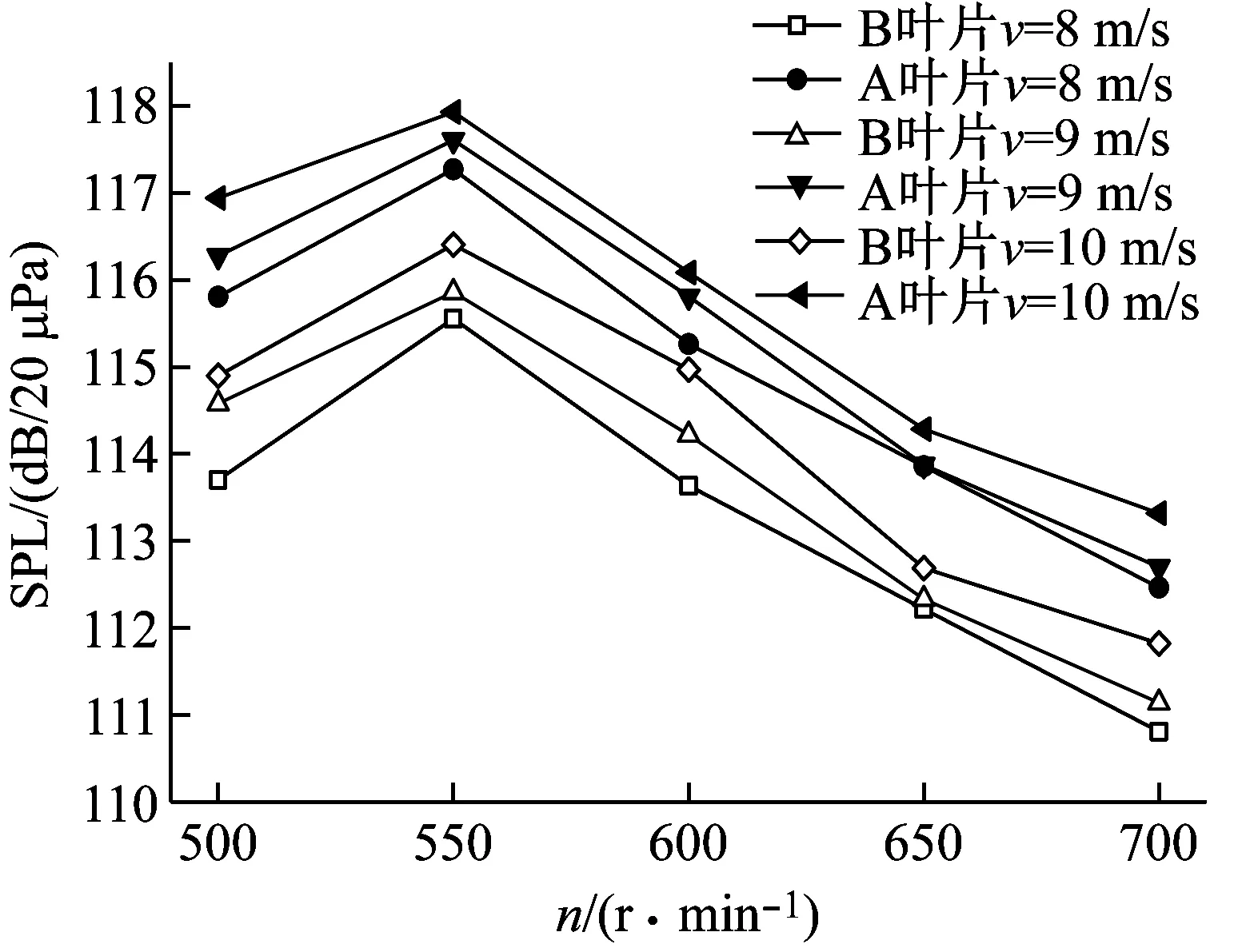
(a) 风速变化对叶片旋转基频噪声的影响
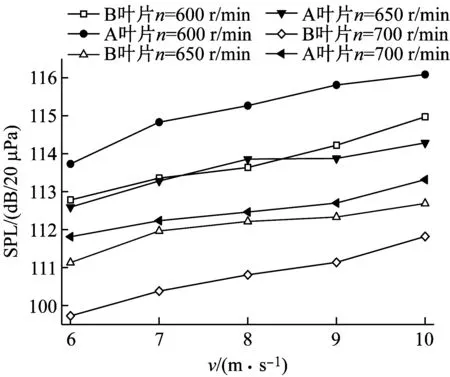
(b) 转速变化对叶片旋转基频噪声的影响
通过对图7分析发现,翼型凹变后只是降低了旋转基频噪声的声压级,却没有改变旋转基频噪声随工况的变化趋势。即当风速相同时,旋转基频噪声的声压级随着转速的增加呈现先升高后降低的趋势,且峰值均出现在转速为550 r/min的工况处,而当转速超过550 r/min时声压级逐渐降低。分析原因发现,此刻风轮受离心钢化作用影响明显,导致叶片刚度增加从而减弱了叶片受气动载荷的影响。同时,在相同转速下叶片的旋转基频噪声的声压级随着风速的增加而逐渐增大,说明风轮旋转基频噪声与气动载荷之间呈正相关性。
2 对风轮旋转噪声降低原因分析
风轮的旋转噪声是由于风轮与周期性来流相互作用以及对表面流体的涨缩作用而产生。因此,本文从结构场出发,分别对原叶片和凹变叶片进行结构动态测试,并通过分析翼型凹变对风轮叶片刚度及动频的影响,探究了翼型凹变降低风轮旋转噪声的原因。
2.1 翼型凹变对刚度的影响
2.1.1 测试系统及方法
测试系统采用B&K公司研发的PULSE结构振动分析系统,该系统的最大误差不超过2.8%。测量时,在叶片压力面两侧均匀布置8个单向加速度传感器。测试方法采用瞬态激振法,单点激励,多点响应。振动频率采集范围设置为0~400 Hz。加速度传感器的布置方式及激励点如图8所示。
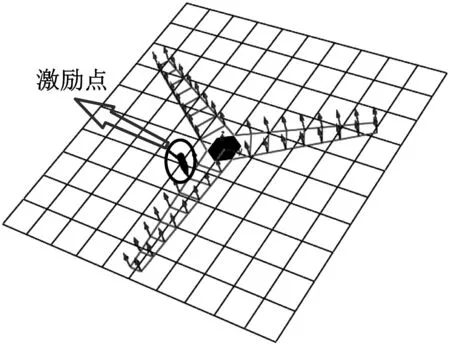
图8 风轮刚度测试模型图
2.1.2 风轮刚度测试结果分析
将数据导出到Reflect中进行后处理分析得到A叶片与B叶片所对应各阶的振动频率及阻尼比,如表3所示。

表3 风轮振动固有频率及阻尼比
从表3中可以得出,B叶片较于A叶片在轴向窜动、一阶反对称、一阶对称的固有频率分别有1.16%、1.45%和0.48%的增加。分析其原因:当叶片被力锤敲击时的振动形式,可以看做为一个单自由度有阻尼的振动形式。
则叶片的固有频率
(3)
式中:f为固有频率;k、m为刚度与质量;ζ为阻尼比。
则叶片静刚度
(4)
通过对叶片称重发现,翼型凹变后叶片质量减少了1%,由表3可知,翼型凹变后叶片的固有频率和阻尼比都得到较大的提升。因此,翼型凹变后可以有效的增加叶片的静刚度。另外发现,翼型凹变后叶片轴向窜动和一阶振动阻尼比的提高使得叶片振动消减速度变快,即在相同工况下翼型凹变叶片的疲劳损失也会有一定程度的下降。
2.2 翼型凹变对风轮动频的影响
2.2.1 测试方法和传感器测试点分布
测试方法采用布置于发电机前端部靠近风轮处的加速度传感器捕获振动频谱,通过已获得的模态数据结合谱分析法识别风轮动频,传感器布置如图9所示。
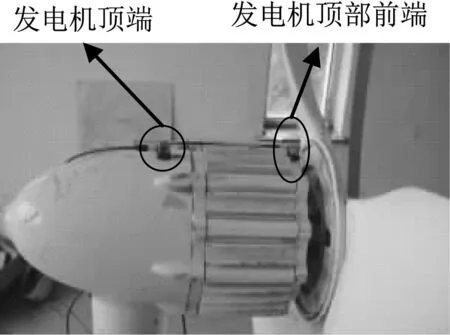
图9 传感器布置
2.2.2 动频识别
通过对2个不同位置的传感器动态频谱图分析发现,布置在发电机顶部前端的1号传感器的振动频谱与模态频谱有很好的相似性,只是各型振动加速度值和频率有所差异,这是由于风轮在旋转时受气动载荷和离心力的影响所致。因此,本文主要以1号传感器捕获的振动频谱为基础进行分析,探究翼型凹变对风轮叶片振动特性的影响。
提取不同工况下,A和B叶片的结构振动响应频谱,并依据模态频率识别动频中各阶固有振型的位置,如图10所示(以来流风速为9 m/s,转速550 r/min为例)。
通过对图10分析发现,在风轮动态振动频谱中轴向窜动和旋转基频的加速度幅值较高,并且发现在噪声频谱和振动频谱中旋转基频的频率保持良好一致性。因此,本文主要从风轮轴向窜动和旋转基频振动幅值进行分析,探究翼型凹变对风轮动频的影响。
其中,图10中识别风轮的各阶振型如表4所示。
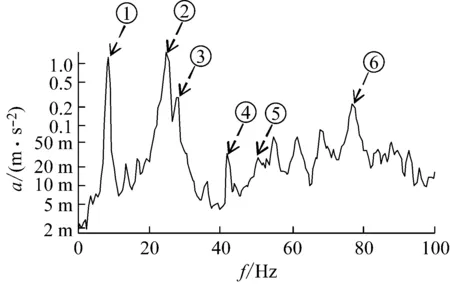
(a) A叶片
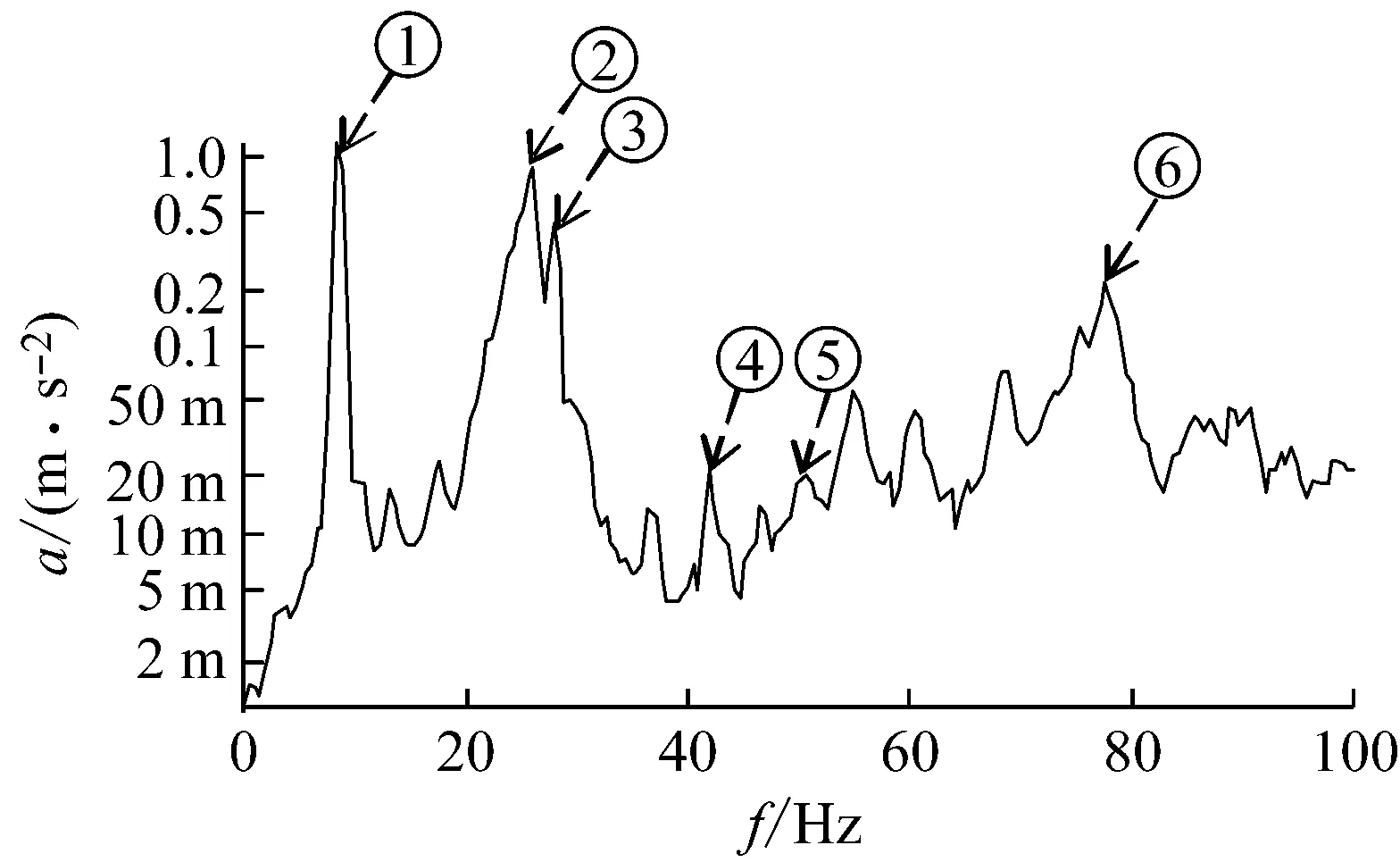
(b) B叶片

表4 振型参照表
2.2.3 对轴向窜动的影响分析
通过对轴向窜动随工况变化分布图(图11)分析发现,在相同工况下B叶片轴向窜动的加速度值普遍小于A叶片,说明翼型凹变后使叶片的动刚度得到提升,在受相同载荷力时可以有效减弱风轮在运行中沿轴向的振动强度。同时,当风速相同时,加速度值随着转速的增加呈现出先增加后减小的趋势,当转速达到550 r/min时,轴向加速度的值达到最大值。分析原因发现,当转速为550 r/min时,其旋转基频的频率与风轮一阶反对称的频率十分接近,导致叶片发生共振,因而导致叶片振动加速度值会出现陡增。随着风轮转速的增加,叶片由于离心钢化作用,其动刚度会进一步增加,进而造成加速度幅值逐渐减小。另外发现,当转速相同时,轴向窜动的加速度幅值随着风速的增加而逐渐增大。
2.2.4 对旋转基频振动的影响分析
通过对旋转基频振动随工况变化分布图(图12)分析发现,在相同工况下B叶片的旋转基频加速度幅值普遍小于A叶片,说明翼型凹变也可以有效减弱风轮旋转基频的振动强度。同时发现,旋转基频加速度的幅值随工况的变化趋势与轴向窜动相似,即随转速的增加呈现先升高后降低的趋势,并随风速的增加而逐渐增大。另外,旋转基频的振动加速度幅值要高于轴向窜动,且翼型凹变对旋转基频振动的影响较弱。
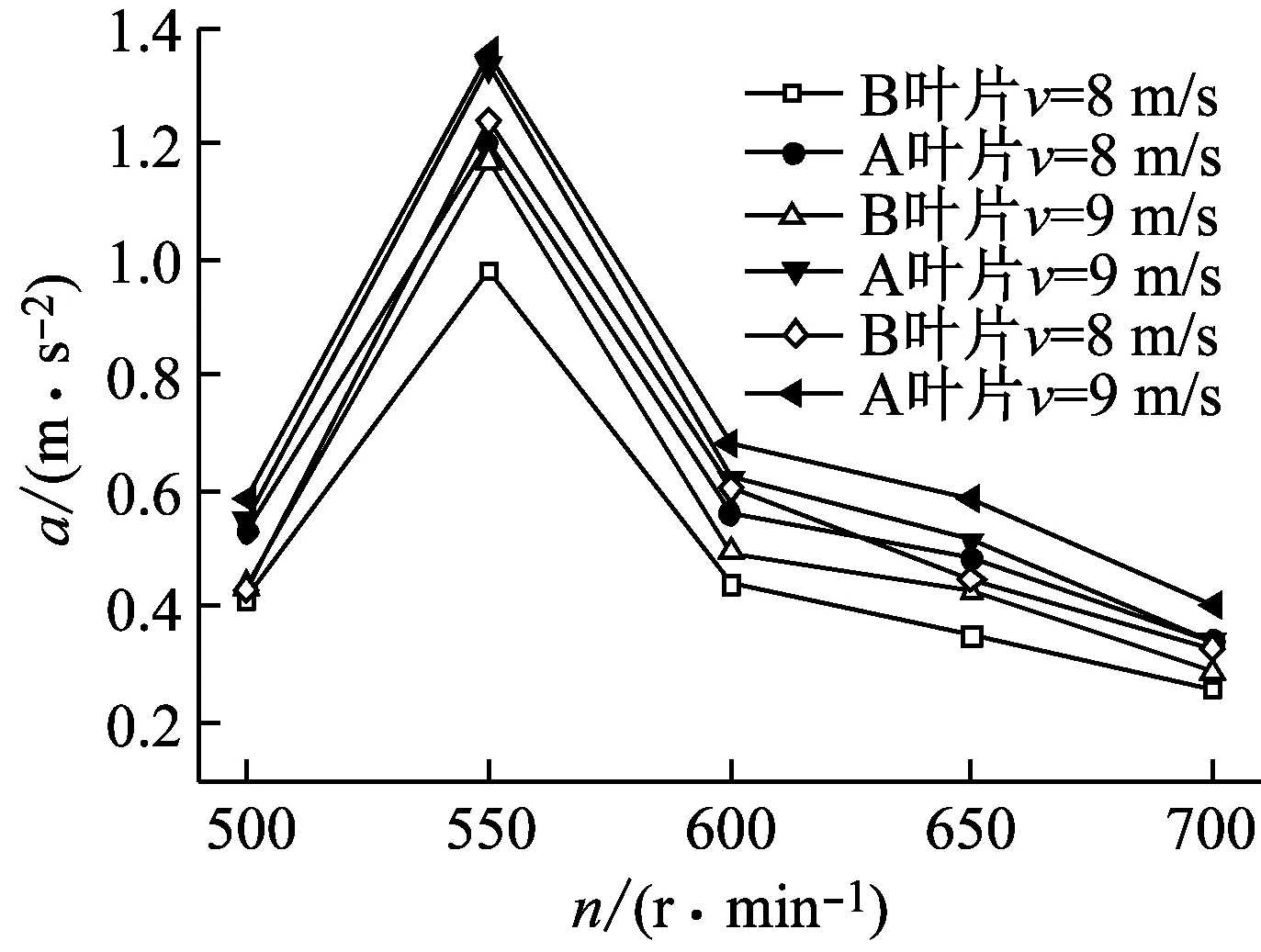
(a) 轴向窜动随转速的变化
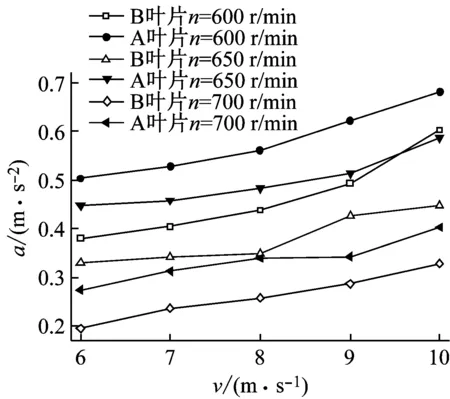
(b) 轴向窜动随风速的变化
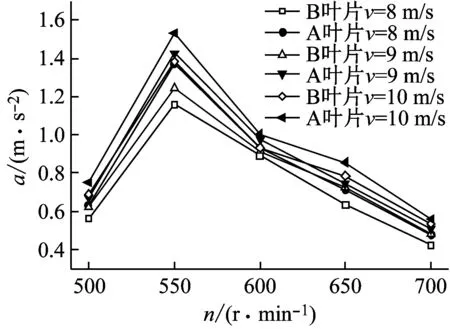
(a) 旋转基频振动随转速的变化
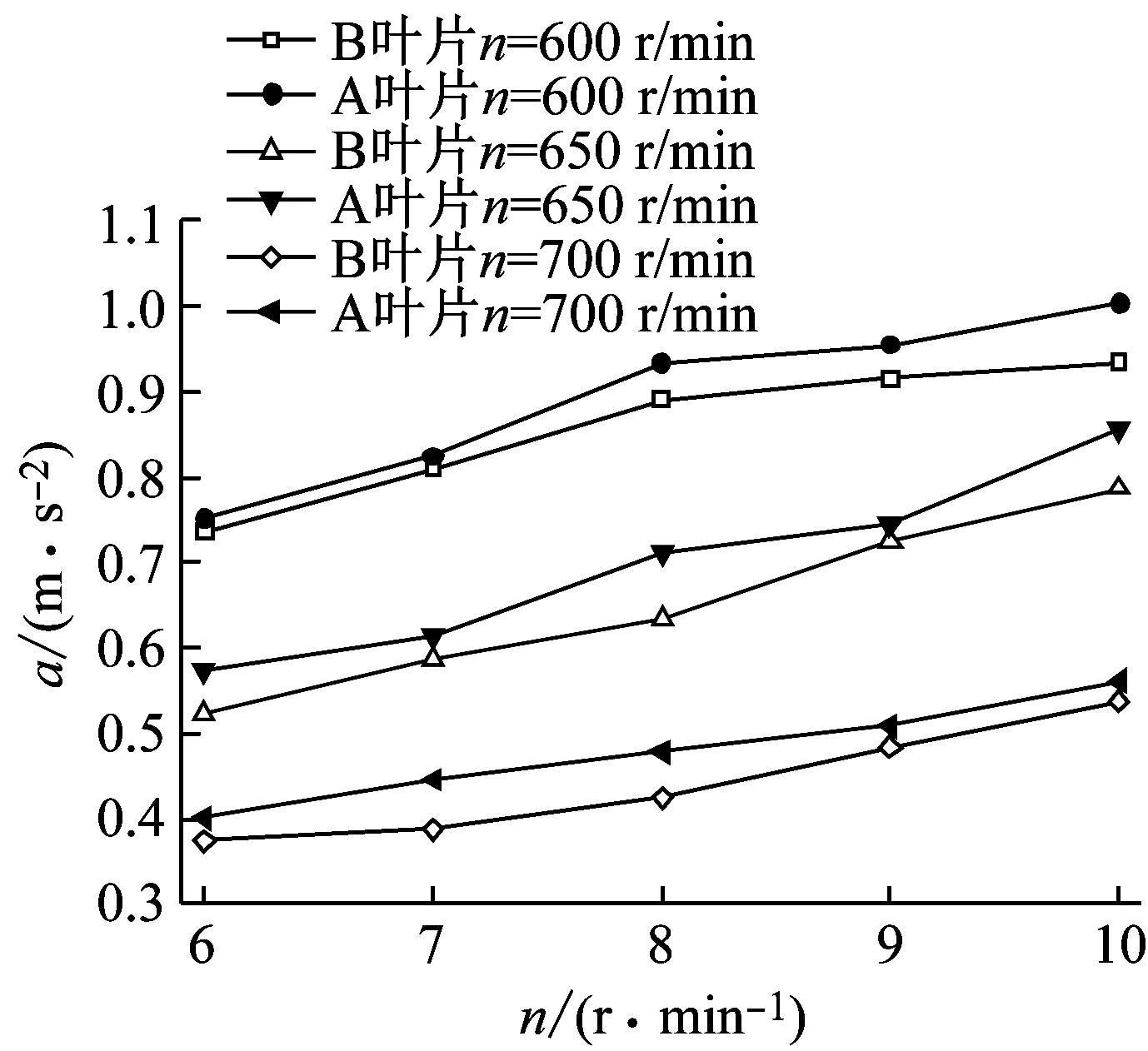
(b) 旋转基频振动随风速的变化
2.3 关联性分析
通过对风轮进行模态和动态测试发现,翼型凹变后对叶片刚度的提升,使风轮叶片在受到相同气动载荷时,风轮的轴向窜动和旋转基频振动的振动强度减弱,导致风轮对周围流体的压缩和膨胀作用减弱,从而起到降低旋转噪声的效果。
另外,通过以上频谱图发现叶片的旋转噪声和轴向窜动及旋转基频振动随工况的变化趋势保持良好的相似性。其中当风速相同时,旋转基频噪声的声压级随着转速呈现出先升高后降低的趋势,且其峰值出现在转速为550 r/min的工况,这是因为此刻出现共振现象,导致叶片的振动强度变大,加强了对周围流体的涨缩作用,从而引起噪声声压级的升高。随着转速的升高,叶片受离心钢化作用,进一步提升了叶片的刚度,从而逐步减弱了对周围流体的涨缩作用,导致声压级随转速的升高而逐渐降低。
3 结 论
本文主要对风轮叶片进行旋转噪声、模态和动频测试,探究了翼型凹变对风轮旋转噪声和结构特性的影响,同时,分析了风轮旋转噪声产生的原因以及叶片振动与噪声之间的关联性,并得出以下结论。
通过对叶片轴向窜动和旋转基频振动分析发现,在相同工况下,翼型凹变后对叶片刚度的提升,可以有效减弱叶片的振动强度。
通过对风轮旋转噪声分析发现,在相同工况下,翼型凹变后可以明显降低风轮的旋转噪声,且降噪效果随着旋转基频的倍频次数增加而逐渐增强。
通过对风轮旋转噪声产生原因分析发现,翼型凹变后对叶片刚度的提升,使风轮叶片在受到相同气动载荷时,风轮的振动强度减弱,导致风轮对周围流体的压缩和膨胀作用减弱,从而起到降低旋转噪声的效果。
